Economía
Relación de la contabilidad con la administración y la estadística
REPUBLICA BOLIVARIANA DE VENEZUELA
FUNDAUDO
CURSO DE ASISTENTE ADMINISTRATIVO PETROLERO
RELACION DE LA CONTABILIDAD CON LA ADMINISTRACIÓN Y LA ESTADÍSTICA
INDICE
DESCRIPICION PAG
Contabilidad 2
Administración 2
Estadística 2
Relación de la Contabilidad con la Administración y la Estadística 3
Contabilidad Administrativa 3
Métodos Estadísticos 4
Aplicación de la Estadística con la Administración y la Contabilidad 4 - 13
Conclusión 14
Bibliografía 15
INTRODUCCION
A continuación presentaremos la relación existente entre las tres disciplinas o ciencias básicas utilizadas en el planteamiento, desarrollo y resolución de eventos y proyecciones en la vida cotidiana. Dichas ciencias sirven de base al momento de establecer los resultados requeridos en un proyecto y área determinada, ya sean en lo económico, político o social.
La contabilidad provee las herramientas y los datos numéricos necesarios llevándolos a la ejecución estadística, esta a su vez se sirve de los procedimientos y principios básicos de la administración, para así obtener los resultados esperados en un lugar y tiempo determinado. De ahí la importancia que radica en el trabajo conjunto de estas tres ciencias, ya que, en todo plan, proyecto, etc., se requiere de procedimientos y técnicas para la ejecución, elaboración y resultados.
DESARROLLO
Para conocer la relación que existe entre la Contabilidad con la Administración y la Estadística debemos conocer sus significados:
CONTABILIDAD
Técnicas que se utiliza para producir sistemática y estructuralmente información cuantitativa expresada en unidades monetarias de las transacciones que realiza una entidad económica y de ciertos eventos económicos identificables y cuantificables que la afectan, con el objetivo de facilitar a los interesados la toma de decisiones en relación con dicha entidad económica, a su vez es un soporte básico para tomar decisiones sobre inversiones, basándose en criterios y procedimientos existentes para asegurar la correcta valoración de bienes, derechos y obligaciones.
ADMINISTRACION
Consiste en planificar, organizar, dirigir controlar el trabajo de los miembros de una organización haciendo uso de los recursos disponibles para alcanzar las metas o los objetivos establecidos.
ESTADÍSTICA
Es una rama de las matemáticas que se ocupa de reunir, organizar y analizar datos numéricos y que ayuda a resolver problemas como el diseño de experimentos y la toma de decisiones, tiene como finalidad facilitar la solución de problemas en los cuales necesitamos conocer algunas características sobre el comportamiento de algún suceso o evento. Características que nos permiten conocer o mejorar el conocimiento de ese suceso. Además nos permiten inferir el comportamiento de sucesos iguales o similares sin que estos ocurran. Esto nos da la posibilidad de tomar decisiones acertadas y a tiempo, así como realizar proyecciones del comportamiento de algún suceso. Esto es debido a que solo realizamos los cálculos y el análisis con los datos obtenidos de una muestra.
RELACION DE LA CONTABILIDAD CON LA ADMINISTRACION Y LA ESTADÍSTICA
La Estadística, como ciencia analiza hechos yendo desde los más pequeños hasta los más grandes y a la inversa. Sin embargo de nada le servirían los métodos que aplican si careciera de la información adecuada y esta en buena medida le será brindada por la Contabilidad, por medio de los registros individuales y de conjuntos. La Contabilidad también recurre a los métodos estadísticos para establecer los hechos futuros, en especial la Administración por lo que ambas se complementan con mucha frecuencia y buenos resultados. Mientras una proporciona elementos para que construya con sus métodos los resultados de los datos obtenidos la otra le proporciona las tendencias o las posibilidades para que proyecte el futuro.
La contabilidad a su vez tiene una rama que tiene como herramienta principal La Estadística, esta rama es la Contabilidad Administrativa, cuyo concepto es:
Contabilidad Administrativa:
Sistema de información al servicio de las necesidades de la administración, con orientación pragmática destinada a facilitar las funciones de planeación, control, y toma de decisiones.
La Contabilidad Administrativa, como sistema de información administrativa, recurre a disciplinas como La Estadística, la economía, la investigación de operaciones, las finanzas, etc., para completar los datos presentados con el fin de aportar soluciones a los problemas de la organización.
La Contabilidad Administrativa hace hincapié en las áreas de la empresa como células o centros de información (como divisiones, líneas de producción, etc.) para tomar decisiones sobre cada una de las partes que la componen, más que toda la empresa vista globalmente, tarea que tiene a su cargo la contabilidad financiera al informar sobre los sucesos ocurridos en la empresa.
METODOS ESTADISTICOS
La materia prima de la ESTADISTICA consiste en conjuntos de números obtenidos al contar o medir cosas. Al recopilar datos estadísticos se ha de tener especial cuidado para garantizar que la información sea completa y correcta.
El primer problema para los estadísticos reside en determinar qué información y cuánta se ha de reunir. Para establecer una ley física, biológica o social, el estadístico debe comenzar con un conjunto de datos y modificarlo basándose en la experiencia.
En nuestros días, la estadística se ha convertido en un método efectivo para describir con exactitud los valores de los datos económicos, políticos, sociales, psicológicos, biológicos y físicos, y sirve como herramienta para relacionar y analizar dichos datos. El trabajo del experto estadístico no consiste ya sólo en reunir y tabular los datos, sino sobre todo el proceso de interpretación de esa información. El desarrollo de la teoría de la probabilidad ha aumentado el alcance de las aplicaciones de la estadística. Muchos conjuntos de datos se pueden aproximar, con gran exactitud, utilizando determinadas distribuciones probabilísticas; Los resultados de éstas se pueden utilizar para analizar datos estadísticos. La probabilidad es útil para comprobar la fiabilidad de las infererencias estadísticas y para predecir el tipo y la cantidad de datos necesarios en un determinado estudio estadístico.
EJEMPLO DE LA APLICACION DE LA ESTADISTICA CON LA ADMINISTRACIÓN Y LA CONTABILIDAD.
Describiremos la aplicación de Estadística, con las ideas expuestas con un caso práctico de la vida real, el cual se presenta con muchísima frecuencia:
Un estudiante que toma un curso en la escuela, siempre le interesa saber con anticipación como será su resultado al finalizar el curso. Que oportunidad tiene de aprobar el curso y con que calificación, lo cual no es posible determinar con certeza hasta finalizar el curso.
Pero con el uso de la estadística puede conocer de forma aproximada esta información. Él puede tomar las calificaciones (que son los datos) de todos los cursos anteriores y hacer un promedio (que seria la media aritmética). Así tendría una idea de cuales son en general los resultados que se obtienen en ese curso. También puede obtener un porcentaje de cuántos estudiantes obtienen una determinada calificación.
Lo que luego le permitiría de acuerdo al número total de estudiantes en ese curso determinar cual sería su probabilidad de obtener una determinada calificación. También puede obtener un porcentaje de las personas que aprueban o no el curso y así conocer su oportunidad, de igual forma de acuerdo al total de alumnos del curso obtener su probabilidad de aprobar o no el curso.
Pero este trabajo que necesita hacer con los datos de todas las calificaciones anteriores de ese curso, llevaría muchísimo tiempo y trabajo. Es muy posible que cuando tenga los resultados ya no le sirvan, pues ha terminado el curso y ya conoce con certeza sus calificaciones. Es allí donde tiene un papel importante la estadística.
De todas las calificaciones anteriores, que seria la población, solo se toman algunas, esto seria una muestra. Para seleccionar la muestra existen varias maneras de hacerlo o métodos. Como por ejemplo: tomar solo las del último curso. Tomar cinco calificaciones de cada curso. Tomar cinco calificaciones de los últimos diez cursos, dejando a la suerte cuales serian las cinco calificaciones a tomar. Esto sería selección aleatoria, también se podría tomar algunos cursos al azar o aleatoriamente y de ellos algunas calificaciones también aleatoriamente.
Un aspecto importante es el tamaño de la muestra. Este está relacionado directamente con la precisión de los resultados que se obtendrán. Cuanto mayor sea el tamaño de la muestra mayor precisión tendrán los resultados, pues el tamaño de la muestra estará mas cerca del tamaño de la población y cuanto más pequeña sea el tamaño de la muestra, estará mas lejos del tamaño de la población por lo que los resultados serán menos precisos. Por tal motivo existen métodos para poder establecer o calcular de acuerdo a la situación cuál es el tamaño de la muestra adecuado. Esto no quiere decir que no pueda seleccionarse otro tamaño de la muestra, solo es más recomendable.
Otro aspecto importante podría ser dividir el grupo de estudiantes en cuatro categorías: A, B, C y D. Pues supongamos se asignan tres tipos de becas a los estudiantes, de la siguiente forma. Al 25% que saque mayores notas (categoría A) se le da una beca por 5 años. Al 25% que le sigue en calificaciones (categoría B) se le otorga una beca por 3 años. Al 25% siguiente (categoría C) una beca por 1 año y al 25% restante (categoría D) no se le otorga ninguna beca.
Esto quiere decir por ejemplo que en una clase de 20 estudiantes que estén ordenados por calificaciones en orden descendente: del 1 al 5 se becan por 5 años, del 6 al 10 se becan por 3 años, del 11 al 15 se becan por 1 año, y del 16 al 20 no reciben beca.
Si quisiéramos conocer que oportunidad tenemos de obtener una beca. Podríamos tomar un grupo de notas o datos, de forma aleatoria entre todas las notas de los cursos dictados anteriormente o población. Esto representaría una muestra. Luego determinamos cuales son las calificaciones que establecen a que categoría pertenece el estudiante.
Esto es equivalente a calcular los cuartiles: primer cuartil, segundo cuartil y tercer cuartil. Que no es otra cosa que los valores correspondientes a la escala de calificaciones, en las cuales se producen los cambios para cada categoría.
Es decir el tercer cuartil representa la calificación a partir de la cuál están ubicados el 25% de los estudiantes de categoría A, el segundo cuartil (igual a la mediana) es igual a la calificación en la cual hay 50 % de los estudiantes por encima y 50% por debajo, los que están entre el segundo y el tercer cuartil son el 25% de estudiantes categoría B. Y el primer cuartil es representa la calificación por debajo de la cual hay 25% de estudiantes categoría D, además los que están entre el primer cuartil y el segundo son el 25% categoría C.
Esto puede de una forma más sencilla permitirle también tener una buena idea de que oportunidad tiene de obtener una determinada beca dentro de este curso.
Pero además de esto también es importante conocer la regularidad o normalidad de las calificaciones en los cursos anteriores, esto quiere decir saber si se mantiene o no el mismo comportamiento en todos los cursos. Lo cual es importante para saber si los resultados obtenidos del análisis tienen validez o no. Esto es posible hacerlo calculando la Correlación entre las notas de los cursos.
Para ilustrar con más detalles la idea presentada, vamos a resolver un ejemplo con un caso similar. Así veremos como aplicar cada una de las ideas mencionadas anteriormente, además veremos como se hacen los respectivos cálculos.
Tenemos un curso de Estadísticas que se ha dictado 10 veces anteriormente, las calificaciones obtenidas por los estudiantes de esos cursos se muestran en la tabla # 1.
| Tabla # 1
|
Lo primero que se tiene que hacer es organizar los datos mediante una Tabla de distribución de frecuencias(tabla # 2). Los datos recogidos deben ser organizados, tabulados y presentados para que su análisis e interpretación sean rápidos y útiles.
Por ejemplo, para estudiar e interpretar la distribución de las notas o calificaciones de un examen en una clase con 28 alumnos, primero se ordenan las notas en orden creciente: 3,0; 3,5; 5,2; 6,1; 6,5; 6,8; 7,0; 7,2; 7,2; 7,3; 7,5; 7,5; 7,6; 7,7; 7,8; 7,8; 8,0; 8,3; 8,5; 8,8; 9,0; 9,1; 9,6; 9,1; 9,6; 9,7; 10 y 10. Esta secuencia muestra, a primera vista, que la máxima nota es un diez, y la mínima es un 3; el rango, diferencia entre la máxima y la mínima es 7.
Gráfico # 1 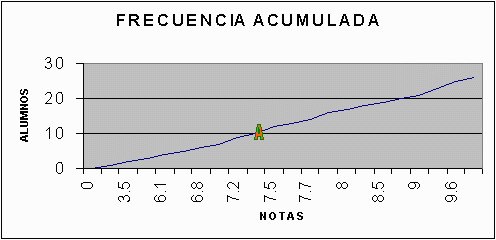
En un diagrama de frecuencia acumulada, como en gráfico # 1, las notas aparecen en el eje horizontal y el número de alumnos en el eje vertical izquierdo, con el correspondiente porcentaje a la derecha. Cada uno representa el número total de estudiantes que han obtenido una calificación menor o igual que el valor dado. Por ejemplo, el punto A corresponde a 7,4, y según el eje vertical, hay diez alumnos, o un 38%, con calificaciones menores o iguales que 7,4.
Para analizar las calificaciones obtenidas por 10 cursos de 17 alumnos cada uno tenemos un total de 170 calificaciones, hay que tener en cuenta que la cantidad de datos es demasiado grande para representarlos como en el gráfico # 1. El estadístico tiene que separar los datos en grupos elegidos previamente denominados intervalos.
Por ejemplo, se pueden utilizar 10 intervalos para tabular las 170 calificaciones, que se muestran en las columnas de la tabla # 1 de distribución de datos; el número de calificaciones por cada intervalo, llamado frecuencia del intervalo, se muestra en la tabla # 2. Los números que definen el rango de un intervalo se denominan límites. Es conveniente elegir los límites de manera que los rangos de todos los intervalos sean iguales y que los puntos medios sean números sencillos.
Una calificación de 87 se encuentra en el intervalo entre 81 y 90; una calificación igual a un límite de intervalo, como 90, se puede asignar a cualquiera de los dos intervalos, aunque se debe hacer de la misma manera a lo largo de toda la muestra. La frecuencia relativa y La frecuencia acumulada, son indispensables en la construcción de la tabla de frecuencias y para facilitar el cálculo. Así, el número de estudiantes con calificaciones menores o iguales a 30 se calcula sumando las frecuencias de la columna (d) de los tres primeros intervalos, dando 6.
| Tabla # 2
|
Un histograma o diagrama de barras (como en el gráfico 2), o como un polígono de frecuencias (como en el gráfico 3), nos permiten un análisis más rápido de los datos.
De la tabla # 2, o de los gráficos #1 y #2 podemos observar por ejemplo, que si el curso se aprueba con 50 ptos. Solo hay 21 estudiantes con notas por debajo de 50, por lo cual hay 149 estudiantes con calificaciones sobre 50 puntos.
Por lo tanto 149/170 = 0.88 es la probabilidad que tengo de aprobar el curso y 0.12 es la probabilidad que tengo de reprobar el curso. Por otra parte si se aprobara el curso con 60 ptos. Serían 55 alumnos por debajo de 60 y 115 alumnos sobre 60 ptos. Lo que nos daría una probabilidad de aprobar de 115/170 = 0.68 o 68% de posibilidades de aprobar el curso y una probabilidad de reprobar el curso de 0.32 o un 32% de posibilidades de reprobar el curso.
Gráfico # 2 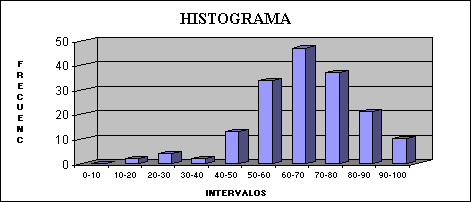
Gráfico # 3 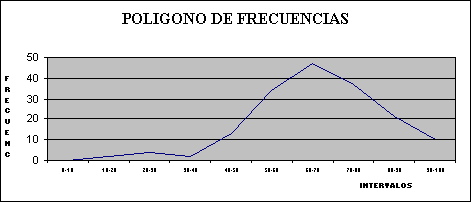
Luego calculamos algunas medidas de tendencia central y algunas medidas de dispersión:
La media aritmética de la siguiente forma: se suman todas las notas de los diez cursos y obtenemos 11350, luego dividimos entre el número de notas que es 170. Y obtenemos una media de 66.76. Lo que quiere decir que la nota promedio de todos los cursos de estadística es 67 puntos.
| _ |
La Mediana de la siguiente forma:
Mediana=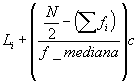
Donde:
Li= frontera inferior de la clase de la mediana.
N= número de datos (frecuencia total).
![]()
= suma de frecuencia de las clases inferiores a la de la mediana
fmediana= frecuencia de la clase de la mediana
c= anchura del intervalo de la clase de la mediana.
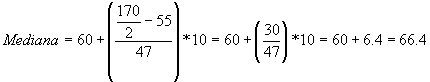
Esto nos quiere decir que hay 50% de las notas sobre 66.4 y el otro 50% esta por debajo. En otras palabras de los 170 estudiantes, 85 han obtenido una calificación por encima de 66.4 puntos.
El Primer Cuartil: se calcula de igual forma que la mediana, solo que el número de datos se divide entre 4, solo se toman la cuarta parte de los datos o el 25% de los datos y la frontera inferior corresponde a la del cuartil.
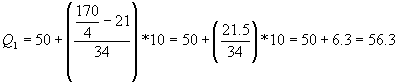
Esto nos dice que hay un 25% de las notas por debajo de 56.3 puntos, o bien aproximadamente 42 estudiantes de los 170 han sacado una calificación inferior a 56.3 puntos.
El Tercer Cuartil: se calcula de igual forma que la mediana, solo que el número de datos multiplica por tres y se divide entre 4, solo se toman las tres cuartas partes de los datos o el 75% de los datos.
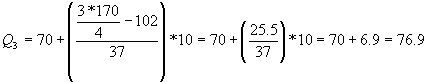
Esto nos dice que hay un 25% de las notas sobre 76.9 puntos, o bien aproximadamente 42 estudiantes de los 170 han sacado una calificación sobre 76.9 puntos.
La Moda de la forma siguiente:
La moda es el valor que más se repite, en este caso tenemos que hay tres modas: las notas 58, 63 y 68 se repiten siete veces cada una.
La Desviación Típica de la forma siguiente:
![]()


Si restamos y sumamos la desviación típica a la media tenemos el rango de notas en el que se encuentra el 95% de los estudiantes.
| _ |
Entonces tenemos que el 95% de los estudiantes, aproximadamente 162 estudiantes, tienen notas entre 51 y 83 puntos. Si la desviación típica es pequeña, los datos están agrupados cerca de la media; si es grande, están muy dispersos.
Por otro lado tenemos con respecto a las becas, que para obtener una beca tipo A por 5 años en promedio hay que obtener mas de 77 puntos que es el valor del Tercer Cuartil, para obtener una beca tipo B por tres años, hay que obtener una nota promedio sobre 67 puntos que es la Media Aritmética o Segundo Cuartil, para obtener una beca tipo C por un año, hay que obtener una nota promedio sobre 56 puntos, que es el valor del Primer Cuartil, y si se obtiene una calificación inferior a 56 puntos no se obtiene ninguna beca.
Supongamos ahora que nos inscribimos en un curso de estadística que tiene 20 estudiantes y queremos saber que oportunidad de obtener una beca de cualquier tipo tenemos. Entonces debemos calcular la probabilidad de estar en la cuarta parte del grupo de 20 estudiantes.
La Probabilidad esta definida como:
![]()
Casos favorables: son el 75% de 20 estudiantes, es decir 15 estudiantes.
Casos posibles: es el 100% de los estudiantes, es decir 20 estudiantes.
Probabilidad de Obtener una beca de cualquier tipo:
![]()
De forma similar obtenemos:
|
|
|
|
|
|
Pero no siempre es fácil manipular o poder obtener todos los datos, entonces es necesario tomar muestras, vamos a tomar dos muestras por diferentes métodos, para mostrar como puede hacerse, además de mostrar que sencillos serían los cálculos con una muestra.
Muestra A: para la muestra a podemos colocar diez bolitas numeradas del 1 al 10 en una bolsa, luego sin observar sacar una bolita por ejemplo la #7, esto sería que hemos tomado las notas del curso #7 para hacer los cálculos. Según la tabla #7 tenemos:
Muestra: 84,30,63,58,80,72,56,65,77,78,65,68,77,56,78,67 y 76.
Muestra B: para la muestra A podemos colocar 17 bolitas numeradas del 1 al 17 en una bolsa, luego sin observar sacar dos bolitas que serían las dos notas que tomaría del curso 1, por ejemplo la #5 y la #13, que serian las notas 73 y 59 de la tabla #1. Esto sería que hemos tomado las notas del curso #7 para hacer los cálculos. Y repetir éste proceso hasta completar dos notas de cada curso, con lo que tendríamos 20 notas que formarían la Muestra B.
Luego si calculamos la media aritmética y la desviación típica para la muestra A, tenemos:
|
|
|
De lo cual podemos observar como la media calculada con las notas de todos los estudiantes o Población que es 66.7 ptos. Está muy cerca de la media calculada con la muestra que es 67.7. De igual forma observamos cómo los valores de las desviaciones típicas son cercanos. Siempre que la muestra sea tomada de una forma adecuada y de un tamaño representativo de la población los resultados obtenidos serán muy parecidos, como los obtenidos aquí.
Si la muestra es pequeña, no es necesario agrupar los datos en una tabla de frecuencia, por lo tanto.
De esta forma esperamos haber contribuido al conocimiento y uso de la Estadística, para aquellas personas que no tenían conocimientos sobre esta ciencia tan necesaria y usada con mayor frecuencia cada día.
CONCLUSION
La contabilidad es un soporte básico para tomar decisiones sobre inversiones, basándose en criterios y procedimientos existentes para asegurar la correcta valoración de bienes, derechos y obligaciones.
La contabilidad administrativa está organizada para producir información de uso interno de la administración. La labor de administrar una organización requiere por parte de su responsable, una serie de datos que no son los mismos que se pretende presentar a los interesados externos relacionados con la organización, como los accionistas, las instituciones de crédito, etc. Ello obliga a tomar decisiones de todo tipo. La diferencia básica radica en la forma como se presenta la información hacia el exterior, que defiere de la requerida para usos internos.
La Estadística, además de ser una rama de las matemáticas que se ocupa de reunir, organizar y analizar datos numéricos y que ayuda a resolver problemas como el diseño de experimentos y la toma de decisiones, tiene aplicación en cualquier campo, sin importar que tan sencillo o complicado sea. Cuanto más complicado sea, más ayuda nos presta para resolver la situación; la estadística se ha convertido en un método efectivo para describir con exactitud los valores de los datos económicos, políticos, sociales, psicológicos, biológicos y físicos, y sirve como herramienta para relacionar y analizar dichos datos.
BIBLIOGRAFIA
Valdes, Fernando, COMPRESIÓN Y USO DE LA ESTADISTICA, Universidad Rómulo Gallegos, España
Hernández Rodríguez, Sergio INTRODUCCIÓN A LA ADMINISTRACIÓN. México, 1994.
Gómez, Giovanni E. EVALUACION Y ESTIMACION ESTADISTICA DE PROYECTOS FINANCIEROS, www.gestiopolis.com
UNIVERSIDAD NACIONAL AUTONOMA DE MEXICO FACULTAD DE CONTADURIA Y ADMINISTRACION
Descargar
| Enviado por: | Eliana |
| Idioma: | castellano |
| País: | Venezuela |