Matemáticas
Matemáticas
ÍNDEX 2-3
1. MATRIUS 4-6
1.1. Tipus de matrius
1.1.1. Segons la forma
1.1.2. Segons els elements
1.2. Operacions amb matrius
1.2.1. Suma i resta
1.2.2. Producte de matrius per un nombre
1.2.3. Producte de matrius
1.3. Matriu inversa
2. DETERMINANTS 7-8
2.1. De tercer ordre
2.2. L'adjunt d'un element
2.3. Càlcul de la matriu inversa per mitja de determinants
2.4. Matrius amb paràmetres: matriu inversa
3. SISTEMES D'EQUACIONS LINEALS 9-12
3.1. En general
3.2. Teorema de Rouché
3.3. Mètode de Gauss
3.3.1. Sistema de dues equacions
3.3.2. Sistema de tres equacions
3.4. Mètode de Cramer
3.5. Resolució de sistemes per la matriu inversa
4. VECTORS 13-15
4.1. Conceptes bàsics
4.2. Producte escalar
4.3. Producte vectorial
4.4. Producte mixt
5. EQUACIÓ DE LA RECTA I EL PLA 16-17
5.1. Punts coplanaris i colineals
5.2. Equacions de la recta
5.2.1. Equació vectorial
5.2.2. Equació paramètrica
5.2.3. Equació contínua
5.2.4. Equació de la recta que passa per dos punts
5.3. Equacions del pla
1. MATRIUS
En matemàtiques anomenem matriu tant a les llistes com a les taules d'elements. Fixem-nos en la matriu següent:
Si ens fixem, cada element té com a subíndex. El primer dels nombre indica la fila en què ens trobem (el valor màxim està indicat com a m) mentre que el segon estableix la columna (i el nombre màxim és n).
El nombre de files i columnes d'una matriu s'anomena dimensió, i es designa per m·n. En el cas que el nombre m sigui igual a n, la matriu serà quadrada i l'anomenarem matriu d'ordre n.
1.1. Tipus de matrius
1.1.1. Segons la forma
-
Matriu filera: és aquella que només té una filera, per exemple
-
Matriu columna: només té una columna. Exemple:
-
Matriu quadrada: té el mateix nombre de files i de columnes. Un exemple seria la següent:
-
Matriu rectangular: la matriu tindrà forma de rectangle. Exemple:
-
Matriu transposada: és aquella que s'obté canviant les files per les columnes. Si la primera matriu té una dimensió m·n, després en tindrà
n· m. Fixem-nos:
-
Matriu simètrica: la coneixem com aquella en que els elements són iguals. Veiem-ho:
-
Matriu antisimètrica: igual que l'anterior, però ara un dels nombres serà de signe contrari.
1.1.2. Segons els elements
-
Matriu nul·la (o zero): tots els seus elements valen 0.
-
Matriu diagonal: únicament els nombres són diferents a 0 a la diagonal principal.
-
Matriu escalar: igual que l'anterior, però tots els nombres de la diagonal són els mateixos.
-
Matriu identitat (o unitat): igual que l'anterior, però a la diagonal només hi ha el número 1.
-
Matriu triangular: matriu quadrada en que tots els termes que es troben per sota (o per sobre) de la diagonal són nuls.
triangular superior triangular inferior
1.2. Operacions amb matrius
1.2.1. Suma i resta
Tant la resta com la suma de matrius (de la mateixa dimensió) es realitza component a component. Veiem-ho amb el següents exemples.
SUMA
RESTA
1.2.2. Producte de matrius per un nombre
Es realitza multiplicant cada el nombre per cada component
Tot i que la matriu fos d'una dimensió superior, el procediment seria el mateix.
1.2.3. Producte de matrius
Per tal de multiplicar matrius, hem de fixar-nos que el nº de columnes de la primera sigui igual al de files de la segona. Per operar i trobar, per posar un cas, l'element , haurem de multiplicar tota la segona fila de la primera matriu per tota la tercera columna de la segona. Exemple:
| 1 | 2 | 3 | · | 1 | 2 | -1 | 5 | = | 10 | 6 | 15 | 29 |
| -1 | 5 | 0 | 0 | -1 | 2 | 3 | -1 | -7 | 11 | 10 |
| 2 | 1 | 2 | 3 | 2 | 4 | 6 | 8 | 7 | 8 | 25 |
1.3. Matriu inversa
Calculem la inversa de . Hem de trobar una matriu .
·=
2. DETERMINANTS
2.1. De tercer ordre
Per tal de calcular el valor d'un determinant 3x3 hem d'utilitzar la regla de Sarrus, consistent a multiplicar i sumar els productes per després multiplicar i restar, tal i com s'indica al següent exemple:
2.2. L'adjunt d'un element
Es designa com adjunt d'un element al determinant que resta en eliminar la fila i columna on es troba aquest. El mètode dels adjunts és una altra manera de trobar el valor d'un determinant.
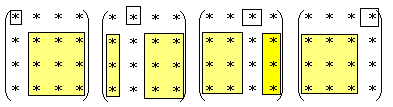
Una de les seves característiques es que cada nombre té un signe assignat:
Fixem-nos-hi en el següent esquema, on el quadrat pintat indica el determinant del nombre que volem saber (el quadrat sense pintar).
2.3. Càlcul de la matriu inversa per mitja de determinants
Donada una matriu quadrada A, s'anomena matriu adjunta de A, i es representa per Adj A, la matriu que s'obté en substituir cada element pel seu adjunt. Exemple:
Els adjunts de cada element són: i la matriu adjunta:
A continuació trobem la transposada i la multipliquem per la matriu A
Resumint, per trobar la matriu inversa hem d'aplicar la fórmula següent:
2.4. Matrius amb paràmetres: matriu inversa
Imaginem que tenim la següent matriu i ens demanen:
Calcula m de manera que la matriu A no tingui inversa.
El primer que hem de fer és calcular el determinant de la matriu: det A= -1
Si el determinant de la matriu fos 0, això voldria dir que m-1=0, d'on podem extreure que la matriu no té inversa quan m=1.
Per a tota la resta de casos existirà inversa, ja que el determinant de la matriu serà diferent de 0.
3. SISTEMES D'EQUACIONS LINEALS
3.1. En general
Una solució del sistema és un conjunt ordenat de nombres reals de manera que en substituir les incògnites , etc. les matrius se satisfan alhora.
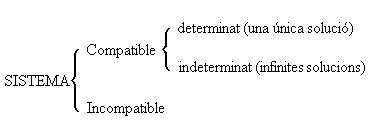
Podem classificar els sistemes de la següent manera:
Matriu del sistema
Matriu ampliada del sistema
3.2. Teorema de Rouché
El teorema de Rouché ens diu que un sistema és compatible si el rang de la matriu dels coeficients de les incògnites és igual al rang de la matriu ampliada amb la columna dels termes independents.
Dins el teorema de Rouché podem tenir els següents tipus de sistemes:
-
S.C.D.
-
S.C.I.
-
S.I.
Exemple: Estudia la compatibilitat i el nombre de solucions del següent sistema
Rang M=2, ja que la columna és igual a i les dues primeres columnes són proporcionals.
Rang M*=3, ja que
Per tant es tracta d'un sistema incompatible (S.I.), ja que
3.3. Mètode de Gauss
3.3.1. Sistema de dues equacions
Ens centrarem en el mètode de reducció - substitució, i per aprendre'n ens fixarem en el següent exemple.
Multipliquem la 1a equació per 2, deixem la segona com estava i sumem.
D'on podem concloure que: x=8. Ara només cal substituir x a l'equació principal per extreure el valor d'y.
Solucions: x=8, y=9
3.3.2. Sistema de tres equacions
Els sistema de tres equacions de Gauss consisteix a fer zeros a la matriu per tal de trobar les incògnites. Fixem-nos en el següent exemple:
D'aquesta última matriu podem extreure que . A partir d'aquesta incògnita desvelada podem saber les altres dues:
S.C.D. Solucions (1,1,1)
3.4. Mètode de Cramer
Un sistema d'equacions lineals és un sistema de Cramer si compleix:
-
Té n equacions i n incògnites.
-
El determinant de la matriu de coeficients del sistema és diferent a zero.
-
És un Sistema Compatible (S.C.)
Per tal de trobar les incògnites hem de seguir els passos que es poden apreciar a l'exemple següent:
3.5. Resolució de sistemes per la matriu inversa
Si una matriu A és regular, hi ha d'haver alguna manera de trobar-ne la seva inversa. La fórmula per esbrinar-la és la següent:
Comprovem-ho amb el següent exercici resolt:
;
Per tant,
4. VECTORS
4.1. Conceptes bàsics
-
Combinació lineal de vectors: un vector u de V és combinació lineal dels vectors de V, si pot expressar-se així:
sent números reals.
Exemple: expressa (3,4,5) com combinació lineal dels vectors (1,0,0), (0,1,0) i (0,0,1)
-
Dependència o independència lineal de vectors: un conjunt de vectors és linealment dependent si un qualsevol d'ells es pot expressar com combinació lineal dels restants. En cas contrari són linealment independents.
-
Dependents:
-
Independents:
-
Generador: si un conjunt de vectors són linealment independents i a més combinació lineal, diem que són generadors
-
Vector fix: és un segment orientat que té l'origen en el punt A i l'extrem en el punt B. En podem conèixer el mòdul, la direcció i el sentit.
-
Vector lliure: és cada una de les classes en què queda classificat el conjunt mitjançant la relació d'equipol·lència.
-
Suma i resta de vectors: és sumen (o es resten) els components d'un vectors amb els de l'altre.
-
Producte d'un nombre real per un vector: es multiplica cada component del vector pel nombre desitjat. Exemple:
-
Perímetre: Suma de les (fer-ne el mòdul)
-
Punt mig:
4.2. Producte escalar
El producte escalar de dos vectors es designa per ![]()
·![]()
i s'obté de la manera següent:
Exemple: Quin és el producte escalar dels vectors (3,2,1) i (1,2,3)? Són perpendiculars?
Producte escalar
. No són .
4.3. Producte vectorial
El producte vectorial de dos vectors lliures de , és un altre vector que es designa per , i que s'obté de la manera següent:
Si són dos vectors no nuls i no proporcionals, és un vector que té:
Mòdul:
Direcció: perpendicular als vectors
Sentit: el sentit d'avançament d'un llevataps que gira en sentit positiu de
.
Si
El producte vectorial és emprat, entre altres coses, en el càlcul d'àrees. Fixem-nos-hi:
Tenim els vector
4.4. Producte mixt
El producte mixt de tres vectors lliures de l'espai és un nombre real que es designa per i que s'obté de la manera següent:
El producte mixt servei, per posar un cas, pel càlcul de volums de tetràedres o paral·lelepípedes. Veiem-ho amb l'exemple següent:
Donats els punts calcula el volum del tetràedre (piràmide de base triangular).
5. EQUACIÓ DE LA RECTA I EL PLA
5.1. Punts coplanaris i colineals
són colineals
són coplanaris
5.2. Equacions de la recta
* Formes per identificar una recta:
Dos punts
Un punt i un vector director
5.2.1. Equació vectorial
![]()
5.2.2. Equació paramètrica
S'aconsegueix igualant component a component a l'expressió vectorial.
5.2.3. Equació contínua
La podem trobar buscant el valor de a les tres equacions, i igualant els valors obtinguts.
A continuació, a mode d'exemple, obtindrem les tres equacions de la recta a partir del punt i el vector director
Equació vectorial
Equació paramètrica
Equació contínua
5.2.4. Equació de la recta que passa per dos punts
Per esbrinar-la hem d'utilitzar la fórmula:
5.3. Equacions del pla
* Formes per determinar un pla
Un punt i dos vectors directors
3 punts
Un punt i un vector normal
Una recta i un punt exterior
Temari d'ampliació de matemàtiques
2
Descargar
| Enviado por: | Javi |
| Idioma: | catalán |
| País: | España |
