Física
Estudio de la trayectoria en un medio viscoso
Estudio de la trayectoria en un medio viscoso
Descripción de los elementos utilizados:
1. Manguera plástica con aceite de automóviles en su interior sin burbujas de aire visibles; una pequeña elipse (ruleman) se desplazaba dificultosamente por el líquido.
2. Papel milimetrado (para marcar la trayectoria del ruleman)
Cronómetro digital (de acción manual)
Regla milimetrada
Realización de la práctica:
Colocamos la manguera sobre la hoja milimetrada (previamente fijada a una superficie rígida). Luego fijamos la manguera plástica de forma tal que describiese una trayectoria curva que creímos la más conveniente para realizar el estudio del movimiento. Una vez fijada la hoja y la manguera, procedimos a la medición de los tiempos mediante el uso de un cronómetro digital tomando intervalos regulares de 1,07 segundos.
Valores Obtenidos:
| Tiempo | X | Y |
| 0 s | 0 mm | 20 mm |
| 1,07 s | 2,3 mm | 15,4 mm |
| 2,14 s | 5,2 mm | 12,9 mm |
| 3,21 s | 6,8 mm | 10,6 mm |
| 4,28 s | 8,5 mm | 8,4 mm |
| 5,35 s | 11 mm | 6,5 mm |
| 6,42 s | 14,5 mm | 4,6 mm |
| 7,49 s | 18,9 mm | 2,8 mm |
| 8,56 s | 24 mm | 1,3 mm |
| 9,63 s | 28,5 mm | 0 mm |
Las mediciones especificadas anteriormente no son las verdaderas, puesto que se encuentran distorsionadas por diferentes causas que no pueden ser evitadas al realizar un estudio, las cuales producen un cierto grado de incertidumbre. Hemos tomado en cuenta aquellas que producen una variación significante en la experiencia, mientras que el resto de ellas no fueron consideradas por entender que son despreciables. Entre esas últimas se encuentran la influencia de las condiciones ambientales al momento de la medición ya sea sobre los instrumentos utilizados, sobre los observadores (nosotros) y sobre el objeto a medir. Las causas de la incertidumbre tenidas en cuenta son las siguientes:
1. Incertidumbre de 3mm sobre los ejes X e Y: determinada como consecuencia de la posible imprecisión de la vista del observador, el diámetro de la mina del lápiz utilizado para marcar las posiciones, el pulso del observador, etc.
2. Incertidumbre de 0,35 segundos en el tiempo: consecuencia del tiempo de reacción del observador al tomar los intervalos con el cronómetro digital.
Después de haber obtenido el gráfico de la trayectoria y haber marcado las respectivas posiciones según los intervalos tomados, graficamos las posiciones en función del tiempo según la dirección horizontal X y la vertical Y. A partir de esos dos gráficos, y utilizando el sistema de cuadrados mínimos, trazamos la tangente en el punto estudiado. Para poder encontrar la velocidad instantánea (Vi) en cada uno de los puntos, debimos dibujar un triángulo rectángulo (en el cual la tangente es la hipotenusa y sus catetos son paralelos al eje del tiempo y al eje de la posición). El tamaño de los lados de los triángulos es relativamente pequeño dado que la velocidad instantánea en un punto es igual al
Eje X
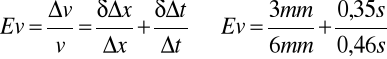
![]()
![]()
| Tiempo | ðx | ðt | v |
| 0 s | (20+3) mm | 0 s | 0 mm/s |
| 1,07 s | (154+3) mm | ( ð 0,35) s | (13,125ð ) mm/s |
| 2,14 s | (129+3) mm | ( ð 0,35) s | (13,3ð ) mm/s |
| 3,21 s | (106+3) mm | ( ð 0,35) s | (12,85ð ) mm/s |
| 4,28 s | (84+3) mm | ( ð 0,35) s | (19,28ð ) mm/s |
| 5,35 s | (65+3) mm | ( ð 0,35) s | (27ð ) mm/s |
| 6,42 s | (46+3) mm | ( ð 0,35) s | (35ð ) mm/s |
| 7,49 s | (28+3) mm | ( ð 0,35) s | (41,25ð ) mm/s |
| 8,56 s | (13+3) mm | ( ð 0,35) s | (42,85ð ) mm/s |
| 9,63 s | (5+3) mm | ( ð 0,35) s | (45ð ) mm/s |
Eje Y
![]()
![]()
![]()
| Tiempo | ðy | ðt | v |
| 0 s | ( +3) mm | 0 s | 0 mm/s |
| 1,07 s | ( +3) mm | ( ð 0,35) s | ( ð ) mm/s |
| 2,14 s | ( +3) mm | ( ð 0,35) s | ( ð ) mm/s |
| 3,21 s | ( +3) mm | ( ð 0,35) s | ( ð ) mm/s |
| 4,28 s | ( +3) mm | ( ð 0,35) s | ( ð ) mm/s |
| 5,35 s | ( +3) mm | ( ð 0,35) s | ( ð ) mm/s |
| 6,42 s | ( +3) mm | ( ð 0,35) s | ( ð ) mm/s |
| 7,49 s | ( +3) mm | ( ð 0,35) s | ( ð ) mm/s |
| 8,56 s | ( +3) mm | ( ð 0,35) s | ( ð ) mm/s |
| 9,63 s | ( +3) mm | ( ð 0,35) s | ( ð ) mm/s |
Teniendo en cuenta los valores de las velocidades instantáneas, calcularemos las aceleraciones instantáneas (a i), utilizando para ello el método anterior. Luego calcularemos la incertidumbre cometida para las aceleraciones.
Eje X
| Tiempo | v | At | a |
| 0 s | 0 mm/s | ||
| 1,07 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 2,14 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 3,21 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 4,28 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 5,35 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 6,42 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 7,49 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 8,56 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 9,63 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
Eje Y
| Tiempo | v | At | a |
| 0 s | 0 mm/s | ||
| 1,07 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 2,14 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 3,21 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 4,28 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 5,35 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 6,42 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 7,49 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 8,56 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
| 9,63 s | ( ð ) mm/s | ( ð 0,35) s | mm/s2 |
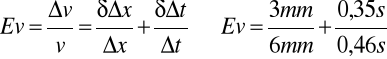
![]()
![]()
![]()
![]()
![]()
Descargar
| Enviado por: | Caro Fernandez |
| Idioma: | castellano |
| País: | Argentina |
