Documentación
Métodos estadísticos
TRABAJO FINAL
METODOS ESTADISTICOS
1º Documentación
Índice:
Identificación de las variables:
justificación de la elección del ------------------------ Pág. 3-4
tipo de variable.
Análisis estadístico de cada ---------------------------- Pág. 5-11
una de las variables:
Análisis conjunto de las ------------------------------- Pág. 12-13
variables:
Conclusiones: ------------------------------------------- Pág. 14
Bibliografía: --------------------------------------------- Pág. 15
Identificación de las variables: justificación de la elección del tipo de variable.
He elegido dos variables para su estudio estadístico, estas son “Nº de Bibliotecas públicas” y “Nº de Habitantes” de las Comunidades Autónomas.
La razón de la elección de estas dos variables, es el interés que tiene su estudio estadístico para los profesionales de la información. Así podremos observar si el número de bibliotecas esta relacionado con el numero de habitantes de las diferentes comunidades autónomas de España, así como, observar diferentes aspectos de las mismas que sin su estudio estadístico no podríamos ver.
Estas dos variables proceden de un muestreo aleatorio, puesto que los individuos de la muestra se eligen al azar, de modo que todos los individuos de la población tienen la misma probabilidad de ser elegidos.
Son variables cualitativas discretas, puesto que sus valores se expresan mediante números y además son variables discretas, porque son valores aislados.
Estas variables han sido extraídas de las bases de datos del Instituto Nacional de Estadística de España y ambas corresponden a datos extraídos de estudios pertenecientes al año 2005.
Las variables son:
| CC. AA. | Nº Habitantes Empadronados | Nº Bibliotecas Públicas |
| Andalucía | 7.849.799 | 645 |
| Aragón | 1.269.027 | 213 |
| Asturias | 1.076.635 | 103 |
| Baleares | 983.131 | 112 |
| Canarias | 1.968.280 | 167 |
| Cantabria | 562.309 | 36 |
| Castilla León | 2.510.849 | 276 |
| C. Mancha | 1.894.667 | 438 |
| Cataluña | 6.995.206 | 412 |
| Valencia | 4.692.449 | 458 |
| Extremadura | 1.083.879 | 394 |
| Galicia | 2.762.198 | 325 |
| Madrid | 5.964.143 | 90 |
| Murcia | 1.335.792 | 43 |
| Navarra | 593.472 | 80 |
| País Vasco | 2.124.846 | 225 |
| Rioja | 301.084 | 23 |
| Ceuta | 75.276 | 2 |
| Melilla | 65.488 | 1 |
Análisis estadístico de cada una de las variables:
-
Tabla de frecuencias:
X = Nº de Bibliotecas Públicas
| Y | ni | Ni | Fi | % |
| 1 | 1 | 1 | 0,05263158 | 5,20% |
| 2 | 1 | 2 | 0,05263158 | 5,20% |
| 23 | 1 | 3 | 0,05263158 | 5,20% |
| 36 | 1 | 4 | 0,05263158 | 5,20% |
| 43 | 1 | 5 | 0,05263158 | 5,20% |
| 80 | 1 | 6 | 0,05263158 | 5,20% |
| 90 | 1 | 7 | 0,05263158 | 5,20% |
| 103 | 1 | 8 | 0,05263158 | 5,20% |
| 112 | 1 | 9 | 0,05263158 | 5,20% |
| 167 | 1 | 10 | 0,05263158 | 5,20% |
| 213 | 1 | 11 | 0,05263158 | 5,20% |
| 225 | 1 | 12 | 0,05263158 | 5,20% |
| 276 | 1 | 13 | 0,05263158 | 5,20% |
| 325 | 1 | 14 | 0,05263158 | 5,20% |
| 394 | 1 | 15 | 0,05263158 | 5,20% |
| 412 | 1 | 16 | 0,05263158 | 5,20% |
| 438 | 1 | 17 | 0,05263158 | 5,20% |
| 458 | 1 | 18 | 0,05263158 | 5,20% |
| 645 | 1 | 19 | 0,05263158 | 5,20% |
| 19 | 1 | 100% |
Y = Nº de Habitantes Empadronados
| Y | ni | Ni | Fi | % |
| 65.488 | 1 | 1 | 0,05263158 | 5,20% |
| 75.276 | 1 | 2 | 0,05263158 | 5,20% |
| 301.084 | 1 | 3 | 0,05263158 | 5,20% |
| 562.309 | 1 | 4 | 0,05263158 | 5,20% |
| 593.472 | 1 | 5 | 0,05263158 | 5,20% |
| 983.131 | 1 | 6 | 0,05263158 | 5,20% |
| 1.076.635 | 1 | 7 | 0,05263158 | 5,20% |
| 1.083.879 | 1 | 8 | 0,05263158 | 5,20% |
| 1.269.027 | 1 | 9 | 0,05263158 | 5,20% |
| 1.335.792 | 1 | 10 | 0,05263158 | 5,20% |
| 1.894.667 | 1 | 11 | 0,05263158 | 5,20% |
| 1.968.280 | 1 | 12 | 0,05263158 | 5,20% |
| 2.124.846 | 1 | 13 | 0,05263158 | 5,20% |
| 2.510.849 | 1 | 14 | 0,05263158 | 5,20% |
| 2.762.198 | 1 | 15 | 0,05263158 | 5,20% |
| 4.692.449 | 1 | 16 | 0,05263158 | 5,20% |
| 5.964.143 | 1 | 17 | 0,05263158 | 5,20% |
| 6.995.206 | 1 | 18 | 0,05263158 | 5,20% |
| 7.849.799 | 1 | 19 | 0,05263158 | 5,20% |
| 19 | 1 | 100% |
-
Gráficos:
Variable X = Nº de Bibliotecas Públicas
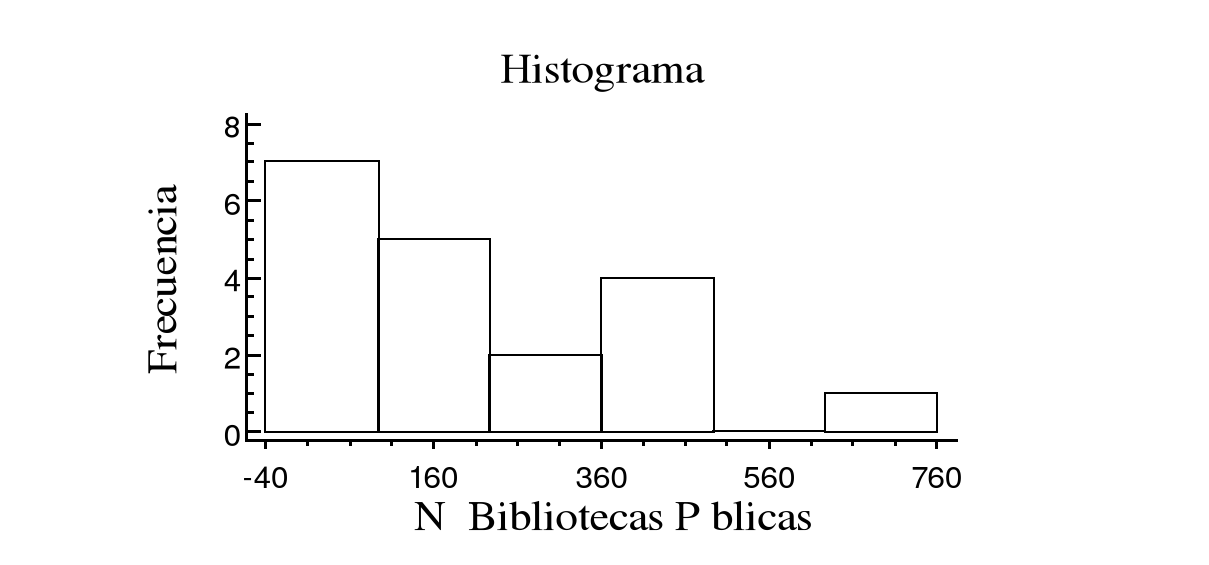
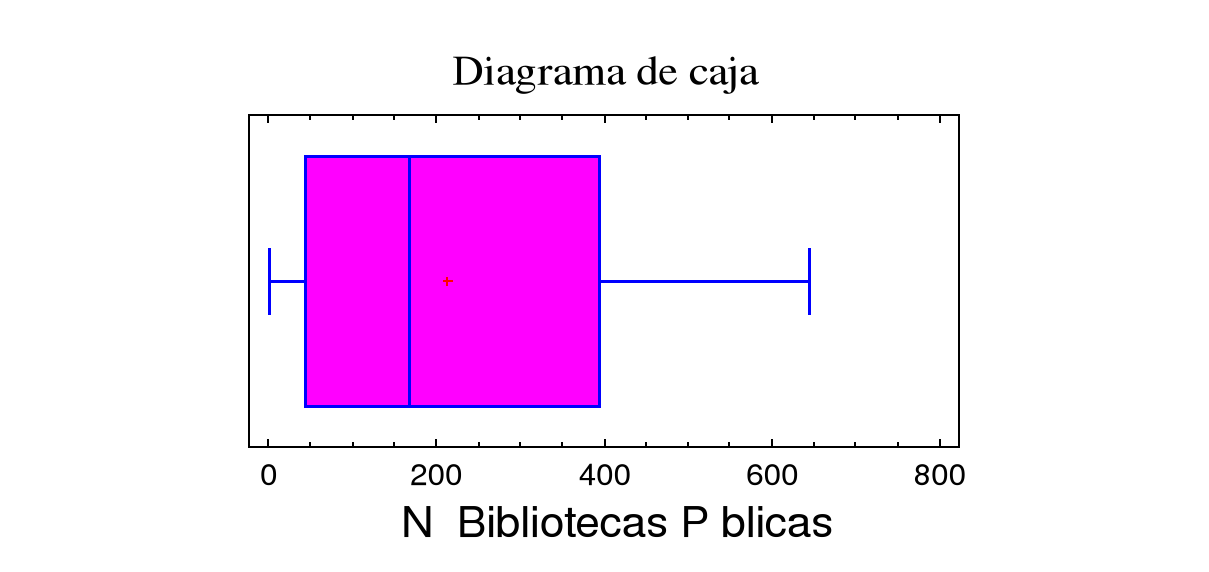
Variable Y = Nº de Habitantes Empadronados
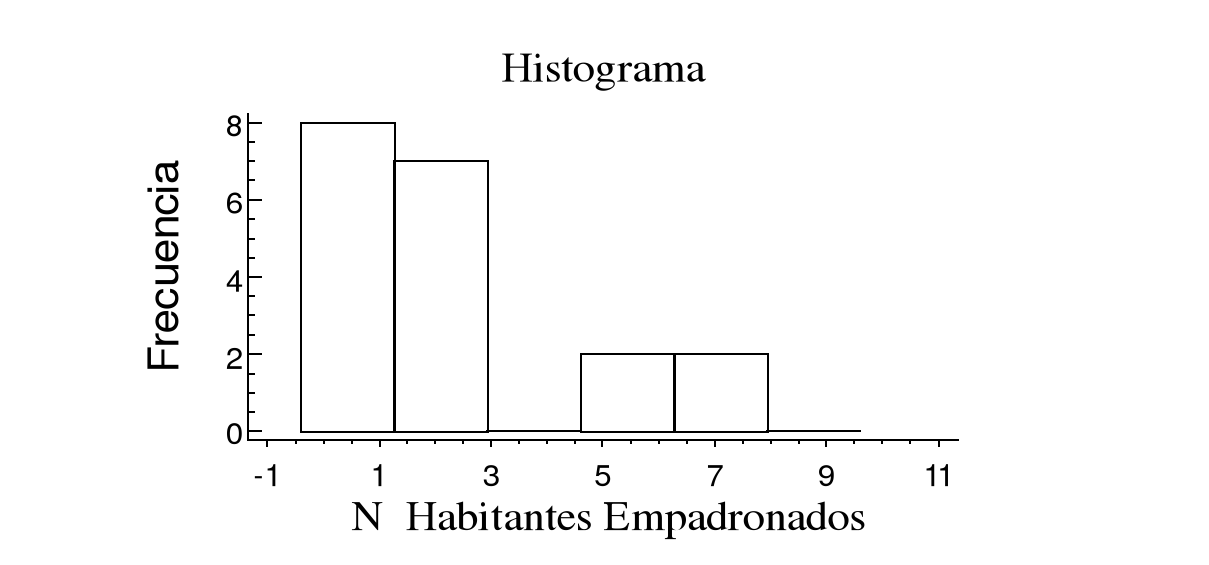
(X 1, E6)
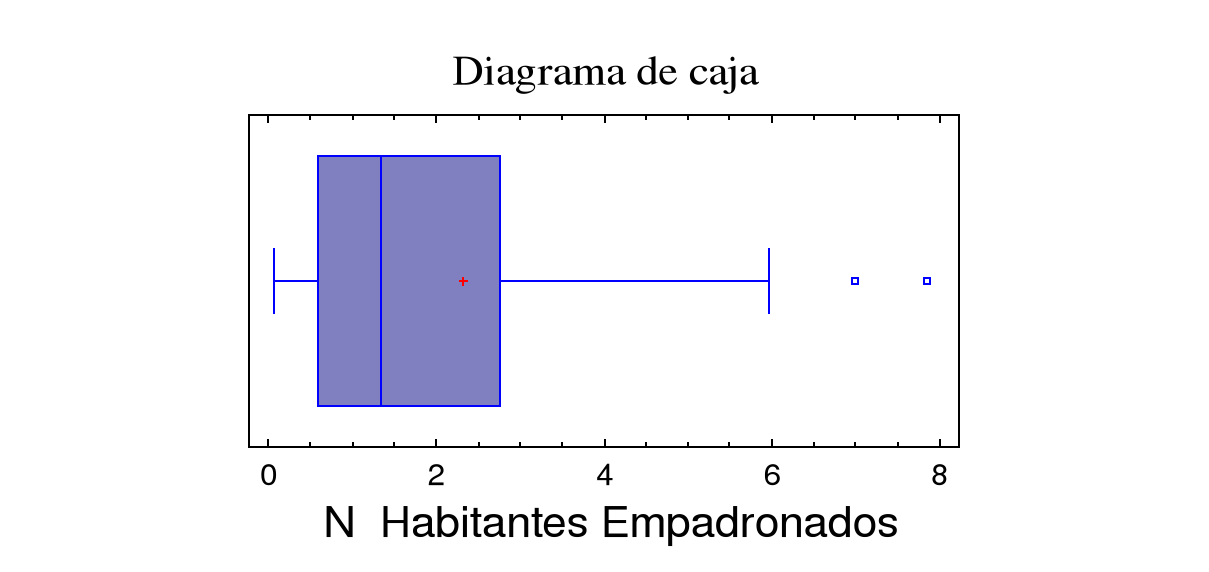
(X 1, E6)
-
Medidas de centralización:
-
Media:
![]()
![]()
; ![]()
![]()
;
![]()
![]()
-
Mediana:
Es el centro físico de los datos, ordenados de mayor a menor, por lo tanto:
Me X = 167
Me Y = 1.335.792
-
Moda:
Es el valor que aparece con una frecuencia mayor, puede haber más de una moda: unimodal, bimodal, trimodal, plurimodal.
En este caso, para ambas variables la moda será plurimodal.
Mo X = todo los valores que aparecen puesto que todos tiene frecuencia 1
Mo Y = todo los valores que aparecen puesto que todos tiene frecuencia 1
-
Cuartiles:

Para X:
![]()
Se coge el valor de la tabla de frecuencias absolutas que sea inmediatamente mayor a 4,75, por lo tanto:
![]()
Y se realiza lo mismo con los demás cuartiles:



Para Y:
![]()
Se coge el valor de la tabla de frecuencias absolutas que sea inmediatamente mayor a 4,75, por lo tanto:
![]()
Y se realiza lo mismo con los demás cuartiles:


-
Medidas de dispersión:
-
Varianza:

Para X:
![]()
Para Y:
![]()
-
Desviación típica:

Para X:
![]()
Para Y:
![]()
-
Coeficiente de Variación:

Para X:
![]()
Para Y:
![]()
Análisis conjunto de las variables:
-
Ajustar un modelo de regresión simple:
Así lo muestra el programa Statgraphics:

-
Escribir la ecuación del modelo resultante. Dibujar el diagrama de dispersión correspondiente y la recta ajustada. Obtener el coeficiente de correlación lineal y el coeficiente de determinación.
La ecuación del modelo resultante es:
Nº Habitantes Empadronados =
453950 + 8776,52*Nº Bibliotecas públicas
-
Diagrama de dispersión:

-
Coeficiente de correlación lineal:
![]()
![]()
-
Coeficiente de determinación:

![]()
Conclusiones:
Respecto al Análisis descriptivo de cada una de las variables, los valores y datos hallados para las dos variables muestran un resumen estadístico de las mismas, de particular interés están los coeficientes de asimetría y curtosis estandarizados que se pueden utilizar para determinar si la muestra procede de una distribución normal. Tanto de una variable como de la otra los valores estadísticos fuera del rango de -2 a +2 indican alejamiento significante de normalidad que tendería a invalidar cualquier test estadístico respecto a la desviación normal. En este caso, el valor del coeficiente de asimetría estandarizado no esta dentro del rango esperado para los datos de una distribución normal. El valor del coeficiente de curtosis estandarizado esta dentro del rango esperado para los datos de una distribución normal.
Respecto al Análisis conjunto de las variables, al comprobar la ecuación del modelo ajustado podemos aclara muchas cosas, existe relación estadísticamente significativa entre Nº de Habitantes Empadronados y Nº de Bibliotecas públicas para un nivel de confianza del 99%.
El estadístico R cuadrado indica que el modelo explica un 48,9% de la variabilidad en Nº de Habitantes Empadronados. El coeficiente de correlación, indica una relación moderadamente fuerte entre las variables. El error estándar de la estimación muestra la desviación típica de los residuos que es 1726000. El error absoluto medio de 1068690 es el valor medio de los residuos. Se examinan los residuos para saber si hay alguna correlación significativa. Dado que el valor es superior a 0,05 no hay indicio de auto correlación serial en los residuos.
Bibliografía:
PEÑA, Daniel. Fundamentos de Estadística. Madrid: Alianza Editorial.
2001. 683 p. ISBN 84-206-8696-4.
Otros: Instituto Nacional de Estadística de España. http://www.ine.es [Consulta 8 de Septiembre de 2006]
Manugistics, Inc. Statgraphics Plus Versión 5. http://www.statgraphics.com [Consulta 8 de Septiembre de 2006]
Apuntes Asignatura Métodos Estadísticos. Curso 2005-2006.
14
Descargar
| Enviado por: | Alex |
| Idioma: | castellano |
| País: | España |
