Estadística
Control estadístico de calidad
Control Estadístico de la Calidad
La evolución del control de calidad
Desde un punto de vista histórico, los cambios principales en el enfoque del trabajo del control de calidad han ocurrido más o menos cada 20 años y se pueden resumir como sigue:
|
| Operador de calidad. En este sistema un trabajador, o por lo menos un número muy reducido de trabajadores , tenían la responsabilidad de la manufactura completa del producto y, por tanto, cada trabajador podía controlar totalmente la calidad de su trabajo. |
|
| Supervisor de control de calidad. En los principios de la década de 1900 surgió el supervisor de control de calidad. Durante este periodo se creo el concepto de la fábrica moderna, en la que muchos hombres agrupados desempeñaban tareas similares en las que pueden se dirigidos por un supervisor, quien asume la responsabilidad de la calidad del trabajo. |
|
| Control de la calidad por inspección. |
|
| Control estadístico de la calidad. Después de al Segunda Guerra Mundial, la enorme producción en masa obligó al surgimiento del control estadístico de la calidad. Esta fase fue una extensión de la inspección , a los inspectores se les proveyó de herramientas estadísticas, tales como muestreo y gráficas de control. La contribución de mayor importancia del control estadístico fue la introducción de la inspección pro muestreo, en lugar de la inspección al 100%. |
La lentitud del crecimiento del control de calidad tuvo poco que ver con problemas del desarrollo de las ideas técnicas y estadísticas. El crecimiento de conceptos como la gráfica de control y los planes fundamentales de muestreo quedó pronto establecido. Los impedimentos fueron la voluntad o la habilidad de las organizaciones para tomar las medidas adecuadas referentes a estos temas.
Gráficas de Control
Es probable que la actividad más reconocida en general del control de calidad sea el control de la materia prima, de los lotes de producción y de las piezas y ensambles durante el proceso de su manufactura. La principal ayuda estadística para estos trabajos, es la gráfica de control y sus modificaciones particulares. Su iniciador fue el Dr, Walter A. Shewhart.
Existen diversas preferencias para el establecimiento de tolerancias del proyecto y límites de especificaciones. En algunas ocasiones, estos límites se determinan cuidadosamente por medio de pruebas; otras veces se han fijado arbitrariamente. La mayoría de la veces, se basan en experiencias anteriores con los materiales y con los procesos de manufactura.
La experiencia de taller tiene mucha importancia cuando se reciban en producción los planos enviados por el ingeniero proyectista. Por ejemplo, el obrero de la máquina producirá un lote de estas piezas, cuya variación en la distancia entre el centroide sea de +- 0.005 in en lugar de +- 0.003 in, que era la indicada. La reacción inmediata del jefe de taller será la de que algo "anormal" esta ocurriendo; puede ser que la broca esté descentrada o que está mal afilada, o bien que la guías de la broca estén desgastadas. Por tanto, se puede pensar la posible acción correctiva, y actuará sobre el taladro.
Existen dos tipos de variables:
1. Variables casuales o accidentales. Que son las que no se pueden controlar ni eliminar, son debidas al proceso mismo.
2. Variables asignables o atribuibles. Que don las que si se pueden controlar y eliminar, se deben al factor humano, a la temperatura, la materia prima, maquinaria, etc.
Definición de las gráficas de control
Se puede definir a la gráfica de control como un método gráfico para evaluar si un proceso está o no en un "estado de control estadístico"
En su forma más usual, la gráfica de control es una comparación gráfica cronológica (hora a hora, día a día) de las características de calidad reales del producto, parte o unidad, con límites que reflejan la capacidad del producirla de acuerdo con la experiencia de las características de calidad de la unidad.
Límites en las gráficas de control por variables
El proceso para el cálculo de los límites de control, en las gráficas por variables, es similar al aplicado para los límites de proceso en las distribuciones de frecuencias, o sea los límites de 3- sigma.
Se han elegido los límites de 3-sigma, porque la experiencia a demostrado es el más útil y económico para la aplicación de los límites de control, puesto que la mayor parte de los valores se encuentran dentro de ese rango (99.73%).
El calculo de las mediciones de tendencia central y dispersión para las diferentes gráficas de control estan auxiliadas por el uso de constantes que se han desarrollado para estos cálculos. Estos factores se encuentran enlistados en unas tablas en las que se dan constantes para calcular los límites de control y estas constantes depende del tamaño de las muestras.
Capacidad del Proceso
La capacidad de un proceso es el rango de variación que, en condiciones normales, un proceso tiene debido a las variables accidentales.
Los pasos para determinar la capacidad de un proceso son:
1. Determinar la característica de calidad.
2. Controlar el proceso. Eliminar todas las variables asignables o atribuibles del proceso.
3. Tomar muestras del proceso. La muestras no deben ser menos de 50 y mínimo con 250 elemento por cada una de ellas.
4. Calcular la media y de la desviación estandar del proceso.
![]()
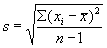
5. Calcular los límites del proceso. Calcular la distribución normal y la capacidad del proceso de acuerdo con las siguientes fórmulas:
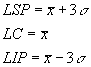
Se comparan los datos obtenidos del proceso con las especificaciones dadas:
|
| Límite Inferior de Especificaciones (LIE) |
|
| Límite Superior de Especificaciones (LSE) |
Si los límites superior e inferior del proceso se encuentran dentro del rango establecido por los límites de las especificaciones, significa que el proceso analizado satisface completamente al cliente.
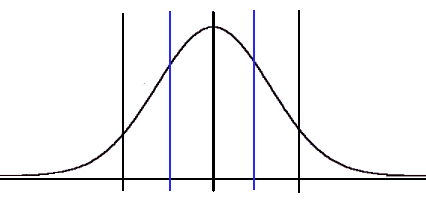
Si uno o ambos límites del proceso se encuentran fuera del rango establecido por las especificaciones, límite superior e inferior, significa que la diferencia entre los limites inferiores y/o superiores (del proceso y las especificaciones) representan los productos defectuosos que se obtienen con nuestro proceso.

Cuando se presenta este caso se pueden tomar diferentes medidas, como pueden ser:
1. Cambiar el proceso por uno que sea capaz de satisfacer completamente las especificaciones.
2. Buscar mercados alternos en los que se puedan vender los productos defectuosos a menor precio.
3. Reprocesar los productos defectuosos.
Con la información obtenida en los pasos anteriores se puede calcular la `Capacidad o Habilidad Potencial del Proceso' (HP) que nos permitirá saber si el proceso que aplicamos es capaz de satisfacer o no las especificaciones.
La forma de calcular la Capacidad Potencial es la siguiente:
![]()
Si la Capacidad Potencial obtenida es mayor a 1, CP>1, significa que nuestro proceso sí es capaz de satisfacer a nuestro cliente. Sin embargo, en la industria se requiere de un margen de error, por lo que se busca que CP > 1.5.
Otra forma de analizar nuestro proceso es comparando la Capacidad del Proceso (CP) con la Capacidad Potencial (HP) de la siguiente manera. Si:
CP > HP El proceso es capaz de satisfacer más y/o mejor al cliente y deben, por lo tanto acoplarse las medias del proceso y de especificaciones para lograrlo.
CP = HP El proceso satisface adecuadamente las especificaciones del cliente.
CP < HP El proceso no es capaz de satisfacer las especificaciones del cliente.
Anomalías en las gráficas de control
Se considera que existen anomalías en las gráficas de control cuando:
1. Existen puntos fuera de los límites de control.
2. Existen 7 puntos consecutivos a un mismo lado de la línea central.
3. Existen 7 puntos consecutivos ascendiendo o descendiendo.
4. Existen 7 puntos consecutivos alternando ascensos y descensos
5. Existen 2 de 3 puntos consecutivos demasiado cerca de uno de los límites de control (inferior o superior)
6. Cuando el 75% de los datos se encuentra alrededor del límite central de control.
7. Cuando uno de los puntos se encuentra extremadamente cerca de los límites de control (casi tocándolo)
GRAFICOS X-R
El gráfico X-R nos ayuda a conocer si nuestro proceso se encuentra dentro de las especificaciones. La medición de las variables y de los rangos de estas nos indican si nuestro proceso es constante o no. Si hay una gran variación en nuestros valores significa que el proceso esta fuera de control o en otras palabras que existen variables asignables o atribuibles que están ocasionando una variación.
Proceso de Implantación del Gráfico X - R
1. Definir característica de calidad (Variable). Selección de la característica que se deba controlar: longitud, área, dureza, etc.
2. Controlar condiciones de proceso. Eliminar todas las variables asignables o atribuibles.
3. Toma de muestras y tamaño de muestra. Tomar K muestras, deben ser más de 25 muestras (K>= 25), el tamaño de muestra es el número de piezas que se van a tomar en cada muestra (n). El tamaño más efectivo que se se ha determinado en diversas aplicaciones industriales ha sido el de 5 unidades; pero puede variar de 2 a 10 unidades. El tamaño de todas las muestras debe ser constante.
Las muestras deben tomarse a intervalos regulares de tiempo, y se van registrando los datos de cada una en el mismo orden en que sean seleccionadas y medidas.
4. Calculó del valor promedio y de la amplitud de la muestra. Cálculo de los promedios X y del rango de las muestras R.
![]()
![]()
5. Calculó de X y R

6. Establecer los límites de control
Límite superior de Control (LSC), Límite Central de Control (LCC) y límite Inferior de Control (LIC)
Límites para la gráfica X

Límites para la gráfica R

7. Graficar
8. Analizar los datos y modificar los límites en caso de que haya puntos fuera de los límites. Analizar los promedios y las amplitudes de cada muestra con relación a los límites de control. Ajustar los límites eliminando los puntos que se encuentran fuera de los límites y volviendo a calcular estos últimos.
9. Calcular la capacidad del proceso
10. Comparar el proceso con los límites de especificaciones. Analizar los datos para ver si no existe un punto fuera de los límites de control y revisar si existen variables asignables o atribuibles en el proceso.
GRAFICOS P
El gráfico P sirve para detectar artículos defectuosos cuando se están analizando variables por atributos, nos proporcionará la fracción o porcentaje de artículos defectuosos en la población que se encuentra bajo estudio.
Los pasos para obtener el gráfico P
1. Definir la característica de calidad (atributo) que se desea analizar. Olor, sabor, medida específica, etc. Lo tiene o no lo tiene.
2. Controlar las condiciones del proceso. Eliminar las variables asignables o atribuibles del proceso.
3. Tomar un número K de muestras. El tamaño de la muestra debe de ser variable, es decir las muestras no son del mismo tamaño. El número de muestras no debe ser menor a 20, y cada muestra debe tener por lo menos 50 elementos.
4. Tabular resultados de acuerdo a la siguiente tabla:
| Número de muestra | Tamaño de muestra (n) | Número de productos defectuosos (np) | Fracción de defectuosos ( p ) p= np/p |
| 1 | n1 | Np1 | p1 |
| 2 | n2 | Np2 | p2 |
| .... | .... | .... | .... |
| k | nk | npk | pk |
5. Cálculo de ![]()
.A continuación se calcula la media (promedio) del tamaño de las k muestras.
![]()
6. Se genera un rango alrededor de la media de +20%.
a) Si todas las muestras se encuentran dentro de este rango, continuamos con el paso 7
b) Si solamente una de las muestras no se encuentra dentro de este rango, dicha muestra se elimina y se vuelve al paso número 5
c) Si más de una muestra se encuentra fuera del rango establecido, entonces a partir del paso. 7 todo se hará de manera independiente para cada muestra.
7. Cálculo de los valores promedio. Posteriormente se calcula la media (promedio) de la fracción de defectuosos (p).
![]()
8. Cálculo del los límites de control del proceso. El siguiente paso es el cálculo de los límites de control de nuestro proceso.
Dado que se está realizando el análisis de los atributos ( se tiene o no se tiene) se utiliza una distribución binomial para calcular los límites de control. Los cuales están dados por:
Límite superior de Control (LSC), Límite Central de Control (LCC) y límite Inferior de Control (LIC)

9. Graficar. A continuación se realiza la gráfica, en la cual se marcan los límites de control y en relación a ellos se grafica el número de defectuosos de cada una de las muestras.
10. Comparar el proceso con los límites de especificaciones. Observar el comportamiento del proceso de acuerdo con la gráfica y sacar conclusiones.
GRAFICO np
El gráfico np sirve para detectar la fracción de artículos defectuosos cuando se están analizando variables por atributos, nos proporcionará la fracción o porcentaje de artículos defectuosos en la población que se encuentra bajo estudio.
Los pasos para obtener el gráfico np
1. Definir la característica de calidad (atributo) que se desea analizar.
2. Controlar las condiciones del proceso. Eliminar todas las variables asignables o atribuibles del proceso.
3. Tomar un número K de muestras. Las muestras deben de ser de tamaño constante, es decir todas las muestras son del mismo tamaño. El número de muestras no debe ser menor a 20, y cada muestra debe tener por lo menos 50 elementos.
4. Tabular resultados de acuerdo a la siguiente tabla
| Número de muestra | Tamaño de muestra (n) | Número de productos defectuosos (np) | Fracción de defectuosos ( p ) p= np/p |
| 1 | n | np1 | p1 |
| 2 | n | np2 | p2 |
| .... | .... | .... | .... |
| k | n | npk | pk |
5. Cálculo de ![]()
Posteriormente se calcula la media (promedio) del número de artículos defectuosos de todas las muestras.
![]()
6. Cálculo de los Límites de Control del Proceso.
Dado que se está realizando el análisis de los atributos ( se tiene o no se tiene) se utiliza una distribución binomial para calcular los límites de control. Los cuales están dados por:
Límite superior de Control (LSC), Límite Central de Control (LCC) y límite Inferior de Control (LIC)

9. Graficar. A continuación se realiza la gráfica, en la cual se marcan los límites de control y en relación a ellos se grafica el número de defectuosos de cada una de las muestras.
10. Comparar el proceso con los límites de especificaciones. Observar el comportamiento del proceso de acuerdo con la gráfica y sacar conclusiones.
Descargar
| Enviado por: | Armando Suarez Rodriguez |
| Idioma: | castellano |
| País: | Perú |
