Matemáticas
Análisis y Cálculo
1. TEORÍA DE CONJUNTOS
CONCEPTO DE PERTENENCIA: "ð"
Sea el conjunto A = ða, bð
ð a ð A
ð b ð A ð c ð A
CONCEPTO DE SUBCONJUNTO: "ð"
A ð B ð ð x ð A ð x ð B, ð x ð
ð ð A, ð A
A ð A, ð A
CONJUNTOS ESPECIALES
Conjunto Vacío: ð = ð ð
ððð ð ð ð ð0ð
Conjunto Universo: "U"
Es aquel formado por todos los elementos involucrados en el problema.
Conjunto Potencia: "P(A)"
Es el formado por todos los subconjuntos del conjunto A.
ð P(A) = 2n ; n : nº de elmentos de A.
OPERACIONES
UNIÓN: A ð B = ðx / x ð A ð x ð Bð
INTERSECCIÓN: A ð B = ðx / x ð A ð x ð Bð
A ð B ð A ð B = A
A ð B = ð ð A y B son disjuntos.
DIFERENCIA: A - B = ðx / x ð A ð x ð Bð
COMPLEMENTO: Ac = ðx / x ð A ð x ð Uð
(A ð Ac) = U
(A ð Ac) = ð
ð c = U ; Uc = ð ; Ac = U - A
2. CONJUNTOS NUMÉRICOS
DIAGRAMA DE CONJUNTOS
IN: Naturales Q*: Irracionales
INo: Cardinales IR: Reales
Z: Enteros I: Imaginarios
Q: Racionales C: Complejos
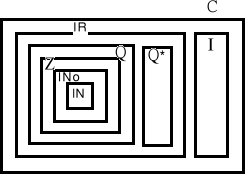
IN ð INo ð Z ð Q ð IR ð C
Q ð Q* = ð ; Q ð Q* = IR
IR ð I = ð ; IR ð I = C
Dado un conjunto A, se define Ac como complemento de A al conjunto de elmentos del universo que no pertenece a A.
NÚMEROS ENTEROS
CONJUNTO Z
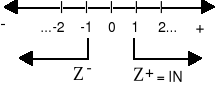
Z = Zð ð ð0ð ð Z+
CONSECUTIVIDAD NUMÉRICA
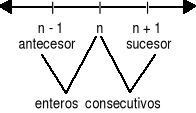
PARIDAD E IMPARIDAD
Números Pares:
Son de la forma: 2n; n ð Z
![]()
Números Impares:
Son de la forma: 2n - 1; n ð Z
![]()
Números Primos:
Un número p > 1 se llama primo si es divisible sólo por 1 y por p. Algunos primos conocidos:
2 - 3 - 5 - 7 - 11 - 13 - 17 -...- 1234567891-
NOTA: El cero no se define como par ni como impar. El 1 no es primo.
PRIORIDAD DE OPERACIONES
1º Potencias
2º Multiplicación y/o división
3º Suma y/o resta
Calcular el M.C.M. entre 6, 9 y 12.
Se realizan divisiones sucesivas por los factores primos hasta lograr un 1 en cada columna.
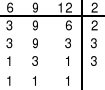
ð M.C.M. = 2 ð 2 ð 3 ð 3 = 36
Se realizan divisiones sucesivas por sólo los factores primos que dividan a todos los números. Esto se realiza sucesivamente hasta lograr en las columnas números primos entre sí.

Primos entre sí.
ð M.C.D. = 2 ð 3 = 6
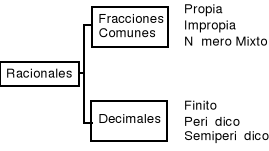
NÚMEROS RACIONALES
DEFINICIÓN
Q = ðx = ![]()
/ a ð b ð Z, b ð 0ð
a : numerador
b : denominador
x : cuociente
AMPLIFICACIÓN Y SIMPLIFICACIÓN
Amplificación:
![]()
Simplificación:

- Comparación de 2 fracciones

- Igualación de denominadores (2 o más fracciones)
Sean las siguientes fracciones:
![]()
M.C.M. entre 7, 14 y 56 es 56; luego, amplificando tenemos:

OPERATORIA CON FRACCIONES
Suma y Resta:
![]()
Multiplicación:
![]()
División:
![]()
Decimal Finito:
![]()
Decimal Periódico:

Decimal Semiperiódico:

POTENCIAS
DEFINICIÓN
![]()
PROPIEDADES Y EJEMPLOS

POTENCIAS DE 10

APLICACIÓN DE LAS POTENCIAS DE 10
![]()
![]()
SIGNO DE UNA POTENCIA
n ![]()
PAR POSITIVO
IMPAR SIGNO DE a
Ejemplo : -22 = -2 ð 2 = -4 ; (-2)2 = (-2) ð (-2) = 4
RAÍCES
DEFINICIÓN ![]()
PROPIEDADES
![]()
![]()
![]()
![]()
ÁLGEBRA
TÉRMINO ALGEBRAICO
![]()
EXPRESIÓN ALGEBRAICA
![]()
Clasificación:
i. Monomio: 3x2 b
ii. Polinomio:
-
Binomio : 3x2 b + 2a
-
Trinomio: 3x2 b + 2a - 2xb
Suma y Resta:
3x + (8x - 5xy) = 3x + 8x - 5xy = 11x - 5xy
Multiplicación:

Productos Notables:
i. Cuadrado de binomio:
![]()
ii. Suma por diferencia:
![]()
iii. Binomio por binomio:
![]()
iv. Cubo de binomio:
![]()
v. Cuadrado de trinomio:
(x+y+z)2 =x2 + y2 +z2 +2xy+2xz+2yz
Factorización:
i. Sacar factor común:
![]()
ii. Por agrupación:

iii. Binomio por binomio:
![]()
iv. Suma y diferencia de cubos:
![]()
División:
![]()
Determinación del M.C.D. y M.C.M.
Entre términos algebraicos.
i. M.C.D.: Equivale el factor común con su menor exponente.
![]()
i. M.C.M.: Menor término que los contiene a todos. Todos los factores con su mayor exponente.
![]()
Entre expresiones algebraicas.
Aquí es recomendable factorizar previamente las expresiones.
I. M.C.D.:

ii. M.C.M.:

ECUACIONES Y SISTEMAS DE ECUACIONES
ECUACIONES
Como ejemplo, se resolverá
![]()

SISTEMAS DE ECUACIONES
Métodos de resolución:
-
Eliminación por Reducción
-
Eliminación por Sustitución
Método de eliminación por reducción Ejemplo

OBSERVACIÓN
Dado el sistema :
![]()
Si a ð e - b ð d ð 0, entonces tiene una solución.
Si a ð e - b ð d = 0, entonces NO tiene solución o tiene infinita soluciones.
Método de eliminación Ejemplo
por sustitución:

RAZONES Y PROPORCIONES
Razón : Relación (división entre dos cantidades homogéneas.
Proporción : Igualdad de dos razones.

SERIE DE RAZONES
![]()
![]()
PROPORCIÓN DIRECTA
X es directamente proporcional a Y si:
![]()
PROPORCIÓN INVERSA
X es inversamente proporcional a Y si:
![]()
PORCENTAJES
El porcentaje es siempre una proporción directa, ![]()
TANTO POR CIENTO DE UN NÚMERO
El a % de T es:
![]()
RELACIÓN PORCENTUAL DE DOS NÚMEROS
¿Qué % es a de T?
![]()
CÁLCULO DEL TOTAL, CONOCIDO EL PORCENTAJE
¿De qué número, a es el b%?
![]()
PORCENTAJES SUCESIVOS
El p% del q% de A es x
![]()
PORCENTAJES ESPECIALES

PROBLEMAS DE PLANTEO
CONDUCTAS
-
Comprensión del problema.
-
Preparación de un plan: organizarlos datos, diagramas, buscar un patrón, plantear una ecuación.
-
Resolución del plan.
-
Verificación de la respuesta.
-
Un método alternativo (trabajar hacia atrás).
CONTENIDOS
-
Traducción del lenguaje cotidiano al lenguaje matemático.
-
Plantear una ecuación.
ENUNCIADOS MÁS FRECUENTES
El duplo (doble) : 2x
El triple : 3x
El cuádruplo : 4x
El cuadrado : x2
El consecutivo : x + 1 (x ð Z)
El anterior : x - 1 (x ð Z)
Tres números consecutivos:
(n - 1) ; n; (n + 1)
Tres pares consecutivos:
(2n - 2) ; 2n; (2n + 2)
Tres impares consecutivos:
(2n - 1) ; (2n + 1) ; (2n + 3)
Descargar
| Enviado por: | Patita De Pollo |
| Idioma: | castellano |
| País: | Chile |
