Física
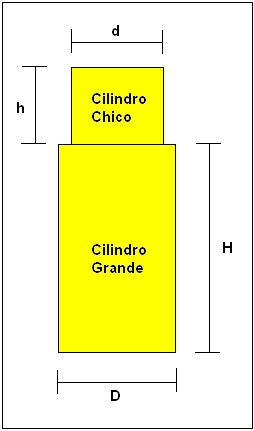
Volumen del cilindro
Datos y Resultados
Gravedad ![]()
Masa ![]()
Diámetro Grande (D) ![]()
Diámetro Chico (d) ![]()
Altura Grande (H) ![]()
El volumen del cilindro grande es constante y se obtiene de la siguiente manera, ![]()
donde h es la altura que se desplaza el otro cilindro, como en este caso queremos sacar el puro volumen del cilindro grande ![]()
y obtenemos la siguiente formula: ![]()
.
El peso del pistón completo se
obtiene a partir de la formula:
![]()
Las siguientes mediciones fueron variables, estas son:
-
La altura del cilindro chico, que a su vez define el volumen del cilindro chico.
-
La tensión marcada por el sensor de fuerza.
El volumen del cilindro chico se obtiene de la siguiente manera:
![]()
Donde d es el diámetro medido y será utilizado como constante, por lo que la única variable es h que es la altura que este cilindro tendrá en cada muestra.
| Medición | Vol. Chico (m3) +/- .000006 m | Altura h (m) +/- .00025 m | Tensión (N) | Desviación Tensión (N) | Fr. Flotación (N) +/- .4 N |
| 1 | 0 | 0 | 1.492 | 0.02 | 0.2573 |
| 2 | 2.49005E-06 | 0.0127 | 1.464 | 0.019 | 0.2853 |
| 3 | 3.03904E-06 | 0.0155 | 1.458 | 0.02 | 0.2913 |
| 4 | 3.72527E-06 | 0.019 | 1.449 | 0.019 | 0.3003 |
| 5 | 5.882E-06 | 0.03 | 1.425 | 0.018 | 0.3243 |
| 6 | 6.60745E-06 | 0.0337 | 1.418 | 0.02 | 0.3313 |
La grafica en la que se relaciona a la fuerza resultante con el volumen desplazado queda de la siguiente manera:
La ecuación de esta grafica es ![]()
El valor obtenido de ![]()
.
La incertidumbre de m y b se pueden calcular con las siguientes ecuaciones:


Donde Sy se obtiene con 
donde d se obtiene con ![]()

Por lo que tenemos que ![]()
es:

También tenemos que b es:

Análisis de Resultados
Primero tenemos que hacer nuestro diagrame de cuerpo libre para poder entender lo que esta sucediendo. De este diagrama tenemos la siguiente ecuación:
![]()
Por lo que tenemos la siguiente comparación ![]()
![]()
y la ecuación nos queda ![]()
donde si despejamos y nos queda ![]()
. De allí viene la relación lineal que este fenómeno tiene, la ecuación final con todo y unidades quedaría así:
![]()
En la ecuación de la grafica tenemos que la pendiente es -11289, este número es la multiplicación de la densidad de la glicerina con el valor de la gravedad ![]()
, por lo que si lo dividimos obtenemos el valor de la densidad de la glicerina:
![]()
Si el valor teórico de la densidad es de ![]()
y el que obtuvimos es ![]()
tenemos entonces que el porcentaje de error es de:

También tenemos que el valor teórico de b=1.7493, el valor que obtuvimos en la grafica fue b=1.7344 entonces tenemos que nuestro porcentaje de error fue:

La pendiente de la grafica fue negativa, esto es totalmente lógico ya que si tenemos que el volumen desplazado es 0m3 tenemos que la tensión es igual al peso y si el volumen empieza a aumentar, la tensión del sensor comienza a disminuir, esto causado por la fuerza de flotación. Si la pendiente no fuese negativa, al aumentar el volumen teóricamente aumentaría la tensión lo cual no es lógico ya que la fuerza de flotación tiene una relación directa con la densidad del líquido y con el volumen que el objeto desplaza.
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | México |
