Matemáticas
Teorema de Pitágoras
Teorema De Pitágoras
2.002
NOMENCLATURA
Introducción ( Temática)
Objetivo General
Objetivos Específicos
Contenido
Historia, Antecedentes y Referencias Biográficas
Ejemplos Textuales y Bibliográficos
Problemas
Actividad
Bibliografía
6. Conclusiones
INTRODUCCIÓN
Temática:
Si un triángulo tiene lados de longitud (a, b, c), con los lados (a, b) formando un ángulo de 90 grados ("ángulo recto"), tenemos que
a2 + b2 = c2
Un ángulo recto se puede definir como el ángulo formado cuando dos líneas rectas se cruzan de tal forma que los cuatro ángulos que forman son iguales. El teorema también se puede definir de otra forma: si las longitudes de los tres lados (a, b, c) de un triángulo satisfacen la relación anterior, el ángulo entre los lados a y b debe ser de 90 grados.
1. Objetivo General:
* El objetivo general de este trabajo y de el Teorema de Pitágoras es que en un triángulo rectángulo, el cuadrado del lado más largo es igual a la suma de los otros dos lados. Es decir:
2. Objetivos Específicos:
-
Reconocer que el Teorema de Pitágoras surge entre las matemáticas del mundo moderno y no podríamos vivir sin el.
-
Pitágoras y su grupo de alumnos llamados, los Pitagóricos, fueron los que pensaron el hecho de que 1+2+3+4 daba 10 y que estos números se podían ordenar en un triángulo al que llamaban tetraktys.
3. Contenido:
3.1 Historia, Antecedentes y Referencias Biográficas...
Pitágoras nació en la isla de Samos en el mar Egeo. ( De allí, Pitágoras De Samos) Aproximadamente en 530 AC.
Pitágoras es más conocido por el teorema que lleva su nombre, pero fue sólo una de tantas relaciones que su grupo encontró en los números. Los pitagóricos se fascinaban con el hecho de que 1+2+3+4 daba 10 y que estos números se pudieran ordenar en un triángulo que ellos llamaban tetraktys. Su postura de que todo el universo se basaba en un orden místico o kosmos, se vio bastante fortalecida cuando descubrieron que existía una conexión entre el tetraktys y la música
3.2 Ejemplos Textuales y Ejemplos Bibliográficos
A.
Por ejemplo, un triángulo con los lados a = 3, b = 4, c = 5 (pulgadas, pies, metros,... lo que sea) es rectángulo porque
a2 + b2 = 32 + 42
= 9 + 16 = 25 = c2
B.
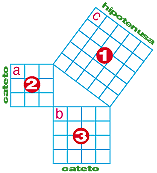
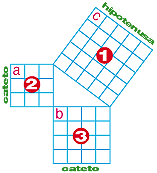
Hemos construido un cuadrado sobre cada lado del triángulo rectángulo.
Pitágoras dice que el cuadrado 1 tiene su área igual a la suma de los cuadrados 2 y 3.
De acuerdo al cuadriculado, el cuadrado 1 tiene un área de 25 cuadros. Al sumar los 9 cuadros del cuadrado 2 y los 16 cuadros del 3 obtenemos 25. Entonces, se cumple:
C2= A2 + B2
C.
-
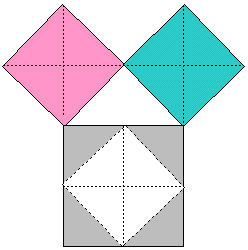
Dibujamos un triángulo rectángulo y sobre cada uno de sus lados, construimos un cuadrado. Dibujamos en cartoncillo o en madera la plantilla completa. Se recortan, en cartulina y por las líneas punteadas, los cuadros rosado y celeste.
Se pide al estudiante que coloque las piezas recortadas sobre el cuadro gris, de tal forma que agote toda el área.
3.3 Problemas
1
El cuadrado de un cateto de un triángulo rectángulo es 16, y el otro cateto mide 3, ¿ Cuánto mide la hipotenusa? Operación:
1 H2 = C12 + C12 C12 = 16
C12 = 3 = 32 = 9
2 H2 = 16 + 9 = 25
3 H2 = 25 H = 5
Rta: La hipotenusa mide 5
2
La hipotenusa de un triángulo rectángulo es 5, y uno de sus catetos es 3, ¿ Cuánto mide el cateto restante? Operación:
1 (5)2 = (3)2 + C22 4 C22 = 16
2 25 = 9 + C22 5 C22 = 16
3 25 - 9 = C22 6 C2 = 4
Rta: El cateto restante mide 4
3
Si la hipotenusa de un triángulo rectángulo mide 7,071, y los catetos tienen potencias exactas, ¿ Cuanto miden los catetos? Operación.
1 7,0712 = 50.000
2 C12 = 5 3 52 = 5x5 = 25 4 25+25=50
C22 = 5 52 = 5x5 = 25
Rta: Los catetos miden 5
4. Actividad
Materiales:
1 Octavo de Cartulina, 1 Lápiz y Tijeras
Pasos:
-
Dibuja un triángulo rectángulo, y sobre cada uno de sus lados traza un cuadrado.
-
Recorta el cuadrado más pequeño.
-
Sobre el cuadrado mediano traza dos rectas que pasando por su centro sean paralelas a los lados del cuadrado grande.
-
Ahora recorta el cuadrado mediano en cuatro trozos siguiendo las rectas anteriores.
¿ Eres capaz de acoplar todos los trozos recortados de forma que llenen el cuadrado grande?
Has demostrado un teorema. ¿Cuál?
Bibliografía
CONTENIDO:
Historia, Antecedentes y Referencias Biográficas:
-
El Tiempo. (2002).Libro GENIAL. Bogotá. Editorial El Tiempo. Págs.: 37-39
Ejemplos Textuales y Bibliográficos:
Problemas:
Actividad:
6. Conclusiones:
Sirve o no sirve?:
Es muy útil en cuanto a geometría ya que representa varios números en una sola figura geométrica, utilizando una operación sencilla y fácil de entender.
Qué aprendí?:
Además de aprender que en un triángulo rectángulo, el cuadrado del lado más largo es igual a la suma de los otros dos lados, aprendí como desarrollar ejercicios de geometría, y como despejar una fórmula; lo cuál me sirve mucho para los siguientes años en el área de matemáticas...
Descargar
| Enviado por: | Padme123 |
| Idioma: | castellano |
| País: | Colombia |
