Matemáticas
Razón áurea
NUMERO AUREO
Hagamos un experimento: con un papel y un lápiz, dibuja una recta de la dimensión que quieras. Fíjate bien en ella, y después , divídela en dos partes desiguales mediante un pequeño trazo, de tal manera que los dos segmentos sean equilibrados y proporcionalmente agradables. Mídelas. Podrás comprobar que la menor es aproximadamente un 62% de la mayor y que ésta es un 62% de la recta completa. Fray Paciolo di Borgo, monje italiano, enuncia en el 1509 una fórmula matemática cuya aplicación da una constante a la que denominó Número de Oro o Divina Proporción.Ya utilizada de forma empírica en la antiguedad, ésta Divina Relación se encuentra cuando, realizando el ejercicio anterior, el segmento menor está en la misma proporción con respecto al mayor que éste con respecto a la suma de ambos, es decir, con respecto al total. Este número equivale al 62% y es exactamente 0.618.
RECTÁNGULO ÁUREO
|
Un rectángulo especial es el llamado rectángulo áureo. Se trata de un rectángulo armonioso en sus dimensiones. | ||
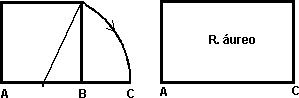
| Dibujamos un cuadrado y marcamos el punto medio de uno de sus lados. Lo unimos con uno de los vértices del lado opuesto y llevamos esa distancia sobre el lado inicial, de esta manera obtenemos el lado mayor del rectángulo. |
| |
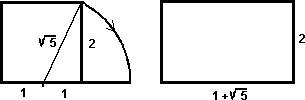
| Si el lado del cuadrado vale 2 unidades, es claro que el lado mayor del rectángulo vale 1+ 5 por lo que la proporción entre los dos lados es: (1+ 5 ) /2 |
| |
A este número se le llama número de oro, se representa por el símbolo Ø y su valor es 1,61803..., lo obtuvieron los griegos al hallar la relación entre la diagonal de un pentágono y el lado. El nombre de "número de oro" se debe a Leonardo da Vinci.
|
| En "el hombre ideal" de Leonardo, el cociente entre el lado del cuadrado y el radio de la circunferencia que tiene por centro el ombligo, es el número de oro. |
|
| Otra propiedad de este rectángulo es que si se colocan dos iguales como en la figura de la derecha, se forma otro rectángulo áureo más grande. |
|
.
Los egipcios ya conocían esta proporción y la usaron en la arquitectura de la pirámide de Keops (2600 años a.C.).
| Aparece en pinturas de Dalí, en la Venus de Boticelli. Esta razón también la usaron en sus producciones artistas del Renacimiento. En España, en la Alhambra, en edificios renacentistas como El Escorial ... y en la propia Naturaleza en las espirales de las conchas de ciertos moluscos. |
|
|
| Los griegos también la usaron en sus construcciones, especialmente El Partenón, cuyas proporciones están relacionadas entre sí por medio de la razón áurea. |
El símbolo Ø para la relación áurea fue elegido por el matemático americano Mark Barr. La letra fue elegida porque era la primera del nombre de Phidias que solía usar la relación áurea en sus esculturas.
También se ha usado en el diseño del DNI, en la construcción de muebles, marcos para ventanas, camas, etc.
|
|
LA SUCESIÓN DE FIBONACCI
Consideremos la siguiente sucesión de números:
1, 1, 2, 3, 5, 8, 13, 21, 34...
Cada número a partir del tercero, se obtiene sumando los dos que le preceden. Por ejemplo, 21 = 13 + 8; el siguiente a 34 será 34 + 21 = 55.
Esta sucesión es la llamada "sucesión de Fibonacci" (Leonardo de Pisa 1170-1240).
Los cocientes (razones) entre dos números de la sucesión, se aproximan más y más al número áureo (1'61803...).
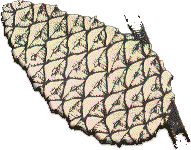
| Esta sucesión de números aparece en la Naturaleza en formas curiosas. Las escamas de una piña aparecen en espiral alrededor del vértice. Si contamos el número de espirales de una piña, encontraremos que siempre es igual a uno de los números de la sucesión de Fibonacci. |
|
|
| Esta sucesión también aparece en el estudio de las leyes mendelianas de la herencia, en la divergencia foliar, en la formación de la concha de algunos moluscos... |
|
| Una manera práctica de dibujar una espiral es mediante la construcción rectangular en las espirales de cuadrados; se trata de dibujar el cuadrante de un círculo en cada nuevo cuadrado que se añada. |
En la construcción anterior, se empieza con un cuadrado de 1 unidad de lado (el nº 1), se añade uno igual para formar un rectángulo de 2 x 1, a continuación añadimos un cuadrado de 2 x 2 (el nº 3) para formar un rectángulo de 3 x 2; después un cuadrado de 3 x 3 (el nº 4), de manera que el siguiente rectángulo es 5 x 3, el siguiente cuadrado es 5 x 5 (el nº 5), y así sucesivamente.
SUCESIÓN DE FIBONACCI Y LA RAZÓN ÁUREA
Consideremos la siguiente sucesión de números: 1, 1, 2, 3, 5, 8, 13, 21...
| Las razones entre ellos son: |
|
Si cogemos dos números cualesquiera como números de partida y formamos una sucesión de Fibonacci sumando siempre los dos últimos números, las razones serian:
Empezamos por 3 y 7; la sucesión sería: 3, 7, 10, 17, 27, 44, 71, 115...
| Las razones son: |
|
Independientemente de los números que encabecen la sucesión, las razones se aproximan más y más al número 1'61803...
Este número fue estudiado por los griegos. Estamos ante el numero aúreo, su valor
| exacto es: |
| y se representa con el símbolo Ø. |
| Los griegos obtuvieron este número al hallar la relación entre la diagonal del pentágono regular y su lado. Esto hace posible construir un pentágono regular usando regla y compás.
|
|
|
| Al trazar las diagonales de un pentágono resulta la estrella pentagonal o estrella de Italia, era el símbolo de la escuela pitagórica y servía a los pitagóricos para reconocerse entre sí. |
Podemos investigar otras reglas similares a la de Fibonacci y generar otras sucesiones interesantes, por ejemplo, comenzar con dos números, siendo el siguiente el que resulta de sumar el último con dos veces el anterior: 3, 3, 9, 15, 33, 63, 129, 255...
Con esta sucesión la razón se aproxima cada vez más a 2.
Descargar
| Enviado por: | Musclepanx |
| Idioma: | castellano |
| País: | España |