Economía y Empresa
Planeación estratégica de la producción
I N T R O D U C C I O N
El problema de la planeación de la producción juega un papel preponderante en las operaciones de manufactura. El problema consiste en decidir qué tipo y cuánto se debe fabricar de un producto en los periodos de tiempo futuros. Este tipo de decisiones se basan en una gran cantidad de factores, incluyendo las horas-máquina y las horas-hombre disponibles por periodo, los márgenes de ganancias deseados, los costos de almacenaje, etc. La estimación de la demanda de productos manufacturados para los periodos planeados es de particular importancia en este tipo de problemas. En este proyecto se está interesado en el problema de la planeación de la producción incluyendo en los modelos, la aleatoriedad que existe en la estimación de las futuras demandas. Este problema se abordará utilizando dos variantes de la técnica Monte Carlo basados en técnicas de optimización estocástica, las cuales reciben en la literatura normal, el nombre de métodos de “optimización por simulación”'. En la primera variante, se supone que se conoce la función de densidad de la demanda actual (la cual se supone una función continua) y a partir de ésta, se aproximará una solución mediante el promedio de los valores de la muestra al valor esperado de la función correspondiente. El segundo enfoque se utiliza cuando existe una información incompleta acerca de la densidad asociada a la demanda.
La planificación de la capacidad es fundamental para el éxito a largo plazo de una organización. La capacidad excesiva puede ser tan fatal como la capacidad insuficiente, lo cual se demuestra en la práctica administrativa. Al escoger una estrategia de capacidad los directivos deben analizar preguntas como: ¿Cuánto “colchón” se necesita para manejar la demanda incierta y variable? ¿Debemos expandir la capacidad antes de que la demanda se manifieste claramente o es mejor esperar hasta que la ultima se perfile con mayor certeza?. Se requiere un método sistemático para contestar estas y otras preguntas similares y para desarrollar una estrategia de capacidad que sea apropiada para cada situación.
En general este tipo de problemas ha sido muy poco explorado a pesar de constituir en la actualidad uno de los casos más comúnmente encontrados dentro de la práctica de la ingeniería industrial. Como estrategia de cálculo para abordar este problema, se probarán una gran variedad de casos de subproblemas de planeación del tipo recursos para un sólo producto y recursos para productos múltiples para demostrar la efectividad de la técnica desarrollada bajo condiciones variantes. Como hipótesis de trabajo de esta propuesta se plantea el hecho de que es factible encontrar una solución y ahora a través de la modelación matemática estocástica de sistemas como el aquí planteado.
El modelo matemático asociado a la descripción del sistema es no diferenciable en la función objetivo, y convexo con respecto a la variable de decisión. La perturbación del modelo se obtiene a partir de una variable aleatoria con densidad no necesariamente conocida. Existe la posibilidad de crear un algoritmo de optimización del sistema propuesto a partir de un programa computacional de fácil uso e instalación.
Como resultado de este trabajo, se obtendrá un modelo matemático, el cual, traducido a un algoritmo de fácil Implantación en lenguaje C ++, ayudará al empresario a planear su producción bajo condiciones de información imperfecta.
PLANEACION ESTRATÉGICA DE LA PRODUCCIÓN
Cuando un empresario toma la determinación de invertir para producir un determinado producto o productos, es necesario tener una estrategia operacional, que guiará y especificará lo que se desea alcanzar con las operaciones que se realicen. La perspectiva de la planeación estratégica toma en consideración la planeación de la ubicación de las instalaciones, capacidad de operaciones y distribución de las áreas a largo plazo.
PLANEACIÓN DE LA CAPACIDAD
De forma general se puede definir a la capacidad operaciones como: la capacidad productiva de una instalación o volumen de producción en un periodo de tiempo.
Es por el concepto anterior que los gerentes de la producción necesitan conocer la capacidad de las instalaciones para poder suplir una demanda actual y futura del cliente.
En el ámbito productivo cuando la demanda fluctúa, los niveles de producción deseados no son los esperados. Es por eso que se debe hacer un plan de producción que proporcionara información referente a cuanto y cuando producir un determinado producto. Para lograr mejores resultados en cuanto al establecimiento de la capacidad es necesario conocer información histórica de la tendencia del consumo o adquisición del o los productos que se pretende producir, para poder hacer proyecciones de lo que podrá ser en el futuro la demanda.
Metas de la Planeación Agregada
La Planeación Agregada pretende cumplir y solventar ciertas metas:
Una de las metas a perseguir es la de proporcionar niveles aceptables de producción, inventarios y pedidos pendientes que han sido establecidos con anterioridad en un programa mayor a largo plazo.
La segunda meta a alcanzar por parte de la planeación agregada es la de optimizar la utilización de las instalaciones, para no tener colchones de seguridad muy altos de inventarios que provocan costos adicionales que repercuten directamente al aumento del costo del producto y además subutilización de las instalaciones, maquinaria, mano de obra, etc,
Por último, se debe de tener muy en consideración la estabilidad laboral observada desde el punto de vista empleado, esta provoca inseguridad pérdida de voluntad y descontento por lo que podría producir a mediano plazo una baja oferta de mano de obra para la empresa, por otro lado si se efectúan prácticas de despidos y contrataciones muy frecuentes el costo de despido y los costos de reclutamiento, inducción y entrenamiento provocan un alza en los costos inherentes al producto.
HERRAMIENTAS PARA LA PLANIFICACIÓN DE LA CAPACIDAD
La planificación de la capacidad a largo plazo no requiere de pronósticos de demanda por un vasto periodo de tiempo. Sin embargo, la precisión de los pronósticos disminuye a medida que el horizonte de los mismos se prolonga. Además, la necesidad de prever lo que hará la competencia acrecienta la incertidumbre en los pronósticos de la demanda. Finalmente, la distribución de la demanda durante un periodo cualquiera no es uniforme: en ese tiempo pueden presentarse (y a menudo se presentan) crestas y valles de demanda. Estas realidades imponen la necesidad de usar “Colchones” de capacidad. Estas dos herramientas que se van a presentar abordan con más formalidad la incertidumbre y variabilidad de la demanda: los modelos de fila de espera y los árboles de decisiones. Los modelos de fila de espera toman en cuenta el comportamiento independiente y aleatorio de muchos consumidores, tanto en sus tiempos de llegada como en sus necesidades de procesamiento. Los árboles de decisiones permiten pronosticar ciertos eventos, como las actividades de la competencia.
MODELOS DE FILA DE ESPERA
Con frecuencia, los modelos de fila de espera son útiles para la planificación de la capacidad. Frente a ciertos centros de trabajo, como el mostrador de pasajes en un aeropuerto, un centro de maquinas o una computadora central, tienden a formarse filas de espera. Es así por lo que los tiempos de llegada entre dos trabajos o clientes sucesivos varían y el tiempo de procesamiento también varia de un consumidor al siguiente: los modelos de fila de espera usan distribuciones de probabilidad para ofrecer estimaciones del tiempo de retraso promedio de los clientes, la longitud promedio de las filas de espera y la utilización del centro de trabajo. Los gerentes suelen usar estar informan para elegir la capacidad mas efectiva en términos de costos, han llamado un equilibrio entre el servicio al cliente y el costo de la capacidad agregada.
El suplemento modelos de fila de espera ofrece una exposición mas completa de las filas de espera. Allí se presentan formulas para estimar varias características importantes de un afila de espera, como el tiempo de espera promedio del consumidor y la utilización promedio de la instalación para diferentes diseños de instalaciones. Por ejemplo, una instalación puede estar diseñada para que se forme una o varias filas de espera en cada operación, y de modo que los consumidores circulen por una o múltiples operaciones. Dadas las capacidades de estas formulas y estimaciones de costos para hacer evaluaciones de tiempos de espera y de ocio, los gerentes pueden seleccionar diseños efectivos en términos de costos y niveles de capacidad que también proporcionen el nivel deseado de servicio al cliente. Para los problemas de fila de espera más complejos se requiere un análisis mediante simulación.
ÁRBOLES DE DECISIONES
Un árbol de decisiones suele ser especialmente valioso para evaluar alternativas de expansión de la capacidad cuando la demanda es incierta y cuando intervienen decisiones secuenciales en el proceso, por ejemplo. La dueña del Grandmonther's Chicken Restaurant puede ampliar ahora el restaurante, para descubrir en el cuarto año que el crecimiento de la demanda es mucho mayor de los pronosticado. En este caso, ella tendrá que decidir si debe expandirse más. En términos de costos de construcción y tiempo de inactividad, es probable que dos ampliaciones sean mucho más costosas que la construcción completa de una instalación grande. Sin embargo, hacer una ampliación grande ahora que el crecimiento de la demanda es bajo significa una utilización también baja de las instalaciones .
La figura muestra un árbol de decisiones para esta visión particular del problema y aportar nueva información. El crecimiento de la demanda solo puede ser alto o bajo, con probabilidades de 0.4 y 0.6, respectivamente. La expansión inicial en el primer año (nodo cuadrado 1) solo puede ser pequeña o grande. El segundo nodo de decisión (nodo cuadrado 2), correspondiente a si se debe de hacer o no una ampliación en alguna fecha posterior, se alcanza solamente si la expansión inicial es pequeña y la demanda resulta ser alta. Si la demanda es alta y la expansión inicial fue pequeña, se deberá tomar una decisión acerca de una posible segunda ampliación en el cuarto año. Se estiman los réditos para cada rama del árbol. Por ejemplo, si la expansión inicial es grande, el beneficio económico es de $40,000 o $220,000 , dependiendo de si la demanda es baja o alta. Al ponderar esos réditos de acuerdo con las probabilidades, se obtiene un valor esperado de $148,000. Como este rédito esperado es mayor que el rédito de $109,000 correspondiente a la pequeña expansión inicial, la mejor decisión es hacer una ampliación grande en el primer año.
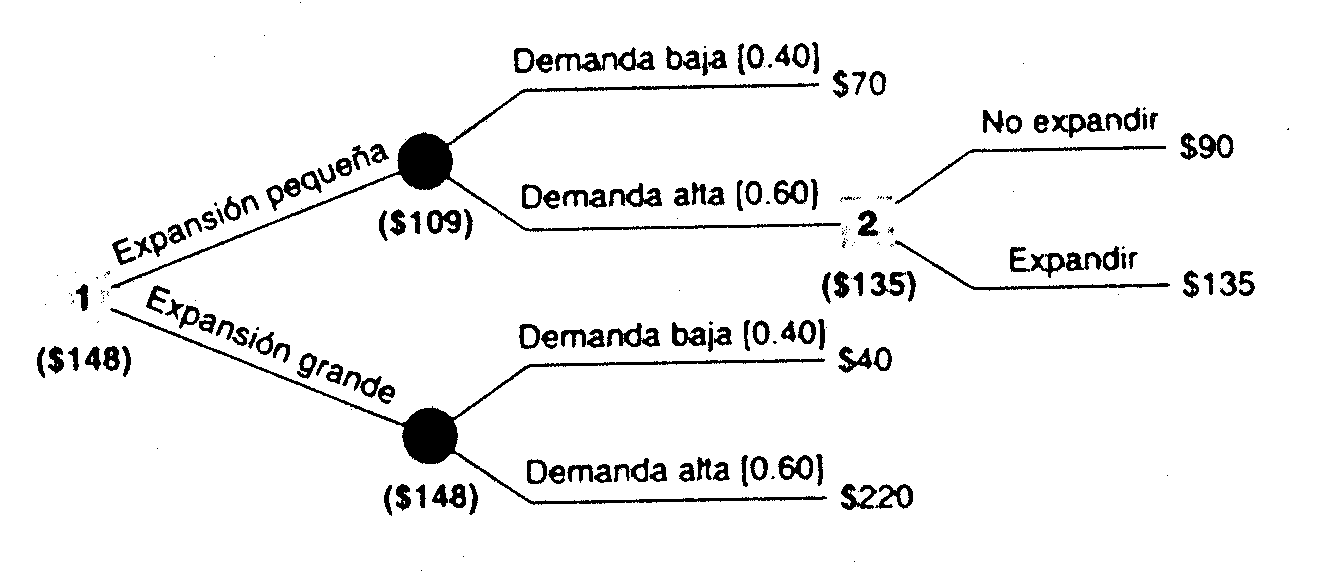
ARBOL DE DECISIONES PARA LA EXPANSION DE LA CAPACIDAD
( RETIROS EN MILES DE DOLARES )
ESTRATEGIAS PARA EL DESARROLLO DE PLANES AGREGADOS
Existen diversas formas de desarrollar planes agregados, entre los enfoques a estudiar se tienen los de hojas de cálculo y los métodos cuantitativos, dentro de los métodos de hoja de calculo están: Plan de inventario Cero, Plan de Trabajo Nivelada y Planes Mixtos; y entre los métodos cuantitativos están: Enfoque de Programación Lineal y Modelos de Transporte y otros métodos.
1- PLAN DE INVENTARIO CERO.
Este plan de consiste en producir exactamente lo que se necesita en el mes, teniendo un nivel de inventario cero; para tal efecto en los meses en que haya un descenso de demanda se tiene que hacer despidos de personal y por otro lado cuando haya aumentos en los niveles de demanda se realizaran nuevas contrataciones, para calcular el número de trabajadores necesarios para producir la demanda del mes se tiene que:
![]()
Para visualizar la resolución del método se desarrollará un ejemplo:
Randolf, Co. Produce una diversidad de productos similares de recipientes de plástico que se pueden considerar como, aunque los materiales y los tiempos de fabricación son distintos para cada producto, se puede considerar como producto agregado cada recipiente de plástico y los pronósticos para el próximo semestre serán de la siguiente forma.
| Mes | Enero | Febrero | Marzo | Abril | Mayo | Junio | Total |
| Demanda | 3091 | 3718 | 4446 | 3964 | 3562 | 3248 | 22,029 |
El año anterior se fabricaron 46,349 cajas de distintos modelos. Solamente se trabajaron 265 días y se tuvo un promedio de 42 trabajadores por lo que un trabajador en promedio puede hacer
![]()
![]()
4.16 " 5 cajas/ días-trabajador.
Además se debe considerar que una unidad producida y no vendida se considera como inventario, que también se considerará como inventario promedio mensual. El costo de mantener el inventario de fin de mes es de $ 6 por caja por mes. A principio de cada mes se pueden contratar trabajadores a un costo de $475 por trabajador. Los trabajadores actuales se pueden despedir a un costo de $625 por trabajador. Los salarios para un trabajador son de $18.50 por hora, pero a todos se les paga 8 horas de trabajo al día ($18.50/hora x 8 horas / día = $148 /día). En este momento se cuenta con 38 trabajadores.
| PLAN DE INVENTARIO CERO |
|
|
|
|
|
|
|
|
|
|
|
|
| Enero | Febrero | Marzo | Abril | Mayo | Junio | Total |
| 1 | Días | 22 | 21 | 24 | 22 | 21 | 23 | 133 |
| 2 | Unidades / Trabajador | 110 | 105 | 120 | 110 | 105 | 115 | 665 |
| 3 | Demanda | 3091 | 3718 | 4446 | 3964 | 3562 | 3248 | 22029 |
| 4 | Trabajadores necesarios | 29 | 36 | 38 | 37 | 34 | 29 | 203 |
| 5 | Trabajadores disponibles | 38 | 29 | 36 | 38 | 37 | 34 | 212 |
| 6 | Trabajadores contratados | 0 | 6 | 0 | 0 | 0 | 0 | 6 |
| 7 | Costo de contratación | 0 | 2850 | 0 | 0 | 0 | 0 | 2850 |
| 8 | Trabajadores despedidos | 7 | 0 | 2 | 1 | 3 | 5 | 18 |
| 9 | Costo de despedidos | 4375 | 0 | 0 | 0 | 0 | 0 | 4375 |
| 10 | Trabajadores empleados | 29 | 36 | 38 | 37 | 34 | 29 | 203 |
| 11 | Costo de mano de obra | 94424 | 111888 | 134976 | 120472 | 105672 | 98716 | 666148 |
| 12 | Unidades producidas | 3091 | 3718 | 4446 | 3964 | 3562 | 3248 | 22029 |
| 13 | Inventario Neto | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | Costo de almacenaje | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | Costo de ordenes atrasadas |
|
|
|
|
|
|
|
| 16 | Costo total | $98,799.00 | $114,738.00 | $134,976.00 | $120,472.00 | $105,672.00 | $98,716.00 | $673,373.00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Unidades/ día-trabajador = | 5 |
|
|
|
|
|
|
|
| Costo de contratación = | $ 475 |
|
|
|
|
|
|
|
| Costo de despido = | $ 625 |
|
|
|
|
|
|
|
| Salario = | $ 148 |
|
|
|
|
|
|
|
| Costo de almacenaje = | $ 6 |
|
|
|
|
|
|
|
| Trabajadores disponibles = | 38 |
|
|
|
|
|
|
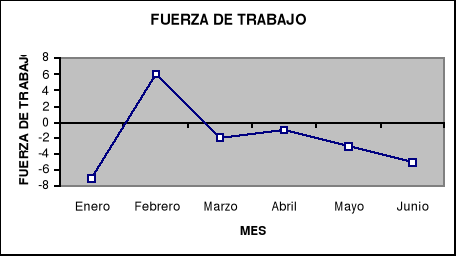
Tal como se muestra en la siguiente gráfica en que se muestra la variabilidad de la fuerza de trabajo, en esta se puede observar claramente como se comporta por efecto del plan de inventario cero, registrándose contrataciones y despidos según la demanda, este fenómeno no es muy deseado.
2- PLAN DE FUERZA DE TRABAJO NIVELADA.
Este plan usa el inventario producido en los periodos de baja demanda para poder satisfacer la demanda en los periodos pico y esto se logra manteniendo el mismo número de trabajadores durante todos los periodos.
Utilizando la información del ejemplo anterior se analizará el comportamiento de la producción bajo las condiciones de la fuerza laboral constante y que se muestra a continuación.
Para poder utilizar el plan de fuera de trabajo nivelada se necesita calcula que cantidad de fuerza laboral es necesario tener a lo largo de todos los periodos, cantidad que no puede ser cualquiera, porque una cantidad elevada de trabajadores produciría una gran cantidad de inventario, elevándose los costos por ese lado, por lo contrario si la fuerza laboral es baja no se podrá producir lo necesario para satisfacer las demandas de cada uno de los periodos y se generarían costos por ordenes retrasadas muy elevados además que otro proveedor podría suplir la falta de abastecimiento que sufriría el cliente por la mala planificación; por todo lo anterior es necesario calcular una cantidad de fuerza laboral que produzca lo necesario tanto para satisfacer la demanda y no generar demasiado inventario, esto se puede lograr de dos formas:
1- Mediante la formula
![]()
A través del análisis gráfico.
| FUERZA DE TRABAJO NIVELADA | |||||||||||||
|
|
|
|
|
|
|
|
|
| |||||
|
|
| Enero | Febrero | Marzo | Abril | Mayo | Junio | Total | |||||
| 1 | Días | 22 | 21 | 24 | 22 | 21 | 23 | 133 | |||||
| 2 | Unidades / Trabajador | 110 | 105 | 120 | 110 | 105 | 115 | 665 | |||||
| 3 | Demanda | 3091 | 3718 | 4446 | 3964 | 3562 | 3248 | 22029 | |||||
| 4 | Trabajadores necesarios | 34 | 34 | 34 | 34 | 34 | 34 | 204 | |||||
| 5 | Trabajadores disponibles | 38 | 34 | 34 | 34 | 34 | 34 | 208 | |||||
| 6 | Trabajadores contratados | 0 | 0 | 0 | 0 | 0 | 0 |
||||||
| Enviado por: | El Perron |
| Idioma: | castellano |
| País: | México |