Matemáticas
Operaciones con conjuntos
Operaciones con tres conjuntos
En un diagrama de Venn, las posiciones relativas de tres conjuntos pueden ser muy variadas.
% elementos que no pertenecen a ningún conjunto, excepto al universal (región gris);
% elementos que pertenecen a un solo conjunto (regiones roja, amarilla y azul);
% elementos que pertenecen a dos conjuntos (regiones anaranjada, verde y violeta); y
% elementos que pertenecen a los tres conjuntos (región marrón).
Es decir, la disposición más general es la que define ocho regiones. En ninguna otra se llega a esta cantidad. [La disposición 5, por ejemplo, tiene siete. Si los elementos de tres conjuntos pueden ser ubicados en el diagrama 5, también podrán ser ubicados en el diagrama 12: una región
Obsérvese que la cantidad de regiones de cada clase se puede calcular aplicando la fórmula siguiente:
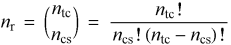
Donde ntc es el número total de conjuntos y ncs es el número de conjuntos que se solapan (superponen) en las regiones en cuestión. Por ejemplo, en un diagrama de tres conjuntos ntc = 3, la cantidad de regiones donde no hay conjuntos (ncs = 0) es 3!/[0! (3-0)!] = 1 (gris); la cantidad de regiones donde hay un solo conjunto (ncs = 1) es 3!/[1! (3-1)!] = 3 (roja, amarilla y azul); la cantidad de regiones donde se solapan dos conjuntos (ncs = 2) es 3!/[2! (3-2)!] = 3 (anaranjada, verde y violeta); y la cantidad de regiones donde se solapan los tres conjuntos (ncs = 2) es 3!/(3-3)! = 1 (marrón). El número total de regiones (colores) se puede obtener entonces aplicando la siguiente fórmula:
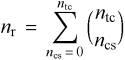
En otros términos, la cantidad de regiones surge de la construcción conocida como "Triángulo de Tartaglia". Los números de cada fila se obtienen sumando los dos adyacentes de la columna anterior
| cantidad de | cantidad de regiones | total de | |||||||||
| 0 1 2 3 | 1 1 1 1 2 1 1 3 3 1 | 1 2 4 8 | |||||||||
Este procedimiento está justificado por el hecho de que las regiones están ordenadas en una estructura jerárquica del tipo "árbol": si en una región un conjunto se solapa con otros dos, se solapa también con cada uno de ellos, y ellos se solapan entre sí. La pregunta: « ¿Cuántas regiones hay donde se superponen ncs conjuntos?» es equivalente a la pregunta: « ¿Cuántos jefes tiene un empleado que se encuentra en el nivel ncs-ésimo de una escala jerárquica como la siguiente?»
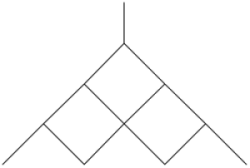
Cada jefe vale por el número de superiores que tiene.
La tabla siguiente muestra distintas formas de identificar las regiones
La última columna contiene las ternas ordenadas correspondientes a cada una de las ocho regiones. Las tres componentes indican, respectivamente, si los elementos pertenecen (1) o no (0) a los conjuntos A, B y C.
El resultado de una operación con tres conjuntos es, gráficamente, una parte del diagrama que los representa (en el caso más general, el diagrama 12 de la primera tabla). Cualquier región compuesta se puede expresar en términos de las ocho regiones elementales de la tabla anterior. En el cuadro siguiente se muestran algunos ejemplos
Sin embargo, como se observa en la notación alternativa (última columna), muchas veces es posible escribir expresiones más compactas. (Éste no es el caso de la operación 3.)
CONJUNTO INFINITO
Llamamos conjunto infinito a cualquier conjunto que puede ponerse en biyección con un subconjunto propio de sí mismo.
De la definición establecida en el apartado anterior y la definición de cardinalidad se puede justificar porque el conjunto de los números naturales N es infinito sin recurrir a un argumento de proceso ilimitado que es el que comúnmente se usa para justificar la infinitud de N.
Se puede afirmar que N es un conjunto infinito notando el hecho de que existe una función biyectiva entre N y el subconjunto de los números pares P. Basta tomar la función f : N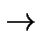
P; f(n)= 2n. Fácilmente vemos que esta función es una biyección de N en P . También se puede probar la infinitud de los naturales estableciendo una biyección entre N y el subconjunto de los números impares I.
El conjunto P es también infinito. Para ver esto basta considerar la biyección que se establece entre él y el conjunto 2P = {k 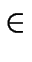
P : k = 2p;p 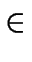
P} = P - {2} mediante la biyección h : P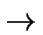
2P;h(p) = 2p.
Análogamente se demuestra que el conjunto de números impares I es también infinito asociando cada número impar i 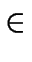
I con números de la forma i + 2, i 
I.
Ahora como Z, Q y R contienen a N, la cardinalidad de estos tres conjuntos debe ser mayor o igual que la de N y por lo tanto también son infinitos.
Descargar
| Enviado por: | Landy |
| Idioma: | castellano |
| País: | México |
