Estadística
Natalidad y mortalidad en departamento de provincia peruana
PRESENTACION
L
A Facultad de Ingeniería Estadística e Informática de la UNA-PUNO, a través de los estudiantes Apaza López, Hugo y Ruiz Condori, Elvis R. Respectivamente, en su afán de alcanzar Información consolidada de recientes estudios estadísticos presentamos el documento titulado “ANÁLISIS DE NATALIDAD Y MORTALIDAD DEL DPTO. DE PUNO EN LA PROVINCIA DE LAMPA 1991-2003”, el cual contiene información sobre modelos de tendencia para la estimación de la natalidad y la mortalidad, una estimación de la población de la provincia de Lampa de un periodo anual, estimación de la población hasta el 2005, tasa bruta de mortalidad, tendencia de la tasa bruta de mortalidad hasta el año 2005 y por ultimo conclusiones.
Esta facultad de FINESI a través de sus alumnos en forma publica hace llegar sus agradecimientos al Instituto Nacional de Estadística e Informática, por su colaboración que permite la elaboración de este documento.
FINESI-UNA-PUNO
ANALISIS DE NATALIDAD Y MORTALIDAD DE LA PROVINCIA DE LAMPA
1° Realizar los modelos de tendencia para la estimación de la natalidad y mortalidad.
Modelos de tendencia para la estimación de la natalidad y mortalidad
Para el Análisis de la tendencia de los datos referente a la natalidad y mortalidad se propone usar ecuaciones de regresión de acuerdo a la dirección de los puntos en el diagrama de dispersión. La que muestra la mayor coeficiente de correlación será la de mejor ajuste y por consiguiente nuestra ecuación definitiva de estimación elegiremos, para selecciona nuestro modelo adecuado observaremos las diferentes nubes de puntos lo que nos ayudara ha elegir el modelo adecuado.
A continuación mostramos nuestra tabla: de nacimiento, mortalidad y población total clasificados según años anuales lo que nos ayudara para mostrar los gráficos.
| Año | Nacimiento | Mortalidad | Población Total | X |
| 1991 | 514 | 42732 | 0 | |
| 1992 | 414 | 43097 | 1 | |
| 1993 | 1185 | 492 | 43461 | 2 |
| 1994 | 1313 | 430 | 44926 | 3 |
| 1995 | 1196 | 458 | 45150 | 4 |
| 1996 | 1126 | 401 | 45083 | 5 |
| 1997 | 972 | 366 | 45458 | 6 |
| 1998 | 1029 | 360 | 45620 | 7 |
| 1999 | 950 | 351 | 46429 | 8 |
| 2000 | 896 | 332 | 46871 | 09 |
| 2001 | 843 | 313 | 47313 | 10 |
| 2002 | 789 | 295 | 47754 | 11 |
| 2003 | 735 | 276 | 48196 | 12 |
FUENTE: INEI. Nacimiento, Mortalidad y Población total
de la provincia de LAMPA
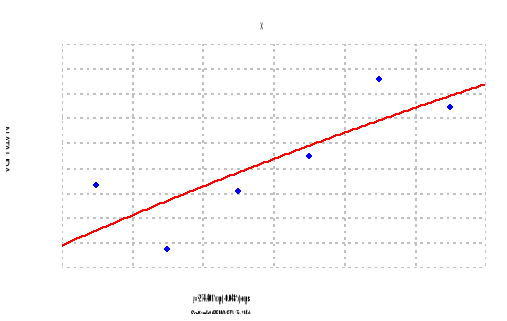
Diagrama de dispersión regresionados en el software estadístico “STATISTICA” de las variables: natalidad en función de los años anuales (0,1,2,3,4,5,6,..). Según sus gráficos de los modelos: lineal, exponencial, polinomial, etc. Con sus respectivos coeficientes de correlación.
Diagrama de dispersión de datos para la NATALIDAD en la provincia de Lampa.
Diagrama de dispersión regresionados en al paquete “STATISTICA” de las siguientes variables: NATALIDAD en función de los años anuales (0,1,2,3,4,5...).
MODELO DE CRECIMIENTO LINEAL:
Es un modelo en el que se incrementa la población de forma aritmética; esta basado mínima menta en las cifras para dos censos o periodos.
Su ecuación es la siguiente:
Donde:
n :Periodo de proyección
t :Fecha de observación del primer censo
t+k :Fecha del segundo censo
t+k+n :Fecha de la poblacion a proyectar
Pt :Población del primer censo
Pt+k :Ppoblacion del segundo censo
Pt+k+n :Poblacion a proyectar
K :Periodo transcurrido entra dos periodos.
Y=1.079*E5-53.514(X) con un R=0.148679998
MODELO LOGARÍTMICA:
Y=8.125-2.459LOG(X) con un R=0.149358628
MODELO EXPONENCIAL
Y=1274.401EXP(-0.048X) con un R=0.148431667
MODELO POLINOMIAL
Este modelo requiere de tres o mas censos o periodos como en nuestro caso, gráficamente tiene forma de ciclos los que son en el numero n-1 del grado n de la ecuación; el modelo general se muestra ha continuación:
donde:
X :Periodo intercensal observado desde el primer curso
a0 +a1+ a2 +a3 + a4 + a5 +....+ an constante de regresión
simbolización de los periodos intercensales con sus respectivas poblaciones.
| X | Px |
| 1 | P0 |
| 2 | P1 |
| 3 | P2 |
Para:
n =1 entonces
n =1 entonces
n =1 entonces ![]()
Observando la nube de puntos, se ajusta regularmente al modelo polinomial en comparación con las anteriores. Por ejemplo lo puntos (1995,1196) y (1996,1126) se encuentran postrados sobre la mismísima línea. Según su coeficiente de correlacion que esta alto en comparación de otras cuyo modelo estimado es el siguiente:
Y = -3.568 + 35814.19X - 8.987X2 con un R=0.83763
Observando la nube de puntos el modelo Polinomial se ajusta regularmente porque tiene un R alto para lo cual seria nuestra solución adecuada en cuanto a NACIMIENTOS en la Prov. de Lampa.
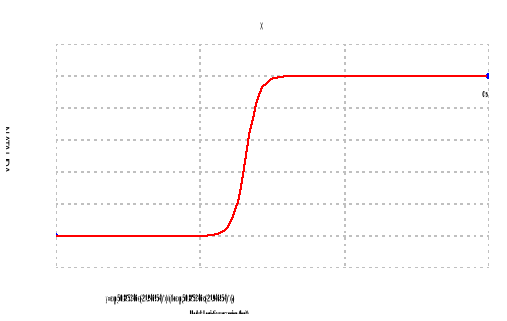
MODELO LOGISTICO O CURVA LOGÍSTICA
este modelo es usado con la hipótesis de que al aumentar la población, tiende a disminuir su tasa de crecimiento debido a factores represivos. Su ecuación es:
El software estadístico “STATISTICA”muestra el siguiente grafico:
MORTALIDAD
Diagrama de dispersión de datos para la MORTALIDAD en la provincia de Lampa.
Diagrama de dispersión regresionados en al paquete “STATISTICA” de las siguientes variables: mortalidad en función de los años anuales (0,1,2,3,4,5,...).
MODELO DE CRECIMIENTO LINEAL:
Es un modelo en el que se incrementa la población de forma aritmética; esta basado mínima menta en las cifras para dos censos o periodos.
Su ecuación es la siguiente:
Donde:
n :Periodo de proyección
t :Fecha de observación del primer censo
t+k :Fecha del segundo censo
t+k+n :Fecha de la poblacion a proyectar
Pt :Población del primer censo
Pt+k :Ppoblacion del segundo censo
Pt+k+n :Poblacion a proyectar
K :Periodo transcurrido entra dos periodos.
Y=37541.32-18.607(X) con un R=0.81721527
MODELO LOGARÍTMICA:
Y=2.824*e5+85447.273LOG(X) con un R=0.91322
MODELO EXPONENCIAL
Y=496.443EXP(-0.044*X) con un R=--------(no muestra nada)
MODELO POLINOMIAL
Este modelo requiere de tres o mas censos o periodos como en nuestro caso, gráficamente tiene forma de ciclos los que son en el numero n-1 del grado n de la ecuación; el modelo general se muestra ha continuación:
donde:
X :Periodo intercensal observado desde el primer curso
a0 +a1+ a2 +a3 + a4 + a5 +....+ an constante de regresión
simbolización de los periodos intercensales con sus respectivas poblaciones.
| X | Px |
| 1 | P0 |
| 2 | P1 |
| 3 | P2 |
Para:
n =1 entonces
n =1 entonces
n =1 entonces ![]()
Observando la nube de puntos, se ajusta regularmente al modelo polinomial en comparación con las anteriores. Por ejemplo lo puntos (1995,1196) y (1996,1126) se encuentran postrados sobre la mismísima línea. Según su coeficiente de correlación que esta alto en comparación de otras cuyo modelo estimado es el siguiente:
Y = 485.292-9.399X - 1.315X2 con un R=0.91685
Observando la nube de puntos el modelo Polinomial se ajusta regularmente porque tiene un R alto en comparación del modelo logarítmico para lo cual seria nuestra solución adecuada en cuanto a MORTALIDAD en la Prov. de Lampa.
MODELO LOGISTICO O CURVA LOGÍSTICA
este modelo es usado con la hipótesis de que al aumentar la población, tiende a disminuir su tasa de crecimiento debido a factores represivos. Su ecuación es:
El software estadístico “STATISTICA”muestra el siguiente grafico:
Como hemos podido ver en nuestro diagrama de dispersión de nube de punto hemos podido notar la presencia de un decrecimiento de la población lo cual podemos deducir que nos encontramos en un modelo Polinomial en ambos casos tanto para Natalidad y Mortalidad. Porque muestra un coeficiente de correlación bastante alto y eficiente (cercano a 1).
2° Realizar la estimación de la población de la provincia de Lampa de un periodo interanual.
La población absoluta para los años anuales serán estimados con el polinomio de NEWTON- METODO DE LAS DIFERENCIAS DIVIDIDAS , la tabla de NEVILLE-AITKEN es la siguiente:
Diferencias divididas de Neville-Aitken entre periodos interanuales para calcular el polinomio de interpolación de población de la provincia de Lampa.
| fecha anual | xi | f(xi) | f(xi,xi+1) | f(xi,xi+1,xi+2) | f(xi,xi+1,xi+2,xi+3) | f(xi,xi+1,xi+2,xi+3,xi+4) | f(xi,xi+1,xi+2,xi+3,xi+4,xi+5) | f(xi,xi+1,xi+2,xi+3,xi+4,xi+5,xi+6) |
| 1993 | 16.01 | 43461 |
|
|
|
|
|
|
|
|
|
| 369.018 |
|
|
|
|
|
| 1994 | 19.98 | 44926 |
| -1165.5131 |
|
|
|
|
|
|
|
| -62.2222 |
| 2957.631192 |
|
|
|
| 1995 | 16.38 | 45150 |
| -71.189579 |
| -50102.46783 |
|
|
|
|
|
| 216.129 |
| -48.5168776 |
| -19041.63634 |
|
| 1996 | 16.07 | 45083 |
| 118.51141 |
| -22.96424201 |
| -14511.0881 |
|
|
|
| -139.405 |
| 103.0471197 |
| -32.06807155 |
|
| 1997 | 13.38 | 45458 |
| -190.62995 |
| 146.6758565 |
|
|
|
|
|
| 123.664 |
| -144.835078 |
|
|
|
| 1998 | 14.69 | 45620 |
| 9.2424605 |
|
|
|
|
El polinomio general deducido de la fórmula de Newton es:
F(x)= -2920.91-16286.1(X1)-51337.2 (X2)+13918.58( X3)-1346.12 (X4)+56.77751(X5)- 0.886708(X1)
La interpolación de la población para las fechas anuales nos demuestra que este polinomio es eficiente con estimaciones de punto tal y como se demuestra en la tabla siguiente:
| fecha anual | xi | Yi | Yi estimada |
| 1993 | 16.01 | 43461 | 44421.9662 |
| 1994 | 19.98 | 44926 | 45546.1086 |
| 1995 | 16.38 | 45150 | 45525.182 |
| 1996 | 16.07 | 45083 | 44540.751 |
| 1997 | 13.38 | 45458 | 45581.9742 |
| 1998 | 14.69 | 45620 | 45785.8393 |
3° Realizar la estimación de la población media hasta el año 2005.
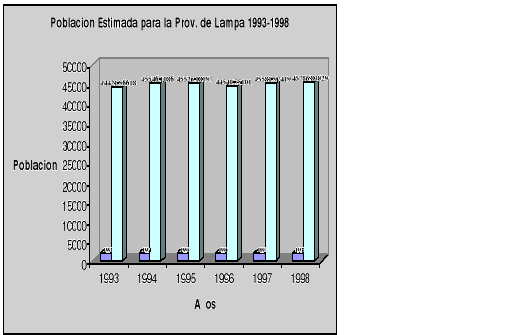
La poblacio para la prov. De Lampa estimada para cada 30 de junio de los años de 1999 al 2005 fue, obtenida con el polinomio determinado en la pregunta N° 2.
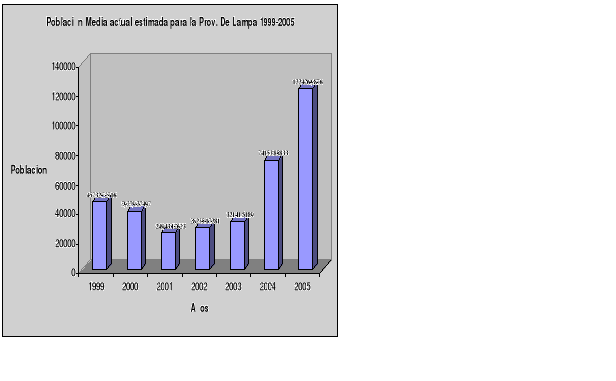
Población media actual estimada para la Prov. De Lampa
| Año | x | Población Estimada |
| 1999 | 13.41402 | 45732.72716 |
| 2000 | 12.65088 | 39279.27497 |
| 2001 | 11.88774 | 24943.12623 |
| 2002 | 11.1246 | 28235.17281 |
| 2003 | 10.36146 | 32141.5189 |
| 2004 | 9.59832 | 74153.85833 |
| 2005 | 8.83518 | 122426.9876 |
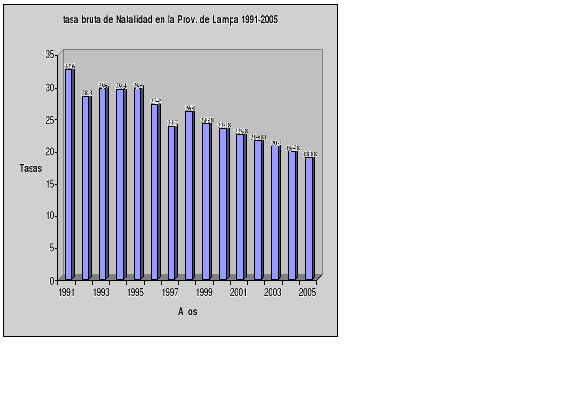
4° Calcular la tasa bruta de Natalidad
| Año | N (o/oo) |
| 1991 | 32.6 |
| 1992 | 28.3 |
| 1993 | 29.7 |
| 1994 | 29.4 |
| 1995 | 29.7 |
| 1996 | 27.2 |
| 1997 | 23.7 |
| 1998 | 26.1 |
| 1999 | 24.28 |
| 2000 | 23.38 |
| 2001 | 22.48 |
| 2002 | 21.581 |
| 2003 | 20.7 |
| 2004 | 19.78 |
| 2005 | 18.88 |
Se observa que para el periodo de estudio la tendencia de la tasa bruta de natalidad es decreciente, donde para el año 1991 se tuvo aproximadamente 32 nacimientos de cada 1000 personas y así respectivamente. El descenso se puede atribuir al despoblamiento por efectos de la sequía, falta de empleo, subdesarrollo, emigración de sus habitantes.
En resumen la tendencia decreciente de la natalidad, se puede atribuir a los siguientes factores :
Aplicación de programas de planificación familiar.
Emigración de la población en edad de procrear.
Sequía, subdesarrollo , otros.
5° Calcular la tendencia de la tasa bruta de natalidad hasta el 2005.
Puesto que la tasa bruta de natalidad sigue una tendencia decreciente se opta por realizar el ajuste por las ecuaciones lineal, exponencial y polinomial de segundo y tercer grado. Las ecuaciones y sus coeficientes de correlación se muestran en la tabla.
Ecuaciones de regresión para la tendencia de la tasa bruta de natalidad.
| modelo | ecuación | R |
| lineal simple | Y = 31.13333 - 0.66000X | 0.68119 |
| exponencial | Y = (31.16804)( 0.22525)x | 0.68323 |
| polinomio de segundo grado | Y = 31.40714 - 1.07071X+0.82143X2 | 0.69235 |
| polinomio de tercer grado | Y = 32.39603 - 5.58664X+2.554365X2-0.329630X3 | 0.95285 |
Valores estimados para la tasa bruta de Natalidad según la ecuación de tendencia
|
| Estimación mediante ecuación de tendencia | |||||
| año | X | Tasa bruta de natalidad | lineal | expon | pol2* | pol3* |
| 1999 | 0 | 24.28 | 31.13333 | 31.16804 | 31.40714 | 32.39603 |
| 2000 | 1 | 23.38 | 30.47333 | 7.02060101 | 31.15786 | 29.034125 |
| 2001 | 2 | 22.48 | 29.81333 | 1.58139038 | 32.55144 | 28.80317 |
| 2002 | 3 | 21.581 | 29.15333 | 0.35620818 | 35.58788 | 29.725385 |
| 2003 | 4 | 20.7 | 28.49333 | 0.08023589 | 40.26718 | 29.82299 |
| 2004 | 5 | 19.78 | 27.83333 | 0.01807313 | 46.58934 | 27.118205 |
| 2005 | 6 | 18.88 | 27.17333 | 0.00407097 | 54.55436 | 19.63325 |
Las estimaciones mas cercanas a las tasas brutas de natalidad observadas para el periodo de 1999-2005 son las que se obtienen con la ecuación de mas alto coeficiente de correlación, sin embargo para realizar proyecciones las ecuaciones exponencial, lineal, y polinómica de grado 2 dan tasas con un descenso y un crecimiento acelerado volviéndose inexactas por lo que recomendamos la ecuación polinómica de grado 3 porque se asemejan as a la realidad.
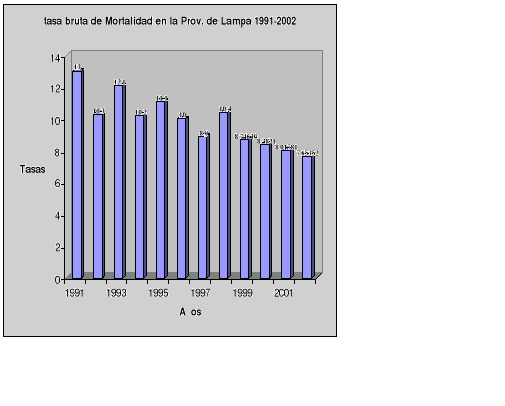
6° Calcular la tasa bruta de Mortalidad
| Año | M (o/oo) |
| 1991 | 13 |
| 1992 | 10.3 |
| 1993 | 12.1 |
| 1994 | 10.2 |
| 1995 | 11.1 |
| 1996 | 10 |
| 1997 | 8.9 |
| 1998 | 10.4 |
| 1999 | 8.74639 |
| 2000 | 8.3821 |
| 2001 | 8.01781 |
| 2002 | 7.65352 |
| 2003 | 7.28923 |
| 2004 | 6.92494 |
| 2005 | 6.56065 |
Se observa que para el periodo de estudio la tendencia de la tasa bruta de Mortalidad es decreciente, donde para el año 1991 se tuvo aproximadamente 13 defunciones de cada 1000 personas y así respectivamente. El descenso se puede atribuir a muertes de personas ancianas, personas con enfermedades como: neumonía, tuberculosis, etc y las muertes causadas por accidentes de transito.
7° Calcular la tendencia de la tasa bruta de Mortalidad hasta el 2005.
Puesto que la tasa bruta de Mortalidad sigue una tendencia decreciente se opta por realizar el ajuste por las ecuaciones lineal, exponencial y polinomial de segundo y tercer grado. Las ecuaciones y sus coeficientes de correlación se muestran en la tabla.
Ecuaciones de regresión para la tendencia de la tasa bruta de Mortalidad.
| modelo | ecuación | R |
| lineal simple | Y = = 12.025 -0.36428631X | 0.69257 |
| exponencial | Y =(12.09645)*(0.96596)x | 0.70010 |
| polinomio de segundo grado | Y = = 12.45-0.789286X+0.060714X2 | 0.73003 |
| polinomio de tercer grado | Y = 32.39603 - 5.58664X+2.554365X2-0.329630X3 | 0.73018 |
Valores estimados para la tasa bruta de Mortalidad según la ecuación de tendencia
|
| Estimación mediante ecuación de tendencia | |||||
| año | X | Tasa bruta de Mortalidad | lineal | expon | pol2* | pol3* |
| 1999 | 0 | 8.74639 | 12.025 | 12.09645 | 12.45 | 12.42879 |
| 2000 | 1 | 8.3821 | 11.6607137 | 11.6846868 | 11.721428 | 11.736582 |
| 2001 | 2 | 8.01781 | 11.2964274 | 11.2869401 | 11.114284 | 11.135498 |
| 2002 | 3 | 7.65352 | 10.9321411 | 10.9027327 | 10.628568 | 10.637658 |
| 2003 | 4 | 7.28923 | 10.5678548 | 10.5316036 | 10.26428 | 10.255182 |
| 2004 | 5 | 6.92494 | 10.2035685 | 10.1731079 | 10.02142 | 10.00019 |
| 2005 | 6 | 6.56065 | 9.83928214 | 9.82681526 | 9.899988 | 9.884802 |
Las estimaciones mas cercanas a las tasas brutas de Mortalidad observadas para el periodo de 1999-2005 son las que se obtienen con la ecuación de mas alto coeficiente de correlación, sin embargo para realizar proyecciones las ecuaciones exponencial, lineal y polinómica de grado 2 dan tasas con un descenso y un crecimiento acelerado volviéndose inexactas por lo que recomendamos utilizar ecuación polinómica de grado 3 porque se asemejan al menos a la realidad.
CONCLUSIONES.
D
e acuerdo a nuestro análisis mostrado concluimos que en la provincia de lampa exista un balanceo entre las tasas de natalidad y mortalidad, para lo cual podemos predecir que para años posteriores la Prov. de Lampa se encuentre menos poblada por razones de emigración a otras ciudades como son Juliaca , Puno, Arequipa, etc. Y que la Población en edad de Fecundidad será menos por tales razones ya mencionados.
1
Descargar
| Enviado por: | EyH |
| Idioma: | castellano |
| País: | Perú |
