Estadística
Muestreo estadístico
Estudio estadístico.
Relación talla de calzado
Y
altura física.
VARIABLE X: Número de calzado de los encuestados.
VARIABLE Y: Altura de los encuestados.
ÍNDICE
Tabla de datos de los encuestados 2-3
Cálculo de media de la variable X y comentario 4
Cálculo de la varianza de la variable X 4
Cálculo de la desviación típica de la variable X 4
Representación gráfica de valores y frecuencia de la variable X 4
Cálculo de media de la variable Y, y comentario 5
Cálculo de la varianza de la variable Y 5
Cálculo de la desviación típica de la variable Y 5
Representación gráfica de valores y frecuencia de la variable Y 5
Cálculo de la covarianza de la variable bidimensional (X, Y) 6
Diagrama de dispersión de la variable (X, Y) 6
Coeficiente de correlación de la variable (X, Y) 6
Cálculo de la recta de regresión de la variable X sobre la variable Y 7
Cálculo de la recta de regresión de la variable Y sobre la variable X 7
Predicción de 5 valores de la variable X, a partir de 5 valores de Y 7-8
Predicción de 5 valores de la variable Y, a partir de 5 valores de X 8-9
Comentario sobre las conclusiones del estudio realizado
Tabla de datos de los encuestados
| ALTURA (metros) | Nº DE PIE | ||
| 1 | 1,80 | 44 | |
| 2 | 1,80 | 42 | |
| 3 | 1,82 | 47 | |
| 4 | 1,90 | 44 | |
| 5 | 1,70 | 42 | |
| 6 | 1,82 | 45 | |
| 7 | 1,75 | 42 | |
| 8 | 1,78 | 44 | |
| 9 | 1,71 | 42 | |
| 10 | 1,81 | 42 | |
| 11 | 1,82 | 46 | |
| 12 | 1,71 | 41 | |
| 13 | 1,74 | 43 | |
| 14 | 1,80 | 44 | |
| 15 | 1,79 | 44 | |
| 16 | 1,78 | 45 | |
| 17 | 1,80 | 42 | |
| 18 | 1,80 | 44 | |
| 19 | 1,78 | 43 | |
| 20 | 1,76 | 42 | |
| 21 | 1,70 | 40 | |
| 22 | 1,65 | 41 | |
| 23 | 1,71 | 40 | |
| 24 | 1,77 | 47 | |
| 25 | 1,89 | 46 | |
| 26 | 1,73 | 41 | |
| 27 | 1,78 | 44 | |
| 28 | 1,80 | 44 | |
| 29 | 1,76 | 40 | |
| 30 | 1,72 | 42 | |
| 31 | 1,70 | 42 | |
| 32 | 1,76 | 42 | |
| 33 | 1,73 | 42 | |
| 34 | 1,73 | 42 | |
| 35 | 1,74 | 42 | |
| 36 | 1,80 | 42 | |
| 37 | 1,72 | 38 | |
| 38 | 1,80 | 42 | |
| 39 | 1,73 | 41 | |
| 40 | 1,91 | 44 | |
| Xi | Yi | ni | Xi·ni | Yi·ni | Xi2·ni | Yi2·ni | Xi·Yi·ni |
| 1,65 | 41 | 1 | 1,65 | 41 | 2,7225 | 1681 | 67,65 |
| 1,7 | 42 | 2 | 3,4 | 84 | 5,78 | 3528 | 142,8 |
| 1,7 | 40 | 1 | 1,7 | 40 | 2,89 | 1600 | 68 |
| 1,71 | 40 | 1 | 1,71 | 40 | 2,9241 | 1600 | 68,4 |
| 1,71 | 41 | 1 | 1,71 | 41 | 2,9241 | 1681 | 70,11 |
| 1,71 | 42 | 1 | 1,71 | 42 | 2,9241 | 1764 | 71,82 |
| 1,72 | 38 | 1 | 1,72 | 38 | 2,9584 | 1444 | 65,36 |
| 1,72 | 42 | 1 | 1,72 | 42 | 2,9584 | 1764 | 72,24 |
| 1,73 | 41 | 2 | 3,46 | 82 | 5,9858 | 3362 | 141,86 |
| 1,73 | 42 | 2 | 3,46 | 84 | 5,9858 | 3528 | 145,32 |
| 1,74 | 42 | 1 | 1,74 | 42 | 3,0276 | 1764 | 73,08 |
| 1,74 | 43 | 1 | 1,74 | 43 | 3,0276 | 1849 | 74,82 |
| 1,75 | 42 | 1 | 1,75 | 42 | 3,0625 | 1764 | 73,5 |
| 1,76 | 40 | 1 | 1,76 | 40 | 3,0976 | 1600 | 70,4 |
| 1,76 | 42 | 2 | 3,52 | 84 | 6,1952 | 3528 | 147,84 |
| 1,77 | 47 | 1 | 1,77 | 47 | 3,1329 | 2209 | 83,19 |
| 1,78 | 43 | 1 | 1,78 | 43 | 3,1684 | 1849 | 76,54 |
| 1,78 | 44 | 2 | 3,56 | 88 | 6,3368 | 3872 | 156,64 |
| 1,78 | 45 | 1 | 1,78 | 45 | 3,1684 | 2025 | 80,1 |
| 1,79 | 44 | 1 | 1,79 | 44 | 3,2041 | 1936 | 78,76 |
| 1,8 | 42 | 4 | 7,2 | 168 | 12,96 | 7056 | 302,4 |
| 1,8 | 44 | 4 | 7,2 | 176 | 12,96 | 7744 | 316,8 |
| 1,81 | 42 | 1 | 1,81 | 42 | 3,2761 | 1764 | 76,02 |
| 1,82 | 45 | 1 | 1,82 | 45 | 3,3124 | 2025 | 81,9 |
| 1,82 | 46 | 1 | 1,82 | 46 | 3,3124 | 2116 | 83,72 |
| 1,82 | 47 | 1 | 1,82 | 47 | 3,3124 | 2209 | 85,54 |
| 1,89 | 46 | 1 | 1,89 | 46 | 3,5721 | 2116 | 86,94 |
| 1,9 | 44 | 1 | 1,9 | 44 | 3,61 | 1936 | 83,6 |
| 1,91 | 44 | 1 | 1,91 | 44 | 3,6481 | 1936 | 84,04 |
| 40 | 70,8 | 1710 | 125,4378 | 73250 | 3029,39 |
Cálculo de media de la variable X y comentario
![]()
Mediante este cálculo se obtiene que la altura media de los 40 estudiantes de edades comprendidas entre 16 y 18 años de la ciudad de Jaén encuestados es de 1,77 metros. No es una altura muy elevada ya que hay varias personas relativamente bajas y esto hace que la media de altura disminuya considerablemente.
Cálculo de la varianza de la variable X
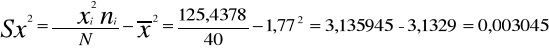
Cálculo de la desviación típica de la variable X
![]()
Representación gráfica de valores/ frecuencia de la variable X
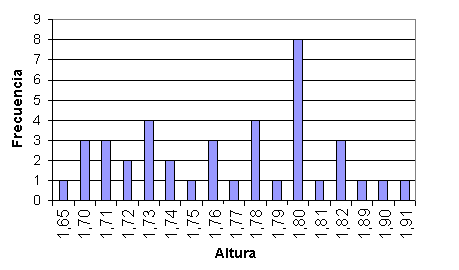
Cálculo de media de la variable Y y comentario
![]()
El resultado obtenido en esta operación expresa que los estudiantes de Jaén, comprendidos entre los 16 hasta los 18 años, usan una talla media de un 42,75. Es una talla considerable entre los adolescentes de hoy en día.
Cálculo de la varianza de la variable Y
Cálculo de la desviación típica de la variable Y
Representación gráfica de valores/ frecuencia de la variable Y
Cálculo de la covarianza de la variable bidimensional (X, Y)
Diagrama de dispersión de la variable (X, Y)
Coeficiente de correlación de la variable (X, Y)
Cálculo de la recta de regresión de X sobre Y
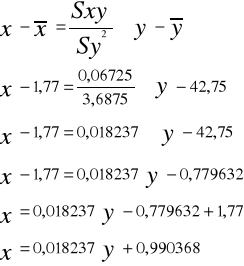
Cálculo de la recta de regresión de Y sobre X
Predicción de 5 valores de X, a partir de 5 valores de Y
![]()
Predicción de 5 valores de Y, a partir de 5 valores de X
![]()
Comentario sobre las conclusiones del estudio realizado
Este trabajo esta desarrollado a partir de individuos comprendidos entre 16 y 18 años. Encuestando a 40 personas sobre su altura (variable x) y el número de pie (variable y). La estadística demuestra que sigue una distribución bidimensional.
Los resultados de las medias no son muy elevados a causa de variedad de alturas y números de pie. También a causa del poco margen de los encuestados, ya que todos son de la misma edad, por tanto todos tienen más o menos la misma altura y el mismo número de pie.
El coeficiente de correlación linear demuestra que es positiva y fuerte a la vez, ya que se acerca a 1.
Los resultados obtenidos en las predicciones son resultados no muy elevados, ya que las repuestas de los encuestados oscilaban muy poco.
En conclusión, podríamos desglosar de todo los cálculos obtenidos, que la altura y el número de pie está bastante relacionado a causa del fuerte coeficiente de correlación linear. Pero como toda estadística los resultados no se ciñen 100% a la realidad, porque siempre existen excepciones si no tienen el coeficiente de correlación linear igual a .
![]()




Descargar
| Enviado por: | Alex |
| Idioma: | castellano |
| País: | España |