Estadística
Máximos y mínimos
MAXIMOS Y MINIMOS RELATIVOS
Con cierta frecuencia nos encontramos con la necesidad de buscar la mejor forma de hacer algo. En muchas ocasiones a través de los poderosos mecanismos de cálculo diferencial es posible encontrar respuesta a estos problemas, que de otro modo parecería imposible su solución.
Entre los valores q puede tener una función (Y) puede haber uno que sea el mas grande y otro que sea el mas pequeño. A estos valores se les llama respectivamente punto máximo y punto mínimo absolutos.
Si una función continua es ascendente en un intervalo y a partir de un punto cualquiera empieza a decrecer, a ese punto se le conoce como punto critico máximo relativo, aunque comúnmente se le llama solo máximo.
Por el contrario, si una funcion continua es decreciente en cierto intervalo hasta un punto en el cual empieza a ascender, a este punto lo llamamos puntro critico minimo relativo, o simplemente minimo.
Una funcion puede tener uno, ninguno o varios puntos criticos.
Curva sin máximos ni mínimos función sin máximos ni mínimos
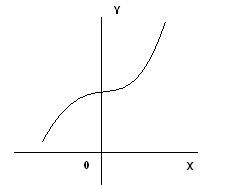
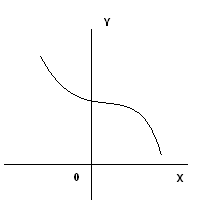
Función con un máximo curva con un máximo y un mínimo
Curva con un mínimo curva con varios mínimos y máximos
La pendiente de la recta tangente a una curva (derivada) en los puntos críticos máximos y mínimos relativos es cero, ya que se trata de una recta horizontal.
En los puntos críticos máximos, las funciones tienen un valor mayor que en su entorno, mientras que en los mínimos, el valor de la función es menor que en su entorno.
En un punto critico maximo relativo, al pasar la funcion de creciente a decreciente, su derivada pasa de positiva a negativa.
En un punto critico minimo relativo, la funcion deja de decrecer y empieza a ser creciente, por tanto, su derivada pasa de negativa a positiva.
METODOS PARA CALCULAR MAXIMOS Y MINIMOS DE UNA FUNCION
Para conocer las coordenadas de los puntos críticos máximos y mínimos relativos en una función, analizaremos dos mecanismos:
CRITERIO DE LA PRIMERA DERIVADA, UTILIZADO PARA UNA FUNCION CONTINUA Y SU PRIMERA DERIVADA TAMBIEN CONTINUA.
obtener la primera derivada.
igualar la primera derivada a cero y resolver la ecuación.
El valor o valores obtenidos para la variable, son donde pudiera haber máximos o mínimos en la función.
se asignan valores próximos (menores y mayores respectivamente) a la variable independiente y se sustituyen en la derivada. Se observan los resultados; cuando estos pasan de positivos a negativos, se trata de un punto máximo; si pasa de negativo a positivo el punto crítico es mínimo.
Cuando existen dos o más resultados para la variable independiente, debe tener la precaución de utilizar valores cercanos a cada uno y a la vez distante de los demás, a fin de evitar errores al interpretar los resultados.
sustituir en la función original (Y) el o los valores de la variable independiente (X) para los cuales hubo cambio de signo. Cada una de las parejas de datos así obtenidas, corresponde a las coordenadas de un punto crítico.
CRITERIO DE LA SEGUNDA DERIVADA
Este método es más utilizado que el anterior, aunque no siempre es más sencillo. Se basa en que en un máximo relativo, la concavidad de una curva es hacia abajo y en consecuencia, su derivada será negativa; mientras que en un punto mínimo relativo, la concavidad es hacia arriba y la segunda derivada es positiva.
Este procedimiento consiste en:
calcular la primera y segunda derivadas
igualar la primera derivada a cero y resolver la ecuación.
sustituir las raíces (el valor o valores de X) de la primera derivada en la segunda derivada.
Si el resultado es positivo, hay mínimo. Si la segunda derivada resulta negativa, hay un máximo.
Si el resultado fuera cero, no se puede afirmar si hay o no un máximo o mínimo.
sustituir los valores de las raíces de la primera derivada en la función original, para conocer las coordenadas de los puntos máximo y mínimo.
APLICACIÓN DE MAXIMOS Y MINIMOS RELATIVOS EN LA SOLUCION DE PROBLEMAS
Existen muchos campos del conocimiento (aritmética, geometría, economía, física, biología, industria, etc.) donde se presentan problemas que se resuelven aplicando los conceptos de máximos y mínimos del cálculo diferencial.
Para resolver los problemas a partir de los datos existentes, es importante en primer lugar, encontrar la expresión matemática de la función que represente el problema y cuyos valores máximos o mínimos se desean obtener.
Si la expresión matemática contiene varias variables, deberá plantearse en función de una sola; las condiciones del problema deben aportar suficientes relaciones entre las variables, para poderse expresar a todas ellas en función de una sola variable independiente.
Una vez que se tenga la función en la forma Y=f(X), se aplican las normas ya estudiadas.
En muchos problemas prácticos resulta muy sencillo identificar cuales valores críticos dan máximos o mínimos; y en consecuencia, ya no será necesario aplicar el procedimiento completo.
Es conveniente construir la grafica que represente la función en cuestión, a fin de verificar los resultados obtenidos.
PROBLEMAS
-
se tiene una lámina circular que tiene de radio 70 cm. De la que se desea cortar un rectángulo de la mayor área posible.
-
¿Qué medidas debe tener el rectángulo?
-
¿Cuál debe ser el área máxima)
Algunas formas de recortar rectángulos en el círculo
Si representamos la longitud del rectángulo con L. La anchura con A. siendo el diámetro D = 2 r = 140 cm. Puesto que el diámetro del círculo es la recta transversal del rectángulo, que lo divide en dos triángulos rectángulos:
Por el teorema de Pitágoras: L2 + A2 = D2 (140 cm.)2
L 2 + A2 = 19600
A = 19600 - L2
El área del rectángulo será Y = L A = L 19600 - L2 obteniendo el maximo de la función:
Y = L 19600 - L2
L2
Y = 19600 - L2 - 19600 - L2 se iguala la derivada a cero
L2
19600 - L2 - 19600 - L2 = 0 despejando L en la derivada
L = 9800 Al sustituir en la función:
Y = L 19600 - L 2 = 9800 19600 - 9800 = 9800
Para encontrar la anchura del cuadrado
A = 19600 - L = 19600 - 9800 = 9800
El rectángulo solución, resulto el cuadrado que mide por lado 9800 99 cm.
Correspondiéndole un área de 9800 cm2
-
con una malla de 380 m. se desea cercar un terreno rectangular.
-
¿Cuáles deben ser las medidas del terreno para que su área sea máxima?
-
Se pueden cercar infinidad de terrenos rectangulares con una malla de 380 m. aquí algunos casos.
| Terreno num. | largo | ancho | Perímetro | Área |
| 1 | 110 m. | 80 m | 380 m | 8800 m2 |
| 2 | 140 m. | 50 m | 380 m | 7000 m2 |
| 3 | 112 m. | 78 m | 380 m | 8736 m2 |
| 4 | 100 m. | 90 m | 380 m | 9000 m2 |
| 5 | 120 m. | 70 m | 380 m | 8400 m2 |
Suponiendo A = área del terreno, b = longitud y h = anchura, podemos plantear la función.
A = b h
Siendo una función de dos variables, ponemos una en función de la otra:
Perímetro de rectángulo = 2b +2h = 380
2b = 380 - 2h
b = 190 - h
la función con una variable es: A = (190 - h) h = 190 h - h2
Calculando el máximo de la función: A = 190 h - h2
A = 190 - 2 h
190 - 2 h = 0
h = 95
A = - 2 al ser negativa la segunda derivada, hay un máximo en h = 95
A = 190 h - h 2 = 190 (95) - (952) = 9025
B = 190 - h = 190 - 95 = 95
Por lo tanto, el terreno es un cuadrado que mide 95 m por lado y su área es de 9025 m2
-
a las 3:00 PM la persona A se encuentra a 150 Km. Al oriente de la persona B.
La persona A se dirige al poniente a razón de 10 Km./h y la persona B hacia el sur a 20 Km./h. Si ambos mantienen sus rumbos y velocidades
-
¿Cuándo estarán mas próximos entre si?
-
¿Cuál es la distancia mínima a la que se acercarían?
Consideremos A o y B o las posiciones de las personas a las 3:00 PM y A 1 y B1 sus posiciones X horas después.
La distancia recorrida en X horas es 10X y 20X respectivamente.
La distancia entre las dos personas (Y) se puede representar en la ecuación:
Y2 = (20X) 2 + (150 - 10X) 2 de donde:
Y = (20X) 2 + (150 -10X) 2 = 500X 2 - 3000X +22500
Calculando el mínimo de la función Y = 500X2 - 3000X + 22500
500X - 1500
Y =
500X2 - 3000X + 22500
500X - 1500
= 0 despejando X:
500X - 3000X + 22500
X = 3
Para X = 3 existe un mínimo en la función, por lo tanto después de tres horas se encuentran mas próximos entre si, es decir, a las 6:00 PM
La distancia que las separa en ese memento es:
Y= 500X2 - 3000X + 22500 = 500(3) 2 - 3000(3) + 22500 = 134. 164 Km.
-
De una lamina de 120 cm. X 75 cm. Se desea construir una caja sin tapa, del mayor volumen posible recortando cuadrados iguales de las esquinas de la lámina y doblando hacia arriba las salientes para tomar las caras laterales.
-
¿Cuáles deben de ser las dimensiones de la caja para que su volumen sea máximo?
-
¿Cuál es el volumen máximo que puede contener?
Las figuras muestran los cortes que se hacen a la lámina y la figura de la caja resultante.
Al asignar X a la altura de la caja y V a su volumen, se expresa algebraicamente:
V = (120 - 2X) (75 - 2X) (X)
V = 4X3 - 390 X2 + 9000X
No se le pude recortar a la lámina más de 37.5 cm., por lo que la altura debe estar en el intervalo: 0<X<37.5 Calculando el máximo en la función V = 4X3 - 390 X2 + 9000X
V = 12X2 - 780X + 9000
12X2 - 780X + 9000 = 0
X1 = 50 y X2 = 15 desde ahora puede descartarse el valor X = 50 por estar
Fuera del intervalo: 0< X<37.5
V” = 24X - 780 sustituyendo los valores X1 = 50 y X2 = 15 en la segunda
Derivada:
V” = 24 (50) - 780 = 420 por ser positivo, hay un mínimo para X = 50
V” = 24(15) - 780 = - 420 por lo tanto se encuentra el maximo que buscamos en
X = 15
Al sustituir an la funcion V = 4X3 - 390X2 + 9000X el valor X = 15, encontramos el volumen maximo de la caja:
V = 4(15) 3 - 390 (15)2 + 9000 (15)
V = 60 750 cm3
La altura debe ser X = 15cm
La longitud es (120 - 2X) = 120 - 2(15) = 90 cm.
La anchura es (75 - 2X) = 75 - 2(15) = 45 cm.
-
Encontrar dos números positivos cuya suma sea 144 y su producto sea máximo
Si representamos por P y Q los números buscados, tendremos la función Y = p Q como esta función depende de dos variables, ponemos una de ellas en función de la otra:
Como P +Q = 144, entonces P = 144 - Q y la función queda de una sola variable:
Y = Q (144 - Q) = 144 Q - Q2
Obtenemos el máximo de la función:
Y “= 144 - 2Q
144 - 2Q = 0
Q = 72
Y” = - 2 por ser negativa la segunda derivada, hay un maximo en Q = 72
Sustituyendo Q = 72 en la funcion Y = 144 Q - Q2
Y = 144 (72) - (72) 2 = 5184
P = 144 - Q = 144 - 72 = 72
Los numeros buscados son P = 72 y Q = 2 y su producto P Q = Y = 5184
-
Se lanza una pelota hacia arriba, desde una altura de 60 m. a una velocidad inicial de 34.3 m/seg. Considerando la gravedad = 9.81 m/seg2. calcular:
-
La altura máxima que alcanza la pelota respecto al piso.
-
El tiempo que tarda subiendo, bajando y durante todo el recorrido.
-
La velocidad al chocar con el piso.
-
La altura y velocidad por cada segundo que transcurre, hasta caer al piso.
La ecuación que representa el movimiento de la pelota es:
e = 60 +34.3 t - ½ g t2 = 60 + 34.3 t - 4.9 t2
Obtenemos el máximos de la función e = 60 + 34.3 t - 4.9 t2
e” = 34.3 - 9.8 t = V la velocidad es la derivada del espacio respecto al tiempo.
34.3 - 9.8 t = 0 En la parte mas alta, V = 0
t = 3.5
e” = - 9.8 la segunda derivada del espacio respecto al tiempo es la derivada de la velocidad
y es también la aceleración.
Al ser negativa la segunda derivada, hay un máximo en t = 3.5
Esto significa que la pelota tarda 3.5 segundos en llegar a la parte mas alta, que es:
e = 60 + 34.3 (3.5) - 4.9 (3.5)2 = 120.025
La altura máxima de la pelota con respecto al piso es de 120.025 m.
Para calcular el tiempo que tarda bajando, consideramos la ecuación a partir del punto mas alto
e = 120.025 = 4.9 t 2 de donde sustituimos t:
t = 120.025 = 4.95 seg.
4.9
Todo el trayecto se recorre en 3.5 seg. + 4.95 seg. = 8.45 seg.
La velocidad al caer al piso se puede obtener:
A partir del momento que se lanza:
e” = V = 34.3 - 9.8 t = 34.3 - 9.8 (8.45) = - 48.5 m/seg.
El signo negativo señala que la pelota va hacia abajo.
A partir del punto más alto:
e = 4.9 t2
e” = V = 9.8 t = 9.8 (4.95) = 48.5 m/seg.
Descargar
| Enviado por: | Edna Miriam Herrera Cardoso |
| Idioma: | castellano |
| País: | México |
