Matemáticas
Matrices y determinantes
INTRO. MATRICES Y DETERMINANTES
Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Tienen también muchas aplicaciones en el campo de la física.
MATRICES
Una matriz es una tabla ordenada de escalares ai j de la forma
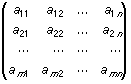
La matriz anterior se denota también por (ai j ), i =1, ..., m, j =1, ..., n, o simplemente por (ai j ).
Los términos horizontales son las filas de la matriz y los verticales son sus columnas. Una matriz con m filas y n columnas se denomina matriz m por n, o matriz m ð n.
Las matrices se denotarán usualmente por letras mayúsculas, A, B, ..., y los elementos de las mismas por minúsculas, a, b, ...
Ejemplo:
![]()
donde sus filas son (1, -3, 4) y (0, 5, -2) y sus
![]()
CLASES DE MATRICES
Según el aspecto de las matrices, éstas pueden clasificarse en:
Matrices cuadradas
Una matriz cuadrada es la que tiene el mismo número de filas que de columnas. Se dice que una matriz cuadrada n ð n es de orden n y se denomina matriz n-cuadrada.
Ejemplo: Sean las matrices
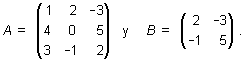
Entonces, A y B son matrices cuadradas de orden 3 y 2 respectivamente.
Matriz identidad
Sea A = (ai j ) una matriz n-cuadrada. La diagonal (o diagonal principal) de A consiste en los elementos a11, a22, ..., ann. La traza de A, escrito tr A, es la suma de los elementos diagonales.
La matriz n-cuadrada con unos en la diagonal principal y ceros en cualquier otra posición, denotada por I, se conoce como matriz identidad (o unidad). Para cualquier matriz A,
A· I = I ·A = A.
Matrices triangulares
Una matriz cuadrada A = (ai j ) es una matriz triangular superior o simplemente una matriz triangular, si todas las entradas bajo la diagonal principal son iguales a cero. Así pues, las matrices
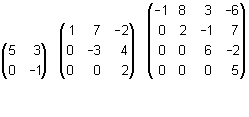
son matrices triangulares superiores de órdenes 2, 3 y 4.
Matrices diagonales
Una matriz cuadrada es diagonal, si todas sus entradas no diagonales son cero o nulas. Se denota por D = diag (d11, d22, ..., dnn ). Por ejemplo,
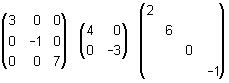
son matrices diagonales que pueden representarse, respectivamente, por
diag(3,-1,7) diag(4,-3) y diag(2,6,0,-1).
Traspuesta de una matriz
La traspuesta de una matriz A consiste en intercambiar las filas por las columnas y se denota por AT.
Así, la traspuesta de
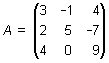
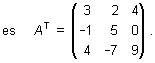
En otras palabras, si A = (ai j ) es una matriz m ð n, entonces AT = ![]()
es la matriz n ð m. La trasposición de una matriz cumple las siguientes propiedades:
1. (A + B)T = AT + BT.
2. (AT)T = A.
3. (kA)T = kAT (si k es un escalar).
4. (AB)T = BTAT.
Matrices simétricas
Se dice que una matriz real es simétrica, si AT = A; y que es antisimétrica,
si AT = -A.
Ejemplo:
Consideremos las siguientes matrices:
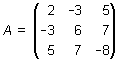

Podemos observar que los elementos simétricos de A son iguales, o que AT = A. Siendo así, A es simétrica.
Para B los elementos simétricos son opuestos entre sí, de este modo B es antisimétrica.
A simple vista, C no es cuadrada; en consecuencia, no es ni simétrica ni antisimétrica.
Matrices ortogonales
Se dice que una matriz real A es ortogonal, si AAT = AT A = I. Se observa que una matriz ortogonal A es necesariamente cuadrada e invertible, con inversa A-1 = AT.
Consideremos una matriz 3 ð 3 arbitraria:

Si A es ortogonal, entonces:

Matrices normales
Una matriz es normal si conmuta con su traspuesta, esto es, si AAT = ATA. Obviamente, si A es simétrica, antisimétrica u ortogonal, es necesariamente normal.
Ejemplo:
![]()
![]()
![]()
Puesto que AAT = ATA, la matriz es normal.
OPERACIONES CON MATRICES
Suma y resta de matrices
Para poder sumar o restar matrices, éstas deben tener el mismo número de filas y de columnas. Es decir, si una matriz es de orden 3 ð 2 y otra de 3 ð 3, no se pueden sumar ni restar. Esto es así ya que, tanto para la suma como para la resta, se suman o se restan los términos que ocupan el mismo lugar en las matrices.
Ejemplo:








Para sumar o restar más de dos matrices se procede igual. No necesariamente para poder sumar o restar matrices, éstas tienen que ser cuadradas.
Ejemplo:
![]()
![]()
![]()
![]()
![]()
Producto de matrices
Para poder multiplicar dos matrices, la primera debe tener el mismo número de columnas que filas la segunda. La matriz resultante del producto quedará con el mismo número de filas de la primera y con el mismo número de columnas de la segunda.
Es decir, si tenemos una matriz 2 ð 3 y la multiplicamos por otra de orden 3 ð 5, la matriz resultante será de orden 2 ð 5.
(2 ð 3) ð (3 ð 5) = (2 ð 5)
Se puede observar que el producto de matrices no cumple la propiedad conmutativa, ya que en el ejemplo anterior, si multiplicamos la segunda por la primera, no podríamos efectuar la operación.
3 ð 5 por 2 ð 3,
puesto que la primera matriz no tiene el mismo número de columnas que filas la segunda.
Supongamos que A = (ai j ) y B = (bi j ) son matrices tales que el número de columnas de A coincide con el número de filas de B; es decir, A es una matriz m ð p y B una matriz p ð n. Entonces el producto AB es la matriz m ð n cuya entrada ij se obtiene multiplicando la fila i de A por la columna j de B.
Esto es,

![]()
Ejemplo:
1.
![]()
2.
![]()
ð Producto por un escalar
El producto de un escalar k por la matriz A, escrito k·A o simplemente kA, es la matriz obtenida multiplicando cada entrada de A por k:

Ejemplo:
![]()
Entonces:
![]()
División de matrices
La división de matrices se define como el producto del numerador multiplicado por la matriz inversa del denominador. Es decir, sean las matrices A y B tal que A/B = AB-1:
Si una matriz está dividida entre un escalar, todos los términos de la matriz quedarán divididos por ese escalar.
Ejemplo:
![]()

MATRICES INVERTIBLES
Se dice que una matriz cuadrada A es invertible, si existe una matriz B con la propiedad de que
AB = BA = I
siendo I la matriz identidad. Denominamos a la matriz B la inversa de A y la denotamos por A-1.
Ejemplo:
![]()
![]()
![]()
Puesto que AB = BA = I, A y B son invertibles, siendo cada una la inversa de la otra.
Método de Gauss
Sea A = (ai j ) una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A-1, seguiremos los siguientes pasos:
Paso 1. Construir la matriz n ð 2n M = (A![]()
I ) esto es, A está en la mitad izquierda de M y la matriz identidad I en la derecha.
Paso 2. Se deja tal y como está la primera fila de M, y debajo del primer término de la diagonal principal, a11, que llamaremos pivote, ponemos ceros. Luego se opera como se indica en el siguiente ejemplo.
Ejemplo:
Consideremos una matriz 3 ð 3 arbitraria

Paso 1.

Paso 2.

El siguiente paso es igual que el anterior, pero esta vez se coge como pivote el segundo término de la diagonal principal.
Al llegar al último término de la diagonal, se procede igual que antes, pero poniendo los ceros encima del nuevo pivote. Se observa que al coger como pivote el último término de la diagonal, la matriz A se transforma en una matriz triangular.
Una vez realizados todos los pasos, la mitad izquierda de la matriz M se convierte en una matriz diagonal. En este momento hay que proceder a transformar, si es que no lo está, la mitad izquierda en la matriz identidad, dividiendo si fuera necesario las filas de M por un escalar.
Ejemplo:
Supongamos que queremos encontrar la inversa de

Primero construimos la matriz M = (A![]()
I),




La mitad izquierda de M está en forma triangular, por consiguiente, A es invertible. Si hubiera quedado toda una fila con ceros en la mitad A de M, la operación habría terminado (A no es invertible).
A continuación, cogemos como pivote a33, ponemos ceros encima de éste y seguimos operando hasta que nos quede una matriz diagonal.

Ya que la matriz colocada en la mitad izquierda es diagonal, no hay que operar más. Transformamos la matriz diagonal en una matriz identidad; para ello hay que dividir la segunda fila entre -1:

![]()
La matriz que ha quedado en la mitad derecha de M es precisamente la matriz inversa de A:

Para comprobar si el resultado es correcto, se procede a multiplicar AA-1, teniendo que dar como resultado la matriz identidad I.
Comprobación:
AA-1 = I

Ejercicio: operaciones con matrices
ððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððð
ð Sean

a) ¿Qué clase de matrices son?
b) Calcular:
- A - B + C.
A + B - C.
3A + C/2.
c) Calcular:
(A · B) /C.
d) Calcular la inversa de A (A-1) y comprobar el resultado.
Resolución:
a) Las tres matrices son cuadradas y de orden tres. A su vez, B es una matriz triangular, ya que todas las entradas debajo de la diagonal principal son ceros, y C es antisimétrica porque los elementos simétricos son opuestos entre sí.
b)


![]()



c)
ð Puesto que (A ð B) /C = A ð B ð C-1, calcularemos primero la inversa de C y luego haremos el producto.


ð Dividimos la primera fila entre -6, la segunda entre 3 y la tercera entre -3 para que en la mitad izquierda quede la matriz identidad,

ð Por lo tanto, la matriz inversa de C es:

ð A continuación, se calcula el producto de las matrices A y B,

ð Por último, calculamos (AðB)ðC-1.


= 
.
ð Sacando factor común 1/3, el resultado puede escribirse como:

d)
ð Primero se construye la matriz M = (A![]()
I) y luego se va desarrollando por Gauss. Así pues:


ð Se simplifica un poco para que las operaciones no sean tan costosas, dividiendo la tercera fila entre cuatro. De este modo, se tiene


.
Se vuelve a simplificar, dividiendo la primera fila entre dos y la segunda entre cuatro,

.
ð Puesto que ya ha quedado una matriz diagonal en la mitad izquierda de M, se procede a transformar esta mitad izquierda en una matriz identidad, dividiendo la primera fila entre -3042, la segunda entre -78 y la tercera entre 39,

Así pues, la matriz que ha quedado en la mitad derecha es precisamente la matriz identidad, que sacando factor común 1/78 se puede escribir como:

ð Para comprobar el resultado, la matriz inversa de A o A-1, tiene que cumplir
AA-1 = I.
Procedamos a la comprobación:



MATR. Y SIST. DE ECUAC. LINEALES
La matriz ampliada M de un sistema de m ecuaciones con n incógnitas es la siguiente:

Cada fila de M corresponde a una ecuación del sistema y cada columna a los coeficientes de una incógnita, excepto la última, que corresponde a las constantes del sistema.
Un sistema de ecuaciones lineales puede resolverse trabajando con su matriz ampliada, específicamente, reduciéndola a forma escalonada mediante el proceso de Gauss.
Método de Gauss
Para resolver sistemas de ecuaciones lineales, se aplica el método de Gauss. Este proceso se ilustra en el siguiente ejemplo.
Ejemplo:
Sea el sistema,

su matriz ampliada asociada es

Ahora resolvemos por el método de Gauss sabiendo que la primera columna corresponde a los coeficientes de la x, la segunda a los de la y, la tercera a los de la z y la cuarta a los términos independientes:






De este modo, el sistema tiene la solución única
x = 2, y = -1, z = 3.
La resolución de sistemas de ecuaciones lineales por matrices, aplicando el método de Gauss u otros, es una de las múltiples aplicaciones que tienen éstas.
Ejercicio: resolución de sistemas de ecuaciones lineales por matrices
ððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððð
ð Hallar el valor de x, y, z, t en los siguientes sistemas de ecuaciones lineales aplicando matrices:


a) La matriz M asociada al sistema de ecuaciones es:


La tercera fila se suprime, puesto que es múltiplo de la segunda y resultaría una fila nula. Así, el sistema queda formado por dos ecuaciones con cuatro incógnitas:

La solución del sistema es compatible e indeterminado, esto es, tiene infinitas soluciones.
x = -9 - y + 10t
z = 7t - 7 ó (- 9 - y + 10t, y, 7t - 7, t).
Dependiendo de qué valores se escojan para y y t, salen distintos resultados. Así, para y = t = 0 tendremos la solución del sistema
x = -9, y = 0, z = -7, t = 0.
b) La matriz M asociada al sistema de ecuaciones es:



No hay necesidad de continuar calculando nada más, puesto que la matriz escalonada ya nos indica que el sistema es incompatible (SI), es decir, que no tiene solución. Específicamente, la tercera fila de la matriz escalonada corresponde a la ecuación
0x + 0y + 0z + 0t = -5
obteniendo como resultado 0 = -5, que es absurdo. Por lo tanto, decimos que no tiene solución.
DETERMINANTES
A cada matriz n-cuadrada A = (ai j ) se le asigna un escalar particular denominado determinante de A, denotado por det (A), | A | o

Una tabla ordenada n ð n de escalares situada entre dos líneas verticales, llamada determinante de orden n, no es una matriz.
La función determinante apareció por primera vez en el estudio de los sistemas de ecuaciones lineales. Veremos que es una herramienta indispensable en el estudio y obtención de éstas.
DETERMINANTES DE ORDEN UNO Y DOS
Los determinantes de orden uno y dos se definen como sigue:
![]()
= a11
![]()
Así, el determinante de una matriz 1 ð 1 A = (a11) es el propio escalar a11, es decir, det (A) = |a11| = a11.
Ejemplos:
a) Dado que el determinante de orden uno es el mismo escalar, tenemos det (24) = 24, det(-3) = -3, det (3x+5) = 3x+5.
b)
![]()
![]()
DETERMINANTES DE ORDEN TRES
Consideremos una matriz 3 ð 3 arbitraria A = (ai j ). El determinante de A se define como sigue:

a12a21a33 - a32a23a11
Obsérvese que hay seis productos, cada uno formado por tres elementos de la matriz. Tres de los productos aparecen con signo positivo (conservan su signo) y tres con signo negativo (cambian su signo).
Para calcular los determinantes de orden tres, el siguiente diagrama puede ayudar a resolverlos:


Ejemplo:
Calcular el valor del determinante:

= 24 + 20 + 0 - (-4) - 0 - (-15) = 44 + 4 + 15 = 63
El determinante de la matriz 3 ð 3 A = (ai j ) puede reescribirse como:
det (A) = a11(a22a33 - a23a32) - a12(a21a33 - a23a31) + a13(a21a32 - a22a31) =
![]()
![]()
![]()
que es una combinación lineal de tres determinantes de orden dos, cuyos coeficientes (con signos alternantes) constituyen la primera fila de la matriz dada. Esta combinación lineal puede indicarse de la forma siguiente:



Nótese que cada matriz 2 ð 2 se obtiene suprimiendo en la matriz inicial la fila y la columna que contienen su coeficiente.
Ejemplo:
Para demostrar que la propiedad anterior se cumple, trabajaremos con :




![]()
![]()
![]()
= 3(8+5) - 2(0-10) + 1(0+4) = 39 + 20 + 4 = 63
PROPIEDADES DE LOS DETERMINANTES
Las propiedades básicas del determinante son las siguientes:
1. El determinante de una matriz A y el de su traspuesta AT son iguales, es decir,
![]()
2. Sea A una matriz cuadrada,
ð Si A posee dos filas (columnas) iguales, necesariamente ![]()
= 0.
ð Si A es triangular, esto es, A sólo tiene ceros por encima o por debajo de la diagonal principal, entonces ![]()
es igual al producto de los elementos de la diagonal.
3. Supongamos que B se ha obtenido de A mediante una operación elemental entre filas o columnas,
ð Si se han intercambiado dos filas (columnas) de A, |B| = - |A|.
ð Si se ha sumado un múltiplo de una fila (columna) a otra, entonces |B| = |A|.
ð Si se ha multiplicado una fila (columna) de A por un escalar k, |B| = k|A|.
4. Sea A cualquier matriz n-cuadrada, son equivalentes los siguientes principios:
ð A es invertible, es decir, A tiene inversa A-1.
ð AX = 0 tiene solamente la solución trivial.
ð El determinante de A no es nulo: |A| ð 0.
5. El determinante es una función multiplicativa. Es decir, el determinante del producto de matrices A y B es el producto de los determinantes: |AB| = |A| |B|.
6. Supongamos que A y B son matrices similares, entonces: |A| = |B|.
DETERM. DE ORDEN ARBITRARIO
Sea A = (ann) una matriz de orden arbitrario n ð n (siendo n un número par). Para calcular el det (A) se procede de la siguiente manera:

![]()
![]()

Los signos se van alternando según la posición que ocupen las entradas del determinante. Es decir:

Ejemplo:

Si observamos la matriz, podemos ver que en la tercera columna hay dos ceros. Así pues, si cogemos las entradas de la tercera columna para calcular el determinante, nos ahorraremos calcular dos determinantes, ya que el producto de un determinante por cero es cero.


+![]()
= -1(-35) + 3(35) = 35 + 105 = 140.
Ejercicio: cálculo de determinantes
ððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððð
ð Calcular los siguientes determinantes:
![]()
![]()





![]()
![]()




= 2(-6-24+16+2)+ 5(-4-24+6)-1(4+12-16-3) = -24-110+3 = -131.

![]()
= 1·(16+0+24-(-4)-(-30)-0) -2·(-128-2+30-(-40)-12-(-16)) = 74-2·(-56) =
= 74+112 = 186.
ADJUNTO DE UNA MATRIZ
Consideremos una matriz n-cuadrada A = (ai j ) sobre un cuerpo K. El adjunto de A, denotado por adj A, es la traspuesta de la matriz de cofactores de A:

Ejemplo:

Los cofactores de los nueve elementos de A son:
![]()
![]()
![]()
![]()
La traspuesta de la matriz de los cofactores anteriores proporciona el adjunto de A:

ð Aplicación del adjunto para hallar la matriz inversa
Para toda matriz cuadrada A,
A·(adj A) = (adj A) · A = |A|I
De este modo, si |A| ð 0,
![]()
Observemos que esta propiedad nos permite hallar por otro método la inversa de una matriz.
Ejemplo:
Consideremos la matriz

y el det A:

Así pues, aplicando la propiedad anterior:
![]()

Ejercicio: cálculo de la matriz inversa
ððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððð
ð Calcular, por la propiedad anterior, la inversa de las siguientes matrices:
a)
![]()
b)

a) Primero hallaremos el determinante de la matriz A:

El siguiente paso es hallar el adjunto de la matriz B, así pues, los cofactores de los cuatro elementos de B son:
B11 = 5 B12 = -2
B21 = 1 B22 = 3
y el adjunto de B, denotado por adj B, será
![]()
![]()
![]()
b) Empezaremos por hallar el det A,

Los cofactores de los nueve elementos de A son:
![]()
![]()
![]()
La traspuesta de la matriz de los cofactores anteriores proporciona el adjunto de A:

Aplicando la propiedad de la matriz inversa obtenemos A-1:


ððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððð
CÁLC. DEL RANGO DE UNA MATRIZ
Consideremos la matriz A = (aij):

1. El rango de la matriz A coincide con el de la matriz A' que se obtiene suprimiendo en la matriz A todas la líneas (filas o columnas) cuyas entradas estén sólo formadas por ceros, es decir, que sean nulas.
2. Consideremos la matriz:
A1 = (a11, a12, ..., a1n)
y supongamos que
![]()
entonces :
rango (A) ≥ rango(A 1) = 1
3. Añadimos filas de la matriz A a la matriz A1 hasta encontrar una matriz que cumpla:
![]()
tal que posea un menor no nulo de la forma:
![]()
Por consiguiente,
rango (A) ≥ rango(A 2) = 2.
Si esto no hubiese sido posible, entonces:
rango (A) = 1.
Supongamos que rango (A) ≥ rango (A2) y que i = 2 y j = 2.
4. Añadimos filas a la matriz A2 hasta encontrar una matriz que cumpla:

de forma que posea un menor de orden tres de la forma:

Entonces:
rango (A) ≥ rango (A2) = 3.
En caso de no haber sido posible encontrar dicho menor, entonces:
rango (A) = rango (A2) = 2.
Suponiendo que rango (A) ≥ rango (A3) y que i = 3 y j = 3, se procedería como en los casos anteriores, y así sucesivamente hasta agotar todas las filas de la matriz A.
Ejemplos:
a) Sea la matriz A una matriz de orden tres. Hallar el rango (A).

Como A es una matriz cuadrada de orden tres, como máximo el rango (A) puede valer tres. Calcularemos primero el determinante o determinantes de las submatrices de orden dos de A. Así pues
![]()
Ya que el resultado es cero, probaremos con todas las submatrices de A hasta encontrar una cuyo determinante no sea cero. Si no encontramos ninguna, el rango (A) = 1.
![]()
Puesto que el resultado de calcular el determinante de esta submatriz de A no es nulo, podemos afirmar de momento que el rango (A) = 2.
Añadimos ahora una columna y una fila más para ver si el rango puede ser tres:

Dado que el determinante de A no es nulo y a su vez es de orden tres, el rango
(A) = 3.
No necesariamente para poder calcular el rango de una matriz, ésta tiene que ser cuadrada. Así, en el siguiente ejemplo:
b) Calcular el rango de la matriz B de orden 3 ð 4.

![]()
![]()
Como hay una determinante de orden dos no nulo, el rango de la matriz B es mayor o igual que 2. Calculamos a continuación los determinantes de orden superior:

Probamos con un segundo determinante de orden tres:

Así pues, como hay un determinante de orden tres que no es nulo, el rango (B) = 3.
Un rango mayor que 3 no se puede hallar, ya que no se puede formar un determinante de orden 4. Recuérdese que para poder calcular el determinante de una matriz o de una submatriz, éstas tienen que ser cuadradas.
APLIC. DE LOS DETERMINANTES
En el tema de matrices y su aplicación a los sistemas de ecuaciones lineales, se vio cómo resolverlas mediante el teorema de Gauss. Con los determinantes, y aplicando la regla de Cramer, veremos otra manera de calcular los sistemas de ecuaciones lineales.
Regla de Cramer
Los pasos a seguir para calcular los sistemas de ecuaciones según la regla de Cramer son los siguientes:
1. Hallar la matriz ampliada (A![]()
b) asociada al sistema de ecuaciones, esto es: que la primera columna esté formada por las entradas de los coeficientes de la primera incógnita de las ecuaciones; que la segunda columna la formen las de la segunda incógnita, y así hasta llegar a la última columna, que estará constituida por las entradas de los términos independientes de las ecuaciones.
2. Calcular el determinante de A.
3. Aplicar la regla de Cramer, que consiste en:
a) ir sustituyendo la primera columna del det (A) por los términos independientes;
b) dividir el resultado de este determinante entre el det (A) para hallar el valor de la primera incógnita;
c) continuar sustituyendo los términos independientes en las distintas columnas para hallar el resto de las incógnitas.
Ejemplo:
Sea el sistema de ecuaciones lineales formado por dos ecuaciones con dos incógnitas:
![]()
Encontrar el valor de x e y mediante la regla de Cramer.
Empezaremos con el primer paso, que consiste en hallar la matriz ampliada A![]()
b asociada al sistema de ecuaciones lineales:

El segundo paso es calcular el determinante de A. Así pues:
![]()
Y el tercero y último paso consiste en calcular las incógnitas:

Discusión de los sistemas de ecuaciones lineales
A continuación, se estudiará la manera de saber de antemano si un sistema de ecuaciones lineales tienen o no solución y si tienen una única o infinitas soluciones.
El estudio o discusión de los sistemas de ecuaciones se efectúa aplicando el teorema de Rouché-Fröbenius. Éste dice que con un sistema de ecuaciones lineales pueden ocurrir dos cosas:
1. Que el sistema de ecuaciones sea un sistema compatible (S.C.), esto es, que tenga solución.
2. Que el sistema de ecuaciones sea un sistema incompatible (S.I.) o que no tenga solución.
El primer caso puede dividirse en dos:
a) que sea un sistema compatible y determinado (S.C.D.), esto es, que tenga una única solución;
b) que el sistema sea compatible e indeterminado (S.C.I.), es decir, que tenga infinitas soluciones.
Sea un sistema no homogéneo:

En consecuencia, la matriz ampliada Ab asociada al sistema de ecuaciones es:

y el sistema será compatible cuando:
rango (A) = rango (A![]()
b),
lo que suele expresarse diciendo que el rango de la matriz de coeficientes coincide con el rango de la matriz ampliada.
Si el sistema anterior es compatible y
rango (A) = rango (A![]()
b) = número de incógnitas,
el sistema es compatible y determinado, es decir, tiene una única solución.
Si, por el contrario, tenemos que
rango (A) = rango (A![]()
b) < número de incógnitas,
el sistema es compatible e indeterminado, es decir, tiene infinitas soluciones.
Si rango (A) ð rango (A![]()
b), el sistema es incompatible y no tiene ninguna solución.
Ejemplos:
Discutir, sin resolver, los siguientes sistemas de ecuaciones:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Puesto que rango (A) = 1 ð rango (A![]()
b) = 2, el sistema es incompatible; no existe ninguna solución.
![]()
![]()
![]()
![]()
![]()
Ya que rango (A) = rango (A![]()
b) = 2 = número de incógnitas, el sistema es compatible y determinado; es decir, existe una única solución.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Puesto que rango (A) = rango (A![]()
b) = 1 < número de incógnitas, el sistema es compatible e indeterminado; existen infinitas soluciones.
Ejercicio: cálculo de las incógnitas en un sistema de ecuaciones lineales
ððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððð
ð Discutir y calcular el valor de las incógnitas de los siguientes sistemas de ecuaciones lineales:

a)


Calculamos a continuación el rango de A y el rango de la matriz ampliada (A![]()
b):
El rango de la matriz A será:
![]()

El rango de la matriz ampliada (A![]()
b):

Dado que rango (A) = rango (A![]()
b) = 3 = número de incógnitas,
el sistema es compatible y determinado; tiene, pues, una única solución.
Resolvamos el sistema mediante la regla de Cramer:
Calculamos el det (A):

Aplicando la regla de Cramer:


![]()
![]()

![]()
![]()
x = 68/23; y = -53/23; z = -42/23.
ððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððð
POLINOMIO CARACTERÍSTICO
Consideremos una matriz n-cuadrada arbitraria:

La matriz (A - ð·In), donde In es la matriz identidad n-cuadrada y ð un escalar indeterminado, se denomina matriz característica de A:

Su determinante, det (A - ð·In) , que es un polinomio en ð, recibe el nombre de polinomio característico de A. Asimismo, llamamos a
det (A - ð·In) = 0
ecuación característica de A.
Ejemplo:
Hallar la matriz característica y el polinomio característico de la matriz A:
![]()
La matriz característica será (A - ð·In). Luego:
![]()
y el polinomio característico,
![]()
Así pues, el polinomio característico es ð 2 - ð + 4.
Valores propios y vectores propios
Sea A una matriz n-cuadrada sobre un cuerpo K.
Un escalar ð ð Kn se denomina un valor propio de A si existe un vector (columna) no nulo v ð Kn para el que
Av = ðv
Todo vector que satisfaga esta relación se llama vector propio de A perteneciente al valor propio ð. Los términos valor característico y vector característico (o autovalor y autovector) se utilizan con frecuencia en lugar de valor propio y vector propio.
Ejemplo:
Sea
![]()
![]()
![]()
y
![]()
![]()
![]()
Así pues, v1 y v2 son vectores propios de A pertenecientes, respectivamente, a los valores propios ð1 = 4 y ð2 = -1 de A.
Descargar
| Enviado por: | Jesus |
| Idioma: | castellano |
| País: | España |
