Matemáticas
Matemáticas
Ejercicios de matemáticas
Parcial 1º
Nota: No todo los ejercicios están resueltos; este escrito es todavía un borrador en su primera fase, por lo que no están introducidos los correspondientes comentarios. El hecho de fotocopiarlo y darlo a la luz es que puede servir de orientación al alumno interesado a pesar de que, como he dicho, es sólo un primer borrador en fase de elaboración.
Tema 1
Matrices y determinantes
Problema nº) Dada la matriz 
Calcule la matriz ![]()
, siendo ![]()
la matriz identidad de orden 3.
Encuentre para qué valores del parámetro ![]()
tiene inversa la matriz B.

Problema nº) Sea la matriz 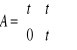
, ¿Para qué valores de t tiene inversa la matriz ![]()
?
Calcule la inversa de ![]()
cuando t=2

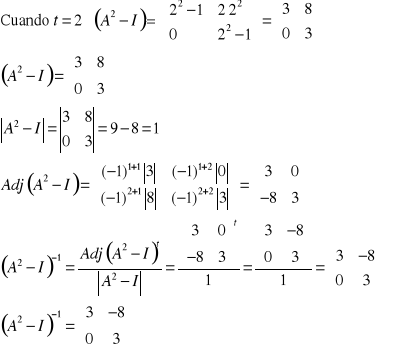
Problema nº) Calcule la matriz ![]()
, siendo 
, 
y 
.

Problema nº) Calcule la matriz ![]()
siendo:

, 
y 
.


Problema nº) Dadas las matrices 
y 
, calcule el valor de ![]()
.


Problema nº) Dadas las matrices 
y 
, calcule el valor de ![]()
.


Ecuaciones matriciales
Problema nº) Resuelva la siguiente ecuación matricial: ![]()
¿Qué condiciones han de cumplir las matrices A y B para que la ecuación tenga solución.

Problema nº) Resuelva la ecuación matricial ![]()
¿Qué condición deben cumplir las matrices A, B y C para que sea posible despejar la matriz X.

Problema nº) Resuelva la ecuación matricial ![]()
¿Qué condición deben cumplir las matrices A, B y C para que sea posible despejar la matriz X.

Problema nº) Resuelva la ecuación matricial siguiente:
![]()
¿Qué condición deben cumplir las matrices, A y B para que sea posible resolver la ecuación?

Problema nº) Resuelva la ecuación ![]()
, indicando qué condiciones han de verificar las matrices A, B y C para que esto sea posible.

Problema nº) Resuelva la ecuación matricial ![]()

Problema nº) Resuelva la ecuación matricial siguiente:
![]()
¿Qué condición deben cumplir las matrices A y B para que sea posible resolver la ecuación?

Problema nº) Resuelva la siguiente ecuación matricial ![]()
¿Qué condición debe cumplirse para que sea posible resolver la ecuación?

Problema nº) Dadas las matrices: 

y 
a) Resuelva la siguiente ecuación matricial ![]()
b) Sustituya en el resultado obtenido en el apartado anterior los valore de las matrices del enunciado y obtenga la matriz X.

La matriz ![]()
tiene que ser regular, es decir que su determinante tiene que ser distinto de cero, así tiene inversa y entonces el sistema tiene solución.

Problema nº) Resuelva la ecuación matricial siguiente:![]()
¿Qué condición debe cumplirse para que sea posible resolver la ecuación?

Problema nº) Resuelva la ecuación matricial ![]()
, indicando qué condiciones han de verificar las matrices A y B para que esto sea posible.

Problema nº) Resuelva la ecuación matricial indicando que debe cumplirse para que sea posible resolverla:
![]()

Problema nº) Sean las matrices 
y 
.
Calcule la matriz ![]()
Resuelva la ecuación matricial ![]()
, y obtenga la matriz X, sabiendo que ![]()



Problema nº) Dadas las matrices 
, 
, resuelva la ecuación matricial ![]()


Matrices estocásticas
Problema nº) Dos empresas A y B comparten el mercado de un cierto bien. Las ventas de cada empresa son las siguientes: la empresa A vende 150 unidades y la empresa B vende 350 unidades. Sabiendo que a lo largo del año ocurren los siguientes cambios:
A conserva el 65% de sus clientes, cediendo a B el 35%,
B conserva el 40% de sus clientes, cediendo a A el 60%.
Calcule la cuota de mercado pasados 2 años. ¿Qué expresión determina la cuota de cada empresa pasados “n” años?

Problema nº) Dos empresas A y B comparten el mercado de un cierto bien. Las ventas de cada empresa son las siguientes: la empresa A vende 200 unidades y la empresa B vende 150 unidades. Sabiendo que a lo largo del año ocurren los siguientes cambios:
A conserva el 75% de sus clientes, cediendo a B el 25%,
B conserva el 60% de sus clientes, cediendo a A el 40%.
Determine la correspondiente matriz de transición de ventas.
¿Cuál es la cuota de mercado de cada empresa pasados dos años?
¿Qué expresión determina la cuota de cada empresa pasados n-años?

Problema nº) Tres empresas A, B y C comparten el mercado de un cierto bien. Las ventas de cada empresa son las siguientes: la empresa A vende 40000 unidades, la empresa B vende 20000 y la empresa C vende 30000. Sabiendo que a lo largo del año ocurren los siguientes cambios:
A conserva el 90% de sus clientes, cediendo a B el 5% y a C el 5%.
B conserva el 80% de sus clientes, cediendo a A el 10% y a C el 10%.
C conserva el 85 de sus clientes, cediendo a A el 5% y a B el 10%.
Determine la correspondiente matriz de transición de ventas.
¿Cuál es la cuota de mercado de cada empresa pasado un año?
¿Cómo calcularía la cuota de mercado pasados 6 años, suponiendo que la matriz de transición no varía? Demuestre la fórmula que utilizaría.

Problema nº) La siguiente matriz de probabilidad:

indica las probabilidades de que los clientes de tres almacenes C, P y E que un mes compraron en alguno de ellos, al mes siguiente sigan fieles al mismo o se vayan a uno de los otros dos. Si un mes los clientes de C, P y E fueron respectivamente 40000, 80000 y 60000, calcule:
¿Cuál será el número previsto de clientes que vaya a cada uno de los almacenes el próximo mes?
Indique de forma matricial cómo hallaría el número de clientes previstos de cada gran almacén pasados 3 meses?

Problema nº) Tres empresas A, B y C comparten el mercado de un cierto bien. Las ventas de cada empresa son las siguientes: la empresa A vende 2000 unidades, la empresa B vende 1500 y la empresa C vende 3000. Sabiendo que a lo largo del año ocurren los siguientes cambios:
A conserva el 85% de sus clientes, cediendo a B el 10% y a C el 5%.
B conserva el 65% de sus clientes, cediendo a A el 15% y a C el 20%.
C conserva el 75 de sus clientes, cediendo a A el 20% y a B el 5%.
Determine la correspondiente matriz de transición de ventas.
¿Cuál es la cuota de mercado de cada empresa pasado un año?
¿Cómo calcularía la cuota de mercado pasados 6 años, suponiendo que la matriz de transición no varía? Demuestre la fórmula que utilizaría.

Problema nº) Tres empresas A, B y C comparten el mercado de un cierto bien. Las ventas de cada empresa son las siguientes: la empresa A vende 200 unidades, la empresa B vende 150 y la empresa C vende 300. Sabiendo que a lo largo del año ocurren los siguientes cambios:
A conserva el 75% de sus clientes, cediendo a B el 15% y a C el 10%.
B conserva el 60% de sus clientes, cediendo a A el 5% y a C el 35%.
C conserva el 85 de sus clientes, cediendo a A el 10% y a B el 5%.
Determine la correspondiente matriz de transición de ventas.
¿Cuál es la cuota de mercado de cada empresa pasado un año?
¿Cómo calcularía la cuota de mercado pasados 4 años, suponiendo que la matriz de transición de ventas se mantiene constante? Indique el cálculo que realizaría.
Problema nº) Desde hace años los científicos estudian los hábitos migratorios de algunas especies de animales salvaje. Un censo anual se lleva a cabo en tres regiones habitadas por las especies. Se ha observado un patrón estable de cambios en sus movimientos. El patrón se advierte en la siguiente matriz de transición
Suponga que las poblaciones de las tres regiones fueron 40000, 20000 y 30000 durante el último censo. Prediga las poblaciones de cada región al momento de hacerse el próximo censo (dentro de un año) ¿Y cuál será al cabo de 2 años?
Redes
Problema nº) (Problema todavía sin resolver e incompleto) Dada la siguiente matriz adyacente 
Dibuje la correspondiente red. Calcule ![]()
y explique que representa el elemento que ocupa la 2ª fila y la 3ª columna de dicha matriz.

HHHHHHHHHHH
HHHHHHHHHHHH
junio 2001 2º parcial
Problema nº) (Problema todavía sin resolver e incompleto) Los nudos A, B, C y D representan cuatro aeropuertos los arcos los trayectos que recorren los aviones de una compañía aérea. I tenemos la siguiente red
Mmmmmmmmmmmmmmmmmmm
mmmmm
Escriba la matriz adyacente A
Después de calcular la matriz ![]()
, ¿qué representa el elemento que ocupa la 2ª fila y 3ª columna de dicha matriz?
¿Qué cálculo realizaría para saber las rutas entre dos aeropuertos con tres escalas?
HHHHHHHHHH
HHHHHHHHHHHHHHH
final 2º llamamiento 12 julio 2002 1º y 2º parcial
Problema nº) (Problema todavía sin resolver e incompleto) La siguiente figura es un diagrama de redes que muestra la estructura de rutas entre pueblos de una provincia de una pequeña empresa de autobuses, la cual da servicio a cuatro pueblos representados por las letras A, B, C y D. A partir de la siguiente figura:
Mmmmmmmmmmmmm
Construya la correspondiente matriz adyacente.
Determine aplicando el cálculo matricial el número de servicios que hay entre A y B haciendo una ruta intermedia.
HHHHHHHHH
HHHHHHHHHHHHH
2º llamamiento 2 de julio de 2004
Problema nº) (Problema todavía sin resolver e incompleto) Las direcciones para circular en coche por 5 plazas de una ciudad se indican en el siguiente diagrama.
mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm
Construya la correspondiente matriz adyacente M.
Indique lo que representa en la matriz adyacente los elementos ![]()
y ![]()
Calcule la matriz que indica el número de caminos distintos que hay entre dos plazas haciendo una escala intermedia.

![]()
significa que no hay ninguna ruta de C a B con cero escalas intermedias.
![]()
significa que hay una ruta de A a B con cero escalas intermedias.

Tema 2
Sistemas de ecuaciones
Problema nº) Dada la matriz 
Calcule ![]()
, donde I es la matriz identidad de orden 3.
Determine los valores de ![]()
para que ![]()
¿Para qué valores de ![]()
existe la inversa de la matriz ![]()
Para cada valor de ![]()
resuelva el sistema ![]()
donde 


Problema nº) Dada la matriz 
, halle los valores del parámetro ![]()
para los que ![]()
Resuelva el sistema de ecuaciones ![]()
para ![]()
, donde ![]()
y la matriz 

Problema nº) Discuta y resuelva el sistema según los valores del parámetro ![]()
:

Problema nº) Establezca razonadamente la compatibilidad o incompatibilidad del sistema de ecuaciones:

En caso de compatibilidad, encuentre el valor de la variable x.

Problema nº) Una empresa produce tres productos A, B y C, que procesa en tres máquinas. El tiempo requerido para procesar una unidad de cada producto por las tres máquinas está dado por:
![]()

Se disponen de la máquina I por 850 horas, de la máquina II por 1200 horas y de la máquina III por 550.
¿Cuántas unidades de cada producto deberían producirse con objeto de emplear todo el tiempo disponible las máquinas?

Problema nº) Un proceso de mezclado debe combinar res componentes de modo que se cree una mezcla final de 60000 litros. Los tres componentes cuestan 2 euros, 1.50 euros y 1.25 euros por litro respectivamente. El precio total de los componentes deberá ser de 90000 euros. Otra restricción de la mezcla consiste en que la cantidad de litros utilizados del componente 1 deberá ser la misma que se unas del componente 2. Determine si hay una combinación de los tres componentes que lleve a una mezcla final de 60000 litros con un costo de 90000 euros y que además se ajusten a las restricciones.

Problema nº) Una compañía elabora tres productos que han de procesarse en un departamento. En la tabla adjunta se resumen las necesidades de horas de trabajo y materias primas por unidad de cada producto. Cada mes cuenta con 1300 horas de trabajo y 4700 kilos de materias primas, si la producción mensual combinada de los tres productos ha de ser de 400 unidades, averigüe si hay combinaciones de los tres productos que aprovechen al máximo las disponibilidades mensuales de trabajo y de materias primas, alcanzando además la meta de 400 unidades.
| Producto | |||
| 1 | 2 | 3 | |
| Horas de trabajo/unidad | 5 | 2 | 4 |
| Kilos de materias primas/unidad | 15 | 10 | 12 |
Escriba el sistema de ecuaciones lineales correspondientes que relaciona las diferentes variables del problema.
Halle el número de unidades que se han de fabricar del primer producto.

Problema nº) Aplique el método de Gauss para resolver el sistema:


Matrices Input-Output
Problema nº) Sea la matriz tecnológica de un sistema económico con 3 industrias:

y sean ![]()
, ![]()
, ![]()
las cantidades producidas por cada industria y supongamos que las demandas no industriales son:
![]()
![]()
![]()
Escriba el sistema de ecuaciones que expresa la situación de equilibrio (la demanda total y la oferta coinciden)
Escriba el sistema de ecuaciones anterior en forma matricial y despeje la matriz de incógnitas ¿Qué condición deben cumplir las matrices para que sea posible despejar la matriz de incógnitas?

Problema nº) En una economía hay tres sectores productivos, A, B y C. La matriz input-output del sistema está dada por:

¿Genera la matriz input-output una economía productiva?

Problema nº) En una economía hay tres sectores productivos A, B y C. En la siguiente matriz input-output del sistema se da la cantidad de producto de cada sector necesaria para producir una unidad de producto de los otros sectores y de él mismo. Sabiendo que la demanda externa del sistema es de 1200 de producto del sector A, 3400 del sector B y 140 del sector C.
| Sector A | Sector B | Sector C | |
| Sector A | 0.6 | 0 | 0.3 |
| Sector B | 0.4 | 0.2 | 0.6 |
| Sector C | 0 | 0.3 | 0.6 |
Plantee sin resolver el sistema que expresa la situación de equilibrio.
¿Genera la matriz input-output una economía productiva? Razone la respuesta.

Problema nº) La matriz tecnológica de tres industrias es 
y las demandas no industriales en millones de euros son, respectivamente 200, 120 y 300.
Determine los niveles de equilibrio de producción en las tres industrias.
Estudie si la matriz tecnológica determina una economía productiva.

Problema nº) La matriz tecnológica para un modelo de tres industrias es: 
La demanda no industrial de la producción de las industrias mencionadas es ![]()
millones de euros, ![]()
millones de euros y ![]()
millones de euros.
Determine el sistema de ecuaciones que expresa la situación de equilibrio del modelo. Escriba el sistema en forma matricial y despeje la matriz de incógnitas en la ecuación matricial.
Indique el significado de los elementos ![]()
y ![]()
.
¿Qué condición debe cumplir para que la matriz A genere una economía productiva.
Problema nº) La matriz tecnológica para un modelo input-output de tres industrias es:

La demanda no industrial de la producción de las industrias mencionadas es de ![]()
millones de euros, ![]()
millones de euros y ![]()
millones de euros.
Determine el sistema de ecuaciones que expresa la situación de equilibrio del modelo.
Escriba el sistema en forma matricial y despeje la matriz de incógnitas que proporciona los niveles de producción en equilibrio. 
Problema nº) Consideremos la matriz tecnológica de un sistema económico formado por 3 sectores:

Sean ![]()
, ![]()
, ![]()
las cantidades producidas por cada sector y supongamos que las demandas externas están dadas por:
![]()
![]()
![]()
Indique el significado de los coeficientes ![]()
, ![]()
, ![]()
de la matriz input-output del sistema.
Determine los niveles de producción ![]()
, ![]()
, ![]()
necesarios para que la oferta y la demanda total estén en equilibrio.

Problema nº) Considere una economía con dos industrias: energía eléctrica y servicios. La producción de 1 u.m. de energía eléctrica requiere 0.01 u.m. de dicha energía y 0.05 u.m. de servicios. Para dar lugar a 1 u.m. de servicios se necesario 0.30 u.m. de energía eléctrica y 0.10 u.m. de servicios. Cada semana la demanda externa de energía eléctrica es de 100000 u.m. mientras que la de servicios es de 400000 u.m.
a) Determine el nivel de producción total de dichos factores productivos.
b) Estudie si dicha economía es productiva.

Problema nº) Una fábrica produce dos bienes A y B. Para fabricar una u.m. del bien A se requieren 0.3 unidades de A y 0.2 unidades de B y para fabrica una u.m. de B se requieren 0.15 unidades de A y ![]()
unidades de B. Sabiendo que existe una demanda externa por valor de 500 u.m. del bien A y 1000 u.m. del bien B, determine:
a) El sistema de ecuaciones que define la situación de equilibrio del sistema.
b) Escriba es sistema de ecuaciones en forma matricial, despeje la matriz de producción que determina los valores de equilibrio del sistema.
c) Halle el valor de ![]()
para que la matriz input-output genere una economía productiva.

Problema nº) Dada la matriz input-output para dos sectores de producción 
donde ![]()
.
Determine los valores del parámetro ![]()
para que la matriz A genere una economía productiva.

Problema nº) Determine para qué valores del parámetro ![]()
, la matriz input-output 
genera una economía productiva

Problema nº) Una fábrica produce dos bienes A y B. Para fabricar una u.m. del bien A se requieren 0.3 unidades de A y 0.2 unidades de B y para fabrica una u.m. de B se requieren 0.15 unidades de A y 0.05 unidades de B. Sabiendo que existe una demanda externa por valor de 500 u.m. del bien A y 1000 u.m. del bien B, determine:
a) El sistema de ecuaciones que define la situación de equilibrio del sistema.
b) Genera la matriz input-output una economía productiva.

Si genera una economía productiva.
Problema nº) Una fábrica produce dos bienes A y B. Para fabricar 1 u.m. del bien A se requieren 0.1 unidades de B y para fabrica 1 u.m. de B se requieren 0.15 unidades de A y 0.05 unidades de B. Sabiendo que existe una demanda externa por valor de 500 u.m. del bien A y 1000 u.m. del bien B, determine:
a) El sistema de ecuaciones que define la situación de equilibrio del sistema. Exprese el sistema en forma matricial y despeje la matriz de incógnitas de la ecuación matricial.
b) Genera la matriz input-output una economía productiva.

Tema 3
Espacios vectoriales
Problema nº) Sea el subespacio vectorial de ![]()
dado por:
![]()
Se pregunta:
1) Determine una base de S.
2) Halle las componentes del vector ![]()
en la base hallada.

Problema nº) Sean los vectores ![]()
Estudie razonadamente la dependencia e independencia lineal de los vectores según los valores de ![]()
.
Halle para qué valores de ![]()
los vectores ![]()
son ortogonales.


Problema nº) Dado el siguiente subconjunto de ![]()
: ![]()
![]()
Demuestre que es un subespacio vectorial.
Halle una base y determine su dimensión.

Problema nº) Sea el subespacio vectorial S definido por:
![]()
Encuentre una base y determine la dimensión del subespacio vectorial.
Halle las ecuaciones paramétricas del subespacio.
Determine el vector que en la base hallada tiene de coordenadas (-2,3)

Problema nº) Sea el subespacio vectorial:
![]()
Encuentre una base de S y determine la dimensión del subespacio.
Determine las coordenadas del vector (0,-1,1,1) en la base hallada

Problema nº) Sea el subespacio vectorial S definido por:
![]()
Encuentre una base de S y determine la dimensión del subespacio.
Determine las ecuaciones paramétricas del subespacio S.
Determine el vector que en la base hallada tiene de coordenadas del vector (-2,3).

Problema nº) Encuentre una base, la dimensión y las ecuaciones paramétricas del subespacio vectorial dado por ![]()

Problema nº) Encuentre una base, la dimensión y las ecuaciones paramétricas del subespacio vectorial dado por ![]()
![]()

Problema nº) Dado el siguiente subespacio vectorial:
![]()
Halle la dimensión y una base.
Halle las ecuaciones paramétricas.
Dado el vector ![]()
halle sus coordenadas en la base hallada.
Halle el vector cuyas coordenadas en la base hallada son (2,3).

Problema nº) Sea el subespacio vectorial ![]()
Encuentre una base y la dimensión de S. halle las ecuaciones paramétricas del subespacio.
Calcule el vector que en la base hallada tenga por coordenadas (1,-2).
¿Qué valor ha de tomar a para que ![]()
?

Problema nº) Dado el siguiente subespacio vectorial:
![]()
a) Halle la dimensión y una base.
b) Determine las ecuaciones paramétricas del subespacio.
c) Calcule las coordenadas del vector (5,7,2,10) en la base hallada.

Problema nº) Sea el subespacio vectorial S definido
![]()
Encuentre una base de S y determine la dimensión del subespacio vectorial.
Determine el vector que en la base hallada tiene de coordenadas (2,3).
Si un vector en la base canónica tiene de componentes (6,6,4,2), determine dichas componentes en la base hallada.

Problema nº) Sea ![]()
Encuentre una base de S y diga su dimensión.
Determine el vector del subespacio que en la base hallada tiene de coordenadas (2,2)
Calcule las coordenadas del vector (3,1,4,2) en la base hallada.
Halle las ecuaciones paramétricas del subespacio.

Problema nº) Sea el subespacio vectorial definido por:
![]()
Encuentre una base de S y determine la dimensión del subespacio.
¿Pertenece el vector ![]()
a S? ¿Y el vector ![]()
? En caso afirmativo calcule sus coordenadas en la base hallada

Problema nº) Sea ![]()
un subconjunto de ![]()
, ¿es S un subespacio vectorial? Razone la respuesta.
En caso afirmativo:
Calcule la dimensión y una base.
Calcule las coordenadas del vector (0,1,-1,0) en la base hallada.
Determine el vector que en la base hallada tiene como coordenadas (1,0,1)
Halle las ecuaciones paramétricas.

Tema 4
Funciones
Problema nº) Un museo cobra la entrada cobra la entrada de los grupos de visitantes de acuerdo con la siguiente política: a grupos de menos de 50 personas a 2.50 € por persona; a grupos de 50 o más personas a 1.80 € por persona.
Exprese la cantidad que se cobrará por la admisión de un grupo como función una función del tamaño, y dibuje su gráfica.
¿Cuánto dinero se ahorrará un grupo de 49 personas en los costos de las entradas en total si consiguen reclutar a un visitante más?

Problema nº) Un fabricante de muebles puede vender mesas a 70 euros cada una. El coste total para el fabricante está constituido por los costes indirectos fijos de 8000 euros más costes de producción de 30 euros por mesa.
¿Cuántas mesas debe vender el fabricante para alcanzar el punto de equilibrio?
¿Cuántas mesas debe vender el fabricante para obtener un beneficio de 6000 euros?
¿Cuál será el beneficio o la pérdida del fabricante si vende 150 mesas?
En un mismo conjunto de ejes elabore la gráfica de las funciones de ingreso total y coste total para el fabricante

Problema nº) La funciones de oferta y demanda para cierto artículo son ![]()
y ![]()
, respectivamente.
Encuentre el precio de equilibrio y la cantidad correspondiente de unidades ofrecidas y demandadas.
Dibuje las curvas de oferta y demanda en el mismo conjunto de ejes.
¿Dónde corta la curva de demanda al eje p?

Problema nº) Un cuadro tiene un valor de 2000 euros en la actualidad. Sabiendo que el valor del cuadro aumenta un 3% cada año en relación con el valor anterior, encuentre la función que exprese el valor del cuadro dentro de t años. Represente la gráfica de la función obtenida.

Problema nº) El valor de un inmueble crecerá un 3% cada año. El valor actual es de 1000000 de euros.
Exprese mediante una función el valor del inmueble dentro de t años y represente su gráfica.
Determine el tiempo que ha de transcurrir para que el valor del inmueble aumente un 75%.
Determine la tasa de cambio del valor del inmueble pasados 4 años.

Problema nº) Un fabricante compra maquinaria por valor de 20000 euros. Ésta se deprecia linealmente de manera que después de 10 años su valor comercial será de 1000 euros.
Exprese el valor de la maquinaria como función de su antigüedad y dibuje la gráfica.
Calcule el valor de la maquinaria después de 4 años.

Problema nº) El valor de una cosechadora de trigo se deprecia un 5% cada año respecto del precio del año anterior. Dado que la máquina costó 140000 euros, se pide:
a) El valor de la máquina en función del tiempo t expresado en años.
b) El valor de la máquina al cabo de 12 años.
c) Represente gráficamente la función hallada.

Problema nº) Una empresa compra maquinaria por valor de 20000 euros. Exprese el valor de las máquinas en función de su antigüedad y represente la gráfica de la función en los casos siguientes:
a) El valor de las máquinas se desprecia linealmente, de manera que después de 10 años su valor comercial será de 2000 euros.
b) El valor de la máquina disminuye 5% cada año.


Problema nº) Una empresa compra una envasadora de paquetes harina por calor de 40000 euros. Exprese el valor de la máquina en función de la antigüedad y represente la gráfica de la función en los casos siguientes:
El valor de la máquina se deprecia linealmente, de manera que después de 10 años su valor comercial será de 15000 euros.
El valor de la máquina disminuye un 8% cada año.


Problema nº) Una empresa compra maquinaria por valor de 20000 euros. Exprese el valor de las máquinas en función de su antigüedad y represente la gráfica en los casos siguientes:
El valor de las máquinas se deprecia linealmente, de manera que después de 10 años su valor comercial será de 2000 euros.
El valor de la máquina crece un 3% cada año.


Problema nº) El valor de una máquina sube de precio un 2.5% cada año, pero a interés compuesto.
¿Cuál será el valor de la máquina dentro de 8 años si inicialmente valía 45000 euros?
¿Cuál será el valor dentro de t años?

Problema nº) El valor de un inmueble crece un 4% cada año. Sabiendo que el valor inicial del mismo es de 300000 euros.
Determine el valor del inmueble pasados 15 años.
¿Cuánto tiempo debe transcurrir para que se duplique el valor del inmueble?


Problema nº) El valor de un piso de segunda mano incrementa su valor un 5% cada alo sobre el valor del año anterior. Sabiendo que inicialmente costó 120000 euros, hallar.
El valor del piso pasados 10 años.
El número de años que deben transcurrir para que el piso duplique su valor.


Continuidad
Problema nº) ¿Qué valores debe tomar a y b para que la función 
sea continua en el dominio de definición?
![]()


Cálculo de Derivadas
Problema nº) Calcule la derivada de la siguiente función: ![]()

Problema nº) Calcule la derivada de la siguiente función: ![]()
![]()
Problema nº) Calcule la derivada de la siguiente función:
![]()

Problema nº) Calcule la derivada de la siguiente función:
![]()
![]()
Problema nº) Calcule la derivada de la siguiente función:
![]()

Diferencial
Problema nº) El coste total para un fabricante cuando se producen x unidades está dado por ![]()
. Si el nivel de producción actual es de 40 unidades, determine aproximadamente aplicando la diferencial el incremento porcentual del coste si se pasa a producir 40.5 unidades.

Problema nº) La producción diaria de cierta fábrica está dada por la función ![]()
unidades, donde K representa la inversión de capital. Si la inversión actual es de 400 unidades, estime aplicando la diferencial el cambio porcentual en la producción si el capital invertido se incrementa en 0.85 unidades.

Problema nº) En cierta fábrica, la producción diaria ![]()
unidades, donde K representa la inversión de capital medida en unidades de 1000 euros. Si la inversión actual de capital es de 900000 euros, calcule el efecto que tendrá sobre la producción diaria una inversión de capital adicional de 800 euros.

Problema nº) En una fábrica la producción mensual está dada por ![]()
, donde K representa la inversión en capital. Sabiendo que el nivel actual de inversión de capital es de K=25, determine aproximadamente aplicando le diferencial el cambio porcentual que se produce cuando hay un incremento de 0.5 unidades en la inversión de capital.

Problema nº) En una fábrica la producción mensual está dada por ![]()
, donde K representa la inversión en capital. Sabiendo que el nivel actual de inversión de capital es de K=25, determine aproximadamente aplicando le diferencial el cambio porcentual que se produce cuando hay un incremento de 0.5 unidades en la inversión de capital.

Problema nº) En una fábrica la producción mensual está dada por ![]()
, donde K representa la inversión de capital. Sabiendo que el nivel actual de inversión de capital es K=14, determine aproximadamente aplicando la diferencial el incremento porcentual que se produce cuando hay un incremento de 0,5 unidades en la inversión de capital.

Problema nº) En cierta fábrica, la producción diaria es ![]()
unidades, donde K representa la inversión de capital de la empresa.
Aplique la diferencial para calcular el incremento en la producción si el capital se incrementa en 0.5 unidades. Supongamos que la inversión de capital es de 64 unidades.
Aplique la diferencial para calcular el incremento porcentual que se requiere en la inversión de capital para lograr un aumento de 1.2% en la producción.

Problema nº) Las ganancias anuales brutas de cierta compañía fueron ![]()
miles de euros t años a partir de la finalización de 1993. Aplique la diferencial para calcular aproximadamente el cambio porcentual de las ganancias anuales brutas durante el tercer trimestre.

Problema nº) El producto nacional bruto (PNB) de un cierto país era ![]()
miles de millones de euros t años después del 1 de enero de 2000.
¿A qué tasa cambiará el PNB con respecto al tiempo al final del año 2005?
¿A qué tasa porcentual cambiará el PNB con respecto al tiempo al final del año 2005?
Aplique la diferencial para determinar aproximadamente el incremento del PNB cuando t pasa de 3 a 3.5.

Problema nº) El ingreso total mensual de un fabricante es ![]()
euros cuando se producen q unidades durante el mes. En la actualidad el fabricante produce 80 unidades al mes y planea disminuir la producción mensual en 0.65 unidades. Calcule el cambio del ingreso total mensual como resultado de esta disminución.

Problema nº) Los beneficios B de una empresa vienen dados por ![]()
Aproxime el cambio de los beneficios cuando la producción cambia de ![]()
a ![]()
unidades, y el cambio porcentual del beneficio en esa misma circunstancia.

Tasa de cambio
Problema nº) El valor de un inmueble con respecto al tiempo t medido en años viene dado por la función ![]()
. Determine la tasa de cambio y la tasa de cambio porcentual del valor del inmueble dentro de 4 años.
Aplique la diferencial para calcular aproximadamente el incremento en el valor del inmueble en el primer trimestre del quinto año.

Problema nº) Calcule las tasas de cambio de la función de la demanda ![]()

Problema nº) Calcule las tasas de cambio de la función del interés continuo ![]()

Problema nº) Calcule las tasas de cambio de la función logística ![]()

Problema nº) El valor de una finca está dado por![]()
, donde t es el tiempo en años a partir del 1 de Enero del año 2000. Determine la tasa de cambio del valor de la finca el 1 de Enero del 2009.

Problema nº) El valor de una finca inmobiliaria está dado por ![]()
, donde t es el tiempo en años a partir del 1 de Enero del año 2005. Determine la tasa de cambio del valor de la finca pasados 5 años, el 1 de Enero del 2010.

Problema nº) El producto interior bruto (PIB) de un cierto país era ![]()
miles de millones de euros t años después del 1 de Enero de 2000.
¿A qué tasa cambiará el PIB con respecto al tiempo al final del año 2005?
¿A qué tasa porcentual cambiará el PIB con respecto al tiempo al final del año 2005?

Problema nº) Los datos que se tienen del PIB de un país europeo se ajustan a la siguiente función ![]()
miles de millones de euros t años después del inicio de 1990.
a) ¿A qué tasa cambiará el PIB con respecto al tiempo al inicio del año 2000?
b) ¿A qué tasa porcentual cambiará el PIB con respecto al tiempo al inicio del 2000?
c) Determine aproximadamente el incremento del PIB durante el tercer trimestre del año 2000.

Problema nº) El valor de una finca inmobiliaria está dado por ![]()
, donde t es el tiempo en años a partir del 1 de enero del año 2000. Determine la tasa de cambio del valor de la finca pasados 9 años, es decir el 1 de Enero del 2009.

Aplicación geométrica de la derivada
Problema nº) Dada la parábola de ecuación ![]()
. Halle el punto donde la recta tangente es paralela al eje de abscisas.

Tema 5
Máximos y mínimos
Problema nº) Una caja con tapa, de base cuadrada, debe tener un volumen de 250 centímetros cúbicos. El material de las partes inferior y superior de la caja cuesta 2 euros por ![]()
y el material de los lados de la caja cuesta 1 euro por ![]()
. Determine las dimensiones de la caja para que el coste de fabricación sea mínimo.




Problema nº) Dada la función de costes ![]()
donde ![]()
es el número de unidades producidas. Estudie los óptimos locales de la función de costes medios ![]()
.

Problema nº) El coste de una pieza manufacturada es de c euros, si se vende a x euros la pieza, se sabe que el número de piezas que pueden venderse es igual a:
![]()
Determine el precio de venta que produce el máximo beneficio.

Problema nº) Dada la función de costes ![]()
demuestre que la función de costes medio ![]()
tiene un mínimo en el intervalo ![]()
. Calcule dicho mínimo.


Problema nº) Suponga que la producción de x unidades de un artículo cuesta ![]()
euros. ¿En qué nivel de producción se minimizará el coste marginal?

Problema nº) Supóngase que producir “x” unidades de un artículo cuesta ![]()
miles de euros. ¿En que nivel de producción se minimizará el coste?

Problema nº) Los datos indican que t meses después de principios de año, el precio de una acción de Manufacturas metalizadas en la Bolsa es![]()
euros
a) Calcular el valor de t que hace que el precio sea mínimo.
b) Determinar el precio.

Problema nº) La función de demanda de las camisetas del jugador número 9 del equipo campeón de regional preferente es ![]()
, donde p representa el precio por unidad cuando se venden x camisetas. Si la función de costes total es ![]()
, determine:
¿Qué precio produce el máximo beneficio?
Halle el coste medio por unidad para la producción que hace máximo el beneficio.

Problema nº) Halle los extremos relativos de ![]()
para a=-3, b=2 y c=0.
![]()

Problema nº) El beneficio de una empresa viene dado por la función ![]()
, donde “x” representa el gasto de publicidad. A partir de esta función:
Calcule el gasto “x” de publicidad a partir del cual la empresa no tiene beneficios.
Determine los intervalos de crecimiento y decrecimiento de la función.
Calcule el valor de “x” que produce el máximo beneficio y averigüe la cuantía de éste.


Estudio de funciones
febrero de 2003 1º parcial
Problema nº) (Problema todavía sin resolver e incompleto) Considere la gráfica siguiente correspondiente a una función de costes C(x) y razone si las siguientes afirmaciones son verdaderas o falsas:
Mmmmmmmmmm
Mmmmmmmmmmmmmmmmmm
Los costes marginales crecen en ![]()
Los costes marginales decrecen en ![]()
El coste marginal es cero en x=a.
Los costes marginales no son negativos en ![]()
.
HHHHHHHHHHHHH
HHHHHHHHHHHh
febrero 2002 1º parcial
Problema nº) (Problema todavía sin resolver e incompleto) Dada la gráfica de la función ![]()
, estudie el crecimiento, decrecimiento, concavidad y convexidad de la función ![]()
.
HHHHHHHHHHHHHH
HHHHHHHHHHHHHHHH
28 enero 2004 parcial 1º
Problema nº) Conocida la gráfica de ![]()
estudie el crecimiento, decrecimiento, concavidad y convexidad de la función ![]()
.
mmmmmmmmmmmmm
HHHHHHHHHHHH
HHHHHHHHHHHHH
final 4 de septiembre 2002 1º y 2º parcial
Problema nº) (Problema todavía sin resolver e incompleto) Dada la gráfica de la función de producción F(x)
Mmmmmmmmmmmm mmmmmmmmmm m
Determine el crecimiento, decrecimiento, máximos y mínimos de la productividad marginal
HHHHHHHHHHHHHHH
HHHHHHHHHHHHh
septiembre 2005
Problema nº) (Problema todavía sin resolver e incompleto) Teniendo en cuenta la gráfica de la función f(x) representada en la figura, calcule el valor de
a) ![]()
b)![]()
c) ![]()
d)![]()
e) ![]()
f) ![]()
HHHHHHHHHHH
HHHHHHHHHHHH
Febrero 2005
Problema nº (Problema todavía sin resolver e incompleto)) Represente la gráfica de una función que sea discontinua en el punto x=0 y además sea negativa para x<0, positiva para cada x>0 y que cumpla ![]()
y ![]()
HHHHHHHHHHHHHH
HHHHHHHHHHHHHHHHHHHHHH
31 enero 2005 (1º parcial)
Problema nº (Problema todavía sin resolver e incompleto)) Dada la gráfica de ![]()
, indique:
Crecimiento y decrecimiento de la función f(x).
Concavidad y convexidad de la función f(x).
HHHHHHHHHH
HHHHHHHHHHHHHHHH
Problema nº) Halle los valores de los parámetros a, b, c y d para que la función ![]()
tenga un punto crítico en x=1, un punto de inflexión con tangente de ecuación y-x=0 en el origen de coordenadas.

Problema nº) Determine los valores de los parámetros ![]()
y ![]()
para que la función ![]()
pase por el punto (1,2) y la recta tangente a la gráfica de la función en el punto (1,2) sea ![]()
.

Problema nº) Halle los valores de ![]()
, ![]()
para que la gráfica de la función ![]()
pase por el punto (2,4) y la recta tangente a la curva en dicho punto sea y=2x.

Problema nº) Halle a, b, c y d para que la función ![]()
tenga un máximo en P(0,4) y un mínimo en Q(2,0)

Problema nº) Determine los coeficientes a, b y c para que la función![]()
, tenga un extremo relativo en el punto (0,0) y el punto (2,-16) sea un punto de inflexión.


Problema nº) Determinar los coeficientes, a, b y c para que la función![]()
, tenga un punto de inflexión en (2,10) y cuya recta tangente en este punto tenga pendiente 5.

Problema nº) Halle una función polinómica de tercer grado que pase por el punto (-1,1) y tenga un punto de inflexión con tangente horizontal en el punto (0,-2).


Problema nº) Determine los parámetros ![]()
y ![]()
para que la función ![]()
pase por el punto (2,4) y la recta tangente a la gráfica de la función en el punto ![]()
sea horizontal.

Problema nº) Encuentre los valores a, b y c para que la función ![]()
tenga un punto de inflexión de pendiente 18 en el punto (1,0).


Problema nº) Encuentre a, b y c para que la función ![]()
tenga un punto de inflexión en (1,2) y cuya recta tangente en dicho punto sea de pendiente 9.


Problema nº) Halle una función polinómica ![]()
que presenta un extremo relativo en el origen de coordenadas y otro en el punto (1,1).

Descargar
| Enviado por: | Jotamam |
| Idioma: | castellano |
| País: | España |
