Matemáticas
Matemáticas
INDICE
Página
I. Introducción 3
-
Objetivos
II. Generalidades 4
III. Desarrollo 5
-
Definición
-
Ejemplos
IV. Anexos 13
V. Conclusión 18
VI. Bibliografía 19
INTRODUCCIÓN
Para este trabajo elegimos el tema “numeración”, donde se encuentran los números reales (naturales, enteros, racionales e irracionales), números imaginarios o complejos.
Nuestro informe contará de las siguientes características:
-
Primero que todo plantearemos objetivos.
-
Presentaremos que partes del tema numeración profundizaremos en el trabajo.
-
En el desarrollo se podrá encontrar la definición general y detallada de cada subtema, además de ejemplos.
-
En la parte de anexos, pondremos ejercicios e informaciones adicionales.
-
Finalmente haremos una síntesis para lograr una conclusión y comprobar si los objetivos planteados fueron logrados satisfactoriamente.
OBJETIVOS
-
Conocer específicamente el tema numeración (Números reales, imaginarios y complejos).
-
Aplicar y aprender a resolver ejercicios con las propiedades de cada subconjunto de los números.
-
Aprender acerca de las personas que trataron estos temas en mayor profundidad.
GENERALIDADES
En nuestro trabajo trataremos los siguientes temas:
-
Definición de Números reales y números imaginarios (complejos).
-
Principales características de: Números reales (naturales, enteros, racionales e irracionales) y de los números imaginarios.
-
Personas que estudiaron estos números, haciendo aportes importantes.
-
Ejercicios.
DESARROLLO
-
Conjuntos numéricos o numeración:
Los números se dividen en grupos o conjuntos; donde cada uno contiene al anterior y es más completa que él y con mayores posibilidades en sus operaciones.
A continuación están los subconjuntos en un diagrama:
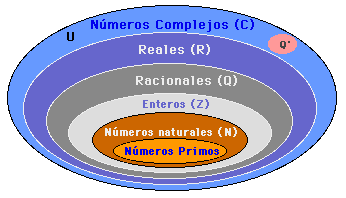
Figura 1. “Representación de conjuntos numéricos”
-
Números Complejos (C) o Imaginarios:
Estos números se usan mucho en matemáticas, física y electrónica, ya que facilitan los cálculos.
La estructura algebraica de los números complejos o imaginarios engloba a los Reales.
Los números complejos están compuestos de dos partes: una parte real y una parte imaginaria; cuando se extrae un resultado para aplicarlo a mediciones en la física, se toma sólo la parte real del número complejo.
Rene Descartes dio la designación de parte real y parte imaginaria, en 1833 Hamilton propuso la expresión:
a + ib
Con a y b reales. La letra i representa la raíz cuadrada de -1
Ejemplo:
7 + 5i - 8 + 4i - 20 - 6i
Propiedades importantes
Suma:
Multiplicación:
Para multiplicar este tipo de números se opera igual que con los reales:
z1 x z2 donde,
z1 = a + i x b y z2 = c + i x d
Con a,b,c y d reales. En este caso se opera como una multiplicación de dos binomios, pero tomando en cuenta las propiedades de i :
i = i
i2 = -1
i3 = -i
i4 = 1
i5 = i ………..
El resultado de la multiplicación es:
z1 x z2 = (a + i x b)(c + i x d)
= ac + i x ad + i x bc + i x b x i x d
= (ac - bd) + i x (ad + bc).
-
Números Irracionales (Q'):
Nacen por la necesidad de medir longitudes sobre algunas figuras geométricas.
La expresión decimal de cualquier número irracional consta de infinitas cifras no periódicas.
Existen infinitos números irracionales. Junto con los racionales forman el conjunto de los números reales.
Ejemplos:
![]()
-- ![]()
-- ![]()
Propiedad importante:
Tienen la importante propiedad de poder ser aproximados con el grado de precisión que se necesite.
-
Números Reales (R):
Se le denomina así a cualquier número que pertenezca a los racionales (Q) o a los irracionales (Q') .
Pueden expresarse de forma decimal, como número entero, decimal exacto, decimal periódico o no periódico.
Ejemplo:
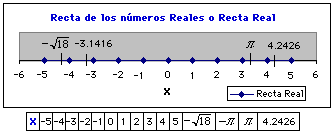
Figura 2. “Recta de los números reales o Recta Real”.
Las propiedades de los reales se presentan por separado en los números naturales, enteros, racionales e irracionales.
-
Números Racionales (Q):
Son los números que se pueden expresar como fracción.
De aquí nacen los números: Enteros y naturales.
Ejemplos:
7/45 -- 8/67 -- 98/45
Propiedades importantes
Suma:
La suma de números racionales tiene las mismas propiedades que la suma de números naturales y enteros. Tiene las propiedades conmutativa, asociativa, elemento neutro y existe el opuesto de cualquier número racional.
Asociativa
En una suma de números racionales pueden sustituirse dos o más sumandos por su suma ya efectuada, y no varía la suma total.
Ejemplo:
2/3 + (1/5 + 7/15) = 2/3 + 10/15 = 20/15
análogamente:
(2/3 + 1/5) + 7/15 = 13/15 + 7/15 = 20/15
Conmutativa
El orden de los sumandos no altera el valor de la suma.
Ejemplo:
2/3 + 1/5 + 7/15 = 1/5 + 7/15 + 2/3
20/15 = 20/15
Elemento neutro
En el conjunto de los números racionales existe un número que sumado a cualquier otro da siempre este otro. Este número se llama elemento neutro de la suma y es el cero.
Ejemplo:
3/4 + 0/6 = 9/12 = 3/4
Existencia del opuesto
El opuesto del número 3/7 es - 3/7
La suma de dos números opuestos pertenece a la clase del numerador cero.
Ejemplo:
4/7 + (- 4/7) = 0/4
Multiplicación
Asociativa
En un producto de números racionales pueden sustituirse dos o más de los factores por el producto efectuado.
Conmutativa
El orden de los factores no altera el producto.
Elemento neutro
En el conjunto de los números racionales existe un número que, multiplicado por cualquier otro, da siempre este otro. A tal número se le llama elemento neutro respecto del producto. Es el representado por las fracciones del tipo a/a (numerador y denominador iguales).
Elemento inverso
Es el que, multiplicado por un número racional, hace que su producto sea el elemento neutro.
Ejemplo:
Para 2/5 el inverso es 5/2 porque:
2/5 x 5/2 = 2 x 5/5 x 2 = 10/10
-
Números Enteros (Z):
Todos los números naturales y sus opuestos (negativos).
Ejemplos:
-4 -3 -2 -1 0 1 2 3 4
| | | | | | | | |
Representación de los números enteros en la recta numérica
Propiedades importantes
Suma:
Asociativa
(b + a) + c = a + (b + c)
Ejemplo: ((-3) + 22) + (-1) = (-3) + (22+(-1))
(1) + (-1) = (-3) + 3
0 = 0
Conmutativa
a + b = b + a
Ejemplo: 2 + (-3) = (-3) + 2
-1 = -1
Elemento neutro
En el conjunto de los enteros existe un número que sumado a cualquier otro, da siempre este otro. Este número se llama elemento neutro de la suma y es el cero.
Ejemplo: (-2) + 0 = -2 0 + 5 = 5
Notación de la suma
a.- Cuando sumamos números enteros de igual signo, el resultado es otro número entero del mismo signo.
b.- Cuando sumamos números enteros de distinto signo, el resultado lleva el signo del número de mayor valor absoluto.
Multiplicación:
Asociativa
(a x b) x c = a x (b x c)
Ejemplo: (-3 x 4) x -2 = -3 x (4 x -2)
-12 x -2 = -3 x -8
-
= 24
Conmutativa
a x b = b x a
Ejemplo: (-6) x 23 = 23 x (-6)
-48 = -48
Elemento neutro
El uno es un elemento neutro en la multiplicación de números enteros.
Producto por cero
El producto de cualquier número entero por el número cero es cero.
-
Números Naturales (N):
Los números naturales son los reales que son enteros positivos.
Los números naturales son infinitos.
Sirve para designar la cantidad de elementos que tiene un cierto conjunto.
Ejemplos:
8 -- 45 -- 63
Estos números tienen las mismas propiedades que los números enteros, pero sin usar el signo negativo, sólo números positivos.
Click en el hipervínculo para ver el cuadro comparativo entre los conjuntos numéricos:
Cuadro comparativo entre los conjuntos numéricos.doc
ANEXOS
Dentro de las siguientes páginas se podrán encontrar:
-
Datos relevantes de los temas tratados en el desarrollo, como por ejemplo, personajes destacados, utilizaciones de la numeración, etc.
-
Ejercicios resueltos, con desarrollo.
-
Ejercicios propuestos, con respuestas.
Personajes destacados
Rene Descartes (1596-1650)
Filósofo, científico y matemático francés, considerado el fundador de la filosofía moderna. Fue el primero en introducir a la matemática el concepto de “números complejos” y dio la designación de parte real e imaginaria a los elementos que componen un número complejo.
Utilizó las últimas letras del alfabeto para designar las cantidades desconocidas y las primeras letras para las conocidas.
Pierre de Fermat (1601-1665)
Matemático francés. Es especialmente recordado por sus aportes a la teoría de números, a la que contribuyó con la formulación de numerosos teoremas (en la mayoría de los casos no daba su demostración). Su mas famoso teorema es el llamado “Ultimo teorema de Fermat” .
Simón Stevin (1548-1620)
Matemático flamenco que introdujo por primera vez con claridad el concepto de fracción en la cultura occidental y, tomando como base el sistema decimal, propuso unificar, anticipándose a su tiempo, los sistemas de medidas, pesas y monedas.
Richard Dedekind (1831-1916)
Descubrió un proceso puramente aritmético para definir un numero irracional a partir del conjunto de los números racionales (método de las llamadas “Cortaduras” De Dedekind), sus ideas las publicó el año 1872, en un trabajo titulado “ Continuidad y números irracionales.
Datos importantes
-
Heinrich Schreiber Grammateus publicó una aritmética y álgebra tituladas Ayn new kunstlich buech en 1518. en dicho libro podemos comprobar como se había consolidado el uso del signo menos y el concepto de numero negativo, cuya introducción había sido mirada con desagrado por la iglesia su eventual carácter satánico.
-
El alemán Michael Stifel (1487-1567) , monje agustino convertido al protestantismo y amigo personal de Lutero, fue uno de los primeros en admitir el uso de coeficientes negativos para el estudio de las ecuaciones cuadráticas y divulgo el uso del signo menos para designar la resta.
EJERCICIOS RESUELTOS
Números complejos:
1.- (-3 + 4i) + (2 - 5i) = (-3 + 2) + (4 - 5) i = -1 - 1 i
2.- (9 + 3 i) + (2 - 4i) = (9 + 2) + (3 + (-4)) i = 11 - 1i
3.- (2 - 7i ) + (3 + 4i ) = (2 + 3) + ((-7) + 4) i = 5 - 3 i
4.- (1 + 8i ) + (2 - 3i ) = (1 + 2) + (8 + (-3)) i = 3 + 5 i
5.- (5 + 3i) + (7 + 2i) = (5 + 7) + (3 + 2) i = 12 + 5 i
6.- (4 + 3 i) + (5 + 9 i) = (4 + 5) + (3 + 9) i = 9 + 12 i
Números reales (racionales, enteros y naturales):
En estos ejercicios usaremos las siguientes operaciones : Suma, Resta, Multiplicación, división y potencia.
1.- (3/4 + 6/8) : (3/5) = 6 + 6/8 = 12/8 : 3/5 = 12/8 x 5/3 = 60/24 = 5/2 = 2,5
2.- (2/6 - 6/24) + (4/12 + 8/36) = (8 - 6/24) + (12 + 8/36) = (2/24) + (20/36) = 1/12 + 5/9 = 3 + 20/36 = 23/36 = 0,38
3.- 5,3 x 12,5 = 66,25
4.- (8 + 3/5) x (5/4)2 = (8 + 3/5) x (25/16) = (40+3/5) x (25/16) = (43/5) x (25/16) = 1075/80 = 13,4375.
5.- (8/20 x 5) + (- 8)2 = 40 /20 + 64 = 2 + 64 = 66.
6.- (5)3 x (-4)2 x (3)4 x (8)2 = 125 x 16 x 81x 64 = 10.368.000.
EJERCICIOS PROPUESTOS
Dentro de los ejercicios propuestos de números complejos y reales, se encontrarán las siguientes operaciones: Suma, resta, multiplicación, división y potencia.
1.- (-6 + 4 i) + (8 - 7 i) =
2.- (1/2 + 3/4 i) + (2/3 + 1/5 i) =
3.- (-5)3 + 82 - 92 + 72 =
4.- (1/4)-2 x (4/3)-3 =
5.- (3)0 x (10)2 + 46 x (-3)4 =
6.- (3 + 4 i) x (2 + 5 i) =
7.- 1/8 + 3/4 - (2/3 + 23) =
8.- 3,25 x 4,5 =
9.- 20x45+14/15+34-19 =
10.- (6/2)2 + (2/5)-2 =
RESPUESTAS
1.- 2 - 3 i
2.- 7/6 + 19/20 I
3.- -93
4.- 6,75
5.- 3.826
6.- -14 + 23 I
7.- -59/8
8.- 14,625
9.- 11,87
10.- 15,25
CONCLUSIÓN
A través de este informe se pudieron concretar satisfactoriamente los objetivos propuestos al inicio de este trabajo.
Esto se logró por medio de variada información, que fue ordenada y redactada por nosotros, conociendo así:
- Las propiedades más importantes de cada subconjunto numérico.
- Porque y como el hombre fue necesitando cada uno de estos tipos de números para sus usos en la vida diaria.
- Resolver ejercicios de números imaginarios, naturales, enteros, racionales e irracionales, utilizando las propiedades mencionadas en el desarrollo de nuestro informe.
- Conocimos importantes datos de la numeración y de personas que trabajaron con los diferentes números, deduciendo teoremas o mostrando formas de utilización.
BIBLIOGRAFÍA
-
Gran enciclopedia interactiva siglo XXI, editorial Océano, páginas 590 a la 627.
-
Enciclopedia Microsoft Encarta 2000.
19
z + w = (a + b i) + (c + d i) = (a + c) + (b + d) i
“Numeración”
Integrantes:
Curso: 2° medio.
Profesor:.
Fecha: 21.noviembre.2003
Números
Complejos
Números
reales
Números
Racionales
Números
Irracionales
Números
Enteros
Números
Naturales
Ejercicios
Personajes
destacados
NUMERACIÓN
Descargar
| Enviado por: | Viviana |
| Idioma: | castellano |
| País: | Chile |
