Ingeniero en Electrónica
Inductor sintético
PRACTICA 5
INDUCTOR SINTETICO
El objetivo de esta práctica es realizar un inductor sinté-tico, con el fin de determinar y comprobar su operación en forma práctica, este se comportará como un inductor, pero sería ridículo querer utilizar este inductor como devanado de excitación para un motor, ya que sólo es su respuesta lo que lo asemeja al inductor más no así sus propiedades electromag-néticas.
El oscilador sintético es un arreglo de amplificadores opera-cionales que simulan el efecto de un inductor, debido a que la relación de su impedancia es una factor de s y de un capacitor por un valor de R cuadrada.
Por supuesto que la respuesta de este arreglo de operaciona-les se reali- zará en base a la frecuencia, ya que no presentará la misma actividad que un inductor real bajo la presencia de CD. A su vez, debemos recordar que a mayores frecuencias se presenta el efecto de los capacitores de los operacionales , por lo que debemos trabajarlos en su región lineal de operación.
Los inductores que se presentan en esta práctica son inducto-res sintéticos expresados con respecto a masa, por lo que su relación de impedancia será su impedancia de entrada.
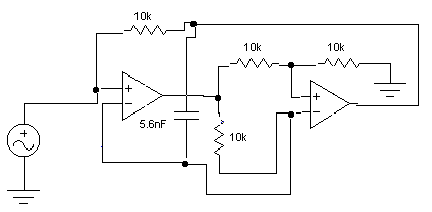
En el caso de la figura siguiente se presenta un inductor sintético girador el cual tiene la ventaja de poder permutar el capacitor con la resistencia R4 y su operación sigue siendo la misma.
Para la segunda figura el valor de Vi=V+ por lo que al estar en forma ideal Vd=0, con lo que V+=V- a partir de aquí realizamos el siguiente análisis
Vi/Ra=Ia Ra=R Ix=Ia+Ii
(v1-V2)/R=Ix
v2SC=Iy Ix=Iy+Ik Ik=(v2-v0)/R
Iy+Ik=Ia+Ii
V2SC + (V2-V0)/R= Vi/R + Ii
V2SC + 2Vi/R - V2/R= Vi/R + Ii
V2(SC-1/R)= Vi/R + Ii - 2Vi/R
Y como V2=Vi- Rix
(Vi-R(Vi/R+ Ii))((SCR-1)/R)=Ii-Vi/R
-Ii(SCR)=-Vi/R
Zi= Vi/Ii= SCR 2
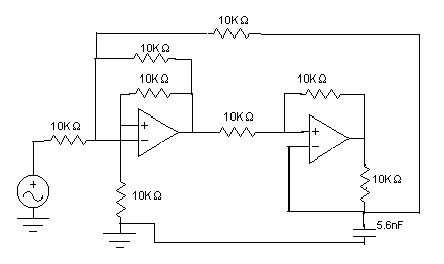
Para la primera figura observamos que v-=V+ y como el primero V+=Vi entonces como Vd=0 si el opamp se considera ideal por lo tanto V+=V-.
Ii=(Vi-Vo)/R IX=(Vi-Vo)SC
Y como la corriente que el opamp drena es prácticamente despreciable
Ix=Iy=Vi/R
Ii*R= Vi-Vo
Ix=Iy
Vi/R=(Vi-Vo=SC
Vi/R= Ii*RSC
Vi/Ii= SCR 2
Con esto ha quedado comprobado que en el caso de los dos circuitos, éstos se comportan como un inductor de valor CR2 .
GIRADOR
Así se le llama a una red eléctrica de dos puertos que puede realizarse conectando en paralelo y encontradas dos fuentes de corriente controladas por voltaje y de polaridades opuestas.
Se requiere mostrar que si el puerto 2 del girardor termina en una capacitancia, entonces el puerto de entrada tendrá la relación de una inductancia.
Se debe demostrar que en el circuito del girador
Vi=L(di/dt)
Donde L es una constante que representa una inductancia para obtener la relacición entre yl y vl, considerando el puerto 2 tenemos:
Vt=-(1/c)glvl dt
Donde se ha supuesto que c se encontraba originalmente sin carga
La corriente y1 se obtiene
Y= -GVI= (G1G2)/cVIDJ
Que puede escribirse en forma diferencial
VI=-C/G1G2*DI/DJ
Así la relación de i1-v1 es de la forma que se tiene en la inductancia l dada por
L=C/G1G2
Pudiendo utilizar el girador para realizar (sintéticamente hablando) una inductancia utilizando elementos activos (fuentes controladas) y una capacitancia.
DESARROLLO
Una vez que hemos llevado a cabo el análisis de los circuitos expuestos llamados inductores sintéticos hemos comprobado que el valor del inductor será equivalente a CR2 colocamos un C=5.6nF y como todas las resistencias son de 10 K, entonces:
L=CR2 =(5.6nF)(10K)2= 560mH
A su vez haciendo el análisis del filtro tenemos que:
Vo/Vi= sL/(sL+Ra) Ra=R
Colocando esto en la forma de Bode
Vo/Vi=(sL/R)(sL/R+1)
Con lo que vemos que el valor de w=R/L
W=R/L = 10K/560mH= 17Krad
De la función de transferencia observamos que si s=0
Vo/Vi=0
Y si s es infinito
Vo/Vi=1
Por lo que a frecuencia media la ganancia es casi unitaria, M(w)=1, comportándose así como un filtro pasa altas.
Descargar
| Enviado por: | Joel Rivera |
| Idioma: | castellano |
| País: | México |
