Ingeniero Industrial
Fundamentos físicos de la Ingeniería
INTRODUCCIÓN:
El objetivo de esta práctica es determinar con el mínimo de error posible, el diámetro de una esfera y la altura y diámetro de un cilindro. Para ello contamos con un pálmer y con un calibre. Una vez obtenidos los datos se realizará una tabla para una mejor comprensión de los resultados, teniendo en cuenta los errores. Posteriormente en el apartado de discusión se tratarán y se expondrán las conclusiones obtenidas de esta práctica.
DESCRIPCIÓN DE LA TÉCNICA EXPERIMENTAL:
La descripción de la técnica experimental se divide en dos partes: material a utilizar y procedimientos.
Material:
A continuación se describe los dos únicos aparatos necesarios para realizar la práctica: el calibre y el pálmer.
-Calibre o Pie de Rey:
El calibre es un aparato empleado para la medida de espesores y diámetros interiores y exteriores. Consta de una regla provista de un nonius.
El nonius es un aparato destinado a la medida precisa de longitudes o de ángulos. Se trata de una pequeña regla dividida en partes iguales que se desliza sobre la regla del calibre de tal forma que n-1 divisiones de la regla se dividen en n partes iguales del nonius.
Si cada división de la regla tiene por longitud un milímetro, y se han dividido nueve divisiones de ella en diez del nonius, la precisión es de 1/10 de mm (nonius decimal).
Cuando el calibre está cerrado deben coincidir exactamente los ceros de ambas escalas. Si esto no ocurriese hay que tenerlo en cuenta al realizar las medidas necesarias, restando o sumando el valor observado para obtener la medida exacta. Para medir una longitud se debe conocer su apreciación dada por la fórmula anterior. Se coloca el objeto en la posición, y se anota el número de divisiones hasta el cero de la escala móvil, y se busca la división de dicha escala que coincide con una división de la fija.
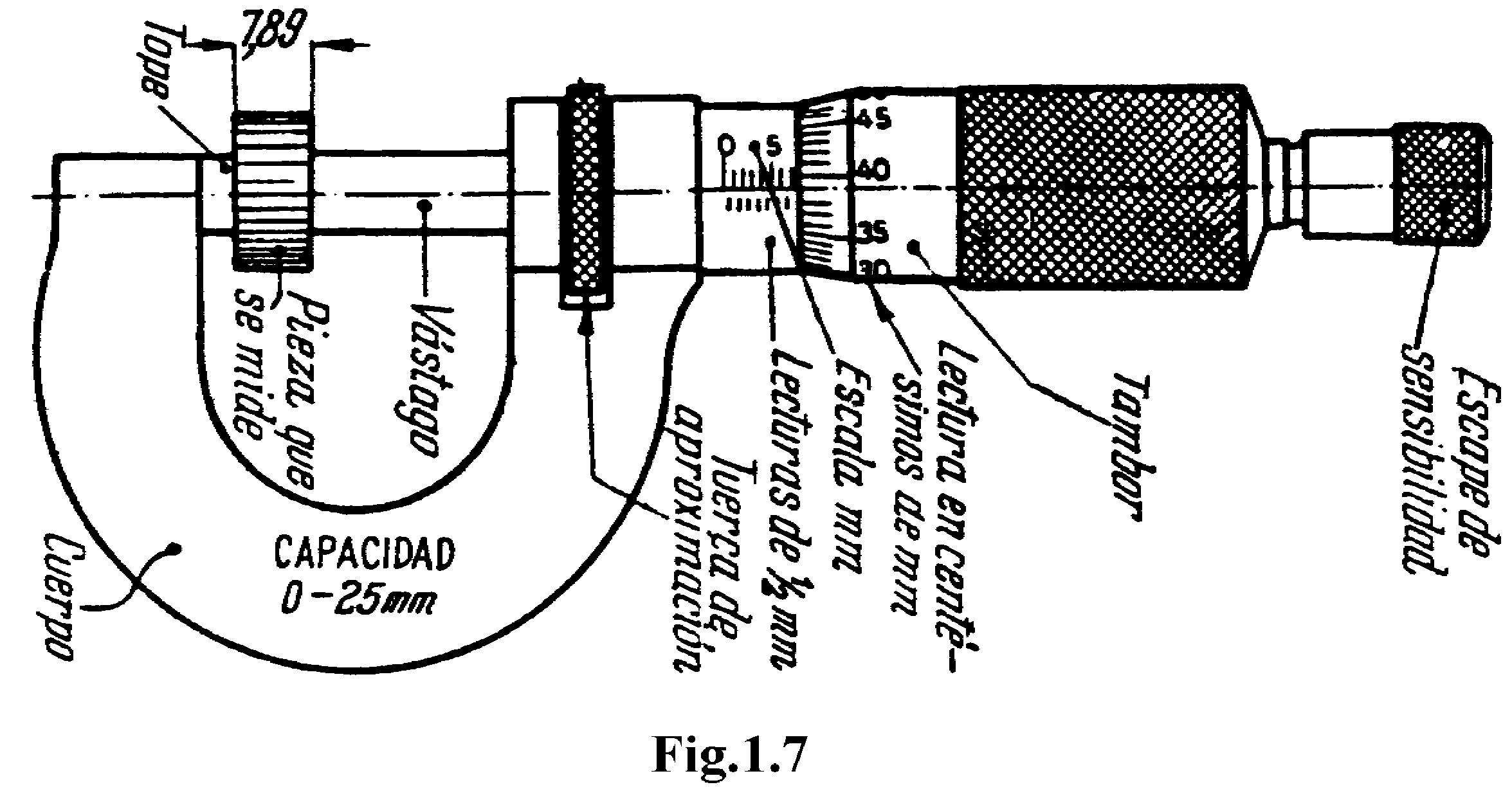
-Pálmer:
Este aparato está constituido por un cabezal en forma de “U”, un tubo metalizado graduado en mm y un rodillo giratorio también graduado. El pálmer dispone de una escala para apreciar el número de vueltas que da el tornillo, y éste tiene un tambor graduado que permite apreciar las fracciones de vuelta.
Para medir se coloca el objeto entre el tope y el extremo del tornillo y girando la cabeza de éste se presiona suavemente sobre el objeto. Para no forzar el tornillo se para cuando se escucha el “clic” del rodillo. Hay que utilizar ésta para realizar la medida. La regla marca el número de vueltas completas y se anota el número de fracción del rodillo que coincide con la horizontal en el eje.
Procedimiento:
Para este estudio se ha procedido a la toma de medidas de dos cuerpos: uno de forma esférica y otro con forma cilíndrica, mediante los aparatos adecuados.
Una vez conocidos los funcionamientos de los útiles de trabajo (ya explicado anteriormente) se procede a una descripción de los pasos llevados a cabo:
1º Comprobación de la correspondencia de las medidas indicadas con las medidas reales. Es decir, se ajusta el calibre y pálmer sin ningún objeto para comprobar que el 0 de la escala coincide con la ausencia de elemento.
2º Se mide 20 veces el diámetro de la esfera, el diámetro del cilindro y la altura del cilindro con el fin de evitar el error experimental. Cambiando además de posición los objetos a medir para tomar las medidas en distintos puntos y hacer una medición más fiable.
3º Elaboración de varias tablas (pág…..) donde se recogen los datos obtenidos. También se obtiene la media.
4º Ya obtenida la media se completan las tablas con varias columnas informativas que facilitaron la obtención de las restantes medidas de centralización y dispersión.
5º Sintetización de los datos reflejados en las tablas para obtener una conclusión. Además se aplicará el error cuadrático medio para abrir más el intervalo de fiabilidad.
RESULTADOS:
Seguidamente se muestra mediante tablas las medidas obtenidas en la práctica, además se han añadido más columnas para facilitar los cálculos de la media y la desviación típica. A los valores obtenidos de la media y la desviación típica, se le ha añadido el error cuadrático medio que se calcula por:
| Altura del cilindro | ||||
| N | Di | Di - D* | |Di - D*| | (Di - D*)2/10-3 |
| 1 | 18,3 | 0,257 | 0,257 | 66,049 |
| 2 | 18,5 | 0,457 | 0,457 | 208,849 |
| 3 | 18,1 | 0,057 | 0,057 | 3,249 |
| 4 | 17 | -1,043 | 1,043 | 1087,849 |
| 5 | 18 | -0,043 | 0,043 | 1,849 |
| 6 | 18,3 | 0,257 | 0,257 | 66,049 |
| 7 | 18,4 | 0,357 | 0,357 | 127,449 |
| 8 | 18 | -0,043 | 0,043 | 1,849 |
| 9 | 18,3 | 0,257 | 0,257 | 66,049 |
| 10 | 18,2 | 0,157 | 0,157 | 24,649 |
| 11 | 18,5 | 0,457 | 0,457 | 208,849 |
| 12 | 17 | -1,043 | 1,043 | 1087,849 |
| 13 | 18,06 | 0,017 | 0,017 | 0,289 |
| 14 | 18,2 | 0,157 | 0,157 | 24,649 |
| 15 | 18,2 | 0,157 | 0,157 | 24,649 |
| 16 | 18,3 | 0,257 | 0,257 | 66,049 |
| 17 | 18,1 | 0,057 | 0,057 | 3,249 |
| 18 | 17,3 | -0,743 | 0,743 | 552,049 |
| 19 | 18,2 | 0,157 | 0,157 | 24,649 |
| 20 | 17,9 | -0,143 | 0,143 | 20,449 |
| SUMA | 360,86 | 0 | 6,116 | 3666,62 |
Error cuadrático medio:
Media:
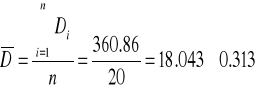
Desviación típica:
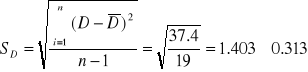
| Diámetro del cilindro | ||||
| N | Di | Di - D* | |Di - D*| | (Di - D*)2/10-6 |
| 1 | 14,91 | -0,006 | 0,006 | 36 |
| 2 | 15,01 | 0,094 | 0,094 | 8836 |
| 3 | 14,81 | -0,106 | 0,106 | 11236 |
| 4 | 14,95 | 0,034 | 0,034 | 1156 |
| 5 | 14,96 | 0,044 | 0,044 | 1936 |
| 6 | 14,94 | 0,024 | 0,024 | 576 |
| 7 | 14,99 | 0,074 | 0,074 | 5476 |
| 8 | 14,88 | -0,036 | 0,036 | 1296 |
| 9 | 14,86 | -0,056 | 0,056 | 3136 |
| 10 | 14,87 | -0,046 | 0,046 | 2116 |
| 11 | 14,79 | -0,126 | 0,126 | 15876 |
| 12 | 14,97 | 0,054 | 0,054 | 2916 |
| 13 | 14,94 | 0,024 | 0,024 | 576 |
| 14 | 14,97 | 0,054 | 0,054 | 2916 |
| 15 | 14,98 | 0,064 | 0,064 | 4096 |
| 16 | 14,99 | 0,074 | 0,074 | 5476 |
| 17 | 14,92 | 0,004 | 0,004 | 16 |
| 18 | 14,93 | 0,014 | 0,014 | 196 |
| 19 | 14,83 | -0,086 | 0,086 | 7396 |
| 20 | 14,82 | -0,096 | 0,096 | 9216 |
| SUMA | 298,32 | 0 | 1,116 | 84480 |
Error cuadrático medio:
Media:
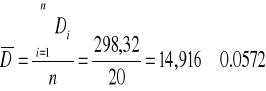
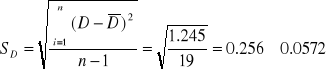
Desviación típica:
| Diámetro de la esfera | ||||
| N | Di | Di - D* | |Di - D*| | (Di - D*)2/10-6 |
| 1 | 20,01 | -0,0185 | 0,0185 | 342,25 |
| 2 | 20,1 | 0,0715 | 0,0715 | 5112,25 |
| 3 | 20,05 | 0,0215 | 0,0215 | 462,25 |
| 4 | 19,99 | -0,0385 | 0,0385 | 1482,25 |
| 5 | 20,03 | 0,0015 | 0,0015 | 2,25 |
| 6 | 20,02 | -0,0085 | 0,0085 | 72,25 |
| 7 | 20,03 | 0,0015 | 0,0015 | 2,25 |
| 8 | 20,02 | -0,0085 | 0,0085 | 72,25 |
| 9 | 20 | -0,0285 | 0,0285 | 812,25 |
| 10 | 20 | -0,0285 | 0,0285 | 812,25 |
| 11 | 20,04 | 0,0115 | 0,0115 | 132,25 |
| 12 | 20,03 | 0,0015 | 0,0015 | 2,25 |
| 13 | 20,02 | -0,0085 | 0,0085 | 72,25 |
| 14 | 20,01 | -0,0185 | 0,0185 | 342,25 |
| 15 | 20,06 | 0,0315 | 0,0315 | 992,25 |
| 16 | 20,08 | 0,0515 | 0,0515 | 2652,25 |
| 17 | 20,05 | 0,0215 | 0,0215 | 462,25 |
| 18 | 20,01 | -0,0185 | 0,0185 | 342,25 |
| 19 | 20,02 | -0,0085 | 0,0085 | 72,25 |
| 20 | 20 | -0,0285 | 0,0285 | 812,25 |
| SUMA | 400,57 | 0 | 0,427 | 15055 |
Error cuadrático medio:
Media:
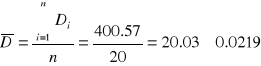
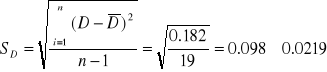
Desviación típica
CRITERIO DE CHAUVENET:
Mediante el Criterio de Chauvenet, que viene expresado por la siguiente fórmula:
SD = Desviación típica
En las tres tablas todos los valores fueron inferiores a K1 que según la tabla de valores tabulados a veinte medidas le corresponde el valor de 2.24 por lo que no desechamos ningún valor. Se demuestra en la siguiente tabla:
| N | Diámetro Esfera | Diámetro Cilindro | Altura Cilindro |
| 1 | 0,189 | 0,023 | 0,183 |
| 2 | 0,73 | 0,367 | 0,326 |
| 3 | 0,219 | 0,414 | 0,041 |
| 4 | 0,393 | 0,133 | 0,743 |
| 5 | 0,015 | 0,172 | 0,031 |
| 6 | 0,087 | 0,094 | 0,183 |
| 7 | 0,015 | 0,289 | 0,254 |
| 8 | 0,087 | 0,141 | 0,031 |
| 9 | 0,291 | 0,219 | 0,183 |
| 10 | 0,291 | 0,18 | 0,112 |
| 11 | 0,117 | 0,492 | 0,326 |
| 12 | 0,015 | 0,211 | 0,743 |
| 13 | 0,087 | 0,094 | 0,012 |
| 14 | 0,189 | 0,211 | 0,112 |
| 15 | 0,321 | 0,25 | 0,112 |
| 16 | 0,526 | 0,289 | 0,183 |
| 17 | 0,219 | 0,016 | 0,041 |
| 18 | 0,189 | 0,055 | 0,53 |
| 19 | 0,087 | 0,336 | 0,112 |
| 20 | 0,291 | 0,375 | 0,102 |
CONCLUSIÓN:
Tras todo el proceso se han obtenido las medidas más significativas de los elementos medidos.
A pesar de que los resultados se encuentran dentro del intervalo fiable, somos conscientes de que existe algún error en las tomas de medidas; ya que por el criterio de Chauvenet deberían haber sido apartadas algunas medidas puesto que se puede apreciar que los cuerpos a medir son bastante irregulares. Sin embargo, la medida obtenida es la más representativa de dichos cuerpos.
Se ha podido cometer ciertos errores que han podido variar los resultados obtenidos como puede ser:
1º: No tomar suficientes medidas ya que a más medidas tomadas, más se acercaría la media al valor real.
2º: Tomar las medidas en el mismo punto del cuerpo, esto influiría notablemente ya que se puede observar que los cuerpos son irregulares.
Descargar
| Enviado por: | Socorro |
| Idioma: | castellano |
| País: | España |
