Matemáticas
Funciones y números primos
UNA APROXIMACION DE LA FUNCION![]()
EN TEORIA DE NUMEROS
1.-Abstract
La funcion ![]()
en teoria de numeros nos da el numero de primos en un intervalo de 2 a x donde x es un numero real, la formulacin exacta de sesta funcion existe sin embargo tienen varios problemas como por ejemplo que son dificiles de computar o necesitas conocer todos los primos menores que el numero dado x.
En este documento pretendo dar una aproximación de esta funcion ![]()
usando para ello los metodos matematicos de la transformada de Laplace y la trasnformacion de Euler de una serie alterna, pienso que este metodo puede simplificar grandemente el problema para poder hallar una expresion de esta formula valida para todo x.
2.-Calculo de![]()
De la identidad:
![]()
Donde la suma esta tomada sobre todos los primos y con f is diferenciable para todo R substituyendo f(x) =exp(-sx) con Re(s)>0 tendriamos::
(2) 
O de la definicion de la Transformada de Laplace:

Si pudiesemos calcular la suma anterior podriamos resolver ![]()
haciendo la transformada inversa desgraciadamente esta suma es dificl de calcular para hallar una aproximacion usaremos la transformacion de Euler de una serie alterna::

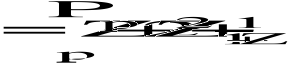
![]()
La funcion ![]()
vale 0 o 1 dependiendo de si n es primo o compuesto y (-1)p is -1 para todos los primos excepto 2 y tenemos que el termino an>0 para todo n asi que aplicando la transformación de Euler:

![]()
En este caso a0=1
Donde se ha definido el operador derivada fraccionaria como sigue: ![]()
, ![]()
Poninedo Z=exp(-s) en Nuestra trasnformada de Euler tendriamos:
::

![]()


![]()
Donde la funcion E(s) esta definida como::
![]()
![]()
![]()
Donde L-1 es la transformada inversa de Laplace:

And finally we have ![]()
Where we have called R(s) to the function
![]()
![]()
Una variacion de este metodo podria servirnos para calcular sumatorios sobre primos para cualquier funcion f(x) simplemente si cogemos la serie:

![]()
Haciendo ahora Z=1



Aplicando ahora Z=1 en nuestra transformacion de Euler tendremos:

![]()
Asi que hemos conseguido calcular la serie ![]()
para cualquier f:
La eleccion de la transformada de Euler se debe a que sirve para mejorar la convergencia de la s series alternadas y que bastan unos pocos terminos de la serie aplicando dicha transformación para calcular su suma de manera aproximada asi que relamente con unos pocos valores de ![]()
bastarian para calcular la suma aproximada de exp(-sp) para todos los primos p.
Otro uso de este metodo seria para calcular la funcion B(n) que es la funcion característica de los primos:
b(n)=0 sii n es compuesto b(n)=1 sii n es primo.
Sabemos que ![]()
siendo este B(n):
![]()

A partir de conocer B(n) para todo n representadola podriamos saber cuando B(n) =1 siendo en este caso el n un numero primo.
Descargar
| Enviado por: | Eljose |
| Idioma: | castellano |
| País: | España |
