Matemáticas
Función logarítmica y exponencial
Índice
-
Introducción pág.2
-
Un poco de historia pág.2
-
Potencias, logaritmos y su relación pág.4
-
Función pág.6
-
Función inversa pág.6
-
Función exponencial pág.7
-
Representación gráfica de la función exponencial pág.8
-
Ejemplos de funciones exponenciales pág.9
-
Exponenciales expresadas como potencias de e pág.9
-
Definición de ex para x real cualquiera pág.10
-
Ecuaciones y sistemas de ecuaciones exponenciales pág.11
-
Función logarítmica pág.12
-
Representación gráfica de la función logarítmica pág.12
-
Bibliografía pág.13
Introducción
El concepto de función es tan extenso y tan general que no es sorprendente encontrar una inmensa variedad de funciones que se presentan en la naturaleza. Lo que sí es sorprendente es que un corto número de funciones especiales rijan una multitud de fenómenos naturales totalmente diferentes.
Estudiaremos aquí algunas de estas funciones, o sea la función exponencial y su inversa, la función logarítmica.
Es importante para todo aquel que estudie Matemática, ya sea como una disciplina abstracta o como instrumento en otros dominios científicos, tener un conocimiento práctico y teórico de estas funciones y sus propiedades.
Para comprender más extensamente estas funciones hemos de remontarnos un poco y repasar algunas definiciones, como ser la de exponenciación, logaritmo y función; así como algunas de sus propiedades más relevantes.
Un poco de historia
El estudio del movimiento fue el problema que más interesó a los científicos del siglo XVII, influidos por los descubrimientos de Kepler y Galileo en relación con los cuerpos celestes.
A este gran interés también contribuyeron motivaciones de carácter económico y militar, del mismo modo que en la actualidad.
Respecto del primer motivo, los navegantes europeos, en su búsqueda de materias primas y de nuevas relaciones comerciales, se alejaban cada vez más de las costas de las que partían y esto les ocasionaba grandes dificultades para conocer su posición en alta mar y llegar al lugar deseado. Necesitaban saber la latitud y la longitud (coordenadas terrestres); la primera se conseguía por observación directa del Sol o de las estrellas; pero la segunda ofrecía serias dificultades porque no disponían de los medios adecuados para medir correctamente la dirección del movimiento de la Luna, y cometían numerosos errores.
Los gobiernos de Europa estaban muy interesados en solucionar este problema porque se producían cuantiosas pérdidas económicas. Por ello se estimulaban a los científicos a que construyeran tablas de datos cada vez más aproximados.
En relación al segundo motivo, las trayectorias de los proyectiles, sus alcances y alturas, el efecto de la velocidad de la boca del arma cobre ellos eran asuntos de sumo interés para los gobernantes, por lo que invertían grandes sumas de dinero para financiar la búsqueda de soluciones satisfactorias.
Del estudio de diversos problemas del movimiento se extrajo la conclusión de que era necesario medir el tiempo con mayor precisión, y se llegó a vincular este problema con el movimiento del péndulo, mecanismo básico para la medida del tiempo.
La carencia de instrumentos de medida suficientemente precisos para construir tablas de variables impidió que el estudio de este concepto se abordara antes. Por ejemplo, los griegos, que en otros aspectos tenían un desarrollo matemático admirable (recordemos el libro Los elementos de Euclides que ya en el siglo III a.C. recogía toda la geometría de su tiempo), no llegaron a tener una idea del movimiento lo suficientemente elaborada.
De los anteriores estudios, obtuvieron los matemáticos un concepto fundamental, que fue central en casi todo el trabajo de los dos siglos siguientes: el concepto de función o de relación entre variables.
El concepto de función aparece explícitamente en Leibniz(1692), y es utilizado por los Bernoulli desde 1694. Euler(1707-1783) introdujo en 1734 el símbolo f (x). Al concepto general de función algebraica, incluso no expresable por radicales, fue claramente definido por Euler, quien llamaba trascendentes a las funciones definidas por algoritmos indefinidos, lo que no es correcto; pero debe sobrentenderse que se refiere a las funciones definidas por series potenciales y que no son algebraicas.
El concepto bernoulliano y euleriano de variable y dependiente de x, o función de x, coincidía con el de expresión aritmética formada con la variable x, y ciertos números fijos o constantes. La palabra continua significa para Euler función dada por una sola expresión.
El problema de la cuerda vibrante, resuelto por D'Alembert (1747), introdujo a Euler a admitir funciones arbitrarias definidas gráficamente, puesto que la forma inicial de la cuerda puede ser arbitraria. Por otra parte, dio Bernoulli una expresión por serie trigonométrica a la forma de la cuerda en todo momento, y en vista de ello hubo que suprimir esa distinción entre función matemática y función arbitraria, ya que también éstas son expresables por las operaciones aritméticas. Todo esto condujo a prescindir del modo de dar la correspondencia entre los valores de x y los de y, para atender solamente a la correspondencia en sí misma, y así quedó establecido por Dirichlet el concepto general de función (1854) como correspondencia arbitraria entre dos variables.
Potencias, logaritmos y su relación
El producto de n factores iguales a a: n
a · a · ... · a, se llama potencia de base a y exponente n, donde a ð 0 ó n ð 0.
Es de suponer que no sea una operación conmutativa, ya que base y exponente cumplen funciones distintas. (La demostración queda conforme con sólo ver que 23 ð 32).
Algunas propiedades son:
-
a0 = 1; 00 no tiene sentido.
-
El producto de potencias de igual base es una potencia de la misma base que tiene por exponente la suma de los exponentes.
n m n+m
an · am = a · a · ...· a · a · a · ...· a = a · a · ...· a = an+m
-
El producto de potencias de igual e ponente es igual a una potencia del mismo exponente que tiene por base el producto de las bases.
n n n
an · bn = a · a · ...· a · b · b · ...· b = (a · b) · (a · b) ·...· (a · b) = (a · b)n
n n
-
(am)n = am · am · ...· am = am+m+m+...+m = amn
-
an : am = an - m
-
an : bn = (a : b)n
Es importante observar que la potenciación, como consecuencia de no tener propiedad conmutativa, da origen a dos operaciones inversas. Hemos de recordar que operaciones como la adición y la multiplicación ofrecen sólo una operación inversa, respectivamente la sustracción y la división, como consecuencia directa de la propiedad conmutativa.
En la potenciación observamos dos operaciones inversas que explicitan respectivamente la base y el exponente:
Radicación: Si b es potencia enésima de a podemos expresar la base como que a es la raíz enésima de b.
Logaritmación: n = loga b, es un número tal que an = b. Con a>0, b>0 y b ð 1.
Algunas de sus propiedades son:
-
Si c>0, es a logac =c
-
Si c>0 y c'>0, es: loga(c·c') = logac + logac'. En efecto, siendo c y c' positivos, se cumple:
c = a logac y c'= a logac' .·. c · c' = alogac · alogac = alogac + logac'
.·. loga(c · c') = logac +logac'.
-
Si c>o y c'>0, es: loga(c:c') = logac - logac'.
En este caso dividimos:
c : c' = alogac : alogac = alogac - logac'
Corolario: loga1/c = loga1 - logac y, como loga1 = 0, resulta: loga1/c = -logac.
-
Si c>0, es logacd = d logac.
En efecto, siendo: c = alogac, es también: cd =(alogac)d = ad logac .·. logacd = d logac.
-
logac = logbc / logba.
Función
Cada función consta de tres elementos:
Dominio de definición: conjunto de objetos cualesquiera, en nuestro caso, números reales.
Una ley de correspondencia que nos permite asociar un elemento del dominio de definición con uno del recorrido.
Recorrido: conjunto en el cual se encuentran los correspondientes objetos del dominio.
Dominio Recorrido
Conjunto de reales o parte de él Conjunto de los reales o parte de él
x variable independiente y variable dependiente
Si tenemos un conjunto A de números reales, y a cada número a del conjunto A le asignamos un correspondiente b, decimos que se ha definido una función en el conjunto A. Es pues, ésta una correspondencia unívoca; a cada elemento a se le asigna un b, y para evidenciarlo se escribe b= f (a).
Función inversa
Una función es:
Inyectiva, si para x1 ð x2 se cumple que f(x1) ð f(x2).
Sobreyectiva, si cualquier elemento de R es imagen de un elemento de D.
Cuando la función f(x) cumple estas condiciones, existe la función inversa de la f, cuyo dominio es R y cuyo recorrido el D. La función inversa es además inyectiva y sobreyectiva.
Sea y un elemento de R; por 1. y 2., le asociamos el elemento de D que existe por 2. Esta correspondencia es la función inversa buscada.
Así es que dos funciones y= f(x) e y= ð(x) se llaman inversas entre sí, si para cada par de valores (a, b) que verifican la condición b= f(a), se verifica también la condición a= ð(b), y viceversa. Una de las dos funciones inversas entre sí se puede llamar directa (es indiferente cual de ellas); entonces la otra se llama inversa con respecto a la primera.
Para obtener una inversa de una función directa y= f(x), se deben cambiar de lugares el argumento y la función; la ecuación x= f(y) determina implícitamente la función inversa a y= f(x). Resolviendo x= f(y) con respecto a y se obtiene en forma explícita la función inversa y= ð(x).
Las gráficas de las funciones directas e inversas son simétricas con respecto a las bisectrices de los ángulos del primero y tercer cuadrantes.
Función exponencial
Se llama así a la función y= f(x) = ax, cuando a>0, es decir una potencia donde la variable independiente es el exponente, siendo la base una constante positiva.
Tendremos, por ejemplo, f(3/2)= a3/2. Tomando la raíz aritmética, la función queda unívocamente definida para todo x racional, y su variación en este campo resulta de lo siguiente:
Las potencias de exponente racional de los números positivos mayores(menores) que uno, son mayores(menores) que uno si el exponente es positivo, y son menores(mayores) que uno si es negativo. En ambos casos crecen(decrecen) al crecer el exponente.
Si a=1, se reduce a la función constante f(x) =1 y no la consideramos como función exponencial.
Con lo establecido anteriormente, podemos enunciar las siguientes propiedades de la función exponencial:
Para todo x es ax>0. En particular, la función exponencial no se anula nunca.
f(0) = a0 =1. [Todas las gráficas pasan por el punto (0, 1)]
f(1) = a1 = a.
Para a>1 (es decir, b>0) es monótona creciente desde 0 hasta ð; para a<1(es decir, b<0) es monótona decreciente desde ð hasta 0, tanto más rápidamente cuanto mayor sea ð bð .
lim ax = + ð (a>1) lim ax = 0 (0<a<1)
x →ð ð x →ð ð
La curva se aproxima asintóticamente al eje x(para b>0 a la izquierda, para b<0 a la derecha), tanto más rápidamente cuanto mayor sea ð bð .
lim ax = 0 (a>1) lim ax = +ð (0<a<1)
x →ð ð x →ð ð
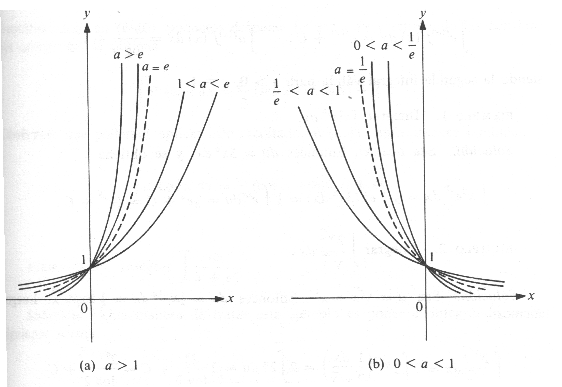
Representación gráfica de la función exponencial
Ejemplos de funciones exponenciales
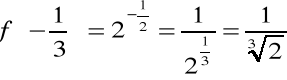
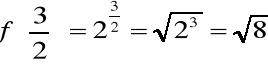
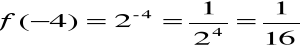
1. La función y = 2x es una función exponencial de base 2. Algunos de los valores que toma esta función, f: R R, son:
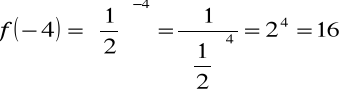
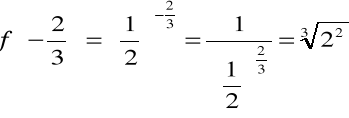
![]()
2. La función y= 1/2x es una función exponencial de base 1/2. Algunos de los valores que toma esta función son:
Exponenciales expresadas como potencias de e
La ecuación funcional E(a +b) = E(a)E(b) tiene muchas consecuencias interesantes. Por ejemplo podemos utilizarla para demostrar que
(1) E(r) = er
Para todo número racional r.
Tomamos primero b= -a en la ecuación funcional obteniendo
(2) E(a)E(-a)=E(0)=1,
y por lo tanto E(-a)=1/E(a) para todo a real. Tomando b= a, b= 2ª, . . ., b= na en la ecuación funcional obtenemos, sucesivamente, E(2 a)= E(a)2, E(3 a)= E(a)3, y, en general,
(3) E(na)= E(a)n
para todo n entero positivo. En particular, cuando a=1, obtenemos
(4) E(n)= en,
mientras que para a= 1/n, se obtiene E(1)= E(1/n)n. Puesto que E(1/n)>0, ello implica
(5) E(1/n)= e1/n.
Por consiguiente, si ponemos a= 1/m en (3) y aplicamos (5), encontramos
E(n/m)= E(1/m)n= en/m
para m y n enteros positivos cualesquiera. Dicho de otro modo, hemos demostrado (1) para cada número racional positivo. Como E(-r)= 1/E(r)= e-r, también es válida para todo r racional negativo.
Definición de ex para x real cualquiera
En el apartado anterior se ha probado que ex = E(x) cuando x es un racional cualquiera. Ahora se definirá ex para x irracional por
(7) ex = E(x) para cada x real.
La máxima justificación que se puede dar de esta definición es que con ella la ley de los exponentes
eaeb= ea+b
es válida para todos los números reales a y b. Cuando se toma la definición (7), la demostración de (8) es trivial puesto que (8) no es más que la misma afirmación de la ecuación funcional.
Se ha definido la función exponencial de manera que las dos ecuaciones
y= ex y x= ln y signifiquen exactamente lo mismo.
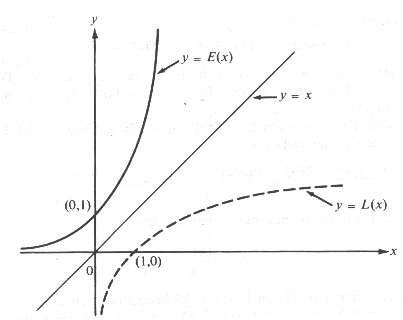
La gráfica de la función exponencial y= ex la obtenemos de la del logaritmo y=L (x) por una simetría respecto a la recta y= x.
Ecuaciones y sistemas de ecuaciones exponenciales
Las ecuaciones en las que la incógnita aparece como exponente son ecuaciones exponenciales.
No existe fórmula general alguna que nos muestre cómo resolver todas las ecuaciones exponenciales. Sólo a través de la práctica podremos determinar, en cada caso, qué camino tomar.
Para resolver estas ecuaciones hay que tener presente algunos resultados y propiedades que ya se han descrito anteriormente.
Ejercicio: resolución de ecuaciones exponenciales
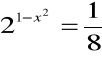
1. Resolver
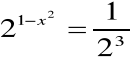
Resolución:
![]()
Expresando 1/8 como potencia de 2:
Basta ahora con resolver esta ecuación de segundo grado: 1 - x2 = -3 → x2 = 4 → x = ± 2
2. Resolver 4x+1 + 2x+3 = 320
Resolución:
En algunas ecuaciones es necesario hacer un cambio de variable para su resolución. Teniendo en cuenta las propiedades de las potencias, la ecuación puede escribirse:
4 · 4x + 23·2x = 320 → 4 · 4x + 8·2x = 320
Expresando 4x como potencia de dos, 4 · 22x + 8 · 2x = 320
Se hace el cambio de variable 2x = y, (por tanto 22x = y2) y se obtiene: 4y2 + 8y = 320
Basta ahora con resolver esta ecuación: y2 + 2y - 80 = 0

Se deshace ahora el cambio y = 2x
y1 = -10 = 2x. No es posible encontrar un x que verifique esta condición (2x es siempre positivo)
y2 = 8 = 2x → x = 3
La solución es, por tanto, x = 3
3. Resolver 5x + 5x+2 + 5x+4 = 651
Resolución: Aplicando las propiedades de las potencias, la ecuación se puede escribir como
5x + 52 ·5x + 54 ·5x = 651
Sacando factor común 5x:
5x (1 + 52 + 54) = 651 5x·651 = 651 → 5x = 1 → x = 0
Función logarítmica
Se llama así a la función inversa a la exponencial, que existe en base a lo demostrado anteriormente:
x = ð (y) = loga y, definida para 0<y<+ð, si a>0 y að1.
Escribamos ahora la función de otra forma:
y = ð (x) = loga x,
donde llamamos de nuevo x a la variable independiente e y a la función, y obtenemos de la gráfica de la función exponencial, la gráfica de la función logarítmica por simetría de primer y tercer cuadrantes.
Por las propiedades de los logaritmos vistas previamente enunciamos las siguientes:
La función logax sólo está definida para x>0.
logaa =1 y loga1=0. [Todas las gráficas pasan por el punto (1, 0)]
Para a>1 (es decir, b>0) es monótona creciente desde -ð hasta +ð; para a<1 (es decir, b<0) es monótona decreciente desde +ð hasta -ð, tanto más lentamente cuanto mayor sea
ð loga xð .
lim logax = + ð (a>1) lim logax = ðð (0<a<1)
x →ð ð x →ð ð
La curva se aproxima asintóticamente al eje y(para a>1 hacia abajo, para a< 1 hacia arriba), tanto más rápidamente cuanto mayor sea ð logaxð .
lim logax = ðð (a>1) lim logax = +ð (0<a<1)
x →0ð x →0+
Representación gráfica de la función logarítmica
Bibliografía
-
Introducción al análisis matemático; Luis Osín.
-
Calculus, Volumen I; Tom M. Apostol.
-
Manual de matemáticas para ingenieros y estudiantes; I. Bronshtein, K. Semendiaev.
-
Aritmética 3; C. Repetto, M. Linskens, H. Fesquet.
-
Análisis matemático; Tom M. Apostol.
-
Análisis matemático, Volumen I; J. Rey Pastor, P. Pi Calleja, C. A. Trejo.
-
Matemáticas 3; C. Amigo, P. Peña, A. Pérez, A. Rodríguez, F. Sivit.
-
Apuntes de análisis matemático II(del curso del profesor F. Forteza); A. Dieste, C. Pfeif.
-
Apuntes de análisis matemático(de las clases del profesor R. Ciganda); Santiago Michelini.
-
Problemas y ejercicios de análisis matemático; B. Demidovich.
1
- 9 -
![]()
![]()

![]()

![]()
![]()



![]()

Descargar
| Enviado por: | Acy |
| Idioma: | castellano |
| País: | Uruguay |
