Matemáticas
Examen de Selectividad de Matemáticas
OPCIÓN A
A1. PROGRAMACIÓN LINEAL.
| Variedades |
Publicidad | |
| Programa 1 | 20x | 1x |
| Programa 2 | 10y | 1y |
| 80 | 6 |
Restricciones 20x+10y![]()
x+y![]()
x,y>0
Función objetivo f(x,y) = 30000x+10000y
A2. FUNCIONES
Es una función racional, por tanto, su dominio es toda la recta real excepto los puntos donde se anula el denominador.
Se resuelve la euación x2+2x-3=0 y salen por soluciones x=1, x= -3
Conclusión Dominio= ![]()
Asíntotas: Tiene asíntotas verticales y horizontales.
A.Verticales: x=1, x=-3
Demostración:
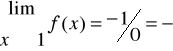
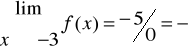
Horizontal:
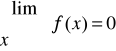
; por tanto y=0 es una Asíntota horizontal.
A3. Integración y representación
1º) Estudio las raíces de la función y=3x2+2x-16
Las raíces son 2, -2`6 .
2º) Estudio el signo de la función
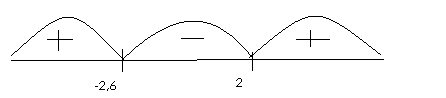
Como me piden el área entre x=-2 y x=4:
Área = 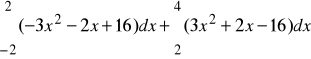
= 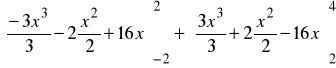
y aplico la Regla de Barrow.
Esbozo del área: Este dibujo sería la gráfica de “y”, habría que rayar la zona entre -2 y 4, y ese es el área pedida.
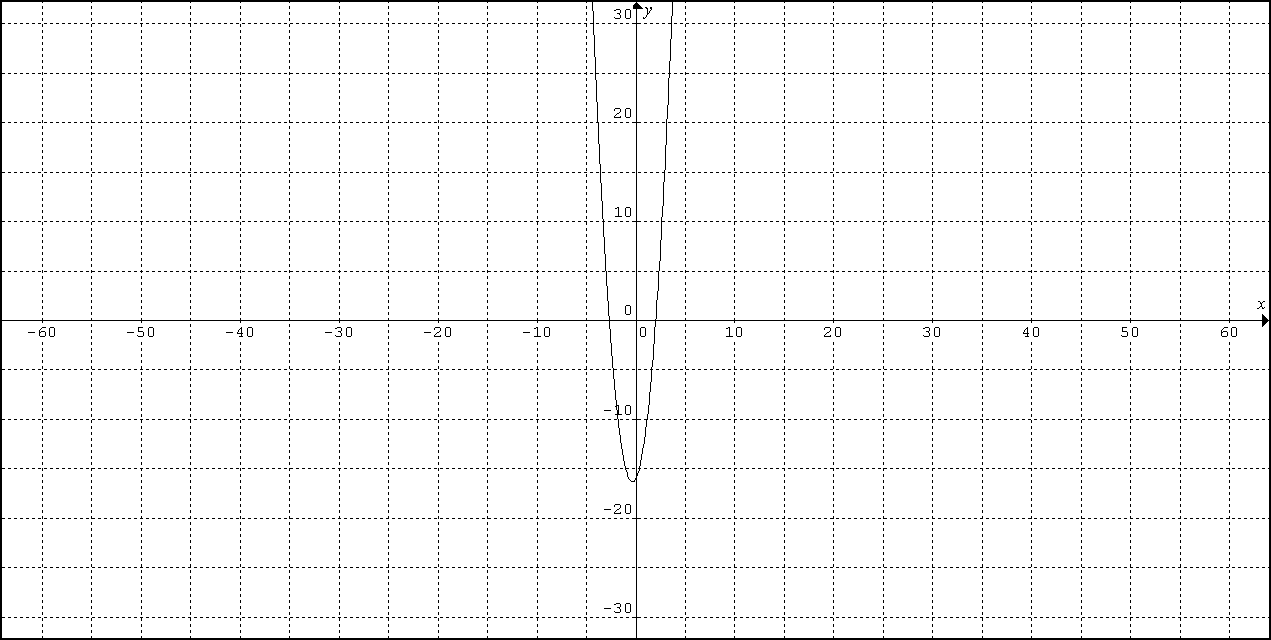
A.4. PROBABILIDAD
D: defectuoso

P(Defectuoso) = Aplico el Teorema de la Probabilidad Total= ![]()
= 0,5·0,5+ 0,25·0,25+0,16·0,25
A.5. ESTADÍSTICA E INFERENCIA.
Piden el intervalo de confianza para la media a un 99% de confianza.
n=100
media muestral= ![]()
Varianza= 576
Desviación: raiz de varianza= 24
1º) por el Teorema central del límite

![]()
2º) El intervalo de confianza es :

Se busca k(que deja por debajo 0,995 de probabilidad en una normal ) y k= 2,57
Se estima la media con la media muestral y obtenemos:
![]()
( 198`83 , 211`168 )
Descargar
| Enviado por: | María José |
| Idioma: | castellano |
| País: | España |
