Matemáticas
Análisis matemático y Geometría
1.- a) Relación entre continuidad y derivabilidad.(1,5 PTOS)
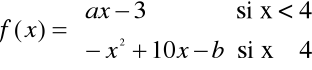
b) Hallar a y b para que la función f(x) cumpla las hipótesis del teorema del valor medio del cálculo diferencial en el intervalo [2,6], ¿dónde cumple la tésis? (1,5 PTOS)
2.- Dada la función 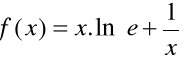
se pide:
a) Calcular ![]()
b) Hallar las asíntotas de la curva y = f(x). (2 PTOS)
3.- Calcular las siguientes integrales:
4.- Calcular el área del recinto determinado por las siguientes funciones:
1.- a) Relación entre continuidad y derivabilidad.(1,5 PTOS)
b) Hallar a y b para que la función f(x) cumpla las hipótesis del teorema del valor medio del cálculo diferencial en el intervalo [2,6], ¿dónde cumple la tesis? (1,5 PTOS)
2.- Dada la función 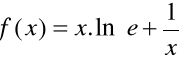
se pide:
a) Calcular ![]()
b) Hallar las asíntotas de la curva y = f(x). (2 PTOS)
3.- Calcular las siguientes integrales: (1,5 PTOS)
4.- Calcular el área del recinto determinado por las siguientes funciones:
(2 PTOS)
5.- Teorema fundamental del cálculo integral: Enunciado, interpretación geométrica y demostración. (1,5 PTOS)
1.- Hallar los limites siguientes:
Solución: -1 Solución: 1.5
Solución: 2 Solución: 1
2.- Estudiar la continuidad de la siguiente función:
3.-Demostrar que la ecuación x = cosx tiene una soluciòn en el intervalo (0,1).
4.-Hallar la ecuación de la tg. a la curva en el punto P(1.11).
Solución: y = 6x + 5
5.- Comprobar utilizando los teoremas de BOLZANO Y ROLLE que la curva ![]()
tiene tres puntos de intersección con el eje OX.
6.- Representar gráficamente la función
1.-Hallar “k” para que la función ![]()
tenga en x = 2 una recta tangente que forme 45º con el eje OX.
2.- Estudiar si la función![]()
cumple las condiciones de los teoremas de ROLLE y del VALOR MEDIO en el intervalo [-1,1].
3.- Hallar los límites:
4.- Hallar los intervalos de crecimiento y decrecimiento de:
5.- La función ![]()
es continua en [-1,1] y f(1) = f(-1) pero f´(x) no se anula para ningún punto perteneciente [-1,1]. Explicar la aparente contradicción del teorema de ROLLE.
1.- Comprobar que no puede existir un triángulo con :
Â=30º a = 3cm. B= 8cm.
2.- Resolver el sistema:
senx +seny =![]()
cosx +cosy = 1
3.- Pasar a forma polar: 4.- Calcular el valor de:
5.- Resolver las integrales:
-
6.- Calcula el área comprendida entre:
7.- Ecuación de la recta que pasa por (1,3) y forma 60º con 4x-y=6
8.- Calcula el área del triángulo. (radio R=2):
Descargar
| Enviado por: | Ardeme |
| Idioma: | castellano |
| País: | España |
