Administración y Dirección de Empresas
Estadística
Estadística:
La estadística es comúnmente considerada como una colección de hechos numéricos expresados en términos de una relación sumisa, y que han sido recopilado a partir de otros datos numéricos.
Kendall y Buckland (citados por Gini V. Glas / Julian C. Stanley, 1980) definen la estadística como un valor resumido, calculado, como base en una muestra de observaciones que generalmente, aunque no por necesidad, se considera como una estimación de parámetro de determinada población; es decir, una función de valores de muestra.
"La estadística es una técnica especial apta para el estudio cuantitativo de los fenómenos de masa o colectivo, cuya mediación requiere una masa de observaciones de otros fenómenos más simples llamados individuales o particulares". (Gini, 1953.
Murria R. Spiegel, (1991) dice: "La estadística estudia los métodos científicos para recoger, organizar, resumir y analizar datos, así como para sacar conclusiones válidas y tomar decisiones razonables basadas en tal análisis.
"La estadística es la ciencia que trata de la recolección, clasificación y presentación de los hechos sujetos a una apreciación numérica como base a la explicación, descripción y comparación de los fenómenos". (Yale y Kendal, 1954).
Cualquiera sea el punto de vista, lo fundamental es la importancia científica que tiene la estadística, debido al gran campo de aplicación que posee.
Población:
El concepto de población en estadística va más allá de lo que comúnmente se conoce como tal. Una población se precisa como un conjunto finito o infinito de personas u objetos que presentan características comunes.
"Una población es un conjunto de todos los elementos que estamos estudiando, acerca de los cuales intentamos sacar conclusiones". Levin & Rubin (1996).
"Una población es un conjunto de elementos que presentan una característica común". Cadenas (1974).
Ejemplo:
Los miembros del Colegio de Ingenieros del Estado Cojedes.
El tamaño que tiene una población es un factor de suma importancia en el proceso de investigación estadística, y este tamaño vienen dado por el número de elementos que constituyen la población, según el número de elementos la población puede ser finita o infinita. Cuando el número de elementos que integra la población es muy grande, se puede considerar a esta como una población infinita, por ejemplo; el conjunto de todos los números positivos. Una población finita es aquella que está formada por un limitado número de elementos, por ejemplo; el número de estudiante del Núcleo San Carlos de la Universidad Nacional Experimental Simón Rodríguez.
Cuando la población es muy grande, es obvio que la observación de todos los elementos se dificulte en cuanto al trabajo, tiempo y costos necesario para hacerlo. Para solucionar este inconveniente se utiliza una muestra estadística.
Es a menudo imposible o poco práctico observar la totalidad de los individuos, sobre todos si estos son muchos. En lugar de examinar el grupo entero llamado población o universo, se examina una pequeña parte del grupo llamada muestra.
Muestra:
"Se llama muestra a una parte de la población a estudiar que sirve para representarla". Murria R. Spiegel (1991).
"Una muestra es una colección de algunos elementos de la población, pero no de todos". Levin & Rubin (1996).
"Una muestra debe ser definida en base de la población determinada, y las conclusiones que se obtengan de dicha muestra solo podrán referirse a la población en referencia", Cadenas (1974).
Ejemplo;
El estudio realizado a 50 miembros del Colegio de Ingenieros del Estado Cojedes.
El estudio de muestras es más sencillo que el estudio de la población completa; cuesta menos y lleva menos tiempo. Por último se aprobado que el examen de una población entera todavía permite la aceptación de elementos defectuosos, por tanto, en algunos casos, el muestreo puede elevar el nivel de calidad.
Una muestra representativa contiene las características relevantes de la población en las mismas proporciones que están incluidas en tal población.
Los expertos en estadística recogen datos de una muestra. Utilizan esta información para hacer referencias sobre la población que está representada por la muestra. En consecuencia muestra y población son conceptos relativos. Una población es un todo y una muestra es una fracción o segmento de ese todo.
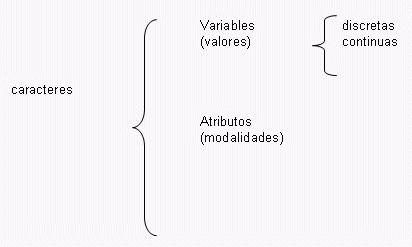
Variables y Atributos:
Las variables, también suelen ser llamados caracteres cuantitativos, son aquellos que pueden ser expresados mediante números. Son caracteres susceptibles de medición. Como por ejemplo, la estatura, el peso, el salario, la edad, etc.
Según, Murray R. Spiegel, (1992) "una variable es un símbolo, tal como X, Y, Hx, que puede tomar un valor cualquiera de un conjunto determinado de ellos, llamado dominio de la variable. Si la variable puede tomar solamente un valor, se llama constante."
Todos los elementos de la población poseen los mismos tipos de caracteres, pero como estos en general no suelen representarse con la misma intensidad, es obvio que las variables toman distintos valores. Por lo tanto estos distintos números o medidas que toman los caracteres son los "valores de la variable". Todos ellos juntos constituyen una variable.
Los atributos también llamados caracteres cualitativos, son aquellos que no son susceptibles de medición, es decir que no se pueden expresar mediante un número.
IUTIN (1997). "Reciben el nombre de variables cualitativas o atributos, aquellas características que pueden presentarse en individuos que constituyen un conjunto.
La forma de expresar los atributos es mediante palabras, por ejemplo; profesión, estado civil, sexo, nacionalidad, etc. Puede notar que los atributos no se presentan en la misma forma en todos los elementos. Estas distintas formas en que se presentan los atributos reciben el nombre de "modalidades".
Ejemplo;
El estado civil de cada uno de los estudiantes del curso de estadísticas I, no se presenta en la misma modalidad en todos.
Estadística Descriptiva:
Tienen por objeto fundamental describir y analizar las características de un conjunto de datos, obteniéndose de esa manera conclusiones sobre las características de dicho conjunto y sobre las relaciones existentes con otras poblaciones, a fin de compararlas. No obstante puede no solo referirse a la observación de todos los elementos de una población (observación exhaustiva) sino también a la descripción de los elementos de una muestra (observación parcial).
En relación a la estadística descriptiva, Ernesto Rivas Gonzáles dice; "Para el estudio de estas muestras, la estadística descriptiva nos provee de todos sus medidas; medidas que cuando quieran ser aplicadas al universo total, no tendrán la misma exactitud que tienen para la muestra, es decir al estimarse para el universo vendrá dada con cierto margen de error; esto significa que el valor de la medida calculada para la muestra, en el oscilará dentro de cierto límite de confianza, que casi siempre es de un 95 a 99% de los casos.
Estadística Inductiva:
Está fundamentada en los resultados obtenidos del análisis de una muestra de población, con el fin de inducir o inferir el comportamiento o característica de la población, de donde procede, por lo que recibe también el nombre de Inferencia estadística.
Según Berenson y Levine; Estadística Inferencial son procedimientos estadísticos que sirven para deducir o inferir algo acerca de un conjunto de datos numéricos (población), seleccionando un grupo menor de ellos (muestra).
El objetivo de la inferencia en investigación científica y tecnológica radica en conocer clases numerosas de objetos, personas o eventos a partir de otras relativamente pequeñas compuestas por los mismos elementos.
En relación a la estadística descriptiva y la inferencial, Levin & Rubin (1996) citan los siguientes ejemplos para ayudar a entender la diferencia entre las dos.
Supóngase que un profesor calcula la calificación promedio de un grupo de historia. Como la estadística describe el desempeño del grupo pero no hace ninguna generalización acerca de los diferentes grupos, podemos decir que el profesor está utilizando estadística descriptiva. Graficas, tablas y diagramas que muestran los datos de manera que sea más fácil su entendimiento son ejemplos de estadística descriptiva.
Supóngase ahora que el profesor de historia decide utilizar el promedio de calificaciones obtenidos por uno de sus grupos para estimar la calificación promedio de las diez unidades del mismo curso de historia. El proceso de estimación de tal promedio sería un problema concerniente a la estadística inferencial.
Los estadísticos se refieren a esta rama como inferencia estadística, esta implica generalizaciones y afirmaciones con respecto a la probabilidad de su validez.
Las variables y su medición:
Una variable es un símbolo, tal como X, Y, H, x ó B, que pueden tomar un conjunto prefijado de valores, llamado dominio de esa variable. Para Murray R. Spiegel (1991) "una variable que puede tomar cualquier valor entre dos valores dados se dice que es una variable continua en caso contrario diremos que la variable es discreta".
Las variables, también llamadas caracteres cuantitativos, son aquellas cuyas variaciones son susceptibles de ser medidas cuantitativamente, es decir, que pueden expresar numéricamente la magnitud de dichas variaciones. Por intuición y por experiencia sabemos que pueden distinguirse dos tipos de variables; las continuas y las discretas
Las variables continuas se caracterizan por el hecho de que para todo para de valores siempre se puede encontrar en valor intermedio, (el peso, la estatura, el tiempo empleado para realizar un trabajo, etc.)
Una variable es continua, cuando puede tomar infinitos valores intermedios dentro de dos valores consecutivos. Por ejemplo, la estatura, el peso, la temperatura.
Ejemplo:
En el preescolar Blanca de Pérez, ubicado en la urbanización Monseñor Padilla de esta ciudad se procedió a recoger las medidas de talla y peso de los niños que a este asisten.
Niño Peso Talla
José 18,300 1,15
Julio 20,500 1,20
Pedro 19,000 1,10
Luis 18,750 1,18
.Las variables discretas serán aquellas que pueden tomar solo un número limitado de valores separados y no continuos; son aquellas que solo toman un determinado números de valores, porque entre dos valores consecutivos no pueden tomar ningún otro; por ejemplo el número de estudiantes de una clase es una variable discreta ya que solo tomará los valores 1, 2, 3, 4... nótese que no encontramos valor como 1,5 estudiantes
Medición de Caracteres
Medición
Existen diversas definiciones del termino "medición", pero estas dependen de los diferentes puntos de vista que se puedan tener al abordar el problema de la cuantificación y el proceso mismo de la construcción de una escala o instrumento de medición.
En general, se entiende por medición la asignación de números a elementos u objetos para representar o cuantificar una propiedad. El problema básico está dado por la asignación un numeral que represente la magnitud de la característica que queremos medir y que dicho números pueden analizarse por manipulaciones de acuerdo a ciertas reglas. Por medio de la medición, los atributos de nuestras percepciones se transforman en entidades conocidas y manejables llamadas "números". Es evidente que el mundo resultaría caótico si no pudiéramos medir nada. En este caso cabría preguntarse de que le serviría la físico saber que el hierro tiene una alta temperatura de fusión.
Niveles o Escalas de mediciones
Escala Nominal:
La escala de medida nominal, puede considerarse la escala de nivel más bajo, y consiste en la asignación, puramente arbitraria de números o símbolos a cada una de las diferentes categorías en las cuales podemos dividir el carácter que observamos, sin que puedan establecerse relaciones entre dichas categorías, a no ser el de que cada elemento pueda pertenecer a una y solo una de estas categorías.
Se trata de agrupar objetos en clases, de modo que todos los que pertenezcan a la misma sean equivalentes respecto del atributo o propiedad en estudio, después de lo cual se asignan nombres a tales clases, y el hecho de que a veces, en lugar de denominaciones, se le atribuyan números, puede ser una de las razones por las cuales se le conoce como "medidas nominales".
Por ejemplo, podemos estar interesados en clasificar los estudiantes de la UNESR Núcleo San Carlos de acuerdos a la carrera que cursan.
| Carrera | Número asignada a la categoría |
| Educación | 1 |
| Administración | 2 |
Se ha de tener presente que los números asignados a cada categoría sirven única y exclusivamente par identificar la categoría y no poseen propiedades cuantitativas.
Escala Ordinal:
En caso de que puedan detectarse diversos grados de un atributo o propiedad de un objeto, la medida ordinal es la indicada, puesto que entonces puede recurrirse a la propiedad de "orden" de los números asignándolo a los objetos en estudio de modo que, si la cifra asignada al objeto A es mayor que la de B, puede inferirse que A posee un mayor grado de atributo que B.
La asignación de números a las distintas categorías no puede ser completamente arbitraria, debe hacerse atendiendo al orden existente entre éstas.
Los caracteres que posee una escala de medida ordinal permiten, por el hecho mismo de poder ordenar todas sus categorías, el cálculo de las medidas estadísticas de posición, como por ejemplo la mediana.
Ejemplo:
Al asignar un número a los pacientes de una consulta médica, según el orden de llegada, estamos llevando una escala ordinal, es decir que al primero en llegar ordinal, es decir que al primeo en llegar le asignamos el nº 1, al siguiente el nº 2 y así sucesivamente, de esta forma, cada número representará una categoría en general, con un solo elemento y se puede establecer relaciones entre ellas, ya que los números asignados guardan la misma relación que el orden de llegada a la consulta.
Escalas de intervalos iguales:
la escala de intervalos iguales, está caracterizada por una unidad de medida común y constante que asigna un número igual al número de unidades equivalentes a la de la magnitud que posea el elemento observado. Es importante destacar que el punto cero en las escalas de intervalos iguales es arbitrario, y no refleja en ningún momento ausencia de la magnitud que estamos midiendo. Esta escala, además de poseer las características de la escala ordinal, encontramos que la asignación de los números a los elemento es tan precisa que podemos determinar la magnitud de los intervalos (distancia) entre todos los elementos de la escala. Sin lugar a dudas, podemos decir que la escala de intervalos es la primera escala verdaderamente cuantitativa y a los caracteres que posean esta escala de medida pueden calculársele todas las medidas estadísticas a excepción del coeficiente de variación.
Ejemplo:
El lapso transcurrido entre 1998-1999 es igual al que transcurrió entre 2000-2001.
Escala de coeficientes o Razones:
El nivel de medida más elevado es el de cocientes o razones, y se diferencia de las escalas de intervalos iguales únicamente por poseer un punto cero propio como origen; es decir que el valor cero de esta escala significa ausencia de la magnitud que estamos midiendo. Si se observa una carencia total de propiedad, se dispone de una unidad de medida para el efecto. A iguales diferencias entre los números asignados corresponden iguales diferencias en el grado de atributo presente en el objeto de estudio. Además, siendo que cero ya no es arbitrario, sino un valor absoluto, podemos decir que A. Tiene dos, tres o cuatro veces la magnitud de la propiedad presente en B.
Ejemplo:
En una encuesta realizada en un barrio de esta localidad se observó que hay familias que no tienen hijos, otras tienen 6 hijos que es exactamente el doble de hijos que aquellas que tienen 3 hijos.
Datos Estadísticos:
Los datos estadísticos no son otra cosa que el producto de las observaciones efectuadas en las personas y objetos en los cuales se produce el fenómeno que queremos estudiar. Dicho en otras palabras, son los antecedentes (en cifras) necesarios para llegar al conocimiento de un hecho o para reducir las consecuencias de este.
Los datos estadísticos se pueden encontrar de forma no ordenada, por lo que es muy difícil en general, obtener conclusiones de los datos presentados de esta manera. Para poder obtener una precisa y rápida información con propósitos de descripción o análisis, estos deben organizarse de una manera sistemática; es decir, se requiere que los datos sean clasificados. Esta clasificación u organización puede muy bien hacerse antes de la recopilación de los datos.
Ejemplo:
Si se quiere conocer las características de los estudiantes del Núcleo San Carlos de la UNESR, que solicitan préstamo a la biblioteca de dicha Universidad, la recolección de la información debe clasificar a cada estudiante sobre la base de: Carrera que estudia, edad, semestre de estudios, etc. Vemos pues que la clasificación marca la pauta de la clase de datos que debe ser obtenido.
Clasificación de los datos
Los datos estadísticos pueden ser clasificados en cualitativos, cuantitativos, cronológicos y geográficos.
Datos Cualitativos: cuando los datos son cuantitativos, la diferencia entre ellos es de clase y no de cantidad.
Ejemplo:
Si deseamos clasificar los estudiantes que cursan la materia de estadística I por su estado civil, observamos que pueden existir solteros, casados, divorciados, viudos.
Datos cuantitativos: cuando los valores de los datos representan diferentes magnitudes, decimos que son datos cuantitativos.
Ejemplo:
Se clasifican los estudiantes del Núcleo San Carlos de la UNESR de acuerdo a sus notas, observamos que los valores (nota) representan diferentes magnitudes.
Datos cronológicos: cuando los valores de los datos varían en diferentes instantes o períodos de tiempo, los datos son reconocidos como cronológicos.
Ejemplo:
Al registrar los promedios de notas de los Alumnos del Núcleo San Carlos de la UNESR en los diferentes semestres.
Datos geográficos: cuando los datos están referidos a una localidad geográfica se dicen que son datos geográficos.
Ejemplo
El número de estudiantes de educación superior en las distintas regiones del país.
Fuentes de datos Estadísticos:
Los datos estadísticos necesarios para la comprensión de los hechos pueden obtenerse a través de fuentes primarias y fuentes secundarias.
Fuentes de datos primarias: es la persona o institución que ha recolectado directamente los datos.
Fuentes secundarias: son las publicaciones y trabajos hechos por personas o entidades que no han recolectado directamente la información.
Las fuentes primarias más confiables, son las efectuadas por oficinas gubernamentales encargadas de tal fin.
En la práctica, es aconsejable utilizar fuentes de datos primarias y en última instancia cuando estas no existan, usar estadísticas de fuentes secundarias. Con este último tipo no debemos pasar por alto que la calidad de las conclusiones estadísticas dependen en grado sumo de la exactitud de los datos que se recaben. De anda serviría usar técnicas estadísticas precisas y refinadas para llegar a conclusiones valederas, si estas técnicas no son aplicadas a datos adecuados o confiables.
Cuando un investigador quiere obtener datos estadísticos relativo a un estudio que desea efectuar, puede elegir entre una fuente primaria o en su defecto, una secundaria. O recopilar los datos por sí mismo. La posibilidad mencionada en último termino podrá deberse bien a la inexistencia de los datos o bien a que esto no se encuentran discriminados en la forma requerida.
Ejemplo:
Si un investigador quiere conocer el número de alumnos repitientes en educación media, clasificados por ciclos, para los últimos diez años, el investigador puede usar una fuente primaria, tal como la memoria y cuenta el Ministerio de Educación cada año.
Método para la recolección de datos:
En estadística se emplean una variedad de métodos distintos para obtener información de los que se desea investigar. Discutiremos aquí los métodos más importantes, incluyendo las ventajas y limitaciones de estos.
La entrevista personal: los datos estadísticos necesarios para una investigación, se reúnen frecuentemente mediante un proceso que consiste en enviar un entrevistador o agente, directamente a la persona investigada. El investigador efectuará a esta persona una serie de preguntas previamente escritas en un cuestionario o boleta, donde anotará las respuestas correspondientes. Este procedimiento que se conoce con el nombre de entrevista personal, permite obtener una información más veraz y completa que la que proporcionan otros métodos, debido a que al tener contacto directo con la persona entrevistada, el entrevistador podrá aclarar cualquier duda que se presente sobre el cuestionario o investigación.
Otra ventaja es la posibilidad que tienen los entrevistadores de adaptar el lenguaje de las preguntas al nivel intelectual de las personas entrevistadas.
Una de las desventajas de este método se debe a que si el entrevistador no obra de buena fé o no tiene un entrenamiento adecuado, puede alterar las respuestas por las personas entrevistadas.
Otra desventaja es su alto costo, ya que resulta bastante oneroso el entrenamiento de los agentes o entrenadores y los supervisores de estos, sobre todo si se trata de una investigación extensa.
Cuestionarios por correo: consiste en enviar por correo el cuestionario acompañado por el instructivo necesario, dando en este no solo las instrucciones pertinentes para cada una de las preguntas, sino también una breve explicación del objeto de la encuesta con el fin de evitar interpretaciones erróneas.
Una de las ventajas es que tienen un costo muy inferior al anterior procedimiento, puesto que no hay que incluir gastos de entrenamiento de personal, el único gasto sería el de franqueo postal.
Dentro de las desventajas de este procedimiento podemos señalar que solo un porcentaje bastante bajo de estos es devuelto, en algunos casos no estamos seguros de que los formularios hayan sido recibidos por sus destinatarios y que hayan sido respondido por ellos mismos. Lo que trae como consecuencia que la información se obtenga con una serie de errores difíciles de precisar por el investigador.
Entrevista por teléfono: como lo indica su nombre, este método consiste en telefonear a la persona a entrevistar y hacerle una serie de preguntas. Este método es bastante simple y económico, ya que el entrenamiento y supervisión de las personas encargadas de efectuar las preguntas es siempre fácil.
Entre las limitaciones que presenta este método podemos señalar el número de preguntas que pueden formularse es relativamente limitado; además las investigaciones efectuadas por este método tienen un carácter selectivo, debido a que muchas de las personas que potencialmente podrían ser investigadas no posee servicio telefónico, por lo que quedan sin la posibilidad de ser entrevistados.
Instrumentos para la recolección de datos:
Cuestionarios:
Cualquiera que sea el método por el que se decida el investigador para recabar información, es necesario elaborar un estudio de preguntas.
Los cuestionarios en general, constan de las siguientes partes:
La identificación del cuestionario: nombre del patrocinante de la encuesta, (oficial o privada), nombre de la encuesta, número del cuestionario, nombre del encuestador, lugar y fecha de la entrevista.
Datos de identificación y de carácter social del encuestado: apellidos, nombres, cédula de identidad, nacionalidad, sexo, edad o fecha de nacimiento, estado civil, grado de instrucción, ocupación actual, ingresos, etc.
Datos propios de la investigación, son los datos que interesa conocer para construir el propósito de la investigación.
Como es natural, estas partes, así como las preguntas, varían de acuerdo a la finalidad de la encuesta. En algunos tipos de investigación, la parte referente a los datos personales es eliminada por no tener ningún tipo de interés para el estudio.
Consideraciones que debemos tomar en cuenta:
-
El cuestionario debe ser conciso; tratar en los posible de que con el menor número de preguntas, se obtenga la mejor información.
-
Claridad de la redacción; evitar preguntas ambiguas o que sugieran respuestas incorrectas, por lo que deben estar formuladas las preguntas de la forma más sencilla.
-
Discreción: un cuestionario hecho a conciencia, no debe tener preguntas indiscretas o curiosas, sobre datos personales que puedan ofender al entrevistado.
-
Facilidad de contestación: se deben evitar, en lo posible, las preguntas de respuestas libres o abiertas y también la formulación de preguntas que requieran cálculos numéricos por parte del entrevistado.
-
Orden de las preguntas: estas deben tener una secuencia y un orden lógico, agruparlas procurando que se relacionen unas con otras.
Series o distribuciones estadísticas:
Anteriormente hemos señalado que la estadística, no se encarga del estudio de un hecho aislado, sino que tienen por objeto de los colectivos. Pues bien cuando se realiza una investigación se obtiene una masa de datos que deben ser organizados para disponerlos en un orden, arreglo o secuencia lógica, con el fin de facilitar el análisis de los mismos esta colección de datos numéricos obtenidos de la observación, que se clasifican y ordenan según un determinado criterio, se denominan "series estadísticas", también conocidas como "distribución estadística".
Clasificación de las series estadísticas:
Series temporales o cronológicas; estas se definen como una masa o conjunto de datos producto de la observación de un fenómeno individual o colectivo, cuantificable en sucesivos instantes o periodos de tiempo.
Ejemplo:
Producción nacional de madera en Rola en m³
Rollizos (periodo 1993 - 1998)
| Años | Producción (m³ rollizos) |
| 1993 | 1.161.061,454 |
| 1994 | 981.668,626 |
| 1995 | 1.087.926,142 |
| 1996 | 1.440.306,250 |
| 1997 | 1.618.075,000 |
| 1998 | 1.027.177,876 |
Fuente: MARN - D.G.S Recurso Forestal. 1999
CVG - PROFORCA
Es importante resaltar que cuando se trata de series temporales o cronológicas, se debe especificar el instante o el periodo de tiempo a los que se refieren los caracteres en estudio.
Cuando nos referimos a instantes de tiempo, por el hecho de que la observación se hace en un momento específico de tiempo.
Ejemplo:
Plantaciones forestales ejecutadas a nivel nacional, al 31 de diciembre de cada año entre 1997 - 2001.
Series atemporales; cuando las observaciones de un fenómeno se hacen referidas al mismo instante o intervalo de tiempo, nos encontramos ente una serie atemporal. Aquí el tiempo no va incluido a cada observación, puesto que es el mismo tiempo para todas ellas. Este tipo de observación proporciona una "visión instantánea" de los fenómenos o caracteres de los componentes del colectivo en estudio.
Ejemplo:
Las notas de las participantes en la materia de estadística I en el periodo académico que terminó en septiembre del 2001.
2.1) series de frecuencia; cuando realizamos un estudio de cada uno de los elementos que componen la población o muestra bajo análisis, observamos que en general, hay un número de veces en que aparece repetido un mismo valor de una variable, o bien repeticiones de la misma modalidad de un atributo. Este número de repeticiones de un resultado, recibe el nombre de frecuencia absoluta o simplemente frecuencia.
El procedimiento mediante el cual se realiza el conteo, para así determinar el número de veces que cada dato se repite, recibe el nombre de tabulación.
Ejemplo:
Consideremos las edades de 20 niños, pertenecientes al Preescolar Blanca de Pérez, ubicado en la urbanización Monseñor Padilla
| 5 | 6 | 5 | 4 | 3 |
| 6 | 3 | 4 | 5 | 4 |
| 3 | 4 | 6 | 5 | 3 |
| 4 | 3 | 6 | 4 | 6 |
Tabulando los datos tenemos
Niños distribuidos por edades:
| Edad (variable) | Nº de niños (Frecuencia) |
| 3 | 5 |
| 4 | 6 |
| 5 | 4 |
| 6 | 5 |
| Total = | 20 |
Al agrupar los resultados de las observaciones en término de las veces que éstos se repiten, da lugar a las llamadas "series de frecuencias" o distribuciones de frecuencias; las cuales se dividen a su vez en series de frecuencia cualitativas y cuantitativas, según que los caracteres de estudio se refieran a atributos o variables respectivamente.
2.2.1) Series de frecuencia acumulativa: son comúnmente llamadas series de frecuencia de atributos o caracteres cualitativos y las formas de representar un atributo recibe el nombre de modalidades.
Cuando se observan y se obtienen los elementos que deseamos estudiar con respecto a un carácter de tipo cualitativo y se procede a agruparlos según las distintas modalidades que toma el atributo, "frecuencia cualitativa".
Ejemplo:
Agrupamos los resultados obtenidos al observar los 35 estudiantes de la materia estadística I, respecto a su estado civil.
Estudiantes de la materia Estadísticas I, clasificados por su estado civil.
| Estado civil | Nº de Estudiantes (frecuencia) |
| Solteros | 18 |
| Casados | 12 |
| Viudos | 1 |
| Divorciados | 4 |
2.1.2) Series de frecuencias cualitativas: es el resultado del agrupamiento de los valores que se repiten (frecuencia) al ser observada una variable.
Ejemplo:
Tomamos nuevamente los 35 estudiantes de la materia estadística I, respecto a su edad.
| Edad (en años) | Nº de estudiantes (frecuencia) |
| 19 | 12 |
| 20 | 2 |
| 25 | 8 |
| 28 | 6 |
| 32 | 4 |
| 42 | 3 |
| Total = | 35 |
2.2) series especiales o geográficas: es aquella que está formada por los valores que toman una variable en función del espacio geográfico.
Documento cedido por:
JORGE L. CASTILLO T.
TRABAJO PRÁCTICO DE MATEMÁTICA
INTRODUCCIÓN A LA ESTADÍSTICA
Concepto de estadística
La estadística es el campo de la matemática que trata de encontrar las leyes que rigen el mundo del azar a fin de tomar las decisiones oportunas en aquellos aspectos de nuestro entorno que parecen estar dominados por lo aleatorio.
Reseña histórica
Desde los comienzos de la civilización han existido formas sencillas de estadística, pues ya se utilizaban representaciones gráficas y otros símbolos en pieles, rocas, palos de madera y paredes de cuevas para contar el número de personas, animales o cosas. Hacia el año 3000 a. C. los babilonios usaban pequeñas tablillas de arcilla para recopilar datos sobre la producción agrícola y sobre los géneros vendidos o cambiados mediante trueque. En el siglo XXXI a. C., mucho antes de construir las pirámides, los egipcios analizaban los datos de la población y la renta del país. Los libros bíblicos de Números y Crónicas incluyen, en algunas partes, trabajos de estadística. El primero contiene dos censos de la población de Israel y el segundo describe el bienestar material de las diversas tribus judías. En China existían registros numéricos similares con anterioridad al año 2000 a. C. Los griegos clásicos realizaban censos cuya información se utilizaba hacia el 594 a. C. para cobrar impuestos. El Imperio romano fue el primer gobierno que recopiló una gran cantidad de datos sobre la población, superficie y renta de todos los territorios bajo su control. Durante la edad media sólo se realizaron algunos censos exhaustivos en Europa. Los reyes caloringios Pipino el Breve y Carlomagno ordenaron hacer estudios minuciosos de las propiedades de la Iglesia en los años 758 y 762 respectivamente. Después de la conquista normanda de Inglaterra en 1066, el rey Guillermo I de Inglaterra encargó la realización de un censo. La información obtenida con este censo, llevado a cabo en 1086, se recoge en el Domesday Book. El registro de nacimientos y defunciones comenzó en Inglaterra a principios del siglo XVI, y en 1662 apareció el primer estudio estadístico notable de población, titulado Observations on the London Bills of Mortality Comentarios sobre las partidas de defunción en Londres. Un estudio similar sobre la tasa de mortalidad en la ciudad de Breslau, en Alemania, realizado en 1691, fue utilizado por el astrónomo inglés Edmund Halley como base para la primera tabla de mortalidad. En el siglo XIX, con la generalización del método científico para estudiar todos los fenómenos de las ciencias naturales y sociales, los investigadores aceptaron la necesidad de reducir la información a valores numéricos para evitar la ambigüedad de las descripciones verbales. En nuestros días, la estadística se ha convertido en un método efectivo para describir con exactitud los valores de datos económicos, políticos, sociales, psicológicos, biológicos o físicos, y sirve como herramienta para relacionar y analizar dichos datos. El trabajo del experto estadístico no consiste ya sólo en reunir y tabular los datos, sino sobre todo en el proceso de “interpretación” de esa información. El desarrollo de la teoría de la probabilidad ha aumentado el alcance de las aplicaciones de la estadística. Muchos conjuntos de datos se pueden aproximar, con gran exactitud, utilizando determinadas distribuciones probabilísticas; los resultados de éstas se pueden utilizar para analizar datos estadísticos. La probabilidad es útil para comprobar la fiabilidad de las inferencias estadísticas y para predecir el tipo y la cantidad de datos necesarios en un determinado estudio estadístico.
Descripción del método estadístico
ð La estadística trata en primer lugar, de acumular la masa de datos numéricos provenientes de la observación de multitud de fenómenos, procesándolos de forma razonable. Mediante la teoría de la probabilidad analiza y explora la estructura matemática subyacente al fenómeno del que estos datos provienen y, trata de sacar conclusiones y predicciones que ayuden al mejor aprovechamiento del fenómeno.
ð La recolección de datos de un fenómeno, una situación particular. Para ver en lo profundo de las cosas hay que aprender a mirar correctamente, no te fíes de unas tablas solo porque contengan muchos números. Tal vez han sido obtenidas observando lo que es totalmente irrelevante para lo que se pretende demostrar.
ð El diseño de experimentos y la teoría de muestras son ahora disciplinas matemáticas profundas que se ocupan de este estadio inicial
ð La tarea de describir y procesar de modo adecuado la masa de datos, provenientes de las observaciones y experimentos, es el objeto de la estadística descriptiva. Se realiza mediante gráficas o bien mediante números o parámetros estadísticos que esquematizan la información
Definición:
Población: el conjunto de todos los individuos cuyo conocimiento es objeto de interés desde un punto de vista estadístico.
Individuo: en estadística, cada uno de los elementos del colectivo (la población) que es objeto de estudio.
Muestra: es un subconjunto limitado extraído de una población con el objeto de reducir el campo de experiencias. Las propiedades que obtengamos se harán extensivas a toda la población.
Carácter o atributo: para el conocimiento de una población estadística, deberemos analizar a cada uno de sus individuos(o a cada individuo de una muestra).Pero ese anali9cis no puede ser exhaustivo; deberemos seleccionar uno o varios detalles (caracteres) y ver cómo se manifiesta ese carácter en cada uno de los individuos. Por ejemplo, de una población de maíz, los caracteres dignos de estudio pueden ser: color, número de granos, longitud, peso, etc.
Los caracteres pueden ser:
Cualitativos: Que se presentan bajo varias cualidades no medibles. Por ejemplo, el color.
Cuantitativos: Es cuando son medibles. Por ejemplo, la longitud de un grano de maíz, su peso, el número de granos total, etc.
Variable estadística: Una variable es una característica (magnitud, vector o número) que puede ser medida y según como se observe, puede variar su valor en diferentes casos como personas, lugares o cosas.
Variable discreta: Un carácter cuantitativo es discreto cuando solo puede tomar determinados valores.
Variable continua: Un carácter cuantitativo es continuo cuando puede tomar valores tan próximos como se quiera. Por ejemplo longitud, peso, etc.
Frecuencia:
Frecuencia absoluta:
La frecuencia absoluta es el número de veces que aparece un valor ( x i ) en los datos obtenidos.
En nuestro ejemplo, la frecuencia absoluta indica el número de familias que tienen esa cantidad de hijos:
TABLA:
| Cantidad de hijos(x i ) | Familias (f i ) |
| 0 | 4 |
| 1 | 9 |
| 2 | 12 |
| 3 | 10 |
| 4 | 8 |
| 5 | 4 |
| 6 | 2 |
| 7 | 1 |
Frecuencia relativa:
La frecuencia relativa es el cociente entre la frecuencia absoluta (f i ) y el número total de datos ( n ).
En nuestro ejemplo, n = 50:
TABLA:
| x i | f i | h i |
| 0 | 4 | 0,08 |
| 1 | 9 | 0,18 |
| 2 | 12 | 0,24 |
| 3 | 10 | 0,20 |
| 4 | 8 | 0,16 |
| 5 | 4 | 0,08 |
| 6 | 2 | 0,04 |
| 7 | 1 | 0,02 |
Acumulada:
En una tabla de frecuencias, cuando la variable es cuantitativa y, por tanto, los distintos valores de la tabla aparecen ordenados de menor a mayor, se llama frecuencia acumulada de un valor de la variable a la suma de su frecuencia con las frecuencias de los valores anteriores.
Tipos de gráficas:
Líneas: En este tipo de gráfico se representan los valores de los datos en dos ejes cartesianos ortogonales entre sí.
Se pueden usar para representar:
-
Una serie
-
Dos o más series
Barras:
Gráficos de barras verticales:
Representan valores usando trazos verticales, aislados o no unos de otros, según la variable a graficar sea discreta o continua. Pueden usarse para representar:
![]()
una serie
![]()
dos o más series (también llamado de barras comparativas)
Gráficos de barras horizontales:
Representan valores discretos a base de trazos horizontales, aislados unos de otros. Se utilizan cuando los textos correspondientes a cada categoría son muy extensos.
![]()
Para una serie
Para dos o más series
Gráficos de barras proporcionales
Se usan cuando lo que se busca es resaltar la representación de los porcentajes de los datos que componen un total.
Las barras pueden ser:
![]()
Verticales
![]()
Horizontales
Gráficos de barras comparativas
Se utilizan para comparar dos o más series, para comparar valores entre categorías.
Las barras pueden ser:
![]()
verticales
![]()
horizontales
Pictogramas:
Los pictogramas son gráficos similares a los gráficos de barras, pero empleando un dibujo en una determinada escala para expresar la unidad de medida de los datos. Generalmente este dibujo debe cortarse para representar los datos.
Es común ver gráficos de barras donde las barras se reemplazan por dibujos a diferentes escalas con el único fin de hacer más vistoso el gráfico, estos tipos de gráficos no constituyen un pictograma.
Pueden ser:
![]()
en dos dimensiones
![]()
en tres dimensiones.
Circular o de sectores:
Estos gráficos nos permiten ver la distribución interna de los datos que representan un hecho, en forma de porcentajes sobre un total. Se suele separar el sector correspondiente al mayor o menor valor, según lo que se desee destacar.
Se pueden ser:
![]()
en dos dimensiones
![]()
en tres dimensiones.
Histograma. Polígono de frecuencias:
Estos tipos de gráficos se utilizan para representa distribuciones de frecuencias. Algunos software específicos para estadística grafican la curva de gauss superpuesta con el histograma.
De tallo y hoja: Una técnica de recuento y ordenación de datos la constituye los diagramas de Tallos y Hojas.
Supongamos la siguiente distribución de frecuencias
36 25 37 24 39 20 36 45 31 31
39 24 29 23 41 40 33 24 34 40
Que representan la edad de un colectivo de N = 20 personas y que vamos a representar mediante un diagrama de Tallos y Hojas. Comenzamos seleccionando los tallos que en nuestro caso son las cifras de decenas, es decir 3, 2, 4, que reordenadas son 2, 3 y 4. A continuación efectuamos un recuento y vamos “añadiendo” cada hoja a su tallo . Por último reordenamos las hojas y hemos terminado el diagrama

Parámetro de posición:
Media aritmética o promedio:
Media aritmética o promedio, de una cantidad finita de números, es igual a la suma de todos ellos dividida entre el número de sumandos.(es un promedio)
Por ejemplo, la media aritmética de 8, 5 y -1 es igual a (8 + 5 + (-1)) / 3 = 4.
Mediana: Es el dato que ocupa el valor central, después de haber sido ordenados éstos. Le corresponde un percentil del 50%. Si n es par, se toma como mediana la media aritmética de los dos valores centrales.
Moda: Es el valor que cuenta con una mayor frecuencia en una distribución de datos. Ejemplo:
En la distribución: 5, 8, 9, 4, 5, 5, 8, 1, 2
La moda es 5, pues es el valor que cuenta con la mayor frecuencia: Aparece 3 veces.
Una distribución puede tener mas de una moda si dos o mas datos, o clases de datos, tienen la misma frecuencia y esta es la mas alta de la distribución.
Parámetros de dispersión:
La varianza: promedia la distancia existente entre los valores de la serie y la media. Se calcula como sumatorio de las diferencias al cuadrado entre cada valor y la media, multiplicadas por el número de veces que se ha repetido cada valor. El sumatorio obtenido se divide por el tamaño de la muestra.
Desviación típica: es la raíz cuadrada de la varianza. Posee las mismas unidades que la media.

Para estimar la desviación típica de una población a partir de los datos de una muestra se utiliza la fórmula (cuasi desviación típica):
Rango: mide la amplitud de los valores de la muestra y se calcula por diferencia entre el valor más elevado y el valor más bajo.
Rango = Dato Mayor - Dato Menor.
Corresponde a un gráfico de barras vistoso o elegante, donde se reemplazó la barra vertical por un dibujo alusivo al tema del gráfico.
Descargar
| Enviado por: | Wilfredo8 |
| Idioma: | castellano |
| País: | Venezuela |
