Estadística
Estadística
INTRODUCCIÓN
La estadística se aplica prácticamente en todos los campos del saber humano.
La estadística es el estudio científico de datos numéricos basados en fenómenos naturales. Es una técnica matemática de investigación que ayuda a delimitar una muestra, a reconocer los datos, ordenarlos, presentarlos, analizarlos y sacar conclusiones.
La estadística es una rama de las matemáticas que estudia los métodos de obtención de datos sobre una población analizándolos con el fin de hallar alguna información para un efecto dado.
La estadística generalmente es definida como la rama de las matemáticas que se ocupa de reunir, organizar y analizar datos numéricos y así mismo que ayuda a resolver problemas como el diseño de experimentos y la toma de decisiones.
La estadística inferencial trabaja con muestras, subconjuntos, formados por algunos individuos de la población. A partir del estudio de la muestra se pretende inferir aspectos relevantes de toda la población.
La estadística descriptiva analiza, estudia y describe a la totalidad de individuos de una población. Su finalidad es obtener información, analizarla, elaborarla y simplificarla lo necesario para que pueda ser interpretada cómoda y rápidamente.
OBJETIVOS
GENERAL
Por medio de este trabajo se pretende dar a conocer la gran importancia de la estadística, y su aplicación en la vida cotidiana, al igual que se pretende dar a conocer los distintos términos que son utilizados para realizar un estudio estadístico y las diferentes clases de graficas que hay para poder representar los datos estadísticos.
ESPECÍFICOS
-
Informarse sobre la estadística.
-
Identificar los distintos términos estadísticos.
-
Reconocer las diferentes clases de diagramas estadísticos.
-
Distinguir las diferentes clasificaciones de datos estadísticos.
-
Conocer sobre la tabulación de las encuestas.
-
Diferenciar las medidas de tendencia central para datos no agrupados
-
Señalar las medidas de tendencia central de los datos agrupados.
-
Determinar las medidas de dispersión para datos no agrupados y para datos agrupados.
-
Diversificar los términos de media, moda y mediana
-
Enumerar las medidas de dispersión.
-
Indagar acerca de la distribución normal.
ESTADÍSTICA
Rama de las matemáticas que se ocupa de reunir, organizar y analizar datos numéricos y que ayuda a resolver problemas como el diseño de experimentos y la toma de decisiones.
A la estadística se le considera frecuentemente como una colección de hechos numéricos expresados en términos, de proposiciones concisas y que han sido recopilados mediante varias observaciones, o a partir de otros datos numéricos.
La ESTADISTICA es la ciencia que le facilita al hombre el estudio de datos masivos, pasa de esa manera sacar conclusiones valederas y efectuar predicciones razonables de ellos; y así mostrar una visión de conjunto clara y de más fácil apreciación, así como para describirlos y compararlos.
En una forma práctica, la ESTADÍSTICA nos proporciona los métodos científicos para la recopilación, organización, resumen, representación y ANALISIS de DATOS, o análisis de hechos, que se presenten a una valuación numérica; tales como son: Características biológicas o sociológicas, fenómenos físicos, producción, calidad, población riqueza, impuestos, cosechas, etc.
La cualidad de CIENCIA de la Estadística se presta aún a polémica; pero es un hecho indiscutible el que viene a constituir un auxiliar maravilloso y sobretodo insustituible para la investigación científica, al permitir que se aproveche el material cuantitativo que arrojan las observaciones y los experimentos.
Sólo mediante el empleo de los procederes estadísticos se hace posible el ordenamiento, clasificación, presentación y estudio claro de datos, hechos y ocurrencias masivas; los cuales de ordinario presentan una apariencia confusa, cambiante, afectados por interrelaciones diversas y variaciones sin regulaciones aparentes; que de otra forma no se podrían apreciar.
Desde esta perspectiva, la estadística constituye una colección de proposiciones tales como:
-
El coeficiente intelectual (CI) medio de los niños de 5º de primaria es…
-
Siete de cada diez personas prefieren la marca X a la marca Y.
-
Los campeones mundiales de fútbol marcaron 15 goles en su última gira.
La estadística puede ser considerada también como un método para manejar los datos. Esta definición destaca el punto de vista de que la distancia es una herramienta para la recopilación, organización y análisis de hechos numéricos o de observaciones.
Sólo cuando nos adentramos en un mundo más específico como es el campo de la investigación de las Ciencias Sociales: Medicina, Biología, Psicología, ... empezamos a percibir que la Estadística no sólo es algo más, sino que se convierte en la única herramienta que, hoy por hoy, permite dar luz y obtener resultados, y por tanto beneficios, en cualquier tipo de estudio, cuyos movimientos y relaciones, por su variabilidad intrínseca, no puedan ser abordadas desde la perspectiva de las leyes deterministas. Podríamos, desde un punto de vista más amplio, definir la estadística como la ciencia que estudia cómo debe emplearse la información y cómo dar una guía de acción en situaciones prácticas que entrañan incertidumbre.
HISTORIA DE LA ESTADÍSTICA
Desde los comienzos de la civilización han existido formas sencillas de estadística, pues ya se utilizaban representaciones gráficas y otros símbolos en pieles, rocas, palos de madera y paredes de cuevas para contar el número de personas, animales o cosas. Hacia el año 3000 a.C. los babilonios usaban pequeñas tablillas de arcilla para recopilar datos sobre la producción agrícola y sobre los géneros vendidos o cambiados mediante trueque. En el siglo XXXI a.C., mucho antes de construir las pirámides, los egipcios analizaban los datos de la población y la renta del país. Los libros bíblicos de Números y Crónicas incluyen, en algunas partes, trabajos de estadística. El primero contiene dos censos de la población de Israel y el segundo describe el bienestar material de las diversas tribus judías. En China existían registros numéricos similares con anterioridad al año 2000 a.C. Los griegos clásicos realizaban censos cuya información se utilizaba hacia el 594 a.C. para cobrar impuestos.
Desde 3.000 años antes de Cristo, se tienen noticias de los primeros censos hechos a la población, en la antigua Babilonia, Persia, Egipto y China, se elaboraban censos de las propiedades de los habitantes con fines impositivos.
El mismo Moisés, que existió en los siglos XV - XIV antes de Cristo, y que era profeta y legislador hebreo, levantó un censo de su pueblo en el desierto, según lo señala la Biblia.
Y en Grecia, el censo era algo muy usual en sus principales ciudades democráticas.
También Servio Tulio, que se supone vivió entre 578 y 534 antes de Cristo, y fue el sexto Rey de Roma, ordenó que se llevara a acabo un censo cada 5 años, y el fin era el de planificar los impuestos, preparar elecciones y la conscripción militar. Como ha de recordarse, San José y la Virgen María iban a Belén a inscribirse en el segundo de estos censos, cuando nació Jesús, según sus discípulos Lucas, y Mateo, ya en la época del Emperador Augusto.
El primer censo en América fue llevado a cabo por los Incas, y lo más probable es que haya sido en la época de Pachacútec Yupanqui, Inca que fue llamado “El Reformador del Mundo” quien organizó el Imperio Incaico económica y socialmente.
El Imperio romano fue el primer gobierno que recopiló una gran cantidad de datos sobre la población, superficie y renta de todos los territorios bajo su control. Durante la edad media sólo se realizaron algunos censos exhaustivos en Europa. Los reyes caloringios Pipino el Breve y Carlomagno ordenaron hacer estudios minuciosos de las propiedades de la Iglesia en los años 758 y 762 respectivamente. Después de la conquista normanda de Inglaterra en 1066, el rey Guillermo I de Inglaterra encargó la realización de un censo. La información obtenida con este censo, llevado a cabo en 1086, se recoge en el Domesday Book. El registro de nacimientos y defunciones comenzó en Inglaterra a principios del siglo XVI, y en 1662 apareció el primer estudio estadístico notable de población, titulado Observations on the London Bills of Mortality (Comentarios sobre las partidas de defunción en Londres). Un estudio similar sobre la tasa de mortalidad en la ciudad de Breslau, en Alemania, realizado en 1691, fue utilizado por el astrónomo inglés Edmund Halley como base para la primera tabla de mortalidad. En el siglo XIX, con la generalización del método científico para estudiar todos los fenómenos de las ciencias naturales y sociales, los investigadores aceptaron la necesidad de reducir la información a valores numéricos para evitar la ambigüedad de las descripciones verbales.
En sus comienzos, la Estadística sólo era aplicada al estudio y valuación numérica de manifestaciones inherentes al ESTADO: De allí sale nombre, del vocablo latino “status”, que fue utilizado por primera vez en Alemania, en el siglo XVII específicamente.
El matemático y filósofo italiano Girolano Cardano, que vivió entre los años 1510 y 1576, realizó los primeros estudios sobre probabilidades, y fueron publicados en su trabajo “Iber de Ludo Alea” que quiere decir “Manual para tirar los dados”.
Felipe II (1575 - 1578) fue el Rey de España, e hizo levantar un censo en el Nuevo Mundo de sus dominios, en el año de 1576.
Gottfried Achenwall (Desde 1719 hasta 1772), un reconocido economista y profesor universitario, de origen alemán, profundizó en estudios que dieron origen a la Estadística Inductiva.
Juan Pedro Sussmilchi, que vivió desde 1707 hasta 1767, y fue un brillante matemático, estadístico y teólogo alemán, perfeccionó los estudios demográficos, al mismo tiempo que Antonio Deparcioux, que vivió entre 1703 y 1768 y fue un gran matemático francés, aplicó la Estadística para obtener las primeras “Tablas de Mortalidad”, con lo cual se dio inicio el próspero negocio del seguro de vida.
Jacques Bernouilli (1654-1705) matemático suizo, escribió “Ars Cojetandi” que quiere decir en español, el Arte de Conjeturar, publicado póstumamente en 1713 y formula la Ley de los Grandes Números, primer paso hacia la Estadística Matemática.
El Marqués Pedro Simón de Laplace que vivió desde 1749 hasta 1827, matemático y astrónomo francés, anuncia su Teoría Analítica de las Probabilidades en 1812, y este fue otro gran impulso a la Estadística Matemática.
Lambert Jacques Quetelet (1796-1874), gran astrónomo y matemático de origen belga, aplicó el método estadístico al estudio de la Economía Social (Características físicas, intelectuales y morales de los humanos); creando así la Sociometría.
Pafnuti Lvovich Chevyshev (1821-1884) crea la Desigualdad de Chevyshev, que es de gran utilidad como herramienta teórica, aplicable a las distribuciones de medias y varianzas finitas.
Gregor Johann Mendel, (1822-1884), conocido botánico austríaco, que experimentó con 34 variedades de arvejas, durante un lapso de 2 años, descubre y enuncia, en el año de 1865, las Leyes de Mendel; leyes estadísticas que rigen la herencia y la hibridación de los vegetales, lo cual es considerado el punto de partida de la biometría.
El científico inglés, Francis Galton (1822-1911), primo de Darwin y creador de la Eugenesia, de nuevos métodos antropométricos, de la moderna teoría de la Estadística y su aplicación a la Sociometría y a la Biometría. Ideó los deciles y centiles.
Karl Pearson (1857-1936), matemático inglés, crea el método de los momentos, la Prueba de chi cuadrana, los conceptos de Curva normal, y de Desviación normal. Publica sus trabajos bajo el epígrafe de Contribución a la teoría matemática de la evolución, y en total, da un gran impulso a las técnicas usadas en estudios de fenómenos sociales (Sociometría) y biológicos (Biometría).
Hoy en día la Estadística ha llegado a tal grado de perfeccionamiento y especialización, que casi no existe disciplina científica, o técnica, de investigación, control o planificación, en la cual no se apliquen los métodos estadísticos como una herramienta de trabajo valiosísima e insustituible.
En nuestros días, la estadística se ha convertido en un método efectivo para describir con exactitud los valores de datos económicos, políticos, sociales, psicológicos, biológicos o físicos, y sirve como herramienta para relacionar y analizar dichos datos. El trabajo del experto estadístico no consiste ya sólo en reunir y tabular los datos, sino sobre todo en el proceso de “interpretación” de esa información. El desarrollo de la teoría de la probabilidad ha aumentado el alcance de las aplicaciones de la estadística. Muchos conjuntos de datos se pueden aproximar, con gran exactitud, utilizando determinadas distribuciones probabilísticas; los resultados de éstas se pueden utilizar para analizar datos estadísticos. La probabilidad es útil para comprobar la fiabilidad de las inferencias estadísticas y para predecir el tipo y la cantidad de datos necesarios en un determinado estudio estadístico.
MÉTODOS ESTADÍSTICOS
La materia prima de la estadística consiste en conjuntos de números obtenidos al contar o medir elementos. Al recopilar datos estadísticos se ha de tener especial cuidado para garantizar que la información sea completa y correcta.
El primer problema para los estadísticos reside en determinar qué información y en que cantidad se ha de reunir. En realidad, la dificultad al compilar un censo está en obtener el número de habitantes de forma completa y exacta; de la misma manera que un físico que quiere contar el número de colisiones por segundo entre las moléculas de un gas debe empezar determinando con precisión la naturaleza de los objetos a contar. Los estadísticos se enfrentan a un complejo problema cuando, por ejemplo, toman una muestra para un sondeo de opinión o una encuesta electoral. El seleccionar una muestra capaz de representar con exactitud las preferencias del total de la población no es tarea fácil.
Para establecer una ley física, biológica o social, el estadístico debe comenzar con un conjunto de datos y modificarlo basándose en la experiencia. Por ejemplo, en los primeros estudios sobre crecimiento de la población, los cambios en el número de habitantes se predecían calculando la diferencia entre el número de nacimientos y el de fallecimientos en un determinado lapso. Los expertos en estudios de población comprobaron que la tasa de crecimiento depende sólo del número de nacimientos, sin que el número de defunciones tenga importancia. Por tanto, el futuro crecimiento de la población se empezó a calcular basándose en el número anual de nacimientos por cada 1.000 habitantes. Sin embargo, pronto se dieron cuenta que las predicciones obtenidas utilizando este método no daban resultados correctos. Los estadísticos comprobaron que hay otros factores que limitan el crecimiento de la población. Dado que el número de posibles nacimientos depende del número de mujeres, y no del total de la población, y dado que las mujeres sólo tienen hijos durante parte de su vida, el dato más importante que se ha de utilizar para predecir la población es el número de niños nacidos vivos por cada 1.000 mujeres en edad de procrear. El valor obtenido utilizando este dato mejora al combinarlo con el dato del porcentaje de mujeres sin descendencia. Por tanto, la diferencia entre nacimientos y fallecimientos sólo es útil para indicar el crecimiento de población en un determinado periodo de tiempo del pasado, el número de nacimientos por cada 1.000 habitantes sólo expresa la tasa de crecimiento en el mismo periodo, y sólo el número de nacimientos por cada 1.000 mujeres en edad de procrear sirve para predecir el número de habitantes en el futuro.
ESTADÍSTICA DESCRIPTIVA
Analiza metódicamente los datos, simplificándolos y presentándolos en forma clara; eliminando la confusión característica de los datos preliminares. Permite la elaboración de cuadros, gráficos e índices bien calculados; suficientemente claros, como para disipar las dudas y la oscuridad de los datos masivos.
Se limita a describir los datos que se analizan, sin hacer inferencias en cuanto a datos no incluidos en la muestra.
La estadística descriptiva analiza, estudia y describe a la totalidad de individuos de una población. Su finalidad es obtener información, analizarla, elaborarla y simplificarla lo necesario para que pueda ser interpretada cómoda y rápidamente y, por tanto, pueda utilizarse eficazmente para el fin que se desee. El proceso que sigue la estadística descriptiva para el estudio de una cierta población consta de los siguientes pasos:
-
Selección de caracteres dignos de ser estudiados.
-
Mediante encuesta o medición, obtención del valor de cada individuo en los caracteres seleccionados.
-
Elaboración de tablas de frecuencias, mediante la adecuada clasificación de los individuos dentro de cada carácter.
-
Representación gráfica de los resultados (elaboración de gráficas estadísticas).
-
Obtención de parámetros estadísticos, números que sintetizan los aspectos más relevantes de una distribución estadística.
ESTADÍSTICA INFERENCIAL
La estadística descriptiva trabaja con todos los individuos de la población. La estadística inferencial, sin embargo, trabaja con muestras, subconjuntos formados por algunos individuos de la población. A partir del estudio de la muestra se pretende inferir aspectos relevantes de toda la población. Cómo se selecciona la muestra, cómo se realiza la inferencia, y qué grado de confianza se puede tener en ella son aspectos fundamentales de la estadística inferencial, para cuyo estudio se requiere un alto nivel de conocimientos de estadística, probabilidad y matemáticas.
La estadística inferencial Provee conclusiones o inferencias, basándose en los datos simplificados y analizados; detectando las interrelaciones que pueden unirlos, las leyes que los rigen y eliminando las influencias del azar; llegando más allá de las verificaciones físicas posibles. Sobre la base de la muestra estudiada saca conclusiones, o sea, hace inferencia o inducción, en cuanto al universo o población, de donde se obtuvo dicha muestra.
Cuando hay problemas cuya resolución se nos torna:
-
Imposible debido a lo inmenso del problema (millones de individuos).
-
Posible, pero ruinoso.
Recurrimos a la estadística inferencial (diseño de experimentos, teoría de muestras, teoría de la estimación, etc.) para hallar respuesta de los interrogantes.
Los datos recogidos deben ser organizados, tabulados y presentados para que su análisis e interpretación sean rápidos y útiles. Por ejemplo, para estudiar e interpretar la distribución de las notas o calificaciones de un examen en una clase con 30 alumnos, primero se ordenan las notas en orden creciente: 3,0; 3,5; 4,3; 5,2; 6,1; 6,5; 6,5; 6,5; 6,8; 7,0; 7,2; 7,2; 7,3; 7,5; 7,5; 7,6; 7,7; 7,8; 7,8; 8,0; 8,3; 8,5; 8,8; 8,8; 9,0; 9,1; 9,6; 9,7; 10 y 10. Esta secuencia muestra, a primera vista, que la máxima nota es un 10, y la mínima es un 3; el rango, diferencia entre la máxima y la mínima es 7.
ESTADÍSTICA METODOLOGICA
La finalidad de esta asignatura es el estudio de los métodos estadísticos en general, aplicables a las investigaciones, como valiosa herramienta auxiliar de la ciencia y de la técnica. Nos señala la forma de proceder en cada caso, los recursos disponibles y aplicables, de acuerdo al objetivo perseguido y al caso particular en estudio.
TÉRMINOS ESTADÍSTICOS
El primer campo de actuación de la estadística, como se ha visto, es la demografía. De esta ciencia ha tomado la nomenclatura (población, individuo…).
Los datos se basan en observaciones individuales o ítems. Así, por ejemplo si se pesan 100 ratones blancos, el peso de cada ratón es una observación individual y los pesos de los 100 ratones representan la muestra de observaciones.
Se llama población al conjunto de todos los elementos cuyo conocimiento interesa. Cada uno de esos elementos es un individuo. Si se está estudiando el resultado de ciertos experimentos químicos, cada uno de esos experimentos será un individuo estadístico y el conjunto de todos los posibles experimentos en esas condiciones será la población.
Cada individuo puede ser descrito mediante uno o varios caracteres. Por ejemplo, si los individuos son personas, el sexo, el estado civil, el número de hermanos o su estatura son caracteres. Y si el individuo es una reacción química, el tiempo de reacción, la cantidad de producto obtenido o si éste es ácido o básico serán posibles caracteres que pueden analizarse.
Un carácter puede ser cuantitativo si es medible numéricamente o cualitativo si no admite medición numérica. El número de hermanos y la estatura son caracteres cuantitativos mientras que el sexo y el estado civil son caracteres cualitativos.
Los distintos valores que puede tomar un carácter cuantitativo configuran una variable estadística. La variable estatura, en cierta población estadística, toma valores en el intervalo 147-205; y la variable número de hermanos toma los valores 0, 1, 2, 3, 4, 5, 6, 7 y 8. Una variable estadística como esta última es discreta, ya que sólo admite valores aislados. Una variable estadística es continua si admite todos los valores de un intervalo, como ocurre con la estatura.
INDIVIDUO
Cada uno de los elementos del colectivo que es objeto de estudio. Por ejemplo, si se están estudiando datos sobre la habitabilidad de las viviendas de una barriada, cada vivienda es un individuo estadístico.
POBLACIÓN
Es la recolección completa de todas las observaciones de interés para el observador.
Es un conjunto completo de individuos, objetos o medidas que tienen una característica común observable.
La población, o el universo, está formado por la totalidad de los elementos que se desean estudiar, ejemplos podrían ser: La población total de Venezuela, los alumnos cursantes en las universidades del país, la producción de toda una industria, a cosecha de un año dado, el rendimiento de una raza de ganado, entre otros.
Por ejemplo: si se esta estudiando el resultado de ciertos experimentos químicos cada uno de esos experimentos será un individuo estadístico y el conjunto de todos los posibles experimentos en esas condiciones será la población.
La población es el conjunto de todos los individuos cuyo conocimiento es objeto de interés desde un punto de vista estadístico. Por ejemplo, si se está interesado en las ventas de los comercios de una cierta ciudad, cada comercio es un individuo, y la población —también llamada universo— es el conjunto de todos los comercios de la ciudad.
El estudio estadístico de una población se puede realizar mediante un análisis exhaustivo de todos sus individuos (estadística descriptiva) o bien mediante una inferencia realizada a partir de una muestra extraída de la población (estadística inferencial).
Una población la constituyen todos los individuos de una especie determinada que se encuentran en un área limitada en un momento dado. La población es la totalidad de observaciones individuales sobre las cuales se hacen inferencias, las cuales existen en cualquier parte del mundo o al menos dentro de un área de muestreo claramente especificada, limitada en espacio y tiempo.
MUESTRA
Conjunto de individuos extraído de una población con el fin de inferir mediante su estudio, características de toda la población.
En los estudios estadísticos, en vez de analizar la totalidad de la población o universo, se acude al recurso de considerar solamente una parte de ella, a la cual se llama muestra.
Es requisito indispensable que la muestra a analizarse sea representativa realmente de la población o universo, al cual substituye en el estudio estadístico, o sea, que debe contener valores típicos del fenómeno que se desea estudiar.
Es un subconjunto de la población o el universo.
Es una parte representativa d la población seleccionada para ser estudiada ya que la población es demasiado grande como para analizarla en su totalidad.
Conjunto de individuos extraídos de una población con el fin de inferir, mediante su estudio, características de toda la población.
Se dice que una muestra es representativa cuando, por la forma en que ha sido seleccionada, aporta garantías suficientes para realizar inferencias fiables a partir de ella.
Una muestra se puede definir como un conjunto de observaciones individuales seleccionadas por un procedimiento específico. Ejemplo, el peso de un ratón a través de un periodo de tiempo.
El diseño de muestra o diseña de encuesta especifica el método de obtención de la muestra.
El diseño no especifica la forma de recolectar o medir los datos reales. Especifica únicamente el método de recolección de los objetos que contienen la información requerida. Estos objetos se llaman elementos.
Un elemento es un objeto del cual se toma una medición.
Los elementos pueden ocurrir individualmente o en grupos en la población. Un grupo de elementos, como una familia o una caja de cerillos se llama unidad de muestreo.
Las unidades de muestreo son colecciones disjuntas de elementos de la población. En algunos casos una unidad muestral esta constituida por un solo elemento.
Para seleccionar una muestra aleatoria de unidades de elementos muéstrales, es necesaria una lista de todas las unidades muéstrales contenidas en la población. Esta lista se le denomina marco muestral.
Un marco muestral es una lista de unidades muéstrales.
MUESTRA ALEATORIA
Es un subconjunto de la población o universo seleccionado en forma tal que cada miembro de la población tenga igual oportunidad de ser elegido.
Muestra elegida independientemente de todas las demás, con la misma probabilidad que cualquier otra y cuyos elementos están elegidos independientemente unos de otros y con la misma probabilidad.
Al seleccionar una muestra aleatoria de n mediciones de una población infinita de N mediciones, si el muestreo se lleva a cabo de forma que todas las muestras posibles de tamaño n tenga la misma probabilidad de ser seleccionadas, el muestreo se llama aleatorio y el resultado es una muestra aleatoria simple.
Una muestra aleatoria estratificada es una muestra aleatoria que se obtiene separando los elementos de la población en grupos disjuntos, llamados estratos, y seleccionando una muestra aleatoria simple dentro de cada estrato.
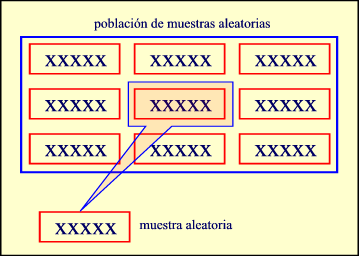
MUESTREO
Proceso por el cual se seleccionan los individuos que formarán una muestra.
Para que se puedan obtener conclusiones fiables para la población a partir de la muestra, es importante tanto su tamaño como el modo en que han sido seleccionados los individuos que la componen.
El tamaño de la muestra depende de la precisión que se quiera conseguir en la estimación que se realice a partir de ella. Para su determinación se requieren técnicas estadísticas superiores, pero resulta sorprendente cómo, con muestras notablemente pequeñas, se pueden conseguir resultados suficientemente precisos. Por ejemplo, con muestras de unos pocos miles de personas se pueden estimar con muchísima precisión los resultados de unas votaciones en las que participarán decenas de millones de votantes.
Para seleccionar los individuos de la muestra es fundamental proceder aleatoriamente, es decir, decidir al azar qué individuos de entre toda la población forma parte de la muestra.
Si se procede como si de un sorteo se tratara, eligiendo directamente de la población sin ningún otro condicionante, el muestreo se llama aleatorio simple o irrestrictamente aleatorio.
Cuando la población se puede subdividir en clases (estratos) con características especiales, se puede muestrear de modo que el número de individuos de cada estrato en la muestra mantenga la proporción que existía en la población. Una vez fijado el número que corresponde a cada estrato, los individuos se designan aleatoriamente. Este tipo de muestreo se denomina aleatorio estratificado con asignación proporcional.
Las inferencias realizadas mediante muestras seleccionadas aleatoriamente están sujetas a errores, llamados errores de muestreo, que están controlados. Si la muestra está mal elegida —no es significativa— se producen errores sistemáticos no controlados.
DATOS
Números o medidas obtenidos como resultado de observaciones. Pueden ser recuentos de frecuencias (datos de frecuencias) tales como el número de personas que manifiestan su preferencia por el candidato liberal; o pueden ser calificaciones, como las que se obtienen en las pruebas psicológicas o de exámenes. A los datos de frecuencias se les llama también datos enumerativos o categóricos.
Los datos Son cada uno de los términos que componen la muestra y, de acuerdo a la función existente entre ellos, también pueden ser discretos o continuos. En general, los discretos son los que pueden contar y los continuos, los que se pueden medir.
VARIABLE
Cualquier característica de una persona, medio ambiente o situación experimental que pueda variar de persona a persona, de un medio ambiente a otro o de una situación experimental a otra. Así el peso, el CI y el sexo son variables, ya que toman valores diferentes al observar distintos individuos.
Es una característica de la población que se esta analizando en un estudio estadístico.
Una variable es una propiedad con respecto a la cual los individuos de una muestra difieren de algún modo verificable. Ejemplo: la longitud, el peso, la altura.
Las variables se dividen en:
-
VARIABLES MEDIBLES: son todas aquellas cuyos diferentes valores pueden expresarse en forma numérica ordenada, pueden ser de dos clases: variables continuas o variables discontinuas.
-
VARIABLES CONTINUAS: pueden tomar un número infinito de valores entre dos puntos determinados, como por ejemplo, las longitudes, áreas, volúmenes, pesos, ángulos, temperaturas, períodos de tiempo, porcentajes y velocidades.
-
VARIABLES DISCONTINUAS: o discretas o mirísticas, solo tienen valores numéricos fijos (enteros) sin posibles valores intermedios. Son ejemplos el número de crías, el número de plantas en un cuadrado determinado.
-
VARIABLES CLASIFICABLES: no pueden medirse pero pueden ordenarse o alinearse por su magnitud.
-
ATRIBUTOS: no pueden medirse sino que deben expresarse cualitativamente. Todas ellas son propiedades tales como: negro o blanco, muerto o vivo, macho o hembra.
PARÁMETRO
Es una medida descriptiva de la población total de todas las observaciones de interés para el observador.
Las tablas estadísticas son una forma organizada de dar toda (o casi toda) la información, todos los datos de que disponemos.
Con las gráficas estadísticas se pierde algo de información (mucho o poco, según los casos).
En cualquiera de los dos casos, la cantidad de datos que se dan es excesiva para que sea operativo, para poder hacer referencias concisas a esa distribución o comparaciones rápidas con otras distribuciones.
Esa es la razón de ser de los parámetros estadísticos, el resumir en un número un aspecto relevante de la distribución que pueda dar una idea de la misma o compararla en ese aspecto con otras.
Cualquier característica medible de una población; por ejemplo: la proporción real de demócratas inscritos entre todos los ciudadanos norteamericanos de edad para votar.
Nos referimos a estas funciones, tales como las medias, desviaciones típicas, momentos, coeficientes de correlación, etc., con el nombre genérico de parámetros. Modernamente se reserva esta palabra para los valores de la población y para designar el valor correspondiente de la muestra se utiliza la palabra estadígrafo. Por lo tanto, una media muestral es un estadígrafo que estima la media de la población, que es un parámetro.
Son cantidades, las cuales son constantes para distribuciones en particular, pero pueden tomar diferentes valores para diferentes miembros de familias de distribuciones del mismo tipo. Los parámetros más comunes son 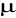
y 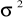
.
Número que se obtiene a partir de los datos de una distribución estadística y que sirve para sintetizar alguna característica relevante de la misma. Conociendo los valores de algunos parámetros, aunque se desconozcan los datos de la distribución, se adquiere una idea suficientemente clara de ella.
Los parámetros estadísticos correspondientes a distribuciones con una variable se pueden clasificar del siguiente modo: medidas de centralización, medidas de dispersión y medidas de posición.
Las medidas de centralización son parámetros estadísticos alrededor de los cuales se distribuyen los datos de la distribución y se toman como el centro de la misma. Las más importantes son la media, la mediana y la moda.
Las medidas de dispersión son parámetros estadísticos que indican cuánto se alejan del centro los valores de la distribución. Las más importantes son la desviación típica y la varianza.
Las medidas de posición sirven para indicar la proporción de individuos de la distribución que hay antes y después de un determinado valor. Las más importantes son los cuartiles y los percentiles o centiles.
Ciertos parámetros estadísticos indican si la distribución es más o menos asimétrica (coeficiente de asimetría) y más o menos picuda o aplastada (coeficiente de aplastamiento).
Existen también parámetros estadísticos correspondientes a distribuciones bidimensionales (con dos variables), que sirven para indicar la relación entre las variables: la covarianza, el coeficiente de correlación y el coeficiente de regresión.
ERROR DE MUESTREO
Es la diferencia entre el parámetro desconocido de la población y el estadístico de la muestra utilizado para calcular el parámetro.
Las inferencias realizadas mediante muestras seleccionadas aleatoriamente están sujetas a errores, llamados errores de muestreo, que están controlados. Si la muestra está mal elegida —no es significativa— se producen errores sistemáticos no controlados.
Sea el estimador muestral del parámetro poblacional. El error de estimación es la diferencia absoluta ø- ø.
SESGO MUESTRAL
Es la tendencia a favorecer la selección de ciertos elementos de la muestra en lugar de otros.
Los sesgos son precisamente el principal problema a controlar en la realización de una encuesta; pueden provenir de errores muestrales, que dan como resultado una mayor presencia de un grupo de individuos con determinadas características, y/o de la mayor o menor accesibilidad a la entrevista de determinados grupos de personas. También se pueden producir por errores en el cuestionario, que o bien inducen determinadas respuestas, o no tienen en cuenta todas las opciones posibles de los entrevistados. Y, finalmente, pueden aparecer sesgos en el tratamiento estadístico, al establecer las variables a utilizar y al agrupar los datos o los individuos en determinadas categorías.
Las curvas que representan los puntos de datos de un conjunto de datos pueden ser simétricas o sesgadas. Las curvas simétricas, tienen una forma tal que una línea vertical que pase por el punto más alto de la curva dividirá el área de ésta en dos partes iguales. Cada parte es una imagen espejo de la otra. En las curvas sesgadas, los valores de su distribución de frecuencias están concentrados en el extremo inferior o en el superior de la escala de medición del eje horizontal. Los valores no están igualmente distribuidos. Las curvas pueden estar sesgadas hacia la derecha (positivamente sesgadas) o sesgadas hacia la izquierda (negativamente sesgadas).
MARCA DE CLASES
Se le llama marca de clase a los valores representativos de todos los valores incluidos en el intervalo respectivo; equivale a la semisuma de los límites inferior y superior de un intervalo.
Es el valor medio de los límites de cada intervalo de clase. Suelen escogerse siempre intervalos de extensiones iguales.
ETAPAS PARA REALIZAR UN ESTUDIO ESTADÍSTICO…
-
Selección de caracteres dignos de ser estudiados.
-
Mediante encuestas o medición, obtención del valor de cada individuo en los caracteres seleccionados.
-
Elaboración de tablas de frecuencias mediante la adecuada clasificación de los individuos dentro de cada carácter.
-
Representación grafica de los resultados (elaboración de graficas estadísticas).
-
Obtención de parámetros estadísticos, números que sintetizan los aspectos más relevantes de una distribución estadística.
-
Reordenar los punteos y agruparlos en varias formas para que sea posible tener a primera vista una imagen global de los datos.
-
Construir tablas, graficas y figuras que permitan visualizar los resultados.
-
Convertir los datos originales en formas que sean mas útiles: calificaciones porcentajes
-
Calcular promedios
-
Tomando el promedio como punto de referencia, describir la dispersión de los datos.
-
Obtener una relación entre dos instrumentos de medida diferente.
LA INVESTIGACIÓN ESTADÍSTICA
La investigación estadística es la búsqueda sistematizada y objetiva de hechos o de explicación de fenómenos.
El método de investigación estadística comprende las cinco fases siguientes:
-
Preparación del trabajo.
-
Recopilación de los datos.
-
Evaluación y depuración de los datos.
-
Presentación de los datos.
-
Análisis e interpretación.
PRIMERA FASE O PREPARACION DEL TRABAJO
Se limita a la redacción de las instrucciones para recabar los datos, definición precisa de los datos que se necesitan; diseño de formularios y planillas, planificación y organización del trabajo en el espacio y en el tiempo.
En esta fase deben quedar perfectamente claros los conceptos y cada participante debe conocer a cabalidad sus atribuciones y responsabilidades; ya que las dudas o malas interpretaciones echarán a perder el resto de la investigación.
SEGUNDA FASE O RECOPILACION DE LOS DATOS
En ella se recaban los datos necesarios para la investigación, mediante encuestas, muestreos, censos, o se toman de fuentes secundarias o registros y publicaciones.
La eficiencia con que se realice esta etapa generará la calidad de todo el trabajo de investigación estadística.
1.3.3 TERCERA FASE O EVALUACIÓN DE LOS DATOS
Los datos recopilados, en la vida real, suelen adolecer de imperfecciones y errores varios; debidos a la ignorancia, a malos entendidos, a intereses creados o a prejuicios sociales, de parte de quien aporta los datos o de quien los recaba. De allí que el paso inmediato sería una depuración y evaluación de tales datos, a fin de subsanar o mitigar las influencias y efectos de tales errores e imperfecciones. Para lograrlo se recomiendan los siguientes procedimientos:
-
Revisión total de los cálculos, de las tabulaciones y del procedimiento utilizado.
-
Confrontar los datos recopilados, con los obtenidos al cálculo, con los de otras regiones o países, tomados en otras ocasiones o con otra finalidad.
-
Repetir al muestreo, el mismo trabajo, en zonas estratégicamente escogidas; cuando en las verificaciones anteriores se hubieran obtenido notorias discrepancias.
* Ecuaciones compensadoras:
Se usan para efectuar verificaciones, como las anteriores. Un ejemplo sería la utilizada en censos demográficos, así:
Explicando cada uno de los elementos de la ecuación nos queda entonces que:
Todo referido a un mismo período censal. El resultado así obtenido, debe resultar muy aproximado al obtenido mediante el censo realmente efectuado.
* Índices de preferencia:
Indican la predilección que por determinados dígitos suelen tener los declarantes; lo cual los induce a errores. Al respecto existen varias publicaciones, siendo la más recomendable la de la “Secretaría de la Organización de las Naciones Unidas” (ONU.)
CUARTA FASE O PRESENTACIÓN DE LOS DATOS
Los datos suelen estar presentados en forma tabular, en cuadros de doble entrada, proporcionales, porcentuales, o en valores promedios. También suelen representarse gráficamente, mediante: Histogramas, polígonos, diagramas figurados, prismogramas, pictogramas, dibujos acotados, entre otros.
QUINTA FASE O ANALISIS E INTERPRETACIÓN DE LOS DATOS
Podría decirse que es ésta la fase más amplia de todas y en la cual la investigación rinde sus mejores frutos. Desde la más remota antigüedad se ha venido aplicando el análisis estadístico a las investigaciones demográficas, socioeconómicas, fiscales, entre otros. Obteniéndose así índices y tendencias de natalidad, mortalidad, mortinalidad (nacidos muertos), nupcialidad, inmigración, emigración, etc. De generalización más reciente tenemos los índices y tendencias del costo de la vida, de tan rotunda actualidad; los cuales se obtienen sumando los costos promedios de alimentos, vivienda, medicinas, ropas y servicios consumidos por una persona, familia, estándar, en el período que se estudia. Igualmente, los índices de productividad o relación entre la producción y las horas - hombre de trabajo en ella utilizadas.
La investigación debe desarrollarse sistemáticamente pasando por las etapas de planificación, ejecución y evaluación. En la primera etapa se considera integralmente la investigación, poniéndose por escrito en un documento no solo lo que precede a la obtención de la información en el campo, sino que se toman en cuenta las actividades que se desarrollaran en las etapas restantes.
PLANIFICACIÓN.
-
Justificación de la investigación.
Justificar la investigación significa exponer las razones que fundamentan su realización que en general podrían ser de tipo netamente intelectual o pragmático. En el primer caso podría resultar difícil identificar beneficios, pero en el segundo, los argumentos podrán ser expresados en términos de la utilidad que pudiera reportar tal investigación a la institución en donde se trabaja o al investigador mismo. En cualquier circunstancia, la justificación debe hacerse por escrito para contar, con oportunidad y precisión, con los puntos que habrán de esgrimirse para obtener los recursos necesarios.
-
Planteamiento del problema
Solo cuando el problema este bien enunciado y delimitado será factible localizar todos los posibles antecedentes que bien podrían incluir una investigación que resolviera una pare o la totalidad del problema, aunque también es cierto que tales antecedentes debieran ser enjuiciados para determinar su validez y aplicabilidad a la situación particular que se este manejando.
-
Determinación de los objetivos de la investigación.
Cuando se ha planteado el problema se está en condiciones de decidir si la actual investigación se abocará a la solución parcial o integral del problema y de acuerdo con ello se podrán redactar los objetivos.
Si de acuerdo con la naturaleza de la investigación lo que se pretende es obtener información sobre el estado de las cosas, esto determinara la redacción del o de los objetivos. Si por el contrario, lo que se pretende es probar una hipótesis, el objetivo expresara esa intención.
Debe tenerse en cuenta la posibilidad de que para solucionar el problema planteado en el punto anterior pudiera requerirse la realización de investigaciones previas y que por lo tanto la actual investigación solo constituiría un antecedente indispensable para el desarrollo de lo que pudiese resolver completamente el problema.
-
Definición del universo de estudio.
Con el termino universo se hace referencia al conjunto al cual se le podrán atribuir los resultados, ya sea porque comprende todos los elementos que vayan a ser realmente estudiados o porque habiendo acudido al recurso de examinar solo una muestra, sus integrantes hayan tenido una probabilidad - conocida y distinta a cero - de haber podido formar parte de la muestra. Es necesario que la definición incluya la delimitación precisa del área geográfica y de los requisitos que debe satisfacer cada elemento para considerarlo inequívocamente dentro del universo.
-
Determinación de variables
Las variables no son otra cosa que las características que se van a captar en cada elemento del conjunto y se les denomina así porque no todos los elementos quedan clasificados en la misma categoría o clase. Es frecuente denominar variables independientes a aquellos que podrían causar o influir la variabilidad de otras llamadas variables dependientes. Algunas características importantes son: el peso, la edad, el sexo, la estatura, la presión sanguínea.
Debe hacerse una selección cuidados de las variables que se van a manejar en la investigación teniendo siempre presente los objetivos para no omitir datos importantes y cuidando de no agregar más que los estrictamente necesarios para controlar las actividades de campo.
-
Formulación de hipótesis
Como las hipótesis son enunciados de relaciones entre algunas e las variables, es preciso haber determinado estas para darle un sentido preciso a la relación.
Con frecuencia en la hipótesis se niega lo que se pretende probar obteniendo lo que se denomina una hipótesis de nulidad que constituye el punto de partida para la llamada prueba de hipótesis en estadística.
-
Procedimientos de medición
Una vez identificadas las variables que van a ser analizadas en cada uno de los elementos del conjunto por estudiar, es necesario definirlas estableciendo los procedimientos de medición o en su caso los criterios para establecer la presencia o ausencia de las características.
Conviene destacar que las definiciones deben ser operacionales y no conceptuales, pues, por ejemplo, si una de las variables es obesidad, la definición de que un animal obeso es aquel que tiene un evidente exceso de peso Al que podría considerarse como normal para su estatura, sexo y edad, no establece que procedimientos deben seguirse para calificar al animal como obeso, los cual podría realizarse en términos de que exceda en cierta proporción al peso proporcionado en una tabla o que la piel rebase cierta medida en cierta parte del organismo.
Lo anterior implica que hay que describir la técnica para medir, ya sea peso, estatura, numero de células; para identificar desarrollo de colonias; para establecer la presencia de padecimientos; para identificar preferencias; para conocer puntos de vista, ETC.
-
Selección del diseño.
En el caso de una investigación observacional descriptiva (aquella en la cual se busca obtener información relevante y precisa sobre una situación existente) ocurre que a veces la cobertura es total o sea que se incluye a todo el universo, como en el caso de los censos; pero en otras ocasiones solo se estudio un subconjunto, y los resultados obtenidos se generalizan a todo el universo. En esta situación hay necesidad de utilizar la parte de la estadística que se refiere a los problemas de estimación.
En la investigación observacional analítica (aquella cuyo objetivo es establecer el tipo de asociación que pudiera existir entre dos mas características cuya presencia o ausencia en los elementos de los grupos es ajena a la voluntad del investigador). Y en la experimental (por medio de la cual se analizan los efectos de la exposición o privación intencionada de un factor bien definido en parte de los elementos del conjunto en estudio), el estudio de subconjuntos para generalizar a todo el universo es una necesidad, y los problemas que con tal proceder se generen pueden ser resueltos con la parte de la estadística que se refiere a las pruebas de hipótesis.
-
Procedimientos de captación de la información.
Decididos los datos necesarios debe determinarse cuáles de ellos ya han sido obtenidos, por otro investigador o por otra institución, con las especificaciones requeridas y finalmente establecer para los datos faltantes los mecanismos de captación, que puedan consistir en que el individuo estudiado llene un cuestionario o que un miembro del personal del equipo investigador obtenga la información necesaria; en cualquier caso, habrá que considerar el diseño de un formulario.
-
Procedimientos de elaboración y análisis de la información.
Para garantizar, en los posible que todo el tratamiento de los datos se realizara sin tropiezos es conveniente considerar con anticipación a la captación de los datos cual va a ser el proceso de elaboración de la información, ya que esto puede sugerir la inclusión de un nuevo dato o una manera particular de distribución de los datos en el formulario para facilitar la codificación o la perforación de tarjetas, en el caso en que se decide utilizar la computación electrónica, o establecer alguna actividad de control de calidad de la información del terreno.
-
Programación y conducción de la investigación
Todas las actividades de campo y de oficina deben ser consideradas en su conjunto, permitiendo así establecer la organización detallada de la investigación definiendo las diversas unidades administrativas, las relaciones entre ellas, los procedimientos de trabajo y los recursos necesarios. Entre otras cosas, conviene destacar la importancia de la elaboración del calendario de actividades, de itinerarios cuando sean necesarios, la descripción del flujo de unidades de observación, las precauciones que deben ser tomadas en la aplicación de ciertas técnicas de medición, las medidas que deben tomarse en las situaciones de emergencia que puedan ser anticipadas y particularmente , la forma en que deben ser identificados los elementos del conjunto que sean incluidos como unidades de observación, y en su caso, la forma en que ellos deban ser asignadas a los diferentes tratamientos.
-
Informe de investigación
Conviene esbozar el contenido con que deberá contar el informe. Esto debe incluir la elaboración de un título que explique claramente el contenido del informe, y cuando sea necesario, un subtitulo; una introducción que enuncie el propósito, tópicos y objetivos del estudio, incluyendo donde y cuando se realizo; los elementos estudiados y los métodos; los hallazgos en forma textual concisa o en forma tabular y gráfica cuando sea necesario; discusión de los resultados; el resumen y finalmente los apéndices.
En los apéndices, además de incluir cuadros, definiciones, bibliografías y descripciones de técnicas de medición, se puede agregar un apéndice técnico de circulación restringida en el cual se hagan derivaciones de fórmulas y se den otros resultados de interés, no tanto para los usuarios de esos hallazgos sino para los que necesiten conocer más el proceso de la investigación.
EJECUCIÓN
Poco puede decirse de la ejecución o desarrollo de investigación en general, pues las características de estas quedan determinadas por el tópico, los recursos y la institución que las vaya a realizar; en esta etapa deberá realizarse todo lo planeado en la etapa anterior.
EVALUACIÓN
De toda inversión debe obtenerse cierto rendimiento y la que se hace en investigación no debe ser una excepción, por lo que durante el desarrollo debe irse captando información que permita decidir si se está obteniendo un rendimiento razonable de los recursos, y al final de la investigación deberá establecerse no solo en que medida se lograron los objetivos de la investigación, si no que, comparando el rendimiento de cada uno de los recursos con el que habitualmente debía esperarse, decidir si fue satisfactorio o no y, por último, establecer si la inversión global quedó justificada con los hallazgos finales.
Por lo que se ha dicho de la investigación en general y tomando en cuenta la definición que se dio de estadística, ya deberá resultar evidente que el papel que esta juega en la primera es muy importante en cada una de sus etapas.
Para concluir, la investigación ha de ser un trabajo de equipo, y cuando concurran en una misma persona los dos papeles, el de investigador y el de estadístico, conviene que toda la investigación se discuta con otro investigador o con otro estadístico para no pasar por alto aspectos relevantes.
RECOLECCIÓN Y ORGANIZACIÓN DE DATOS
RECOLECCIÓN:
ENCUESTAS:
Instrumento cuantitativo de investigación social mediante la consulta a un grupo de personas elegidas de forma estadística, realizada con ayuda de un cuestionario.
En poblaciones pequeñas (por ejemplo, los trabajadores de una empresa) se pueden realizar encuestas censales, es decir, a todos los individuos de un colectivo, pero normalmente las encuestas se realizan mediante muestras estadísticamente representativas de una población mayor, para posteriormente extrapolar los resultados al conjunto de la población. La encuesta se diferencia de otros métodos de investigación en que la información obtenida ya está de antemano preparada y estructurada. En este sentido, la encuesta presenta notables limitaciones, al restringir las posibilidades de obtener información a validar o refutar hipótesis previamente establecidas en el cuestionario, coartando el discurso del entrevistado, y sin que resulte posible saber si existe información relevante que no se tiene en cuenta. Además, al tratarse de entrevistas individuales, se pierde la riqueza de fenómenos que resultan de la interacción social.
Según la forma en que se obtienen los datos, las encuestas pueden ser presenciales, telefónicas o postales. Las encuestas presenciales administradas por encuestadores cualificados son las más fiables, exhaustivas y, también, costosas. Por su parte, las encuestas telefónicas permiten una gran rapidez en la obtención de los datos a un bajo coste, pero presentan limitaciones respecto a la duración de la entrevista y un riesgo mayor de sesgo muestral. Los sesgos son precisamente el principal problema a controlar en la realización de una encuesta; pueden provenir de errores muestrales, que dan como resultado una mayor presencia de un grupo de individuos con determinadas características, y/o de la mayor o menor accesibilidad a la entrevista de determinados grupos de personas. También se pueden producir por errores en el cuestionario, que o bien inducen determinadas respuestas, o no tienen en cuenta todas las opciones posibles de los entrevistados. Y, finalmente, pueden aparecer sesgos en el tratamiento estadístico, al establecer las variables a utilizar y al agrupar los datos o los individuos en determinadas categorías.
En cualquier caso, la utilización masiva de las encuestas en procesos de toma de decisiones, tanto en el ámbito publico como privado, ha supuesto una progresiva sistematización de los procesos de trabajo en este tipo de estudios y la creación de normas metodológicas y códigos deontológicos que tratan de asegurar su calidad y consistencia.
ENCUESTA
ESTADÍSTICA DE ESTATURA DE IAFIC
NOMBRE_____________________________________ EDAD______________
CC___________________________________________ SEXO______________
PROGRAMA__________________________________ SEMESTRE_________
PASATIEMPO_______________________________________________________
QUE TIPO DE EJERCICIO REALIZAS___________________________________
____________________________________________________________________
PESO____________Kgs. ESTATURA____________Mts.
FIRMA DEL ENCUESTADO____________________________________________
NOMBRE DEL ENCUESTADOR_________________________________________
FIRMA DEL ENCUESTADOR____________________________________________
ENCUESTA
ESTADÍSTICA DE ESTATURA DE IAFIC
NOMBRE_____________________________________ EDAD______________
CC___________________________________________ SEXO______________
PROGRAMA__________________________________ SEMESTRE_________
PASATIEMPO_______________________________________________________
QUE TIPO DE EJERCICIO REALIZAS___________________________________
____________________________________________________________________
PESO____________Kgs. ESTATURA____________Mts.
FIRMA DEL ENCUESTADO____________________________________________
NOMBRE DEL ENCUESTADOR_________________________________________
FIRMA DEL ENCUESTADOR____________________________________________
TABLAS ESTADÍSTICAS
Las tablas estadísticas son recopilaciones numéricas bien estructuradas y fáciles de interpretar de las que se vale el estadístico para sintetizar los datos obtenidos con el fin de hacer un uso sencillo de ellos o bien para darlos a conocer de forma comprensible.
Existen infinidad de tablas estadísticas, pero las más básicas son las tablas de frecuencias, las de frecuencias relativas y frecuencias acumuladas, las de frecuencias con datos agrupados en intervalos y las de doble entrada.
TABLAS DE FRECUENCIAS
Estas tablas constan de dos columnas. En la primera se escriben los valores de la variable, xi. En la segunda las correspondientes frecuencias, fi. Estas sencillas tablas se utilizan, únicamente, cuando la variable es discreta y admite pocos valores (a lo sumo, de 12 a 16).
La tabla siguiente da la distribución de la variable “número de hijos” correspondiente a un conjunto de 43 familias:
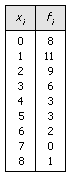
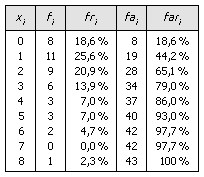
TABLAS DE FRECUENCIAS RELATIVAS Y FRECUENCIAS ACUMULADAS
Una tabla de frecuencias se puede ampliar con nuevas columnas con las frecuencias relativas y las frecuencias acumuladas. La tabla anterior con estos nuevos datos sería:
TABLAS DE FRECUENCIAS CON DATOS AGRUPADOS EN INTERVALOS
Cuando la variable es continua, o es discreta pero toma una gran cantidad de valores, conviene dividir el rango de la variable en unos pocos intervalos (entre 6 y 12) y repartir los valores en ellos. El resultado será una tabla de frecuencias en la cual la variable, en lugar de tomar valores numéricos concretos, varía dentro de intervalos.
Cuando se necesita (por ejemplo para el cálculo de parámetros) que cada intervalo quede representado por un único número, se toma su punto medio, al que se llama marca de clase.
En la tabla adjunta se muestra cómo se han repartido 1.200 calificaciones entre 0 y 10, en 10 intervalos iguales —columna (a). Las marcas de clase (centros de los intervalos) están en la columna (b), las frecuencias en la (c), las frecuencias relativas en la (d), las frecuencias acumuladas en la (e) y las frecuencias acumuladas relativas en la columna (f).
| (a) INTERVALO | (b) MARCA DE CLASES | (c) FRECUENCIA | (d) FECUENCIA RELATIVA | (e) FRECUENCIA ACUMULADA | (f) FRECUENCIA CUMULADA RELATIVA |
| 0-1 | 0.5 | 20 | 0.017 | 20 | 0.017 |
| 1-2 | 1.5 | 15 | 0.012 | 35 | 0.029 |
| 2-3 | 2.5 | 18 | 0.015 | 53 | 0.044 |
| 3-4 | 3.5 | 25 | 0.021 | 78 | 0.065 |
| 4-5 | 4.5 | 44 | 0.037 | 122 | 0.102 |
| 5-6 | 5.5 | 88 | 0.073 | 210 | 0.175 |
| 6-7 | 6.5 | 222 | 0.185 | 432 | 0.360 |
| 7-8 | 7.5 | 335 | 0.279 | 767 | 0.639 |
| 8-9 | 8.5 | 218 | 0.182 | 985 | 0.821 |
| 9-10 | 9.5 | 215 | 0.179 | 1200 | 1000 |
| 1.200 CALIFICACIONES DISTRIBUIDAS EN 10 INTERVALOS | |||||
Tabla de frecuencias con intervalos
Una tabla de distribución de frecuencias sirve para resumir un conjunto de datos estadísticos. Por ejemplo, esta tabla muestra las 1.200 notas o calificaciones recibidas en 4 exámenes por 10 clases de 30 alumnos cada una. La primera columna es la lista de los diez intervalos en que se han agrupado las notas. La segunda columna es el punto medio de cada intervalo. La tercera muestra el número de notas de cada intervalo, es decir, su frecuencia (por ejemplo, hay 20 notas entre 0 y 1). La cuarta es el cociente entre el número de notas en el intervalo y el número total, es decir, la frecuencia relativa (hay 0,017 notas entre 0 y 1 por cada una de las 1.200 notas). La quinta columna es el número de notas en un intervalo y los intervalos menores que él, es decir, la frecuencia acumulada (hay 35 notas menores o iguales que 2). La sexta columna es el cociente entre el número de notas menores o iguales que el intervalo y el número total, es decir, la frecuencia acumulada relativa (0,029 notas entre 0 y 2 por cada una de las 1.200).
TABLAS DE DOBLE ENTRADA
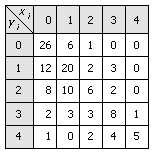
En las distribuciones bidimensionales, en las que a cada individuo le corresponden dos valores, xi, yi, puede suceder que cada par de valores (xm, yn) ocurra varias veces, es decir, lleve apareada una frecuencia. En tal caso conviene disponer los resultados mediante una tabla de doble entrada como la que se muestra a continuación, correspondiente a los resultados de un colectivo de 125 personas puntuadas por su sensibilidad ecológica, xi, y por sus conocimientos de biología, yi:
ORGANIZACIÓN DE DATOS
TABLAS DE DISTRIBUCIÓN DE FRECUENCIAS:
Son tablas que contienen frecuencias absolutas, relativas y acumuladas, maraca de clases y numero de clases.
Son muy útiles para describir el comportamiento de una sola variable.
TABLAS DE CONTINGENCIA:
Son muy útiles cuando se desea examinar o comparar dos o más variables.
CLASES DE FRECUENCIAS
-
FRECUENCIA
El número de veces que ocurre un cierto suceso. Número de elementos comprendidos dentro de un intervalo en una distribución determinada.
Es un numero que nos indica las veces que un dato esta repetido. En una tabla de frecuencias, nos indica la cantidad de datos que están comprendidos en un intervalo de clase.
Es el número de datos o elementos de la muestra, que caen en un mismo intervalo de clase. Es decir, que sus valores quedan totalmente comprendidos dentro de los linderos de ese mismo intervalo.
-
FRECUENCIA ABSOLUTA (ni):
Consiste en la proporción de veces que ocurre dicho suceso con relación al número de veces que podría haber ocurrido.
Puede definirse como el número de veces que se repite cada valor o modalidad de la variable o atributo.
El número de veces que se observa un mismo ítem (Los datos de una misma magnitud o clase), o la cantidad d datos que caen en un mismo intervalo.
La suma de las frecuencias absolutas es igual al tamaño de la población o la muestra.
-
FRECUENCIA RELATIVA (hi):
Es la frecuencia absoluta dividida por el número de casos, es decir la muestra o la población.
Es la relación geométrica entre la frecuencia absoluta y el total de datos. O sea, el cociente de dividir el número de veces que aparece un dato de un intervalo, entre la totalidad de los datos que conforman la muestra de que se trate.
La suma de las frecuencias relativas es igual a la unidad.
Por ejemplo, si una experiencia aleatoria se repite 80 veces y un cierto suceso, S, ocurre 36 veces, decimos que su frecuencia ha sido 36, y su frecuencia relativa 36/80 = 0,45:
f(S) = 36 fr(S) =36/80 = 0,45
La frecuencia relativa también se expresa, en ocasiones, en tantos por ciento (45%).
-
FRECUENCIAS ACUMULADAS (Ni, Hi)
La frecuencia acumulada de una observación de la variable es la suma de las frecuencias correspondientes a los valores menores o anteriores a dicho valor. Es la suma de las frecuencias de un intervalo de clase, con todas las frecuencias de los intervalos que le preceden. Hay dos frecuencias acumuladas que son:
-
Frecuencia absoluta acumulada (Ni)
-
Frecuencia relativa acumulada (Hi)
-
Frecuencia acumulada absoluta
Es la acumulación o suma de todas las frecuencias absolutas hasta el intervalo de clase considerado, inclusive.
-
Frecuencia acumulada relativa
Viene a ser la acumulación de todas las frecuencias relativas hasta el mismo intervalo considerado, inclusive.
En una tabla de frecuencias, cuando la variable es cuantitativa y, por tanto, los distintos valores de la tabla aparecen ordenados de menor a mayor, se llama frecuencia acumulada de un valor de la variable a la suma de su frecuencia con las frecuencias de los valores anteriores. Por ejemplo, si al lanzar un dado 100 veces se obtienen los siguientes resultados:
f(1) = 16 f(2) = 13 f(3) = 21
f(4) = 19 f(5) = 14 f(6) = 17
las frecuencias acumuladas son:
fa(1) = 16 fa(2) = 16 + 13 = 29
fa(3) = 29 + 21 = 50 fa(4) = 50 + 19 = 69
fa(5) = 69 + 14 = 83 fa(6) = 83 + 17 = 100
Estos resultados se aprecian mejor en una tabla:
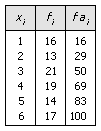
Las frecuencias relativas acumuladas son las frecuencias acumuladas divididas por el número total de individuos.
EJEMPLO:
Supóngase que treinta empleados de acuerdo con el rendimiento al trabajo durante una semana fueron calificados así:
A= Excelente
B= Bueno
C= Aceptable
D= Regular
F=Deficiente
Los resultados fueron:
C - B - C - A - F - A - D - B - D - C - A - B - F - D - C - A -B - D - C - C -B - A - A - C - B - F - A - D - D - F
HALLAR: Las frecuencias (ni), (hi), (Ni), (Hi).
| RENDIMIENTO | TABULACIÓN | ni | hi | Ni | Hi |
| A | /////// | 7 | 0.233 | 7 | 0.233 |
| B | ////// | 6 | 0.20 | 13 | 0.433 |
| C | /////// | 7 | 0.233 | 20 | 0.666 |
| D | ////// | 6 | 0.20 | 26 | 0.866 |
| F | //// | 4 | 0.133 | 30 | 0.999 |
Los datos se pueden ordenar dividiéndolos en clases y registrando el número de observaciones en cada clase.
CLASES
Es un intervalo que contiene un límite inferior y un límite superior.
NUMERO DE CLASES
En una tabla de distribución de frecuencias se puede utilizar la siguiente formula para aproximar el número de clase a utilizar.
nº C= 2C " n
n = Número de la observación
c = Número de clases
El número de clases es la menor potencia a la que se eleva el 2, de tal manera que el resultado será igual o mayor al número de observaciones.
INTERVALO DE CLASES (IC)
Es el rango de valores encontrados dentro de una clase.
IC = valor mayor - valor menor IC = v> - v<
Número deseado de clases c
EJEMPLO:
El siguiente conjunto de datos corresponde al número de pasajeros que han decidido viajar en la línea aérea T & T, correspondiente a los últimos 50 días.
68
72
50
70
65
83
77
79
80
93
71
74
60
84
72
84
73
81
84
92
77
57
70
59
85
74
78
79
91
102
83
67
66
75
79
82
93
99
101
80
79
69
76
94
71
97
95
83
86
69
Se pide ordenar los datos mediante una tabla de distribución de frecuencias:
n = 50 días
26 " 50 IC = 102 - 50
c = 6 64 " 50 6
IC = 8.6 pasajeros
IC = ~ 10
| CLASES | FRECUENCIA ABSOLUTA | FRECUENCIA RELATIVA | FRECUENCIA ACUMULADA | F. RELATIVA ACUMULADA | MARCA DE CLASE. |
| (PASAJEROS) | (DÍAS) | (%) | (DÍAS) | (%) | (PASAJEROS) |
| 50 - 59 | 3 | 0.06 | 3 | 0.06 | 54.5 |
| 60 - 69 | 7 | 0.14 | 10 | 0.20 | 64.5 |
| 70 -79 | 18 | 0.36 | 28 | 0.56 | 74.5 |
| 80 -89 | 12 | 0.24 | 40 | 0.86 | 84.5 |
| 90 -99 | 8 | 0.16 | 48 | 0.96 | 94.5 |
| 100 -109 | 2 | 0.04 | 30 | 1.00 | 104.5 |
TABLA DE FRECUENCIA ACUMULADA “MENOR DE”
| CLASES | FRECUENCIA ABSOLUTA | F. ACUMULADA MENOR DE (DIAS) |
| MENOS DE 50 | 0 | 0 |
| MENOS DE 60 | 3 | 3 |
| MENOS DE 70 | 7 | 10 |
| MENOS DE 80 | 18 | 28 |
| MENOS DE 90 | 12 | 40 |
| MENOS DE 100 | 8 | 48 |
| MENOS DE 110 | 2 | 50 |
INTERPRETACIÓN
La tabla muestra que en ningún momento volaron menos de cincuenta pasajeros, la frecuencia acumulada de la primera clase es cero. En tres días menos de sesenta pasajeros abordaron, por eso la frecuencia acumulada de la segunda clase es tes. Debido a que hubo diez días en los cuales menos de setenta pasajeros volaron, la frecuencia acumulada de la tercera clase es 3 + 7 = 10. la frecuencia acumulada de las clases restantes se determinan de manera similar.
TABLA DE FRECUENCIA ACUMULADA “MAYOR DE”
| CLASES | FRECUENCIA ABSOLUTA | F. ACUMULADA MAYOR DE (DIAS) |
| 50 O MAS | 3 | 50 |
| 60 O MAS | 7 | 47 |
| 70 O MAS | 18 | 40 |
| 80 O MAS | 12 | 22 |
| 90 O MAS | 8 | 10 |
| 100 O MAS | 2 | 2 |
| 110 O MAS | 0 | 0 |
INTERPRETACIÓN
En los cincuenta días, por lo menos cincuenta pasajeros abordaron la aerolínea, por lo tanto la frecuencia acumulada de la primera clase es cincuenta. En tres de esos días menos de sesenta pasajeros abordaron, por tanto la frecuencia acumulada de la segunda clase es 50 - 3 = 47. debido a que el número de pasajeros fue menor de setenta en diez días, la frecuencia acumulada para la tercera clase es igual a 50 - 10 = 40. la frecuencia acumulada para las clases restantes se determinan de manera similar.
GRÁFICOS ESTADÍSTICOS
Representaciones gráficas de los resultados que se muestran en una tabla estadística. Pueden ser de formas muy diversas, pero con cada tipo de gráfica se cumple un propósito. Por ejemplo, en los medios de comunicación, libros de divulgación y revistas especializadas se encuentran multitud de gráficas estadísticas en las que, con notable expresividad, se ponen de manifiesto los rasgos de la distribución que se pretende destacar. Los diagramas de barras, los diagramas de sectores, los histogramas y los polígonos de frecuencias son algunas de ellas.
Los gráficos sirven para percibir más fácilmente las características esenciales de una distribución de frecuencias y comparar una distribución con otra, si se desea. Estas graficas no deben ser consideradas como sustitutivos del tratamiento estadístico de los datos, sino más bien como ayudas visuales para pensar en los problemas estadísticos y para discutirlos más fácilmente.
Los gráficos se han de explicar enteramente por sí mismos. El contenido de un gráfico deberá ser tan completo como sea posible. Las escalas vertical y horizontal estarán rotuladas con claridad dando las unidades pertinentes. La mayoría de los gráficos presentan información numérica con escalas, que deben rotularse para describir completamente la variable presentada en la escala y para variables de medida se dirán las unidades de medición. No se debe tratar de abarcar demasiada información en un solo gráfico. Es mejor hacer varios gráficos que comprimir toda la información en uno solo. Una regla práctica segura es evitar gráficos que contengan más de 3 curvas. Los gráficos tienen que dar una visión general y no una imagen detallada de un conjunto de datos. Las presentaciones detalladas se deben reservar para las tablas. Las tablas se explicarán por sí mismas enteramente. Como los gráficos, se ha de dar suficiente información en el título y en los encabezamientos de columnas y filas de la tabla para permitir que el lector identifique fácilmente su contenido. Como el título será por lo general lo primero que se lee en detalle, deberá suministrar toda la información esencial sobre el contenido de la tabla y deberá especificar el tiempo, lugar, material ó estudio experimental y relaciones que se presenten en la tabla. Para cada variable numérica se han de dar las unidades. La función del rayado es dar claridad de interpretación. Las anotaciones de numéricas del cero se han de escribir explícitamente. Una anotación numérica no debe comenzar con un punto decimal. Los números que indican valores de la misma característica se han de dar con el mismo número de decimales.
EMPLEO ERRÓNEO DE LAS TÉCNICAS DE REPRESENTACIÓN GRÁFICA…
Las graficas han sido empleadas algunas veces por los negocios comerciales para tratar de confundir al lector. Por ejemplo, si se manipulan intencionadamente los ejes de una gráfica, el vertical (de las coordenadas o eje y) y el horizontal (de las abscisas o eje x), es posible dar la impresión que se desee.
Esta gráfica muestra dos diagramas de barras (basados en los mismos datos) en los cuales se alargaron las ordenadas y las abscisas, respectivamente, para causar dos impresiones distintas.
En la grafica a tiende a exagerar la diferencia entre las frecuencias de las tres clases, mientras que la b tiende a reducirla al mínimo.
El uso de estos artificios es totalmente opuesto al propósito de un estadístico, que es el de presentar unos datos con tal claridad que las interpretaciones equivocas sean mínimas.
Para evitar una anarquía en la técnica de representación gráfica, es necesario adoptar un convenio para minimizar la posibilidad de interpretaciones erróneas. La mayor parte de los estadísticos coinciden en que la altura de la gráfica debe ser de aproximadamente 0.75 de su longitud, siendo aceptable que esta proporción esté comprendida entre 0.70 y 0.80.
DIAGRAMA DE BARRAS
En este tipo de gráfica, sobre los valores de las variables se levantan barras estrechas de longitudes proporcionales a las frecuencias correspondientes. Se utilizan para representar variables cuantitativas discretas.
Los diagramas de barras pueden ser de diferentes tipos: de barras simples, de barras múltiples, o de barras compuestas
Las barras pueden representarse horizontalmente. La ventaja de la horizontalidad estriba en que es más fácil añadir leyendas.
Recibe el nombre de diagrama de barras el gráfico que asocia a cada valor de la variable una barra, generalmente vertical, proporcional a la frecuencia (o a la cantidad) con que se presenta.
Requisitos para realizar un diagrama de barras:
1- texto visible
2- separación de las barras menor que su ancho
3- escala presente
4- se comparan longitudes de rectángulos.
El diagrama de barras siguiente representa la distribución del número de hijos de 43 familias:
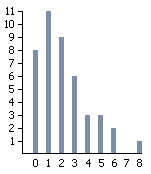
El diagrama de barras es parecido a un histograma, puede mostrar cantidades o porcentajes para dos o más variables en el eje vertical.
-
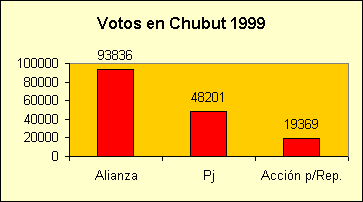
Gráficos de barras verticales
(Llamados por algunos software de columnas)
Representan valores usando trazos verticales, aislados o no unos de otros, según la variable a graficar sea discreta o continua. Pueden usarse para representar:
-
una serie
-
dos o más series (también llamado de barras comparativas)
-
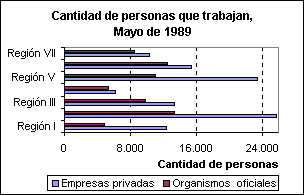
Gráficos de barras horizontales
Representan valores discretos a base de trazos horizontales, aislados unos de otros. Se utilizan cuando los textos correspondientes a cada categoría son muy extensos.
-
para una serie
-
para dos o más series
-
Gráficos de barras proporcionales
Se usan cuando lo que se busca es resaltar la representación de los porcentajes de los datos que componen un total.
Las barras pueden ser:
-
Verticales
-
Horizontales

-
Gráficos de barras comparativas
Se utilizan para comparar dos o más series, para comparar valores entre categorías.
Las barras pueden ser:
-
Verticales
-
horizontales

-
Gráficos de barras apiladas
Se usan para mostrar las relaciones entre dos o más series con el total.
Las barras pueden ser:
-
verticales
-
horizontales

HISTOGRAMA
Los histogramas se utilizan para representar tablas de frecuencias con datos agrupados en intervalos. Si los intervalos son todos iguales, cada uno de ellos es la base de un rectángulo cuya altura es proporcional a la frecuencia correspondiente. El histograma que se muestra a continuación es el correspondiente a la tabla de frecuencias con intervalos (1.200 calificaciones distribuidas en 10 intervalos):
|
|
El histograma es un grafico constituido por rectángulos en donde se colocan las clases de una distribución de frecuencias en el eje horizontal y las frecuencias absolutas en el eje vertical. En la parte superior de cada rectángulo va la frecuencia relativa de cada clase.
Es una de las tantas formas gráficas de representar la distribución de frecuencias, consistente en rectángulos o barras proporcionales.
Para dibujar el gráfico o histograma, se medirán los intervalos de clase en el eje de las abscisas de un plano cartesiano, y las frecuencias de cada intervalo, sobre el eje de las ordenadas, en forma de barras.

El principio de representación que rige la construcción del histograma es que la superficie de cada rectángulo sea proporcional a la frecuencia de la clase que representa, según una constante de proporcionalidad fija e igual para todas las clases; cuando, como es habitual, las clases son todas ellas de la misma amplitud, este principio se traduce en que la altura de cada rectángulo representa directamente la frecuencia de la clase correspondiente.
INTERPRETACIÓN
En la grafica se puede observar que ningún día volaron menos de cincuenta pasajeros, y tampoco volaron más de ciento diez pasajeros. En dieciocho días volaron entre setenta y ochenta pasajeros que equivale al 36%, en tres días volaron entre cincuenta y sesenta pasajeros los cuales equivalen al 6%, y en dos días volaron entre cien y ciento diez pasajeros lo cual equivales al 4%.
POLÍGONOS DE FRECUENCIA
En el eje horizontal se colocan los puntos medios de cada clase y en el eje vertical la frecuencia absoluta.
Las distribuciones de frecuencias pueden ser representadas mediante tablas o mediante histogramas. Otra forma gráfica de representación la constituyen los polígonos de frecuencias. Para dibujarlos, se levantan en cada uno de los puntos medios de clase, ordenadas iguales a las frecuencias de cada intervalo de clase respectivo, es decir, que las abscisas serán iguales a los puntos medios de clase, y las ordenadas a las frecuencias.
Para que cierre el polígono se toman los puntos medios de clase inferior y superior a la muestra, con frecuencias CERO; es decir: Sobre el mismo eje de las equis.
Si se unen entre si consecutivamente los puntos medios de las bases superiores de los rectángulos de un histograma, se obtiene una línea poligonal denominada polígono de frecuencias. Esta línea acostumbra prolongarse por sus extremos hasta cortar el eje de abscisas. Para ello, se toman dos intervalos de clase que no contienen valores de la variable, uno situado por debajo del extremo inferior del rango de variable y a continuación de él, y el otro, a continuación del extremo superior del rango y por encima de el, ambos de igual amplitud que las restantes clases; la línea poligonal se cierra entonces prolongándola por cada lado hasta unirla con los puntos medios de estos dos intervalos. De esta manera se consigue que el área de la superficie encerrada por el polígono de frecuencias y el eje de abscisas sea igual a la suma de las áreas de los rectángulos que integran el histograma correspondiente, de modo que ambas representaciones resultan ser equivalentes.

INTERPRETACIÓN
En la grafica se puede observar que ningún día volaron menos de cincuenta pasajeros, y tampoco volaron más de ciento diez pasajeros. En dieciocho días volaron entre setenta y ochenta pasajeros que equivale al 36%, en tres días volaron entre cincuenta y sesenta pasajeros los cuales equivalen al 6%, y en dos días volaron entre cien y ciento diez pasajeros lo cual equivales al 4%.
FORMAS DE LOS POLÍGONOS DE FRECUENCIA
Los polígonos de frecuencias pueden tomar un número ilimitado de formas. No obstante, muchos de los procedimientos estadísticos estudiados suponen una forma particular de distribución que es la curva normal que toma “forma de campana.
-
Distribución leptocúrtica caracterizada por una concentración de datos en el centro de la distribución.
-
Distribución mesocúrtica: toma la forma ideal de la curva normal.
-
Platicúrtica: predomina el caso opuesto a la Distribución leptocúrtica.
Se dice que la curva normal es una distribución simétrica, porque si la dobla por la mitad, ambas partes coinciden. Sin embargo, no todas las curvas simétricas tienen forma de campana.
A ciertas distribuciones se les ha dado nombres particulares: distribución rectangular, distribución en u, distribución bimodal.
Cuando una distribución no es simétrica se dice que es sesgada. Al decir que una distribución es positivamente sesgada queremos decir que decae hacia el extremo derecho del eje horizontal y que relativamente hay un número menor de frecuencias en ese extremo. Si, por el contrario decimos que una distribución es negativamente sesgada queremos decir que hay relativamente menos datos asociados con el lado izquierdo del eje horizontal.
HISTOGRAMA Y POLÍGONOS DE FRECUENCIAS ACUMULADAS
Si se representan las frecuencias acumuladas de una tabla de datos agrupados se obtiene el histograma de frecuencias acumuladas o su correspondiente polígono. He aquí los que se obtienen de la tabla de 1.200 calificaciones:
|
|
DIAGRAMA CIRCULAR
En un diagrama de este tipo, los 360º de un círculo se reparten proporcionalmente a las frecuencias de los distintos valores de la variable.
Se trata de representar, mediante un círculo, la totalidad o el 100% de los datos de la muestra y, en el mismo, mediante sectores circulares, proporcionalmente, se representarán los valores parciales. A tal efecto, se pueden obtener en el mercado, transportadores especiales, graduados en por cientos.
Resultan muy adecuados cuando hay pocos valores, o bien cuando el carácter que se estudia es cualitativo. El diagrama de sectores siguiente refleja el resultado de una encuesta (realizada a 300 personas) sobre los tipos de película preferidos por el público en general:
|
|
El diagrama circular es de especial utilidad para mostrar proporciones o porcentajes relativos de una variable. Se construye marcando una porción del círculo correspondiente a cada categoría de la variable.
INTERPRETACIÓN
En la grafica se puede observar que ningún día volaron menos de cincuenta pasajeros, y tampoco volaron más de ciento diez pasajeros. En dieciocho días volaron entre setenta y ochenta pasajeros que equivale al 36%, en tres días volaron entre cincuenta y sesenta pasajeros los cuales equivalen al 6%, y en dos días volaron entre cien y ciento diez pasajeros lo cual equivales al 4%.
OJIVAS
Cuando se trata de relacionar observaciones en un mismo aspecto para dos colectivos diferentes no es posible ejecutar comparaciones sobre la base de la frecuencia, es necesario tener una base estándar, la frecuencia relativa. La ojiva representa gráficamente la forma en que se acumulan los datos y permiten ver cuantas observaciones se hallan por arriba o debajo de ciertos valores. Es útil para obtener una medida de los cuartiles, deciles, percentiles.
OJIVA DE FRECUENCIA ACUMULADA MENOR DE
Se grafica colocando en el eje horizontal las clases de una distribución de frecuencia acumulada menor de y en el eje vertical las frecuencias acumuladas menor de.
| CLASES | FRECUENCIA ABSOLUTA | F. ACUMULADA MENOR DE (DIAS) |
| MENOS DE 50 | 0 | 0 |
| MENOS DE 60 | 3 | 3 |
| MENOS DE 70 | 7 | 10 |
| MENOS DE 80 | 18 | 28 |
| MENOS DE 90 | 12 | 40 |
| MENOS DE 100 | 8 | 48 |
| MENOS DE 110 | 2 | 50 |
OJIVA DE FRECUENCIA ACUMULADA MAYOR DE
Se grafica colocando en el eje horizontal las clases de una distribución de frecuencia acumulada mayor de y en el eje vertical las frecuencias acumuladas mayor de.
| CLASES | FRECUENCIA ABSOLUTA | F. ACUMULADA MAYOR DE (DIAS) |
| 50 O MAS | 3 | 50 |
| 60 O MAS | 7 | 47 |
| 70 O MAS | 18 | 40 |
| 80 O MAS | 12 | 22 |
| 90 O MAS | 8 | 10 |
| 100 O MAS | 2 | 2 |
| 110 O MAS | 0 | 0 |
DIAGRAMA DE SECTORES
En los gráficos de diagramas de sectores cada suceso viene representado por un sector circular de una amplitud proporcional a su frecuencia.
La amplitud de cada sector circular se obtiene mediante una simple regla de tres.
Cuando estos diagramas se utilizan para comparar magnitudes en distintos períodos o para diferentes lugares (por ejemplo países), a cada círculo hay que asignarle una superficie proporcional a la magnitud que representa.
DIAGRAMA DE CURVAS
Una curva es una representación gráfica de las relaciones entre variables.
En estadística se emplean muchos tipos de curvas, dependiendo de la naturaleza de los datos y del propósito para el que la curva ha sido proyectada.
DIAGRAMAS DE LINEAS
En este tipo de gráfico se representan los valores de los datos en dos ejes cartesianos ortogonales entre sí.
Se pueden usar para representar:
-
una serie
-
dos o más series

Estos gráficos se utilizan para representar valores con grandes incrementos entre sí.

GRÁFICOS DE ÁREAS
En estos tipos de gráficos se busca mostrar la tendencia de la información generalmente en un período de tiempo.
Pueden ser:
-
Para representar una serie
-
para representar dos o más series
-
en dos dimensiones
-
en tres dimensiones.

CARTOGRAMAS
Estos tipos de gráficos se utilizan para mostrar datos sobre una base geográfica. La densidad de datos se puede marcar por círculos, sombreado, rayado o color.

GRÁFICOS MIXTOS
En estos tipos de gráficos se representan dos o más series de datos, cada una con un tipo diferente de gráfico. Son gráficos más vistosos y se usan para resaltar las diferencias entre las series.
Pueden ser:
-
en dos dimensiones
-
en tres dimensiones.

OTROS GRÁFICOS
En esta categoría se encuentran la mayoría de los gráficos utilizados en publicidad. Se los complementa con un dibujo que esté relacionado con el origen de la información a mostrar. Son gráficos llamativos, atraen la atención del lector.
DISPERSOGRAMA
Son gráficos que se construyen sobre dos ejes ortogonales de coordenadas, llamados cartesianos, cada punto corresponde a un par de valores de datos x e y de un mismo elemento suceso.

PICTOGRAMAS
Los pictogramas son gráficos similares a los gráficos de barras, pero empleando un dibujo en una determinada escala para expresar la unidad de medida de los datos. Generalmente este dibujo debe cortarse para representar los datos.
Es común ver gráficos de barras donde las barras se reemplazan por dibujos a diferentes escalas con el único fin de hacer más vistoso el gráfico, estos tipos de gráficos no constituyen un pictograma.
Pueden ser:
-
En dos dimensiones
-
En tres dimensiones.

TABULACIÓN ENCUESTAS
ESTATURA PROMEDIO DE LA FACULTAD DE VETERINARIA
Se realizaron 50 encuestas a estudiante de la facultad de veterinaria en la universidad de IAFIC para conocer su estatura promedio en metros, en la siguiente tabla se observa a la cantidad de personas que se les realizaron las preguntas por semestre, para que del total de 50 estudiantes:
| CANTIDAD DE ESTUDIANTES | ||||
| SEMESTRE | Hombres | f. relativa | Mujeres | f. relativa |
| 1 | 2 | 0.04 | 0 | 0 |
| 2 | 4 | 0.08 | 3 | 0.06 |
| 3 | 3 | 0.06 | 3 | 0.06 |
| 4 | 3 | 0.06 | 4 | 0.08 |
| 5 | 6 | 0.12 | 0 | 0 |
| 6 | 5 | 0.1 | 1 | 0.02 |
| 7 | 3 | 0.06 | 2 | 0.04 |
| 8 | 4 | 0.08 | 2 | 0.04 |
| 9 | 2 | 0.04 | 1 | 0.02 |
| 10 | 2 | 0.04 | 0 | 0 |
| TOTAL | 34 | 0.68 | 16 | 0.32 |
INTERPRETACIÓN:
El cuadro nos muestra que hay mas hombres que mujeres en la facultad de Medicina Veterinaria, ya que el genero masculino representa un mayor porcentaje, respecto a las mujeres.
Los resultados de las 50 encuestas realizadas para conocer la estatura promedio de los estudiantes de medicina veterinaria de la universidad IAFIC se pueden observar en la siguiente tabla:
| 1,54 | 1,62 | 1,68 | 1,74 | 1,80 |
| 1,55 | 1,64 | 1,68 | 1,75 | 1,80 |
| 1,56 | 1,65 | 1,69 | 1,75 | 1,82 |
| 1,58 | 1,65 | 1,69 | 1,78 | 1,82 |
| 1,58 | 1,65 | 1,70 | 1,79 | 1,84 |
| 1,59 | 1,65 | 1,71 | 1,80 | 1,85 |
| 1,61 | 1,65 | 1,72 | 1,80 | 1,87 |
| 1,62 | 1,65 | 1,72 | 1,80 | 1,89 |
| 1,62 | 1,66 | 1,72 | 1,80 | 1,89 |
| 1,62 | 1,68 | 1,74 | 1,80 | 1,96 |
NÚMERO DE CLASES
N°C = 2C " n = 26 " 50 = 64 " 50
INTERVALO DE CLASES
IC = valor mayor - valor menor IC = v> - v<
Número deseado de clases c
IC = 1.96 - 1.54 IC = 7 METROS.
6
| CLASES | FRECUENCIA ABSOLUTA | FRECUENCIA RELATIVA | FRECUENCIA ACUMULADA | F. RELATIVA ACUMULADA | MARCA DE CLASE. |
| (METROS) | (PERSONAS) | (%) | (PERSONAS) | (%) | (METROS) |
| 1.54 - 1.61 | 7 | 0.14 | 7 | 0.14 | 1.575 |
| 1.62 - 1.69 | 17 | 0.34 | 24 | 0.48 | 1.655 |
| 1.70 - 1.77 | 9 | 0.18 | 33 | 0.66 | 1.735 |
| 1.78 - 1.85 | 13 | 0.26 | 46 | 0.92 | 1.815 |
| 1.86 - 1.93 | 3 | 0.06 | 49 | 0.98 | 1.895 |
| 1.94 - 2.01 | 1 | 0.02 | 50 | 1.00 | 1.975 |
TABLA DE FRECUENCIA ACUMULADA MENOR DE…
| CLASES | FRECUENCIA ABSOLUTA (personas) | F. ACUMULADA MENOR DE (personas) |
| MENOS DE 1.54 | 0 | 0 |
| MENOS DE 1.62 | 7 | 7 |
| MENOS DE 1.70 | 17 | 24 |
| MENOS DE 1.78 | 9 | 33 |
| MENOS DE 1.86 | 13 | 46 |
| MENOS DE 1.94 | 3 | 49 |
| MENOS DE 2.02 | 1 | 50 |
INTERPRETACIÓN
La tabla muestra que en ninguna persona mide menos de 1.54 metros, por lo tanto la frecuencia acumulada es 0; 7 personas miden menos de 1.62 metros por lo que corresponde a la frecuencia acumulada de 7; la frecuencia acumulada de la tercera clase es 24 ya que 17 personas miden menos de 1.70 metros; 9 personas miden menos de 1.78 metros por lo que les corresponde la frecuencia acumulada de 33; la quinta clase indica que 13 personas miden menos de 1.86 metros por lo que les corresponde la frecuencia acumulada de 46; 3 personas miden menos de 1.94 metros por lo cual la frecuencia acumulada es 49; la ultima clase indica que solo una persona mide menos de 2.02 metros, la frecuencia acumulada es 50.
TABLA DE FRECUENCIA ACUMULADA MAYOR DE…
| CLASES | FRECUENCIA ABSOLUTA | F. ACUMULADA MAYOR DE (DIAS) |
| 1.54 O MAS | 7 | 50 |
| 1.62 O MAS | 17 | 43 |
| 1.70 O MAS | 9 | 26 |
| 1.78 O MAS | 13 | 17 |
| 1.86 O MAS | 3 | 4 |
| 1.94 O MAS | 1 | 1 |
| 2.02 O MAS | 0 | 0 |
INTERPRETACIÓN
La tabla muestra que 7 personas miden 1.54 metros o mas, por lo tanto la frecuencia acumulada es 50; 17 personas miden 1.62 metros o mas por lo que corresponde a la frecuencia acumulada de 43; la frecuencia acumulada de la tercera clase es 26 ya que 9 personas miden 1.70 metros o mas; 13 personas miden 1.78 metros o mas por lo que les corresponde la frecuencia acumulada de 17; la quinta clase indica que 3 personas miden 1.86 metros o mas por lo que les corresponde la frecuencia acumulada de 4; 1 persona mide 1.94 metros o mas por lo cual la frecuencia acumulada es 1; la ultima clase indica que ninguna persona mide 2.02 metros o mas, por ende, la frecuencia acumulada d esta clase es 0.
TABLA DE CONTINGENCIA…
| HOMBRES | MUJERES | |||
| CLASES | FRECUENCIA ABSOLUTA | FRECUENCIA RELATIVA | FRECUENCIA ABSOLUTA | FRECUENCIA RELATIVA |
| 1.54 - 1.61 | 0 | 0 | 7 | 0.14 |
| 1.62 - 1.69 | 12 | 0.24 | 5 | 0.1 |
| 1.70 - 1.77 | 6 | 0.12 | 4 | 0.08 |
| 1.78 - 1.85 | 12 | 0.24 | 0 | 0 |
| 1.86 - 1.93 | 3 | 0.06 | 0 | 0 |
| 1.94 - 2.01 | 1 | 0.02 | 0 | 0 |
| TOTAL | 34 | 0.68 | 16 | 0.32 |
INTERPRETACIÓN
La tabla muestra que no hay hombres que midan entre 1.54 y 1.61 metros, mientras que hay 7 mujeres que están en esta clase por lo que la frecuencia relativa de las mujeres es 0.14%; entre 1.62 y 1.69 metros, hay 12 hombres por lo que la frecuencia relativa es 0.24%, mientras que hay 5 mujeres que están en esta clase por lo que la frecuencia relativa de las mujeres es 0.1%; entre 1.70 y 1.77 metros, hay 6 hombres por lo que la frecuencia relativa es 0.12%, mientras que hay 4 mujeres que están en esta clase por lo que la frecuencia relativa de las mujeres es 0.08%; entre 1.78 y 1.85 metros hay 12 hombres por lo cual la frecuencia relativa de esta clase es 0.24%; entre 1.86 y 1.93 metros hay 3 hombres por lo que la frecuencia relativa es 0.06%; y en la ultima clase que es entre 1.94 y 2.01 metros hay un solo hombre por lo que le corresponde una frecuencia relativa de 0.02%, en las ultimas 3 clases no hay ninguna mujer que clasifique, por ende, la frecuencia relativa para estas clases, respecto a las mujeres es 0%.
CANTIDAD DE ESTUDIANTES ENCUESTADOS POR SEMESTRE!!!
HISTOGRAMA ESTATURA PROMEDIO DE LA FACULTAD!!!
INTERPRETACIÓN
El grafico muestra que 7 personas, es decir, el 14% de los encuestados miden entre 1.54 y 1.61 metros, mientras que; entre 1.62 y 1.69 metros, hay 17 personas lo que equivale al 34% total de los encuestados; hay 9 personas que mides entre 1.70 y 1.77 metros lo que equivale al 18%, entre 1.78 y 1.85 metros hay 13 personas lo que corresponde al 26%; ; entre 1.86 y 1.93 metros hay 3 personas lo que equivale al 6%; y en la ultima clase que es entre 1.94 y 2.01 metros hay una sola persona por ende, le corresponde el 2%.
POLÍGONO DE FRECUENCIAS ESTATURA PROMEDIO DE LA FACULTAD!!!
INTERPRETACIÓN
El grafico muestra que 7 personas miden entre 1.54 y 1.61 metros, mientras que; entre 1.62 y 1.69 metros, hay 17 personas; hay 9 personas que mides entre 1.70 y 1.77 metros, entre 1.78 y 1.85 metros hay 13 personas; entre 1.86 y 1.93 metros hay 3 personas; y en la ultima clase que es entre 1.94 y 2.01 metros hay una sola persona.
DIAGRAMA CIRCULAR ESTATURA PROMEDIO DE LA FACULTAD!!!
INTERPRETACIÓN
El grafico muestra que el 14% de los encuestados miden entre 1.54 y 1.61 metros, mientras que el 34% mide entre 1.62 y 1.69 metros, el 18% miden entre 1.70 y 1.77 metros , el 26% de los encuestados miden entre 1.78 y 1.85 metros; el 6% mide entre 1.86 y 1.93 metros y solo el 2% mide entre 1.94 y 2.01.
DIAGRAMA DE BARRAS ESTATURA HOMBRES Y MUJERES EN LA FACULTAD!!!
INTERPRETACIÓN
El grafico muestra que no hay hombres que midan entre 1.54 y 1.61 metros, mientras que hay 7 mujeres que están en esta clase; entre 1.62 y 1.69 metros, hay 12 hombres mientras que hay 5 mujeres que están en esta clase; entre 1.70 y 1.77 metros, hay 6 hombres, mientras que hay 4 mujeres que están en esta clase; entre 1.78 y 1.85 metros hay 12 hombres; entre 1.86 y 1.93 metros hay 3 hombres y en la ultima clase que es entre 1.94 y 2.01 metros hay un solo hombre, en las ultimas 3 clases no hay ninguna mujer que clasifique.
OJIVA FRECUENCIA ACUMULADA MENOR DE!!!
INTERPRETACIÓN
El grafico muestra que ninguna persona mide menos de 1.54 metros, por lo tanto la frecuencia relativa es 0; 7 personas miden menos de 1.62 metros por lo que corresponde a la frecuencia relativa de 7; la frecuencia relativa de la tercera clase es 24 ya que 17 personas miden menos de 1.70 metros; 9 personas miden menos de 1.78 metros por lo que les corresponde la frecuencia acumulada de 33; la quinta clase indica que 13 personas miden menos de 1.86 metros por lo que les corresponde la frecuencia acumulada de 46; 3 personas miden menos de 1.94 metros por lo cual la frecuencia acumulada es 49; la ultima clase indica que solo una persona mide menos de 2.02 metros, la frecuencia acumulada es 50.
OJIVA FRECUENCIA ACUMULADA MAYOR DE!!!
INTERPRETACIÓN
El grafico muestra que 7 personas miden 1.54 metros o mas, por lo tanto la frecuencia acumulada es 50; 17 personas miden 1.62 metros o mas por lo que corresponde a la frecuencia acumulada de 43; la frecuencia acumulada de la tercera clase es 26 ya que 9 personas miden 1.70 metros o mas; 13 personas miden 1.78 metros o mas por lo que les corresponde la frecuencia acumulada de 17; la quinta clase indica que 3 personas miden 1.86 metros o mas por lo que les corresponde la frecuencia acumulada de 4; 1 persona mide 1.94 metros o mas por lo cual la frecuencia acumulada es 1; la ultima clase indica que ninguna persona mide 2.02 metros o mas, por ende, la frecuencia acumulada d esta clase es 0.
CONCLUSIONES
La estadística es una agrupación de datos ordenados en forma sistemática en cuadros y/o gráficos. La estadística puede representarse como descriptiva o inferencial.
Cuando coloquialmente se habla de estadística, se suele pensar en una relación de datos numéricos presentada de forma ordenada y sistemática. Esta idea es la consecuencia del concepto popular que existe sobre el término y que cada vez está más extendido debido a la influencia de nuestro entorno, ya que hoy día es casi imposible que cualquier medio de difusión, periódico, radio, televisión, etc, no nos aborde diariamente con cualquier tipo de información estadística sobre accidentes de tráfico, índices de crecimiento de población, turismo, tendencias políticas, etc.
La estadística descriptiva describe el comportamiento de un hecho a través de la recopilación, ordenamiento, clasificación y representación mediante cuadros y gráficos de los datos en estudio, con la finalidad de analizarlos e interpretarlos utilizando medidas.
La estadística inferencial es aquella técnica aplicada a investigaciones parciales denominadas muestras. Que permiten la obtención de ciertos resultados mediante la aplicación de medidas.
Estadísticas son todas aquellas informaciones que aparecen en publicaciones en forma de cifras, cuadros o gráficos, los cuales han sido ordenados en forma sistemática, para mostrar el comportamiento de un hecho que ha sido objeto de un estudio.
La población es el conjunto de todos los elementos cuyo conocimiento interesa a cada uno de esos elementos.
La muestra es un conjunto de individuos extraídos de una población con el fin de inferir, mediante su estudio características de toda la población.
La variable es una propiedad con respecto a la cual los individuos de una muestra difieren de algún modo verificable.
Para la planificación de un estudio estadístico se deben considerar las siguientes actividades:
DETERMINACIÓN DE LOS OBJETIVOS DE LA INVESTIGACIÓN: esto es claramente una atribución del investigador, pero como constituye el punto de partida para definir y decidir tanto universo como variables y hasta el mismo diseño, el estadístico debe conocerlos y es frecuentemente él quien contribuye a precisar los objetivos anticipando las dificultades para obtener cierta información, identificando imprecisiones que no le permitan decidir que conjunto va a ser investigado o cuestionado el que realmente debe obtenerse la información que queda implicada en los objetivos.
DEFINICIÓN DEL UNIVERSO EN ESTUDIO: Como lo más frecuente es que deba estudiarse solo parte del universo, el estadístico va a requerir cierta información previa sobre el conjunto total para poder utilizar algún medio objetivo de seleccionar las unidades que van a ser realmente estudiadas. Tal información constituye el marco muestral que normalmente no existe para todos los elementos del conjunto o no existe en absoluto, lo cual influenciará los costos y el diseño de la investigación y a veces se traduce en una reducción del universo modificándose en consecuencia la definición.
DETERMINACIÓN DE VARIABLES: Que variables o datos a ser obtenidos es también fundamentalmente una distribución del investigador, pero con frecuencia incluye mas datos de los que realmente necesita para lograr los objetivos y a veces omita otros que son básicos o que son indispensables para el control de las operaciones de campo, y estos son frecuentemente sugeridos por el estadístico; además, que anticipando las asociaciones que se podrían buscar entre dos o más variables es posible que se llegue a la conclusión de que ciertos datos no van a ser utilizados de manera alguna en el análisis y tampoco en las operaciones por lo que su obtención resulta innecesaria.
FORMULACIÓN DE HIPÓTESIS: En el caso en que deba formularse una o hipótesis, el estadístico probablemente no tenga mucho que hacer excepto quizá sugerir el cambiar un poco la redacción de tal manera que quede mas conveniente y expresada para el tipo de análisis que deba hacerse posteriormente.
PROCEDIMIENTO DE MEDICIÓN: aquí deben considerarse las definiciones de las variables, y mientras que el investigador pueda ponerse muy riguroso en relación con la definición de las variables más íntimamente relacionadas con su especialidad, suele descuidar la definición de las otras por considerarlas demasiado evidentes, y la experiencia del estadístico con estas puede ser de gran utilidad.
La medición también es algo que rebase el campo de la estadística; pero mientras que el especialista será el más indicado para establecer cómo se va a decidirla presencia o ausencia de una característica cuya obtención no sea frecuente, será el estadístico el que normalmente está más familiarizado con la forma de medir aquellas otras que se incluyen con mas frecuencia en las investigaciones.
SELECCIÓN DEL DISEÑO: la elección del diseño depende de consideraciones basadas en la información disponible, en la naturaleza de la investigación y en las posibilidades de obtener mayor presición en el análisis estadístico, por lo que la desición sobre el diseño mas adecuado habrá de ser tomada conjuntamente por el investigador y el estadístico.
PROCEDIMIENTO DE CAPTACIÓN: este aspecto cae más naturalmente en la esfera de acción del estadístico. Aquí tampoco debe omitirse la participación del investigador, pues tiene bastante que decir, especialmente acerca de la información que más relación tiene con su especialidad.
PROCEDIMIENTOS DE ELABORACIÓN Y ANÁLISIS: aquí se entra todavía más al campo del estadístico, pero aun aquí la participación del investigador se considera esencial para orientar al estadístico sobre la utilidad de llevar el análisis más allá de donde pudiera haberse anticipado o truncarlo en algún punto por la irrelevancia de los hallazgos.
PROGRAMACIÓN Y CONDUCCIÓN DE LA INVESTIGACIÓN: la participación del estadístico no puede limitarse a contribuir en la elección del diseño, sino que una vez decidida, su realización en la práctica debe ajustarse tanto como sea posible a lo planeado para que el análisis que se proyecta realizar tenga validez. Por lo tanto, el estadístico debe participar activamente en la programación y conducción de la investigación y cualquier modificación que se antoje conveniente no deberá introducirse sin antes haber consultado con él, pues la modificación bien podría invalidar todo el análisis proyectado.
Los datos recogidos deben ser organizados, tabulados, y presentados para su análisis e interpretación sean rápidos y útiles. Por ejemplo, para estudiar e interpretar la distribución de las notas de un examen en una clase con treinta alumnos, primero se ordenan las notas en orden creciente.
Una vez que los datos han sido reunidos y tabulados, comienza el análisis con el objeto de calcular un número único, que represente o resuma todos los datos.
La frecuencia es un numero que nos indica las veces que un dato esta repetido.
La frecuencia acumulada (Fi) es la suma parcial de las frecuencias. La frecuencia Relativa (hi) resulta de dividir la frecuencia fi por el numero total de datos n. La fecuencia absoluta (ni) es la cantidad de veces que aparece un mismo dato en el muetreo. La frecuencia acumulada relativa (Hi) es la suma parcial de las frecuencias relativas.
Para representar visualmente los datos obtenidos en el censo o el muestreo, existen varias formas basicas de graficas estadisticas:
-
HISTOGRAMA: los datos de la variable estadística se representan en el eje horizontal del plano cartesiano, y sus frecuencias absolutas en el eje vertical. Lugo se trazan columnas hasta los puntos del censo.
-
PASTELES: Un circulo o cilindro se divide en sectores proporcionales a los datos del censo o muestreo. Los sectores se indican con su propio valor y/o con porcentajes.
-
POLÍGONO DE FRECUENCIAS: se grafican los puntos del censo como en el caso de los histogramas, y luego se traza una recta o curva que los contenga en su gran mayoria, interponiendolos a través de una función matematica adecuada.
Este método conlleva un estudio mucho mas avanzado en las matemáticas y en la estadística, y su uso es práctico cuando los puntos son muchisimos.
El dicho “una imagen vale más que mil palabras” se puede aplicar al ámbito de la estadística descriptiva afirmando que ``un gráfico bien elaborado vale más que mil tablas de frecuencias''. Cada vez es más habitual el uso de gráficos o imágenes para representar la información obtenida. No obstante, la confección de dichos gráficos debe hacerse con mucho cuidado, y hemos de ser muy prudentes ya que un mínimo error en la representación de una tabla de frecuencia puede cambiar por completo la perspectiva de lo que en realidad desea mostrarse. Se dice que debe hacerse con prudencia porque una misma información puede tener muchas formas de representarse, y no todas son correctas, como debe suponerse.
La estadística juega un papel muy importante en nuestras vidas, ya que actualmente ésta se ha convertido en un método muy efectivo para describir con mucha precisión los valores de datos económicos, políticos, sociales, psicológicos, biológicos y físicos, además, sirve como herramienta para relacionar y analizar dichos datos. El trabajo del experto estadístico ha evolucionado mucho, ya no consiste sólo en reunir y tabular los datos, sino sobre todo en el proceso de interpretación de esa información, ahora tiene un papel mucho más importante del que tenia en años pasados.
Es de vital importancia para nuestra vida profesional venidera, que manejemos estos conceptos con facilidad, así mismo el que los usemos de la manera apropiada, siempre en pro de buscar soluciones a los problemas que se nos puedan presentar.
BIBLIOGRAFÍA
-
Biblioteca de consulta Encarta 2005.
-
Diccionarios Encarta.
-
Matematicas para el nuevo icfes, Los tres editores, 2003.
-
Estadística para las ciencias sociales, Runyon, Richard, Haber, Autrey, Fondo educativo Interamericano, 1992
-
Enciclopedia Norma, matemáticas, Editorial Norma, 1998
-
Analisis financiero Aplicado, Ortiz Anaya, Héctor, universidad externado de Colombia, 1996.
-
Apuntes de Bioestadística, Universidad UDCA Bogotá.
-
Apuntes noveno grado, colegio siervas de san josé
-
Apuntes once grado, colegio Pestalozzi.
-
Apuntes II semestre psicología, universidad IAFIC.
65
CLASES CLASE
50 -59 49.5 - 59.5
50 -59 49.5 - 59.5
50 -59 49.5 - 59.5
50 -59 49.5 - 59.5
50 -59 49.5 - 59.5
50 -59 49.5 - 59.5
4%
16%
24%
36%
14%
6%
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
CLASES (PASAJEROS)
50 60 70 80 90 100 110
49.5 59.5 69.5 79.5 89.5 99.5 109.5
F. absoluta (días)
F. absoluta (días)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
PUNTO MEDIO O MARCA DE CLASE (PASAJEROS)
54.5 64.5 74.5 84.5 94.5 104.5
F. absoluta (días)
1
2
3
4
5
6
7
8
9
10
11
PUNTO MEDIO O MARCA DE CLASE (PASAJEROS)
50 - 59 60 - 69 70 - 79 80 - 89 90 - 99 100 - 109
HOMBRES MUJERES
A B C
90
60
30
A B C
10
20
30
40
50
60
70
80
90
(a)
(b)
Platicúrtica
Mesocúrtica
Leptocúrtica
Bimodal
En U
Rectangular
Positivamente sesgada
Ojiva
En J
Sesgo negativo extremo
50
48
40
28
10
3
CLASES
Menos de 110
Menos de 90
Menos de 100
Menos de 80
Menos de 70
Menos de 60
Menos de 50
Frecuencia acumulada menor de
CLASES
50
47
40
22
10
2
Menos de 110
Menos de 90
Menos de 100
Menos de 80
Menos de 70
Menos de 60
Menos de 50
Frecuencia acumulada mayor de
HOMBRES
MUJERES
NUMERO DE ESTUDIANTES
SEMESTRE…
10
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
2%
26%
26%
18%
34%
14%
FRECUENCIA ABSOLUTA (ESTUDIANTES)
CLASES
2.02
1.94
1.86
1.78
1.70
1.62
1.54
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
FRECUENCIA ABSOLUTA (ESTUDIANTES)
PUNTO MEDIO
1.975
1.895
1.815
1.735
1.655
1.575
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
1.94 - 2.01
1.86 -1.93
1.78 -1.85
1.70 -1.77
1.62 -1.69
9
10
11
12
13
14
HOMBRES
MUJERES
NUMERO DE ESTUDIANTES
CLASE
1.54 -1.61
1
2
3
4
5
6
7
8
46
33
24
7
50
49
F. ACUMULADA MENOR DE
Menos de 2.02
Menos de 1.94
Menos de 1.86
Menos de 1.70
Menos de 1.54
Menos de 1.78
Menos de 1.62
1
47
43
26
17
50
F. ACUMULADA MAYOR DE
2.02 o mas
1.94 o mas
1.86 o mas
1.70 o mas
1.54 o mas
1.78 o mas
1.62 o mas
Descargar
| Enviado por: | Luisa |
| Idioma: | castellano |
| País: | Colombia |



