Estadística
Estadística Aplicada a la Economía
Universidad Nacional De Piura
Estadística Aplicada
Facultad de economía
Piura, Julio del 2005
REGRESIÓN LINEAL BIVARIANTE
REGRESION LINEAL SIMPLE Y ANALISIS DE CORRELACION
OBJETIVOS
-
Utilizar diagramas de dispersión para visualizar la relación entre dos variables.
-
Utilizar el análisis de regresión para estimar la relación entre dos variables.
-
Utilizar la ecuación de regresión para predecir valores futuros.
-
Aplicar el análisis de correlación para describir el grado hasta el cuál dos variables están relacionadas linealmente entre si.
EL DIAGRAMA DE DISPERSIÓN
Es un gráfico que permite detectar la existencia de una relación entre dos variables. Visualmente se puede buscar patrones que indiquen el tipo de relación que se da entre las variables.
RELACIONES POSIBLES ENTRE X e Y
Primer Ejemplo:
TABLA NÚMERO 01: Producto bruto interno y Producto bruto interno
per cápita; 1950 a 1999 (periodicidad anual).
| obs | PBI | PBIPC | obs | PBI | PBIPC | |
| 1950 | 21264 | 2786 | 1975 | 79215 | 5224.9 | |
| 1951 | 23007 | 2939.8 | 1976 | 80800 | 5185.8 | |
| 1952 | 24434 | 3044.5 | 1977 | 81123 | 5066.4 | |
| 1953 | 25729 | 3125.4 | 1978 | 81366 | 4946.5 | |
| 1954 | 27401 | 3243.9 | 1979 | 86086 | 5097.4 | |
| 1955 | 28717 | 3311.6 | 1980 | 90562 | 5227.5 | |
| 1956 | 29951 | 3363.5 | 1981 | 95181 | 5359.6 | |
| 1957 | 31988 | 3497.5 | 1982 | 94610 | 5199.6 | |
| 1958 | 31796 | 3383.8 | 1983 | 83446 | 4478.8 | |
| 1959 | 32973 | 3414.1 | 1984 | 87785 | 4604.6 | |
| 1960 | 36995 | 3725.2 | 1985 | 90243 | 4629.6 | |
| 1961 | 39733 | 3888.7 | 1986 | 99267 | 4984.4 | |
| 1962 | 43071 | 4095.5 | 1987 | 10720 | 5272.1 | |
| 1963 | 44664 | 4125.7 | 1988 | 97881 | 4716.9 | |
| 1964 | 47612 | 4272.6 | 1989 | 86429 | 4084 | |
| 1965 | 49945 | 4355.4 | 1990 | 81983 | 3800.9 | |
| 1966 | 54140 | 4589.6 | 1991 | 83760 | 3813.1 | |
| 1967 | 56198 | 4632.1 | 1992 | 83401 | 3730.8 | |
| 1968 | 56422 | 4522.5 | 1993 | 87375 | 3842.3 | |
| 1969 | 58566 | 4565.1 | 1994 | 98577 | 4261.8 | |
| 1970 | 62022 | 4701.2 | 1995 | 107025 | 4548.1 | |
| 1971 | 64627 | 4763.3 | 1996 | 109263 | 4580.3 | |
| 1972 | 66501 | 4766 | 1997 | 117083 | 4304.2 | |
| 1973 | 70092 | 4885.1 | 1998 | 116595 | 4701.3 | |
| 1974 | 76611 | 5193.6 | 1999 | 118210 | 4684.9 |
FUENTE: Memoria del BCRP - 1999
PBI: Millones de nuevos soles a precios de 1994
PBI per cápita (PBIPC): Nuevos soles a precios de 1994
Donde:
PBI (X): Producto Bruto Interno expresado en millones de nuevos soles
(variable predeterminada)
PBIPC (Y): PBI per cápita expresado en nuevos soles
(variable dependiente, endógena)
TIPO DE RELACIÓN
En este caso los cambios en el PBI (X) provocan cambios en el PBIPC (Y) en igual sentido (aumentos o disminuciones), las variables están directamente relacionadas. Se observa el signo (+)
GRADO DE LA ECUACION
La ecuación es de primer grado, es decir, la variable independiente está elevado al exponente 1. Su gráfica genera una línea recta, por lo que también se le llama ecuación lineal.
GRAFICA DE LA ECUACION
CUADRO NÚMERO 01: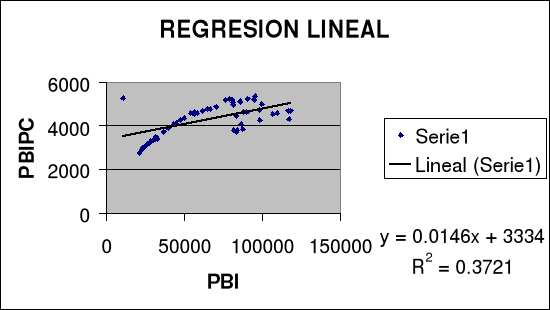
FUENTE: Elaboración propia
FORMA GENERAL
La ecuación simple de primer grado tiene la siguiente forma general
| Y = a + b X |
Donde:
b: Pendiente, o sea, el cambio en Y cuando DX = 1
a: El valor autónomo, es decir, Y = a cuando X = 0
En la gráfica es la intersección con el eje Y
METODO DE MINIMOS CUADRADOS
Es el procedimiento matemático utilizado para determinar los valores numéricos de los coeficientes de regresión a y b.
La ecuación general Y= a + bX se llama ecuación de regresión y permite estimar o predecir los valores de Y.
El método consiste en determinar una ecuación que la suma de los errores al cuadrado sea mínima.
El método utiliza un sistema de ecuación llamado ecuaciones normales, que tienen la siguiente forma:
ESTIMACION MEDIANTE EL MÉTODO DE LOS MÍNIMOS CUADRADOS ORDINARIOS M.C.O
CUADRO NÚMERO 02:
| Dependent Variable: PBIPC | ||||
| Method: Least Squares (Mínimos cuadrados ordinarios) | ||||
| Date: 06/16/97 Time: 11:03 | ||||
| Sample: 1950 1999 (Muestra) | ||||
| Included observations: 50 (Observaciones) | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | 3334.040 | 199.7889 | 16.68782 | 0.0000 |
| PBI | 0.014567 | 0.002731 | 5.333078 | 0.0000 |
| R-squared | 0.372071 | Mean dependent var | 4310.750 | |
| Adjusted R-squared | 0.358989 | S.D. dependent var | 705.1481 | |
| S.E. of regression | 564.5640 | F-statistic | 28.44172 | |
| Sum squared resid | 15299159 | Prob(F-statistic) | 0.000003 | |
FUENTE: Elaboración propia
COEFICIENTE DE DETERMINACION
| R² = 0.3721 |
El 37.21% de las variaciones en el PBI per cápita pueden explicarse a través del PBI nacional.
ESTADISTICAS DESCRIPTIVAS
CUADRO NÚMERO 03: HISTOGRAMA PBI
FUENTE: Elaboración propia
CUADRO NÚMERO 04: HISTOGRAMA PBIPC
FUENTE: Elaboración propia
PRUEBAS DE SIGNIFICANCIA ESTADISTICA
Sea el modelo bivariado:
| PBIPC = |
Donde:
u: Variable estocástica
BONDAD DE AJUSTE (R-squared = 0.372071)
Solo el 37.21 % de los cambios en el PBIPC son explicados en conjunto por la variable PBI.
ANALISIS DE SERIES DE TIEMPO
Para todo análisis de series de tiempo existen cuatro componentes:
-
Componente cíclico
-
Componente tendencial
-
Componente estacional
-
Componete irregular
COMPONENTE TENDENCIAL
Es la tendencia de toda serie a largo plazo sin sufrir alteraciones.
CUADRO NÚMERO 05: Analisis tendencial del PBI 1950-1999
FUENTE: Elaboración propia
A través del gráfico podemos observar que la tendencia secular del PBI a lo largo de las décadas de los 50s, 60s, 70s y principios de los 80s es creciente. A partir del año 85 se observa una drástica caída del mismo debido a cambios estructurales en la política macroeconómica del país (existía un mayor poder de compra). Hasta ese año (1985) se pasó de una política de minidevaluaciones (Gobierno de Belaunde) a una política cambiaraia fija (Gobierno de Alan García).
COMPONENTE CICLICO
Es el ascenso y el descenso de una serie en períodos mayores de un año. Es un componente de corto plazo, mayormente de coyuntura.
CUADRO NÚMERO 06: Analisis cíclico del PBICP 1950-1999
FUENTE: Elaboración propia
La tendencia cíclica del PBIPC de 1950-1999 resalta períodos de recuperación y períodos de recesión, es decir ascenso y descenso del PBIPC.
COMPONENTE ESTACIONAL
La data presentada no especifica adecuadamente un patrón o esquema de cambio al año. Para que exista el componente estacional tales patrones tienen que repetirse cada año. En tal efecto, no existe variación estacional debido a que los datos se registran anualmente.
COMPONENTE IRREGULAR
Es la variabilidad de la serie debido a hechos exógenos, aleatorios, como guerras, fenómenos climatológicos, etc.
CUADRO NÚMERO 07: Analisis irregular del PBI 1980-1990
FUENTE: Elaboración propia
El análisis irregular del PBI 1980 - 1990 nos muestra un período de descenso en la economía nacional. En el año 1983 el fenómemno climatológico del niño obligó a un descenso en la economía nacional (hecho exógeno, irregular). Ver gráfico año 1983.
TENDENCIAS
Tendencias Lineales
Es aquella serie de tiempo cuyo crecimiento o decrecimiento se aproxima a una línea recta, y tiene la siguiente forma:
| Y = a + b X |
CUADRO NÚMERO 08: Estimación por mínimos cuadrados ordinarios
| Dependent Variable: PBIPC | ||||
| Method: Least Squares (Regresión Lineal) | ||||
| Date: 06/21/97 Time: 02:52 | ||||
| Sample: 1950 1999 (MUESTRA) | ||||
| Included observations: 50 | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | 3334.040 | 199.7889 | 16.68782 | 0.0000 |
| PBI | 0.014567 | 0.002731 | 5.333078 | 0.0000 |
| R-squared | 0.372071 | Mean dependent var | 4310.750 | |
| Adjusted R-squared | 0.358989 | S.D. dependent var | 705.1481 | |
| S.E. of regression | 564.5640 | Akaike info criterion | 15.54916 | |
| Sum squared resid | 15299159 | Schwarz criterion | 15.62564 | |
| Log likelihood | -386.7291 | F-statistic | 28.44172 | |
| Durbin-Watson stat | 0.472083 | Prob(F-statistic) | 0.000003 | |
FUENTE: Elaboración propia
CUADRO NÚMERO 09:
FUENTE: Elaboración propia
PRONOSTICO Y PREDICCION
Una de las formas de realizar una adecuada predicción es verificando la tendencia del comportamiento de las variables a lo largo del tiempo, es decir, conocer las tendencias de las variables. Esto se puede realizar mediante diagramas de tendencia, como el siguiente:
CUADRO NÚMERO 10:
FUENTE: Elaboración propia
La línea del medio nos muestra que la tendencia del PBIPC en el futuro es ascendente, y no muestra signos de inestabilidad paramétrica, puesto que se encuentra entre las dos líneas de rangos.
Algo muy importante de resaltar es que si el coeficiente theil inequality coefficient (ver reporte) se acerca acero, entonces la predicción es adecuada.
Tendencias no Lineales
Ecuación de tendencia logarítmica - logaritmo Neperiano (Ln)
Esta se puede calcular usando los logaritmos de la data y aplicando el método de los mínimos cuadrados ordinarios. Su ecuación general será:
| ln Y = ln a + ln b (X) |
ESTIMACION
CUADRO NÚMERO 11:
| Dependent Variable: LOG(PBIPC) | ||||
| Method: Least Squares | ||||
| Date: 06/21/97 Time: 02:12 | ||||
| Sample: 1950 1999 (MUESTRA) | ||||
| Included observations: 50 | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | 6.172560 | 0.388278 | 15.89726 | 0.0000 |
| LOG(PBI) | 0.198601 | 0.035295 | 5.626886 | 0.0000 |
| R-squared | 0.397453 | Mean dependent var | 8.354658 | |
| Adjusted R-squared | 0.384900 | S.D. dependent var | 0.173963 | |
| S.E. of regression | 0.136437 | Akaike info criterion | -1.106736 | |
| Sum squared resid | 0.893517 | Schwarz criterion | -1.030256 | |
| Log likelihood | 29.66841 | F-statistic | 31.66185 | |
| Durbin-Watson stat | 0.705365 | Prob(F-statistic) | 0.000001 | |
FUENTE: Elaboración propia
CUADRO NÚMERO 12:
FUENTE: Elaboración propia
ESTABILIDAD
COMPROBACION DE ESTABILIDAD A TRAVES
DEL TIEMPO
Este tipo de estimación me permite detectar cambios estructurales en la economía, mencionados anteriormente. De acuerdo a este test voy a comprobar si hay estabilida o no.
El análisis es simple (aunque no lo paresca), si la línea de tendencia (la que está en medio de ambas líneas) no sale del rango, significa que hay estabilidad paramétrica.
En este caso el PBI y el PBIPC, se han mantenido estables a lo largo del tiempo, aún así esta prueba no es determinística.
VARIACION ESTACIONAL
No existe variación estacional puesto que los datos tienen periodicidad anual, es decir, se registran anualmente.
NUMEROS INDICES
Número Indice
Es un número que expresa un cambio relativo de un lapso de tiempo a otro, en los conceptos de precio, cantidad o valor.
Si el número índice se usa para medir el cambio relativo en solo una variable - como el salario por hora en un proceso de fabricación - se le denomina índice simple. Es la razón o relación proporcional entre dos variables expresada como porcentaje.
Segundo Ejemplo:
CANTIDAD TRANSADA DE CARNE
Periodicidad: Mensual
01: Enero 05: Mayo 09: Septiembre
02: Febrero 06: Junio 10: Octubre
03: Marzo 07: Julio 11: Noviembre
04: Abril 08: Agosto 12: Diciembre
TABLA NÚMERO 02: Cantidad transada de carne.
| obs | QV | PCV | PCC | Y |
| 1994:01:00 | 922240 | 1.11 | 1.31 | 132.7 |
| 1994:02:00 | 831350 | 1.23 | 1.27 | 130.6 |
| 1994:03:00 | 100376 | 1.24 | 1.26 | 177.7 |
| 1994:04:00 | 114883 | 1.2 | 1.33 | 189.1 |
| 1994:05:00 | 112386 | 1.22 | 1.32 | 187.9 |
| 1994:06:00 | 113365 | 1.24 | 1.35 | 185.8 |
| 1994:07:00 | 123906 | 1.25 | 1.41 | 227.1 |
| 1994:08:00 | 120399 | 1.27 | 1.37 | 223.7 |
| 1994:09:00 | 113701 | 1.25 | 1.35 | 227.6 |
| 1994:10:00 | 122619 | 1.24 | 1.36 | 261 |
| 1994:11:00 | 131527 | 1.24 | 1.4 | 257.9 |
| 1994:12:00 | 122635 | 1.28 | 1.42 | 256.4 |
| 1995:01:00 | 141777 | 1.27 | 1.44 | 255.4 |
| 1995:02:00 | 120074 | 1.28 | 1.45 | 252.5 |
| 1995:03:00 | 145071 | 1.28 | 1.44 | 249.1 |
| 1995:04:00 | 136150 | 1.27 | 1.42 | 246.7 |
| 1995:05:00 | 139859 | 1.26 | 1.43 | 244.7 |
| 1995:06:00 | 150236 | 1.26 | 1.44 | 242.7 |
| 1995:07:00 | 154736 | 1.25 | 1.43 | 241.3 |
| 1995:08:00 | 146548 | 1.24 | 1.42 | 238.8 |
| 1995:09:00 | 139779 | 1.24 | 1.46 | 237.9 |
| 1995:10:00 | 134202 | 1.23 | 1.49 | 236.7 |
| 1995:11:00 | 124587 | 1.22 | 1.47 | 233.8 |
| 1995:12:00 | 142109 | 1.21 | 1.47 | 232.6 |
| 1996:01:00 | 155005 | 1.21 | 1.46 | 260.8 |
| 1996:02:00 | 144071 | 1.21 | 1.46 | 262.9 |
| 1996:03:00 | 146337 | 1.2 | 1.41 | 264.9 |
| 1996:04:00 | 138297 | 1.19 | 1.39 | 266.6 |
| 1996:05:00 | 138908 | 1.21 | 1.4 | 268.1 |
| 1996:06:00 | 128889 | 1.22 | 1.38 | 262.3 |
| 1996:07:00 | 159663 | 1.2 | 1.36 | 270.4 |
| 1996:08:00 | 173068 | 1.19 | 1.37 | 271.2 |
| 1996:09:00 | 158662 | 1.18 | 1.39 | 271.7 |
| 1996:10:00 | 154556 | 1.17 | 1.39 | 272 |
| 1996:11:00 | 177353 | 1.17 | 1.4 | 272.1 |
| 1996:12:00 | 131177 | 1.16 | 1.38 | 271.8 |
FUENTE: Gobierno Regional de Piura
Donde:
QV : Cantidad transada de carne de vacuno mensual en kg
PCV : Precio de la carne de vacuno, expresada en soles por kg
PCC : Precio de la carne de cordero, expresado en soles por kg
Y : Ingreso mensual familiar
OBTENCION DE LOS NUMEROS INDICES A TRAVES DE EXEL
INDICE SIMPLE
Es el cambio relativo en una sola variable:
P = ( pt/p0 ) * 100
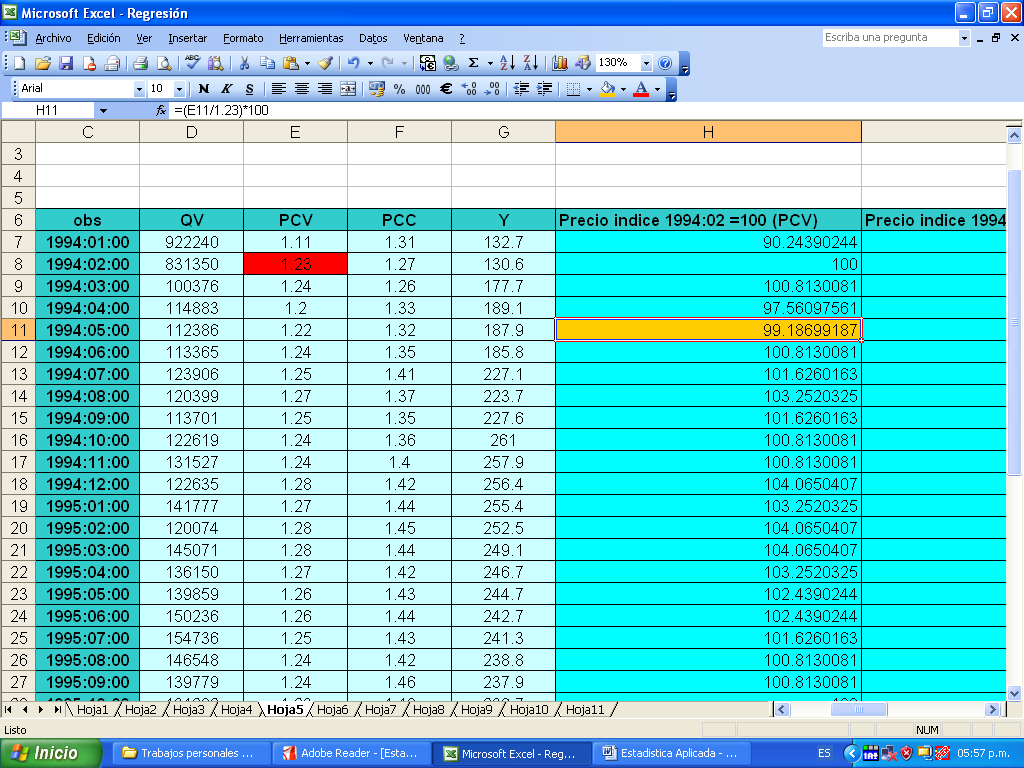
El siguiente ejemplo nos muestra la obtención del indice simple del precio de la carne de vacuno, tomando primero como año base, 1994 - mes de febrero (02), para después tomar como año base, el mismo año (1994) pero en los meses de Febrero y Marzo, es decir, como la periodicidad es mensual, estoy tomando dos periodos bases (Febrero y Marzo):
TABLA NÚMERO 03: Cantidad transada de carne.
| obs | PCV | Precio índice 1994:02 =100 | Precio índice 1994:02 - 03=100 |
| 1994:01:00 | 1.11 | 90.24390244 | 89.87854251 |
| 1994:02:00 | 1.23 | 100 | 99.5951417 |
| 1994:03:00 | 1.24 | 100.8130081 | 100.4048583 |
| 1994:04:00 | 1.2 | 97.56097561 | 97.1659919 |
| 1994:05:00 | 1.22 | 99.18699187 | 98.7854251 |
| 1994:06:00 | 1.24 | 100.8130081 | 100.4048583 |
| 1994:07:00 | 1.25 | 101.6260163 | 101.2145749 |
| 1994:08:00 | 1.27 | 103.2520325 | 102.8340081 |
| 1994:09:00 | 1.25 | 101.6260163 | 101.2145749 |
| 1994:10:00 | 1.24 | 100.8130081 | 100.4048583 |
| 1994:11:00 | 1.24 | 100.8130081 | 100.4048583 |
| 1994:12:00 | 1.28 | 104.0650407 | 103.6437247 |
| 1995:01:00 | 1.27 | 103.2520325 | 102.8340081 |
| 1995:02:00 | 1.28 | 104.0650407 | 103.6437247 |
| 1995:03:00 | 1.28 | 104.0650407 | 103.6437247 |
| 1995:04:00 | 1.27 | 103.2520325 | 102.8340081 |
| 1995:05:00 | 1.26 | 102.4390244 | 102.0242915 |
| 1995:06:00 | 1.26 | 102.4390244 | 102.0242915 |
| 1995:07:00 | 1.25 | 101.6260163 | 101.2145749 |
| 1995:08:00 | 1.24 | 100.8130081 | 100.4048583 |
| 1995:09:00 | 1.24 | 100.8130081 | 100.4048583 |
| 1995:10:00 | 1.23 | 100 | 99.5951417 |
| 1995:11:00 | 1.22 | 99.18699187 | 98.7854251 |
| 1995:12:00 | 1.21 | 98.37398374 | 97.9757085 |
| 1996:01:00 | 1.21 | 98.37398374 | 97.9757085 |
| 1996:02:00 | 1.21 | 98.37398374 | 97.9757085 |
| 1996:03:00 | 1.2 | 97.56097561 | 97.1659919 |
| 1996:04:00 | 1.19 | 96.74796748 | 96.3562753 |
| 1996:05:00 | 1.21 | 98.37398374 | 97.9757085 |
| 1996:06:00 | 1.22 | 99.18699187 | 98.7854251 |
| 1996:07:00 | 1.2 | 97.56097561 | 97.1659919 |
| 1996:08:00 | 1.19 | 96.74796748 | 96.3562753 |
| 1996:09:00 | 1.18 | 95.93495935 | 95.5465587 |
| 1996:10:00 | 1.17 | 95.12195122 | 94.73684211 |
| 1996:11:00 | 1.17 | 95.12195122 | 94.73684211 |
| 1996:12:00 | 1.16 | 94.30894309 | 93.92712551 |
FUENTE: Gobierno Regional de Piura
INDICES NO PONDERADOS
PROMEDIO SIMPLE DE PRECIOS RELATIVOS
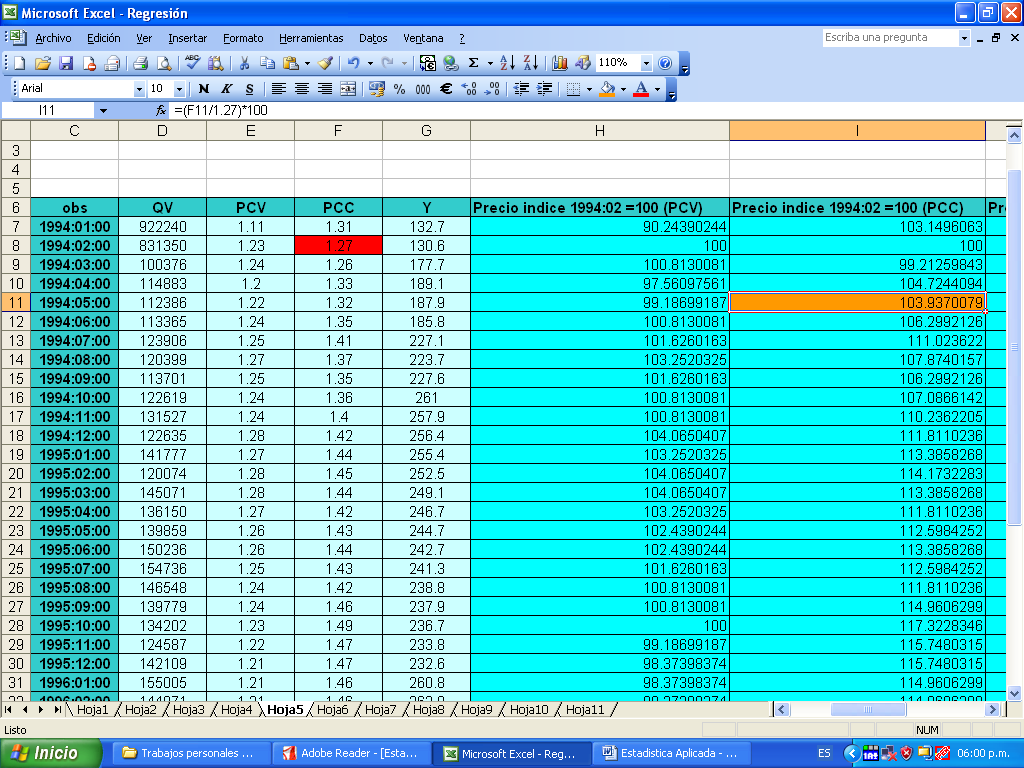
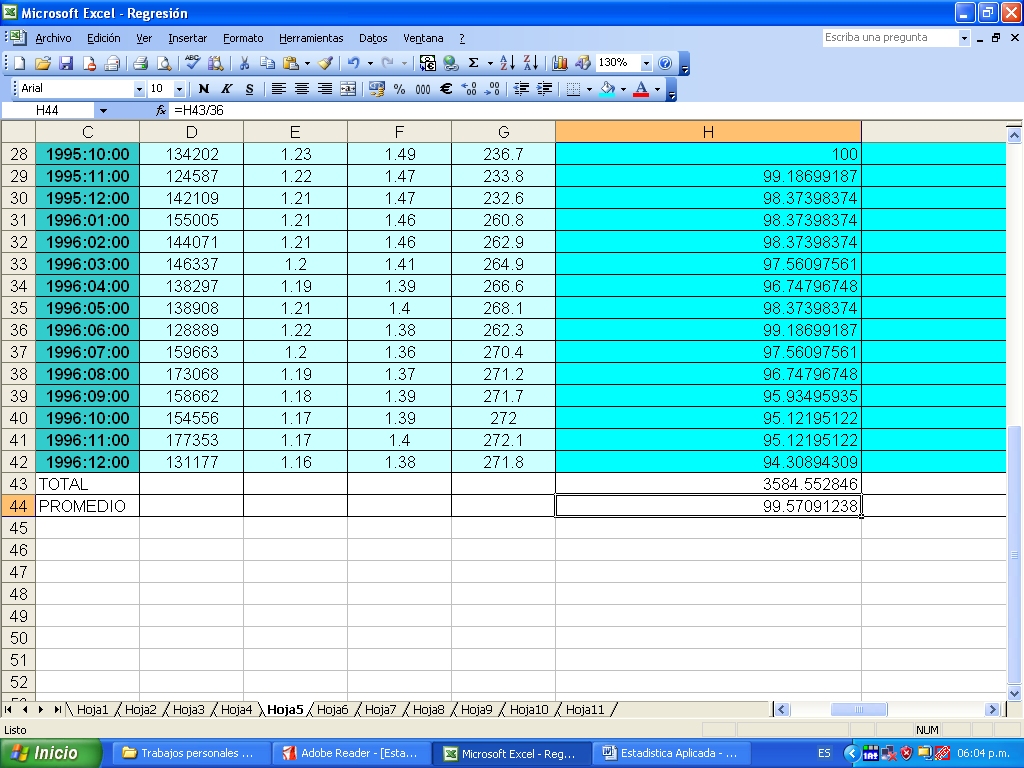
Hallamos el promedio simple de precios relativos para la carne vacuno y de cordero respectivamente (1994:02 = 100):
P = (sum pi/n)
TABLA NÚMERO 04: Cantidad transada de carne.
| obs | PCV | PCC | Precio indice 1994:02 =100 (PCV) | Precio indice 1994:02 =100 (PCC) |
| 1994:01:00 | 1.11 | 1.31 | 90.24390244 | 103.1496063 |
| 1994:02:00 | 1.23 | 1.27 | 100 | 100 |
| 1994:03:00 | 1.24 | 1.26 | 100.8130081 | 99.21259843 |
| 1994:04:00 | 1.2 | 1.33 | 97.56097561 | 104.7244094 |
| 1994:05:00 | 1.22 | 1.32 | 99.18699187 | 103.9370079 |
| 1994:06:00 | 1.24 | 1.35 | 100.8130081 | 106.2992126 |
| 1994:07:00 | 1.25 | 1.41 | 101.6260163 | 111.023622 |
| 1994:08:00 | 1.27 | 1.37 | 103.2520325 | 107.8740157 |
| 1994:09:00 | 1.25 | 1.35 | 101.6260163 | 106.2992126 |
| 1994:10:00 | 1.24 | 1.36 | 100.8130081 | 107.0866142 |
| 1994:11:00 | 1.24 | 1.4 | 100.8130081 | 110.2362205 |
| 1994:12:00 | 1.28 | 1.42 | 104.0650407 | 111.8110236 |
| 1995:01:00 | 1.27 | 1.44 | 103.2520325 | 113.3858268 |
| 1995:02:00 | 1.28 | 1.45 | 104.0650407 | 114.1732283 |
| 1995:03:00 | 1.28 | 1.44 | 104.0650407 | 113.3858268 |
| 1995:04:00 | 1.27 | 1.42 | 103.2520325 | 111.8110236 |
| 1995:05:00 | 1.26 | 1.43 | 102.4390244 | 112.5984252 |
| 1995:06:00 | 1.26 | 1.44 | 102.4390244 | 113.3858268 |
| 1995:07:00 | 1.25 | 1.43 | 101.6260163 | 112.5984252 |
| 1995:08:00 | 1.24 | 1.42 | 100.8130081 | 111.8110236 |
| 1995:09:00 | 1.24 | 1.46 | 100.8130081 | 114.9606299 |
| 1995:10:00 | 1.23 | 1.49 | 100 | 117.3228346 |
| 1995:11:00 | 1.22 | 1.47 | 99.18699187 | 115.7480315 |
| 1995:12:00 | 1.21 | 1.47 | 98.37398374 | 115.7480315 |
| 1996:01:00 | 1.21 | 1.46 | 98.37398374 | 114.9606299 |
| 1996:02:00 | 1.21 | 1.46 | 98.37398374 | 114.9606299 |
| 1996:03:00 | 1.2 | 1.41 | 97.56097561 | 111.023622 |
| 1996:04:00 | 1.19 | 1.39 | 96.74796748 | 109.4488189 |
| 1996:05:00 | 1.21 | 1.4 | 98.37398374 | 110.2362205 |
| 1996:06:00 | 1.22 | 1.38 | 99.18699187 | 108.6614173 |
| 1996:07:00 | 1.2 | 1.36 | 97.56097561 | 107.0866142 |
| 1996:08:00 | 1.19 | 1.37 | 96.74796748 | 107.8740157 |
| 1996:09:00 | 1.18 | 1.39 | 95.93495935 | 109.4488189 |
| 1996:10:00 | 1.17 | 1.39 | 95.12195122 | 109.4488189 |
| 1996:11:00 | 1.17 | 1.4 | 95.12195122 | 110.2362205 |
| 1996:12:00 | 1.16 | 1.38 | 94.30894309 | 108.6614173 |
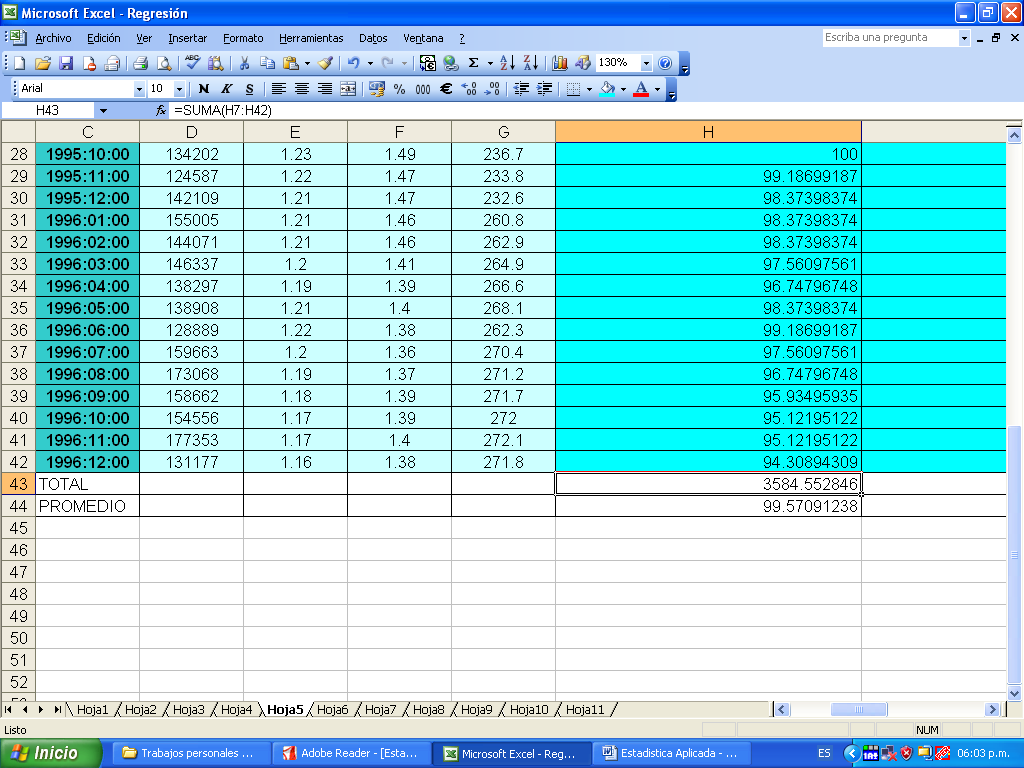
| TOTAL | 3584.552846 | 3960.629921 | ||
| PROMEDIO SIMPLE | 99.57091238 | 110.0174978 |
FUENTE: Elaboración propia
INDICE AGREGADO SIMPLE
P = (sum pt/sum p0) * 100
TABLA NÚMERO 05: Cantidad transada de carne.
| 1994:10 = 100 | PRECIO 1994:10 | PRECIO 1996:12 |
| CARNE DE VACUNO | 1.24 | 1.16 |
| CARNE DE CORDERO | 1.36 | 1.38 |
| TOTAL | 2.6 | 2.54 |
| INDICE AGREGADO SIMPLE | 97.69230769 |
FUENTE: Elaboración propia
INDICES PONDERADOS
Existen dos métodos para calcular un índice de precios ponderado:
-
El índice de Laspeyres
-
El índice de Paasche
Ambos difieren sólo con respecto al período utilizado para la ponderación, veamos:
INDICE DE PRECIOS DE LASPEYRES
El método de Laspeyres emplea ponderaciones de período base, es decir, los precios y las cantidades originales de los artículos comprados se utilizan para hallar el cambio porcentual respecto a un período o intervalo de tiempo, en precio o cantidad consumida, dependiendo de ello el problema, veamos:
P = (sum ptq0/sum p0q0) * 100
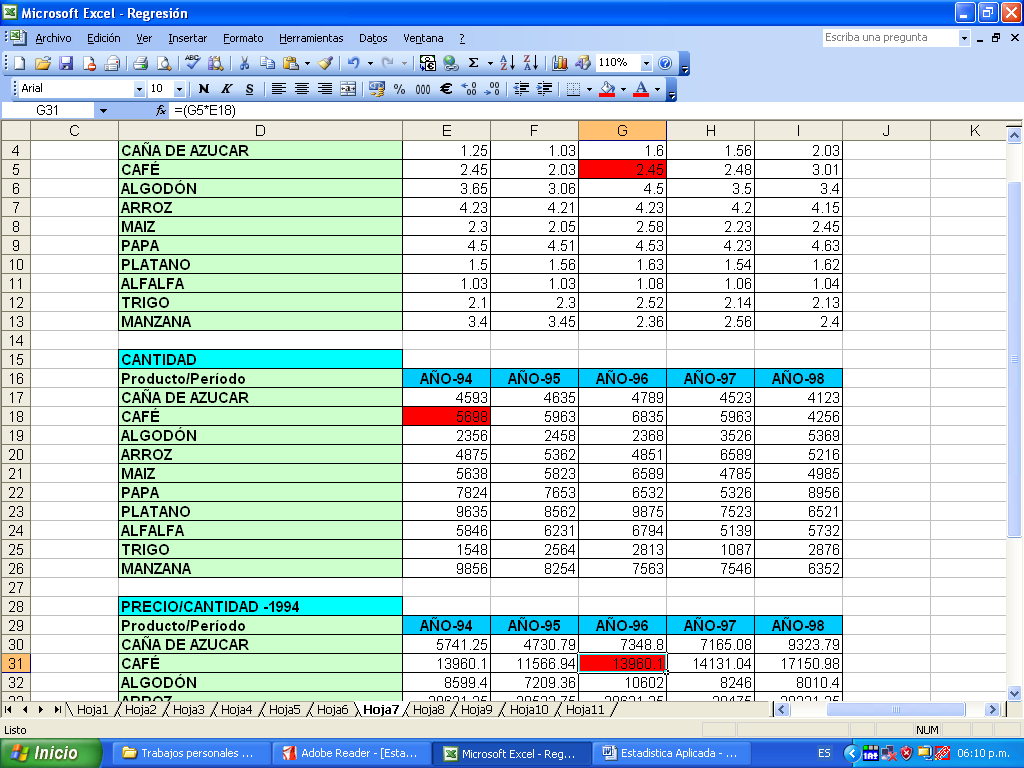
TABLA NÚMERO 06: Precios de productos exportables.
| PRECIO | |||||
| Producto/Período | AÑO-94 | AÑO-95 | AÑO-96 | AÑO-97 | AÑO-98 |
| CAÑA DE AZUCAR | 1.25 | 1.03 | 1.6 | 1.56 | 2.03 |
| CAFÉ | 2.45 | 2.03 | 2.45 | 2.48 | 3.01 |
| ALGODÓN | 3.65 | 3.06 | 4.5 | 3.5 | 3.4 |
| ARROZ | 4.23 | 4.21 | 4.23 | 4.2 | 4.15 |
| MAIZ | 2.3 | 2.05 | 2.58 | 2.23 | 2.45 |
| PAPA | 4.5 | 4.51 | 4.53 | 4.23 | 4.63 |
| PLATANO | 1.5 | 1.56 | 1.63 | 1.54 | 1.62 |
| ALFALFA | 1.03 | 1.03 | 1.08 | 1.06 | 1.04 |
| TRIGO | 2.1 | 2.3 | 2.52 | 2.14 | 2.13 |
| MANZANA | 3.4 | 3.45 | 2.36 | 2.56 | 2.4 |
FUENTE: Gobierno Regional de Piura
TABLA NÚMERO 07: Precios de productos exportables.
| CANTIDAD | |||||
| Producto/Período | AÑO-94 | AÑO-95 | AÑO-96 | AÑO-97 | AÑO-98 |
| CAÑA DE AZUCAR | 4593 | 4635 | 4789 | 4523 | 4123 |
| CAFÉ | 5698 | 5963 | 6835 | 5963 | 4256 |
| ALGODÓN | 2356 | 2458 | 2368 | 3526 | 5369 |
| ARROZ | 4875 | 5362 | 4851 | 6589 | 5216 |
| MAIZ | 5638 | 5823 | 6589 | 4785 | 4985 |
| PAPA | 7824 | 7653 | 6532 | 5326 | 8956 |
| PLATANO | 9635 | 8562 | 9875 | 7523 | 6521 |
| ALFALFA | 5846 | 6231 | 6794 | 5139 | 5732 |
| TRIGO | 1548 | 2564 | 2813 | 1087 | 2876 |
| MANZANA | 9856 | 8254 | 7563 | 7546 | 6352 |
FUENTE: Gobierno Regional de Piura
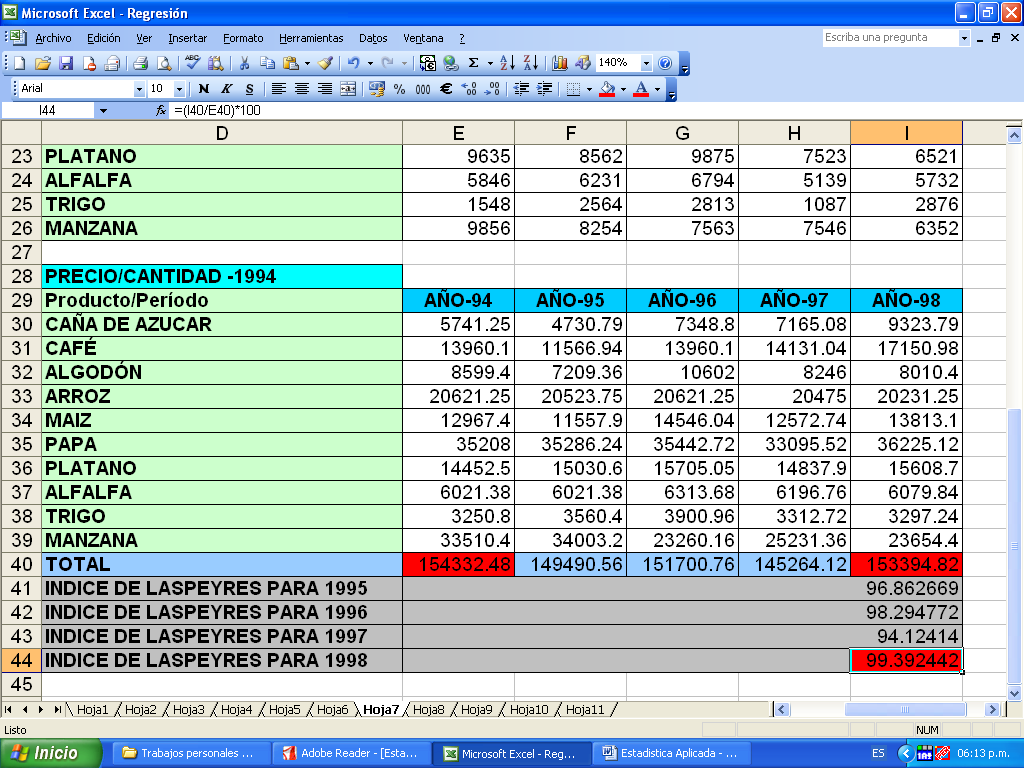
TABLA NÚMERO 08: Precios de productos exportables.
| PRECIO/CANTIDAD (1994=100) | AÑO-94 | AÑO-95 | AÑO-96 | AÑO-97 | AÑO-98 |
| CAÑA DE AZUCAR | 5741.25 | 4730.79 | 7348.8 | 7165.08 | 9323.79 |
| CAFÉ | 13960.1 | 11566.94 | 13960.1 | 14131.04 | 17150.98 |
| ALGODÓN | 8599.4 | 7209.36 | 10602 | 8246 | 8010.4 |
| ARROZ | 20621.25 | 20523.75 | 20621.25 | 20475 | 20231.25 |
| MAIZ | 12967.4 | 11557.9 | 14546.04 | 12572.74 | 13813.1 |
| PAPA | 35208 | 35286.24 | 35442.72 | 33095.52 | 36225.12 |
| PLATANO | 14452.5 | 15030.6 | 15705.05 | 14837.9 | 15608.7 |
| ALFALFA | 6021.38 | 6021.38 | 6313.68 | 6196.76 | 6079.84 |
| TRIGO | 3250.8 | 3560.4 | 3900.96 | 3312.72 | 3297.24 |
| MANZANA | 33510.4 | 34003.2 | 23260.16 | 25231.36 | 23654.4 |
| TOTAL | 154332.48 | 149490.56 | 151700.76 | 145264.12 | 153394.82 |
| INDICE DE LASPEYRES PARA 1995 | 96.86266948 | ||||
| INDICE DE LASPEYRES PARA 1996 | 98.29477243 | ||||
| INDICE DE LASPEYRES PARA 1997 | 94.1241403 | ||||
| INDICE DE LASPEYRES PARA 1998 | 99.39244157 |
FUENTE: Elaboración propia
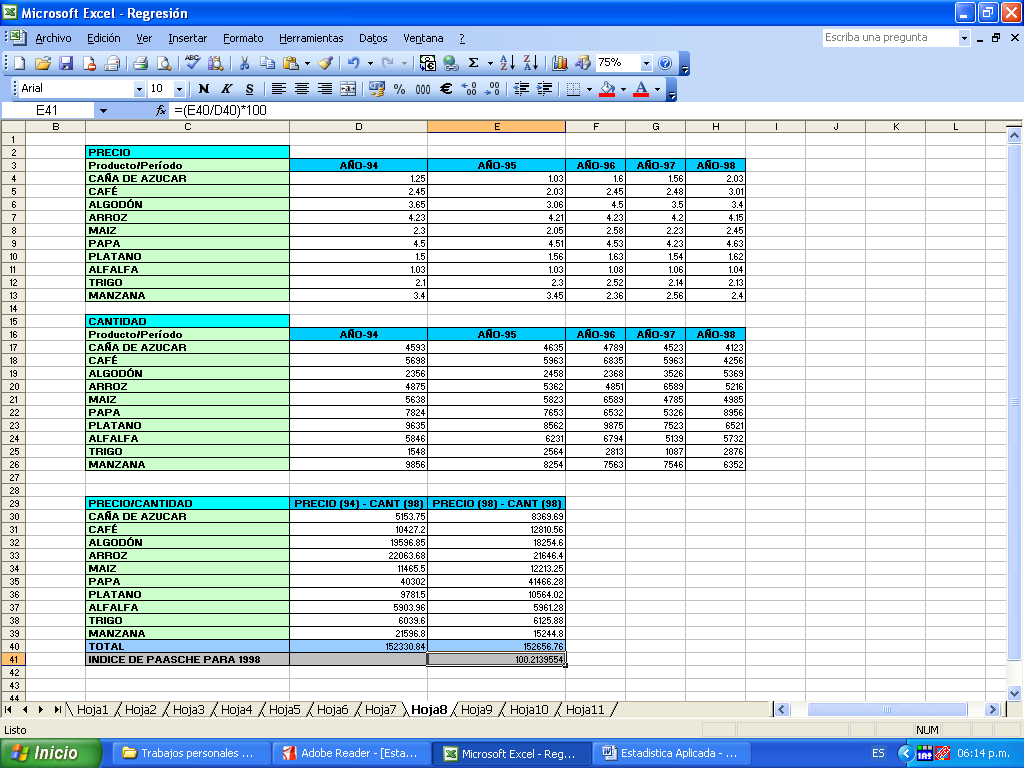
INDICE DEPRECIOS DE PAASCHE
Este método utiliza ponderaciones del año actual para el denominador del índice ponderado:
P = (sum ptqt/sum p0qt) * 100
TABLA NÚMERO 09: Precios de productos exportables.
| PRECIO/CANTIDAD (1994 =100) | PRECIO (94) - CANT (98) | PRECIO (98) - CANT (98) |
| CAÑA DE AZUCAR | 5153.75 | 8369.69 |
| CAFÉ | 10427.2 | 12810.56 |
| ALGODÓN | 19596.85 | 18254.6 |
| ARROZ | 22063.68 | 21646.4 |
| MAIZ | 11465.5 | 12213.25 |
| PAPA | 40302 | 41466.28 |
| PLATANO | 9781.5 | 10564.02 |
| ALFALFA | 5903.96 | 5961.28 |
| TRIGO | 6039.6 | 6125.88 |
| MANZANA | 21596.8 | 15244.8 |
| TOTAL | 152330.84 | 152656.76 |
| INDICE DE PAASCHE PARA 1998 | 100.2139554 |
FUENTE: Elaboración propia
INDICE IDEAL DE FISHER
Combina las mejores características de Laspeyres y Paasche:
Indice ideal de Fisher = sqr((Laspeyres)( Paasche))
| INDICE IDEAL DE FISHER PARA 1998 | 99.80235321 |
INDICE DE VALOR
Un ídice de valor mide cambios tanto en los precios, como en las cantidades que intervienen:
V = (sum ptqt/sum p0q0) * 100
TABLA NÚMERO 10: Precios de productos exportables.
| PRECIO/CANTIDAD (1994 = 100) | AÑO-94 | AÑO-95 | AÑO-96 | AÑO-97 | AÑO-98 |
| CAÑA DE AZUCAR | 5741.25 | 4774.05 | 7662.4 | 7055.88 | 8369.69 |
| CAFÉ | 13960.1 | 12104.89 | 16745.75 | 14788.24 | 12810.56 |
| ALGODÓN | 8599.4 | 7521.48 | 10656 | 12341 | 18254.6 |
| ARROZ | 20621.3 | 22574.02 | 20519.73 | 27673.8 | 21646.4 |
| MAIZ | 12967.4 | 11937.15 | 16999.62 | 10670.55 | 12213.25 |
| PAPA | 35208 | 34515.03 | 29589.96 | 22528.98 | 41466.28 |
| PLATANO | 14452.5 | 13356.72 | 16096.25 | 11585.42 | 10564.02 |
| ALFALFA | 6021.38 | 6417.93 | 7337.52 | 5447.34 | 5961.28 |
| TRIGO | 3250.8 | 5897.2 | 7088.76 | 2326.18 | 6125.88 |
| MANZANA | 33510.4 | 28476.3 | 17848.68 | 19317.76 | 15244.8 |
| TOTAL | 154332 | 147574.8 | 150544.7 | 133735.2 | 152656.8 |
| INDICE DE VALOR PARA 1995 (1994 = 100) | 95.62133 | ||||
| INDICE DE VALOR PARA 1996 (1994 = 100) | 97.54568 | ||||
| INDICE DE VALOR PARA 1997 (1994 = 100) | 86.65392 | ||||
| INDICE DE VALOR PARA 1998 (1994 = 100) | 98.91421 |
FUENTE: Elaboración propia
OTROS INDICES
Ibovespa: Índice representativo del mercado de bursátil de San Pablo, Brasil. Es una cartera teórica compuesto por las acciones que representaron el 80% del volumen negociado durante los últimos 12 meses. La composición del índice es revisada cuatrimestralmente.
Merval: Índice representativo del mercado de bursátil de Buenos Aires, Argentina. Es una cartera teórica compuesto por las acciones que representaron el 80% del volumen negociado durante los últimos 6 meses. La composición del índice es revisada trimestralmente.
Lima General: Índice General de la Bolsa de Valores de Lima (IGBVL), Perú. Refleja la tendencia promedio de las cotizaciones de las principales acciones inscritas en la Bolsa, en función de una cartera seleccionada, que actualmente representa a las 29 acciones más negociadas del mercado. Su cálculo considera las variaciones de precios y los dividendos o acciones liberadas repartidas, así como la suscripción de acciones. Tiene como fecha base 30 de diciembre de 1991 = 100.
IPSA: El IPSA es el Indice de Precios Selectivo de Acciones de la Bolsa de Chile, que mide las variaciones de precios de las 40 sociedades con mayor presencia bursátil (son las acciones con mayor liquidez o flujo en el mercado).
IPC: El Índice de Precios y Cotizaciones es el principal indicador de la Bolsa Mexicana de Valores, expresa el rendimiento del mercado accionario, en función de las variaciones de precios de una muestra balanceada, ponderada y representativa del conjunto de acciones cotizadas en la Bolsa. El tamaño de la muestra es actualmente de 36 acciones (ha oscilado entre 35 y 50). Este indicador, aplicado en su actual estructura desde 1978, expresa en forma fidedigna la situación del mercado bursátil y su dinamismo operativo.
IBC: El Indice Bursátil Caracas (IBC) es el promedio aritmético de la capitalización de los 15 títulos de mayor liquidez del mercado accionario de la Bolsa de Valores de Caracas, Venezuela. El nivel del índice equivale a la suma de las capitalizaciones de todas los acciones incluidas en una canasta. El precio de cada acción es su capitalización de mercado (número de acciones multiplicado por el precio). De esta forma, los movimientos de precio de los títulos más grandes originan grandes movimientos en el índice.
Ibex-35: Índice oficial de la Bolsa de España compuesto por los 35 valores más líquidos y de mayor capitalización.
Nikkei 225: Índice de la Bolsa de Tokio. Su nombre procede del mayor diario económico del mundo, el "Nihon Keizai Shimbun". El índice Nikkey 225 incluye las 225 mayores empresas japonesas, cotizadas en el primer mercado de la Bolsa de Tokio. El Nikkey se publicó por primera vez el 16 de mayo de 1949.
S&P 500: El S&P 500 es el índice más seguido para tener una idea del desempeño general de las acciones estadounidenses. Este índice consiste de las acciones de 500 empresas que fueron seleccionadas por su tamaño, liquidez (qué tan fácil es comprar o vender sus títulos) y representatividad por actividad económica, incluyendo 400 industriales, 20 del sector transporte, 40 de servicios y 40 financieras. Sólo se toman en cuenta empresas estadounidenses. Vale la pena destacar que el peso de cada acción dentro del índice corresponde a la proporción que representa el valor de mercado de la empresa dentro del total de las 500 empresas que conforman el índice. El valor de mercado del capital es igual al precio por acción multiplicado por el número total de acciones.
Dow Jones Industrials Average (DJIA): Es un índice bursátil. Representa la variación de 30 compañías industriales de Estados Unidos. Como cualquier otro, su objetivo es medir la variación promedio de un grupo de acciones para dar a los inversionistas una idea de la evolución de un cierto mercado o sector. En el caso particular del DJIA, se trata de las principales empresas estadounidenses (empresas grandes y conocidas). Es diferente a la mayoría de los índices en la medida en que sus integrantes son elegidos sin un criterio muy preciso y, además, el peso que se le asigna a cada acción tiene que ver con su precio (normalmente, el peso de una empresa dentro de un índice depende del valor de su capital). Así, en realidad es muy poco representativo de los mercados estadounidenses. Sin embargo, es muy seguido y citado porque es el índice bursátil más antiguo. Recientemente ha admitido a valores que cotizan en el Nasdaq.
NASDAQ 100: Conformado por las 100 corporaciones no financieras y con mayor valor de mercado que negocian sus acciones en el NASDAQ. La composición del índice se actualiza trimestralmente. Este índice es comúnmente utilizado como benchmark por los inversionistas posicionados fuertemente en empresas de alta tecnología. Al igual que el S&P 500, este índice responde a una fórmula de calculo en base ponderada con el valor de capitalización de las empresas que lo conforman.
Índices Composite: Los índices AMEX Composite, NYSE Composite y NASDAQ Composite, engloban la totalidad de las empresas que se negocian en sus respectivos mercados. Vienen a ser índices representativos de movimiento accionario de los tres principales mercados bursátiles. El NASDAQ Composite es el índice representativo de la evolución del Nasdaq, el mercado electrónico americano de empresas ligadas al sector tecnológico y de baja capitalización. El índice se calcula con base 100 y arranca del 5 de febrero de 1971.
Russell 1000, 2000 y 3000: el 1000 es el índice de las 1000 corporaciones más grandes de EUA; el 2000 es el índice de las siguientes 2000 más grandes; el 3000 es el índice de las siguientes 3000 más grandes.
DJ STOXX: Índice de referencia global de mercados europeos. Cuenta con 660 valores, seleccionados entre 16 países de la zona Euro, Reino Unido, Dinamarca, Suiza, Noruega, Grecia y Suecia. Se divide en 19 índices sectoriales. Pondera por capitalización y tiene base en los 1000 puntos en el 31 de diciembre de 1991. Este índice se revisa cuatro veces al año, en marzo, junio, septiembre y diciembre.
DJ Euro STOXX: Índice de referencia global en al zona Euro. Tiene 360 valores de los 11 países de la zona Euro. Pondera por capitalización y tiene base en los 1000 puntos en el 31 de diciembre de 1991. Este índice se revisa cuatro veces al año, en marzo, junio, septiembre y diciembre.
DJ STOXX 50: Índice de referencia de los "blue chips" europeos (las empresas de mayor capitalización). 50 valores de 16 países. Es más representativo que el STOXX. Pondera por capitalización y tiene base en los 1000 puntos en el 31 de diciembre de 1991. Este índice se revisa cuatro veces al año, en marzo, junio, septiembre y diciembre.
DJ Euro STOXX 50: Índice de referencia de los "blue chips" (las empresas de mayor capitalización) de la zona Euro. 50 valores de 11 países. Es más representativo que el Euro STOXX. Pondera por capitalización y tiene base en los 1000 puntos en el 31 de diciembre de 1991. Este índice se revisa cuatro veces al año, en marzo, junio, septiembre y diciembre.
FTSE 100: Conocido como el Footsie, es el índice de referencia de la bolsa de Londres. Pondera por capitalización y recoge las 100 empresas con mayor capitalización negociadas en la Bolsa de Londres. El índice se calcula con base en los 1000 puntos en el 3 de enero de 1984.
techMARK 100: El FTSE techMARK 100 recoge las 100 mayores compañías cotizadas en el techMARK, mercado de la Bolsa de Londres donde cotizan las empresas innovadoras y ligadas al sector tecnológico. Este índice pondera por capitalización. Se calcula con base en los 2000 puntos desde el 18 de octubre de 1999.
CAC 40: El CAC 40 es un índice de referencia de la bolsa de París. Recoge a las 40 empresas con mayor capitalización cotizadas en la Bolsa de París. El índice sirve de subyacente para los fututos y las opciones contratados en los respectivos mercados MATIF y MONEP, los mercados de futuros y opciones financieros de Francia. El CAC 40 se calcula con base en los 1000 puntos desde el 31 de diciembre de 1987.
DAX 30: El DAX 30, Deutschen Aktien Index, es el índice de referencia de la bolsa de Frankfurt. Selecciona a los 30 principales valores negociados en la Bolsa de Frankfurt. Pondera por capitalización. El Dax 30 tiene base en los 1000 puntos y arranca el 31 de diciembre de 1987. A partir del 18 de junio de 1999, sólo se toman para calcular el DAX aquellas empresas cotizadas en el XETRA.
NEMAX 50: El NEMAX 50 es el índice de las 50 mayores compañías cotizadas en el Neuer Markt, el mercado alemán de valores ligados al sector tecnológico. Tiene base en los 1000 puntos y arranca el 30 de diciembre de 1997. Los valores que forman parte de este índice, no pueden tener una ponderación en el mismo, superior al 10%. El NEMAX se revisa en marzo y en septiembre.
MIBTEL 30: El índice Telemático MIB recoge a las 30 mejores compañías negociadas en el sistema electrónico de la Bolsa de Milán. Pondera a los 30 valores que incluye, por capitalización. El MIB tiene base en los 10000 puntos, de 31 de diciembre de 1992.
Euro.NM All Share: El índice Euro.NM se calcula el 16 de enero de 1998 con base en los 1000 puntos el 31 de diciembre de 1997. Está compuesto por todas las empresas cotizadas en la plataforma paneuropea Euro.NM, formada por los mercados Nouveau Marché (Francia), Neuer Markt (Alemania), Euro NM Amsterdam (Holanda), Euro NM Belgium (Bélgica) y el Nuovo Mercato (Italia).
ANEXOS:
Elaboración de las tablas a través de exel:
Segundo ejemplo:
Cantidad de carne transada
Cantidad de carne transada
Cantidad de carne transada
Cantidad de carne transada
Precios de productos exportables
Precios de productos exportables
Precios de productos exportables
BIBLIOGRAFIA:
-
CORDOVA Egocheaga J, “Estadística General”, Programa avanzado de administración, Universidad San Ignacio de Loyola.
-
ESTADISTICA para administración y economía, Mc Graw - Hill
-
GUJARATI, Damodar N. (1997), “Econometría”, Tercera edición, Mc Graw - Hill, 804 pag.
-
PINDYCK & Rubinfeld. (2001), “Econometría modelos y pronósticos”, cuarta edición, Mc Graw - Hill, 639 pag.
Ver gráfica de la ecuación a través de exel y los diagramas de dispersión.
Ver forma del modelo lineal.
Esta es considerada la década perdida
Cambios estructurales son diferentes a políticas estructurales
El software asume ln como log, es por eso que en la regresion aparece log.
Sumatoria
Raíz cuadrada
Además de los índices descritos, existen muchos otros índices que representan el rendimiento de sectores determinados del mercado tales como: empresas de baja capitalización, empresas de Internet, empresas de biotecnología, etc.

X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
(f) Ninguna relación
(d) Curvilínea inversa
(c) Curvilínea directa
(b) Lineal inversa
(a) Lineal directa
![]()
![]()
(e) Lineal inversa con más dispersión

Descargar
| Enviado por: | Alfredo Zapata Rivera |
| Idioma: | castellano |
| País: | Perú |
