Diseños unifactoriales

UNIVERSIDAD DE EL SALVADOR

FACULTAD DE CIENCIAS NATURALES Y MATEMATICA

ESCUELA DE MATEMATICA

EJERCICIOS DE DISEÑOS UNIFACTORIALES PARA EL PRIMER EXÁMEN PARCIAL.

Catedrática:

Alumno:

Ciudad Universitaria, 28 de Septiembre de 2006.

Problema 4, Guía I.

Cuatro grupos de cinco vendedores de una agencia de ventas de revistas fueron sometidos a diferentes programas de entrenamiento en ventas. Debido a que no hubo deserciones durante el entrenamiento, el numeró de personas fue igual para cada grupo. Al final del programa de entrenamiento, a cada vendedor le fue asignada aleatorieamente una zona de ventas de entre un grupo de zonas que tienen aproximadamente el mismo potencial de ventas. Se desea saber si existe diferencia en los resultados promedios de los cuatro programas de entrenamiento.

• Tratamientos: Hay cuatro tratamientos que son las programas de entrenamiento. Así:

• Programa 1

• Programa 2

• Programa 3

• Programa 4.

• Factor: Tipos de entrenamiento recibidos por los vendedores.

• Niveles del factor:

• Programa 1

• Programa 2

• Programa 3

• Programa 4.

• Réplica: Es cuando se le imparte los entrenamientos a los vendedores. El número de replicaciones (replicas) es igual a cinco por tratamiento.

• Unidades experimentales: Vendedores. El número de unidades experimentales es 20.

• Variable respuesta: Resultado de los entrenamientos medido a través de las ventas realizadas por los vendedores en las zonas de ventas.

• Ejemplo 2:

Se desea saber que tipo de comerciales de televisión captan mejor la atención de los niños. Se observó la actitud de 15 niños; 5 niños fueron observados mientras veían comerciales de juguetes y juegos; 5 mientras veían comerciales sobre comida y goma de mascar y 5 mientras veían comerciales de ropa para niños. Todos los comerciales tenían 60 segundos de duración. Se miden los tiempos de atención a los comerciales.

• Tratamientos: Hay cuatro tratamientos que son los comerciales de televisión. Así:

• Comerciales de ropa para niños

• Comerciales sobre comida y goma de mascar

• Comerciales de juguetes y juegos

• Factor: son los comerciales.

• Niveles del factor:

• Comerciales de ropa para niños

• Comerciales sobre comida y goma de mascar

• Comerciales de juguetes y juegos

• Réplica: La observación repetida de la actitud de los niños hacia un tipo de comercial. El número de replicaciones (replicas) es igual a cinco por tratamiento.

• Unidades experimentales: Niños observados. El número de unidades experimentales es igual a 15.

• Variable respuesta: Atención de los niños a los comerciales.

• Ejemplo 3:

Con el propósito de comparar los precios de pan (de una determinada marca) se llevo a cabo un experimento en cuatro zonas de una ciudad. En cada una de las zonas se tomaron muestras de 8 tiendas. Se mide el precio del pan en centavos.

• Tratamientos: Hay cuatro tratamientos que son las zonas de la ciudad. Así:

• Zona 1

• Zona 2

• Zona 3

• Zona 4.

• Factor: Las diversas zonas de una ciudad.

• Niveles del factor:

• Zona 1

• Zona 2

• Zona 3

• Zona 4.

• Réplica: Es cuando se toman tiendas de una determinada zona para conocer sus precios. El número de replicaciones (replicas) es igual a ocho por tratamiento.

• Unidades experimentales: todas las tiendas muestreadas. El número de unidades experimentales es 32.

• Variable respuesta: Precio del pan en centavos.

Problema 6, Guía II.

Variable de estudio:

Contenido de carbono.







Significado verbal de las hipótesis:

Ho: No existe diferencia significativa en el contenido promedio para los tres diferentes reactores.

H1: Existe diferencia significativa en el contenido promedio para los tres diferentes reactores.

Datos:

a = 3; n = 8; N = 8.3 = 24; i = 1, 2, 3. ; j = 1,2,…, 8.

Cálculos matemáticos.





Y1. = 16,65 Y1. Barra = 2,08125

Y2. = 16,72 Y2. Barra = 2,09

Y3. = 16,31 Y3. Barra = 2,03875





Y.. = 49,68 Y.. Barra = 2,07




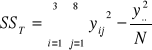
SST = 0,6856




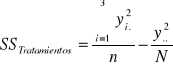
SStratamientos = 0,012025




SSE = 0,6735

La tabla ANOVA para los cálculos realizados es la siguiente:

Fuente de variación	Suma de cuadrados	g. l.	Media de cuadrados	Fo
reactores	0,012025	2	0,0060125	0,18745129
errores	0,673575	21	0,032075
total	0,6856	23

Con un alfa de 0.05 el f de tabla es F0.05, 2, 21 = 3.46

Como Fo < F0.05, 2, 21 se acepta la Ho.

Conclusión: No existe diferencia significativa en el contenido promedio para los reactores A, B y C.

Problema 21, Guía II.

a) Para este ejemplo realizamos los cálculos con el software SPSS 13.0. Las hipótesis a probar son:







Significado verbal de las hipótesis:

Ho: No existe variabilidad en el desgaste promedio para las cuatro marcas de llantas.

H1: Existe variabilidad en el desgaste promedio para las cuatro marcas de llantas.

Datos:

a = 4; n = 4; N = 4.4 = 20; i = 1, 2, 3, 4. ; j = 1,2, 3, 4.

La tabla ANOVA que nos da el SPSS se muestra a continuación.

ANOVA

desgaste

	Sum of Squares	df	Mean Square	F	P value.
Between Groups	30,688	3	10,229	2,443	,115
Within Groups	50,250	12	4,188
Total	80,938	15

Tomamos un alfa de 0.05. Ya que el P valúe es mayor que el alfa dado, se acepta Ho.

Conclusión: No existe variabilidad en el desgaste promedio para las cuatro marcas de llantas.

b) y c) Estimamos las componentes de la varianza.




= 4,188




= 1.51025




= 5.669825

d) Calculamos el intervalo de confianza con alfa igual a 0.05.




Así:

3.854<= sigma cuadrado <= 4.378

e) Calculamos un intervalo de confianza con un alfa igual a 0.1




Donde


Y


De esta manera,

0.17865 <=
<= 0.28954