Informática
Cadenas de Markov
Cadenas de Markov
Definición : Sea la secuencia x1,...,xn,...,xL; xi ![]()
X; i ![]()
{1,...,L}. Para que un proceso sea markoviano de orden n, se tiene que cumplir que:
| P{xL+1 / xL,...,x1} = P{xL+1 / xL,...,xL-n+1} |
Aunque el caso que nos ocupa es con índice "i" y variable aleatoria discretos, también hay procesos markovianos con índice y/o variable aleatoria continuos.
Definición: Un proceso markoviano de orden 1 es un proceso estocástico de orden 1 en el cual su pasado no tiene ninguna influencia en el futuro si su presente está especificado. Es decir:
Si tn-1 < tn, entonces:
P{ X(tn) ![]()
Xn/X(t) , t ![]()
tn-1 } = P{ X(tn) ![]()
Xn/X(tn-1) }
Luego, si t1 < t2 < ... < tn:
| P{ X(tn) |
En el objeto de estudio, que son las cadenas markovianas, en una cadena markoviana de primer orden se cumplirá:
| P{xL+1 / xL,...,x1} = P{xL+1 / xL} |
Definimos un estado como:
sL = {xL, xL-1, ... , xL-n+1}
Por lo tanto:
P{xL+1 / xL, xL-1, ... , xL-n+1} = P{xL+1 / sL}
De la misma manera obtenemos:
sL+1 = {xL+1, ... , xL+2-n}
P{xL+1 / xL, xL-1, ... , xL-n+1} = P{sL+1 / sL}
Por lo tanto, según se ha deducido, mediante los estados podemos pasar de una cadena de orden n a otra de orden 1, ya que hemos formado con los estados la cadena
p(s1,...,sn) = p(s1)·p(s2 / s1)·p(s3 / s2)·...·p(sn / sn-1),
que es una cadena es de orden 1.
Ejemplo: Cadena markoviana de 2º orden.
p(x1,...,xn) = p(x1,x2)·p(x3/x1,x2)·p(x4/x2,x3)·...·p(xn/xn-2,xn-1)
Si por ejemplo la secuencia es del tipo abaabbaaab..., tendremos:
p(abaabbaaab...)=p(ab)·p(a/ab)·p(a/ba)·p(b/aa)·p(b/ab)·p(a/bb)·p(a/ba)·p(a/aa)·...
Por estados:
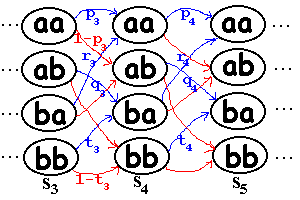
Cuando ocurre que:
| P{xL+1=j / xL=i} = P{x2=j / x1=i} |
se dice que estamos ante una cadena markoviana invariante en el tiempo u homogénea.
En el ejemplo anterior:
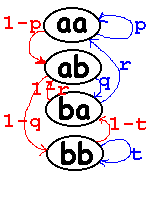
Definición: Matriz de probabilidades de transición:
P = 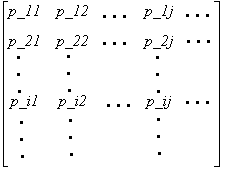
, siendo P{xn+1= j / xn= i} = pij
Propiedades de P:
Es una matriz cuadrada.
pij ![]()
0, ![]()
i,j
![]()
pij = 1
Ahora sean:
![]()
n = ( p(xn=1) , ... , p(xn=M) )![]()
n+1 = ( p(xn+1=1) , ... , p(xn+1=M) )
p(xn+1= j) = ![]()
p(xn= i, xn+1= j) = ![]()
p(xn= i)·pij
Las probabilidades de transición del estado n+1 son:
|
|
Por lo tanto, dado ![]()
1, se obtiene
![]()
n = ![]()
1·[P]n-1
Ejemplo:
Dado el diagrama de estados

una secuencia válida podría ser: abadcb...
Como cada estado depende del anterior (cadena markoviana), se observa como una característica de este ejemplo que, si el estado inicial es a, los estados a y c sólo pueden aparecer en posiciones impares de la cadena, y los estados b y d sólo en posiciones pares. Ocurriría lo mismo si el estado inicial fuera el c, y ocurriría lo contrario si el estado inicial fuera b ó d.
Periodicidad
La probabilidad de ir del estado i al estado j en n saltos se expresa como:
| Pij(n) = P{xL+n= j / xL= i} = |
La probabilidad de llegar al mismo símbolo (estado i) tras L saltos será Pii(L). Si Pii(L) ![]()
, entonces diremos que el estado i es un estado periódico de periodo d=L. Si todos los estados tienen el mismo periodo, la cadena es periódica.
Cadenas de Markov reducibles e irreducibles
Ejemplo:

Se ve claramente que Pac(n) ![]()
0, pero Pca(n) = 0, ![]()
n
Los estados conectados entre sí forman un cluster. En el dibujo hay dos, y están rodeados en rojo y azul.
Un estado es transitorio si, después de pasar por él una o varias veces, no se vuelve a pasar después por él ninguna vez más.
Si todos los estados están conectados entre sí y no son transitorios, se dice que la cadena es irreducible.
En el ejemplo anterior, hay una cadena reducible compuesta por dos cadenas irreducibles (los clusters antes mencionados). Cuando se pasa del estado b al c (transición en color verde), ya no hay manera de volver a los estados a y b. Por lo tanto, estos dos estados son transitorios en la cadena total.
Si la cadena es aperiódica, irreducible y homogénea, entonces
existe un ![]()
tal que ![]()
= ![]()
·[P]
Si en el instante n la distribución es ![]()
n = ![]()
, entonces en el instante n+1 será ![]()
n+1 = ![]()
. Por lo tanto, en una cadena de este tipo:
|
|
Una cadena de tres v.a. X, Y, Z es de Markov si cumplen:
| p(x,y,z) = p(x)·p(y/x)·p(z/y) |
Consecuencias: (para la cadena de Markov X -> Y -> Z)
-
Si Z = f(Y) => X -> Y -> Z
-
Independencia condicionada: X y Z condicionadas por Y son independientes. Entonces:
![]()
-
Simetría:

Descargar
| Enviado por: | Highlander |
| Idioma: | castellano |
| País: | México |
