Química
Química
Ejercicio 1. La fórmula de la morfina es C17H19NO3
A) ¿Cuántos átomos de oxígeno hay en un mol de morfina?. B) ¿Cuántos átomos de carbono hay en 10 mg de morfina? C) ¿Qué masa de morfina contiene 3,01 • 1023 átomos de nitrógeno? Masas atómicas: H = 1; C = 12; N = 14; O = 16.
A) Puesto que una molécula de morfina C17H19NO3 está constituida por 3 átomos de oxigeno, en 1 mol de C17H19NO3, es decir 6,02 • 1(P moléculas, habrá 3 x 6,02 • 1023 átomos de O.
B) Siendo la masa molar de C17H19NO3 igual a 285 g, igualmente, en 285 g de morfina habrá 17 x 6.02 • 1023 átomos de C.Entonces, los átomos de C que hay en 10 mg de morfina serán:
c) Del mismo modo, la masa de morfina que contiene 3,01 • 1023 átomos de N será:
Ejercicio 2. un recipiente contiene 24 cm3 de metanol. Indique:
a) Número de moléculas que contiene. b) Número de átomos de oxígeno y de carbono que contiene. c) Geometría de la molécula y tipos de enlace presentes en el metanol liquido. d) El punto de ebullición del etanol ¿será mayor o menor que el del metanol?
Razone todas las respuestas. Datos: Densidad del metanol = 0,8 g/cm3 y N = 6,023 x 1023
a) Conocida su densidad, la masa de metanol, CH3OH, de los 24 cm3 es:
m = V • d = 24 cm3 x 0,8 g/cm3 = 19,2 g, cantidad que en moles es: 19,2 g/32 g • mol-1 = 0,6 mol.
Por tanto, el número de moléculas que contiene será:
0,6 mol x 6,023 • 1023 moléc./mol = 3,614 • 1023 moléculas.
b) Como, según nos indica la fórmula, CH3OH, en cada molécula hay un átomo de C y un átomo de O, el número de átomos de estos dos elementos será también 3,614 • 1023 átomos de C y 3,614 • 1023 átomos de O. -
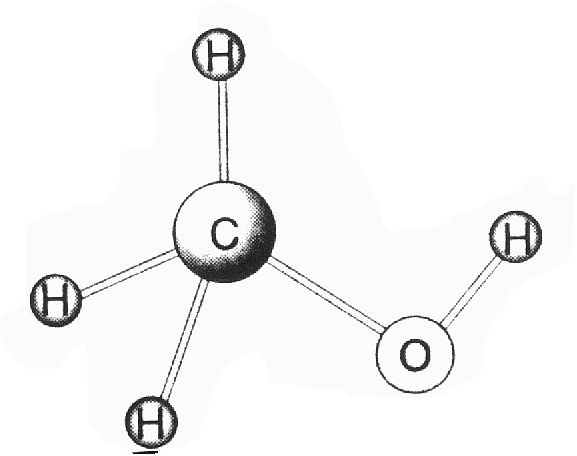
c) Ya sabemos que el C en los enlaces sencillos adopta hibridación ,s-/73, lo -que lleva consigo una distribución espacial tetraédrica de dichos enlaces (ver Castilla-La Mancha B4, pág. 77). Así pues, la geometría de la molécula de CH3 OH es básicamente tetraédrica (aunque gracias al libre giro del enÍace C-0, que repercute en la posición espacial del_ OH, puede mostrar conformaciones muy diversas).
En cuanto a los enlaces presentes en el metanol líquido, distingamos los intramoleculares de los intermoleculares. Los primeros (C-H, C-0 y 0-H) son todos covalentes, ya que se establecen entre átomos no-metálicos. Los segundos son básicamente enlaces de hidrógeno entre el O de una molécula y el H de otra molécula vecina (ver Alicante D2, pág. 13). La figura muestra estos dos aspectos:
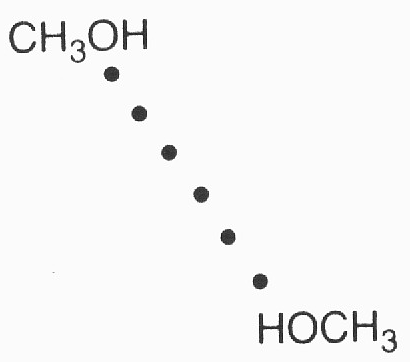
d) Los puntos de ebullición del CH3 OH y del CH3CH2OH son relativamente altos como consecuencia de los enlaces de hidrógeno existentes entre sus moléculas. No obstante, al ser las moléculas de CH3CH2OH más volumina, el CH3,CH2OH tendrá un punto de ebullición superior al CH3OH, porque las fuerzas de Van der Waals entre moléculas, aunque más pequeñas que las de enlace de hidrógeno, dependen del tamaño molecular y por ello serán más elevadas en el CH3CH2OH.
EJERCICIO 3. A) Calcular los moles de átomos de carbono, hidrógeno y oxígeno presentes en 20 g de propanona. B) ¿cuántos átomos de hidrógeno habrá en esa cantidad de acetona?
a) Los moles de propanona, CH3COCH3 o C3H6O, que son 20 g de la misma:
Como en cada mol de C3H6O hay 3 moles de C, 6 moles de H y 1 mol de O, en los 20 g habrá:
1,02 mol C 2,04 mol H 0,34 mol O
b) Teniendo en cuenta el número de Avogadro, en los 20 g de C3H6O también habrá:
2.04 mol H x 6,023 • 1023 at/mol = 1,23 • 1024 at H
Ejercicio 4. En la combustión de una muestra de 0,210 g de un hidrocarburo gaseoso, se obtienen 0,660 g de CO,. Calcule: a) 1.a fórmula empírica de este hidrocarburo. b) La fórmula molecular, si su densidad en condiciones normales es de 1'87g/L.
Datos:. R = 0,082 atm. L/ K mol Masas atómicas: H = 1; C = 12; O = 16.
La cantidad de carbono contenida en los 0,210 g de hidrocarburo será la misma que se encuentra en los 0,660 g de CO2 esto es:
Así pues. los 0,210 g de hidrocarburo están constituidos por 0.180 g de C y el resto. 0,030 g, de H.
Se halla entonces la relación en moles (o at-g)de C e H y, a continuación, se pasa a enteros dividiendo por el menor.
Como la relación en número de átomos ha de ser la misma, habrá 1 átomo de C por cada 2 átomos de H. La fórmula empírica será, pues, CH2.
b) Del dato de la densidad se deduce que 1 L de hidrocarburo gaseoso, en condiciones normales, tiene una masa de 1,87 g. Aplicando la ecuación general de los gases, pV = (m/M) KT, podemos calcular la masa molar, M, del hidrocarburo gaseoso.
de donde M = 41,9 g/mol, y el peso molecular será 41,9.
Como el «peso molecular» de la fórmula empírica. CH,, es 14, la fórmula molecular será un múltiplo (14 x 3 « 41,9) de la fórmula empírica, es decir. C3H6.
Ejercicio 5. un compuesto orgánico contiene carbono, hidrógeno y oxígeno. Al quemar completamente 5,0 g de este compuesto, se obtienen 11,9 g de dióxido de carbono y 6,1 g de agua.
a) ¿Cuál es su fórmula empírica?
b) Sabiendo que en estado de vapor 2 g de compuesto, recogidos sobre agua a 740 mm de Hg y 40 °C, ocupan un volumen de 800 mL, calcule la fórmula molecular del compuesto.
Presión de vapor del agua a 40 °C: 55 mm de Hg. Masas atómicas: carbono = 12,0; hidrógeno = 1,0; oxígeno = 16.
Al quemar un compuesto orgánico, todo su C se convierte en CO2 y todo su H, en H20. Entonces, las cantidades de C, H y O (esta última se halla por diferencia) que hay en los 5 g de compuesto son:
Y el resto será de O: 5 - (3,24 + 0,68) = 1,08 g O.
Con esta relación en gramos de C, H y O se halla la relación en -moles (o at-g) y, a continuación, se pasa a enteros dividendo por el menor:
Como la relación en número de átomos ha de ser la misma, habrá por cada átomo de 0,4 átomos de C y 10 átomos de H. La fórmula empírica será, por tanto, C4H10O.
b) Para determinar la masa molar del compuesto vamos a calcular el volumen que ocupan en condiciones normales 2 g del mismo. Como, al recogerse sobre agua, sale una mezcla de vapor de agua y vapor del compuesto, la presión de este será: 740 - 55 = 685 mm Hg.
Entonces:
Y la masa molar valdrá:
Es decir, el compuesto tiene un peso molecular de 71,2. Como el «peso molecular» de la fórmula empírica C4H10O es de 74 y aproximadamente coincide con el peso molecular calculado, la fórmula del compuesto molecular también será C4H10O
Problema 6
La densidad de un compuesto gaseoso formado por C, H y O a 250 mmHg y 300 °C es de 0,617 g/L. Al quemar 10 g de compuesto se obtienen 11,4 litros de dióxido de carbono medidos a 25 °C y 738 mmHg y 8,18 g de agua. Obtener la fórmula molecular del compuesto. Datos: R = 0,082 atm/ K. mol. Masas atómicas relativas: C = 12; O =16; H = 1.
Operando ahora de modo semejante al problema B6 de Almería, pág. 23, obtendremos que la fórmula empírica del compuesto es C2H4O.
Pasamos a continuación a calcular la masa molar del compuesto. Teniendo en cuenta que según la densidad dada. 0.617 g del mismo ocupan 1 L a 250 mmHg y 300 °C, podemos escribir:
La masa molar resulta Mm = 88,1 g/mol.
Al ser doble que la "masa molar" correspondiente a la fórmula empírica (44 g/mol), la fórmula molecular será un múltiplo de 2 de la empírica, esto es, C4H8O2
Los 11,4 L de C02 a 25 °C y 738 mm Hg ocupan en condiciones normales, según la ecuación de los gases perfectos: PV/T= PoVo/T0, V0 = 10'1 L.
Teniendo en cuenta el volumen molar y la masa molar del CO2 (44 g/mol),la masa de CO; correspondiente a los 10,1 L en c.n. es:
Podemos decir entonces que al quemar 10 g de compuesto se obtienen
19,8 g de COz y 8,18 g de HzO.
Ejercicio 7. Se ha obtenido en el laboratorio una muestra de 10,0 litros de una mezcla de H2 y CO2 a O °C y 1,7 atmósferas, determinándose que la presión parcial de CO^ era de 0,50 atmósferas. Después se eliminó el C02 y el gas restante se comprimió hasta un volumen de 1 litro a 273 °C. Determínese:
a) H número de moles de C02 en la mezcla inicial.
b) La presión final del gas hidrógeno. R = 0,082 atm • 1 • mol-1 . K-1
Como la presión total es la suma de las presiones parciales, si la presión parcial del C02 es de 0,50 atm, la del H2 será 1,20 atm (1'7 - 0'50).
Teniendo en cuenta la ley de Dalton y aplicando la ecuación de estado de los gases, averiguamos los moles de C02 y H2 que forman la mezcla.
pV = nRT
0,50 atm x 10 l =; nc = 0'023 mol CO2
1,20 atm x 10 1 = ; nH = 0'536 mol H2
b)Una vez retirado el CO2, quedan 0,536 moles de H2 ocupando 1 l a la temperatura de 273 °C. La presión del H2 en estas condiciones será:
P x 11 = 0.536 mol x 0,082 x(273 + 273) K ! P = 24,00 atm
EJERCICIO 8. Un recipiente de 20 cm3 contiene nitrógeno a 25 °C y 0,8 atmósferas. En otro recipiente de 50 cm hay helio a 25° C y 0.4 atmósferas. a) Calcule el número de moles, moléculas y átomos de cada recipiente. b) Si se unen los dos recipientes mediante un tubo capilar, ¿cuáles serán las presiones parciales de cada gas y la total del sistema? c) Calcule la concentración de cada gas en la mezcla expresándola como fracción molar y % en peso.
a) Hallamos primero los moles de N2 y He de cada recipiente aplicando la ecuación de los gases perfectos pV = nRT
De modo semejante. n(He) = 8.2 • 10-4 mol.
Para calcular el número de moléculas en los moles respectivos se ha de tener en cuenta el número de Avogadro.
6,5-10-4 mol x 6.023.1023 molec./mol = 3.9.1020 moléculas N2 y, por tanto, 2 x 3.9-1020 = 7,8-1020 átomos N
8,2.10'4 mol x 6,023-1023 molec./mol = 4,9.1020 moléculas monoatómicas He
b) Una vez mezclados los dos gases al conectar los recipientes, el volumen total será: 20 cc + 50 cc = 70 cc = 0,070 L. La presión parcial de cada componente en la mezcla es, por definición, la misma que ejercería cada uno si se estuviera solo en el recipiente.
De modo semejante, p(He) = 0,286 atm. Por tanto, la presión total: 0,227 + 0,286 =0,513 atm.
c) La concentración de cada gas en la mezcla expresada en fracción molar es:
(Obsérvese que la suma de ambos vale la unidad.)
Para hallar el porcentaje en peso calculamos los gramos de ambos gases, teniendo en cuenta la masa molar de cada uno.
N2: 6,5 •10-4 mol x 28,02 g/mol = 1.82-10-2 g N2
He: 8,2 •10-2 mol x 4.00 g/mol = 0,33 •10-2 g He
Los porcentajes en peso serán:
Ejercicio 9
Una mezcla de nitrógeno y oxígeno conteniendo un 40% en masa de nitrógeno, está a 270° C y 700 mm de presión. Calcule:
a) Presión parcial de cada gas.
b) Densidad absoluta de la mezcla a las condiciones citadas. Pesos atómicos: N = 14; 0=16.
Las presiones parciales están en función del número de moles d( cada uno y, más concretamente, de sus fracciones molares.
con lo que las presiones parciales serán:
(Compruébese que la suma de las dos fracciones molares es la unidad y que la suma de las dos presiones parciales da la presión total.)
b) La ecuación general de los gases, PV = nRT, podemos escribirla en la forma: donde n/V es el número de moles de gas por litro. Sustituyendo:
Para averiguar de esos 0,0207 moles (por litro) cuáles son de N2 y cuáles son de O2, recurrimos a las fracciones molares antes halladas.
N2 : 0,432 x 0,0207 mol = 0,0089 mol
02 : 0,568 x 0,0207 mol = 0,0118 mol
cantidades que en gramos serán:
N2: 0,0089 mol x 28 g/mol = 0.2492 g
02 : 0,0118 mol x 32 g/mol = 03776 g
Entonces, como habrá en total
0,2492 g + 0,3776 g = 0,6268 g por litro de mezcla gaseosa
La densidad de ésta será d = 0,6268 g/1.
Ejercicio 11. Un ácido clorhídrico concentrado contiene 35,2% en peso de HCI y su densidad es de 1,175 g/cm. Calcular:
a) La molaridad y la molalidad del ácido. b) El volumen de este ácido concentrado que se necesita para preparar un litro de disolución 2 molar, indicando, de forma razonada, cómo lo obtendría en el laboratorio.
Datos: Pesos atómicos: H = 1,0; O = 16,0; Cl = 35,5 g/at-g.
a) La masa de 1 litro de disolución de clorhídrico de densidad 1,175 g/cm3 es:
m = V.d = 1000 cm3 x 1,175 g/cm3 = 1.175 g.
Como la disolución es del 35,2%, las cantidades de soluto y de disolvente que componen ese litro son:
HCl y; 1175g -414g = 761g de H2O
Teniendo en cuenta las masas atómicas y moleculares, los 414 g de HCI en moles son:
HCl
Y al estar contenidos en 1 litro de disolución, la molaridad de ésta será 11.3 M.
La molalidad se calcula fácilmente recordando que por cada 761 g de H2O hay 11,3 moles de HC1:
m = 14'8
b) Un litro de disolución diluida 2M contiene 2 moles de HC1. Vamos a calcular qué volumen de disolución concentrada contiene tal cantidad de HCl:
; x = 177 cm3 disoluc. Conc.
Para preparar en el laboratorio 1 litro de disolución 2M tomaríamos 177 cm de disolución 11,3 M bien medidos mediante una probeta, lo pondríamos en un matraz aforado de 1 litro y añadiríamos agua hasta llegar a la marca del enrase, con lo que tendríamos 1 litro de disolución 2M.
Ejercicio 12.
Se dispone de una disolución acuosa de ácido nítrico del 25% en peso y densidad 1,40 g/cm3.
a) ¿Cuál es la molaridad de la disolución? •
b) ¿Qué volumen debe tomarse de esta disolución para preparar 5 litros de disolución 0,01 M?
i) Conocida su densidad, la masa de 1 L de la disolución de HNO3 del 25% es:
m = V • d == 1.000 cm3 x 1,40 g/cm3 = 1.400 g.
La cantidad de HNOg contenida en ese litro de disolución es:
1.400 x -25- = 350 g HNO3, es decir,
En consecuencia, la molaridad de la disolución será: 5,55 M.
b} Como a partir de esta disolución hay que preparar 5 L de disolución diluida 0,01 M, vamos a empezar calculando la cantidad de HNO-, que hay en estos 5 L, es decir: 5 L x 0,01 mol/L = 0,05 mol HNO-,.
El volumen de la disolución concentrada que contiene exactamente 0,05 moles de HN03 será:
A este volumen habrá que añadirle agua hasta completar los 5 L totales.
Ejercicio 13. ¿Cómo prepararía 500 mi de una disolución de ácido sulfúrico 0,4 M a partir de una disolución del mismo ácido de densidad 1.19 g/cm3, cuya riqueza es del 30%? ¿Cuál sería la fracción molar y la molalidad de la disolución concentrada = de sulfúrico? Datos: Masas atómicas: S = 32; O = 16; H = 1. -
Obtendríamos, entonces, que se necesitan 54.9 cm3 de disolución de H2S04 del 30%, y añadir agua hasta completar los 500 ml.
En cuanto a la fracción molar y molalidad de la disolución del 30%, ya que se habrá averiguado que 1 1 de ésta pesa 1.190 g. de los cuales 357 g serán de H2S04 (30%) y el resto, 833 g. de H2O. Convirtiendo estas dos cantidades en moles, tendremos que hay 3,64 moles de H2S04 por cada 46,28 moles de H2O.
Por tanto, la fracción molar (del soluto) será:
Y la molalidad : ; m = 4'37
Ejercicio 14 a) ¿Cuántos mL de una disolución de ácido clorhídrico de riqueza 40% en peso y densidad 1,2 g/mL hacen falta para preparar 0,5 litros de disolución 0,1 M de dicho ácido?
b) Describa el material de laboratorio y el procedimiento adecuado para realizar esta operación. Masas atómicas: H = 1; Cl = 35,5.
a) Vamos a calcular primero la cantidad de HC1 puro que hay en 0,5 L
de disolución 0,1 M. Como en 1 L de disolución 0.1 M hay 0.1 mol de HC1, en 0,5 L habrá la mitad de moles, esto es, 0,05 moles, que son:
0,05 mol x 36,5 g/mol = 1,82 g HC1
Los 1,82 g de HC1 necesarios para preparar la nueva disolución estarán contenidos en una cantidad de disolución del 40% de:
; x= 4'55 g x = 4,55 g disoluc. 40%
Es decir, en un volumen de:
V= m/J= 4,55 g/1,2 g-m/L = 3.8 mL disoluc. 40%
b) Así pues. tomaríamos 3,8 mL de la disolución (concentrada) del 40%. bien medidos mediante una pipeta, y los introduciríamos en un matraz aforado de 500 mL. Por último, añadiríamos agua hasta completar los 500 mL (el nivel del líquido debe llegar hasta el enrase del matraz).
Ejercicio 15. Se prepara una disolución disolviendo 180 g de hidróxido de sodio en 400 g de agua. La densidad de la disolución resultante es de 1,340 g/cm3.
a) Calcular la molaridad de la disolución.
b) Calcular los gramos de hidróxido de sodio necesarios para preparar 1 litro de disolución 0,1 M.
a) Conociendo la densidad de la disolución preparada disolviendo 180 g de NaOH en 400 g de agua, hallamos el volumen de la misma:
En este volumen de disolución hay 180 g de NaOH. es decir, 180 g/40 (g/mol) = 4,5 moles. Por tanto, la molaridad será:
b) Para preparar 1 L de disolución 0,1 M necesitaremos 0.1 mol de NaOH, esto es, 4 g.
Ejercicio 16. Se dispone en el laboratorio de una disolución de ácido clorhídrico del 32% de riqueza y densidad 1,16 g/cm3. Calcule: ==
a) La molaridad de la disolución.
b) El volumen de la disolución necesario para preparar 250 mL de disolución del 15% de riqueza y densidad 1,07 g/cm3.
a) Conocida su densidad, la masa de 1 L de la disolución de HC1 del 32% es:
m= V-d= 1.000 mLx 1,16 g/mL = 1.160g.
La cantidad de HC1 contenida en ese litro de disolución es:
En consecuencia, la molaridad de la disolución será 10,2 M.
b) Como a partir de esta disolución hay que preparar 250 mL de disolución diluida del 15% y densidad 1,07 g/mL, vamos a calcular primero la cantidad de HC1 que hay en estos 250 mL. Procediendo como antes, tenemos:
m = V • d - 250 mL x 1,07 g/mL == 267,5 g.
267,5 x 15/100=40,1 g HCL
Por último, hallamos el volumen de la disolución concentrada que contiene exactamente 40,1 g de HC1, y que será el volumen que habrá que tomar y diluir con agua hasta 250 mL para elaborar la disolución diluida.
Ejercicio 17 Se toman 100 mL de una disolución de HNO3 cuya riqueza es del 42% y su densidad 1,85 g/mL, y se diluyen hasta obtener un litro de -disolución, cuya densidad es 0,854 g/mL. Calcular: a) la fracción molar de HNO3 en la disolución resultante, b) La molalidad de la disolución resultante.
Vamos a calcular primero la cantidad de hno3 que hay en los 100 mL de disolución 42% y densidad 1,85 g/mL.
m = V • d = 100 mL x 1,85 g/mL = 185 g disolución
185 gx 42/100= 77,7 g HN03
Al diluir, esta cantidad de HNO3 se encontrará ahora en 1 L de la nueva disolución. Hallamos entonces la masa y los moles de HNO3 y H20 que componen 1 L de la nueva disolución.
m = V. d = 1 000 mL x 0,854 g/mL = 854 g disolución
compuesta por 77,7 g NHO, y por 854 - 77,7 = 776,3 g H20
o bien, y
Por tanto, la fracción molar de HNO3 será:
Y la molalidad:
NOTA: La densidad de una disolución de HNO3 >1 M no puede ser inferior a 1 g/mL. No obstante, ello no influye para nada en el desarrollo del problema.
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | España |
