Matemáticas
Matrices y determinantes
CAPÍTULO I: MATRICES
1.- DEFINICIÓN Y CLASES
-
Una matriz es un conjunto de números dispuestos en filas y columnas. Si hay m filas y n columnas, la matriz aparecerá así:
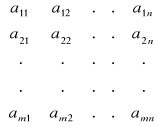
-
El elemento
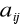
está situado en la fila i y en la columna j.
-
El número de filas y columnas

recibe el nombre de dimensión de la matriz.
-
Si m=n se dice que la matriz es cuadrada de orden n.
-
El número total de elementos de la matriz es
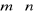
.
-
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar coinciden en su valor.
Según la forma de la matriz, esta puede ser:
-
Matriz fila: tiene una sola fila.
-
Matriz columna: tiene una sola columna.
-
Matriz cuadrada: tiene el mismo nº de filas que de columnas.
-
Matriz rectangular: no es cuadrada.
-
Matriz traspuesta: dada una matriz A, se llama traspuesta de A, y se designa por At, a la matriz que se obtiene cambiando las filas por las columnas.
-
Matriz simétrica: una matriz cuadrada es simétrica si sus elementos cumplen que
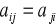
(los elementos de la diagonal principal pueden tomar cualquier valor). -
Matriz antisimétrica: se llama así a toda matriz cuadrada que cumple que
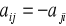
( los elementos de la diagonal principal son todos nulos).
Atendiendo a los elementos, una matriz puede ser:
-
Matriz nula: todos sus elementos son cero.
-
Matriz diagonal: es una matriz cuadrada que tiene los elementos que no pertenecen a la diagonal principal iguales a cero.
-
Matriz escalar: es una matriz diagonal en la que los elementos de la diagonal principal son iguales.
-
Matriz unidad: matriz escalar con todos los elementos de la diagonal principal iguales a uno.
-
Matriz triangular: matriz cuadrada en la que todos los elementos por encima (por debajo) de la diagonal principal son cero.
2.- OPERACIONES CON MATRICES.
2.1.- SUMA Y DIFERENCIA DE MATRICES.
-
Para sumar dos matrices, estas deben tener la misma dimensión. Cada elemento de la primera matriz se suma con su homólogo en la segunda .
-
La diferencia de matrices se defina como la suma de la primera con la opuesta de la segunda.
2.2.- PRODUCTO DE UN NÚMERO POR UNA MATRIZ.
-
Para multiplicar una matriz por un número real, se multiplica dicho número por todos y cada uno de los elementos de la matriz.
3.- PRODUCTO DE MATRICES.
3.1.- PRODUCTO DE UNA FILA POR UNA COLUMNA.
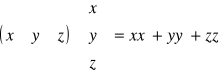
3.2.- PRODUCTO DE DOS MATRICES.
-
Dos matrices son multiplicables si el número de columnas de la primera es igual al número de filas de la segunda. La matriz producto tendrá tantas filas como la primera y tantas columnas como la segunda matriz. Se multiplicarán las filas de la primera matriz por las columnas de la segunda.
-
El producto de matrices no tiene la propiedad conmutativa.
-
Dos matrices A y B son inversas si los productos A"B y B"A son iguales a la matriz unidad.
-
Una matriz A es regular si posee matriz inversa. A la matriz inversa de A se la designa por A-1
Ejercicios:
Dadas las matrices A y B, hallar 3 A+2 B, siendo
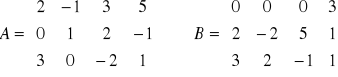
Calcular el siguiente producto de matrices:

Realizar el mismo ejercicio con las siguientes matrices:

Calcular las matrices A y B que son solución del siguiente sistema matricial:

CAPÍTULO II: DETERMINANTES
1.- DETERMINANTES DE SEGUNDO ORDEN.
Dada la matriz cuadrada de orden dos 
, se llama determinante de A al número real 
2.- DETERMINANTES DE TERCER ORDEN.
Dada una matriz cuadrada de orden tres, su determinante se calculará mediante la regla de Sarrus.

3.- PROPIEDADES DE LOS DETERMINANTES.

Si multiplicamos una fila o una columna de una matriz cuadrada por un número real, el determinante queda multiplicado por dicho número.
El determinante del producto de dos matrices es igual al producto de los determinantes.
Si permutamos dos filas (dos columnas) entre sí, el determinante cambia de signo.
Si una matriz tiene una fila (una columna) formada por ceros, su determinante es nulo.
Si una matriz tiene dos filas (dos columnas) iguales, su determinante es cero.
Si una matriz tiene dos filas (dos columnas) proporcionales, su determinante es cero.
Si una línea es combinación lineal de otras, el determinante es cero.
Si a una fila (una columna) se le suma otra fila, multiplicada por un número, el determinante no varía.
Ejercicios:
Resuelve el siguiente determinante (resta la 1ª fila a la 2ª y a la 3ª)

Haz una operación análoga para resolver el determinante siguiente:

4.- CÁLCULO DE UN DETERMINANTE POR EL ADJUNTO.
-
Dada una matriz cuadrada A, se define el adjunto del elemento aij como el determinante de la matriz resultante de eliminar la fila i y la columna j, multiplicado por (-1)i+j. Al adjunto de aij lo designaremos por Aij.
-
Si en una línea de una matriz cuadrada A sólo hay un elemento distinto de cero (aij), se verifica que

Ejercicios:
Aplica la anterior propiedad para resolver los siguientes determinantes:



5.-RANGO DE UNA MATRIZ.
-
Una línea, L, de una matriz depende linealmente de sus paralelas L1, L2, ..., Ln, si existen unos números reales a1,a2,..., an tales que verifican la igualdad:
![]()
![]()
Ejemplo: en la matriz 
la fila segunda depende linealmente de la primera, y la columna tercera depende linealmente de la primera columna y de la segunda.
-
Un conjunto de líneas paralelas de una matriz es linealmente dependiente si al menos una de ellas depende linealmente de las restantes.
-
Un conjunto de líneas paralelas de una matriz es linealmente independiente si ninguna de ellas depende linealmente de las restantes.
-
En una matriz A, el número de filas linealmente independientes es igual al número de columnas linealmente independientes. A este número se le llama rango de A.
5.1.- CÁLCULO DEL RANGO DE UNA MATRIZ.
Veamos cómo se calcula el rango de una matriz, con algunos ejemplos:
Rango de la matriz 
Rango de la matriz 
Ejercicio: demostrar que, cualesquiera que sean los números reales a, b, c, las filas F1=(0,1,c), F2=(1,a,b) y F3=(0,0,1) son linealmente independientes.
6.- MATRIZ INVERSA DE UNA MATRIZ CUADRADA.
-
La matriz inversa de una matriz cuadrada A es otra matriz A-1 tal que :
![]()
siendo I la matriz unidad.
-
Dada una matriz cuadrada A, se llama matriz adjunta de A, y se designa por adj(A), a la matriz que se obtiene al sustituir cada elemento aij por su adjunto Aij.
Ejercicio:
Calcula la matriz adjunta de la matriz 
Calcula el producto ![]()
Calcula el ![]()
Calcula el producto ![]()
¿Qué puedes deducir del resultado obtenido?
-
Si A es una matriz cuadrada regular, entonces su inversa es la matriz:

Ejemplo: vamos a calcular la inversa de la matriz 
EJERCICIOS Y PROBLEMAS
Calcular los siguientes determinantes de orden dos:

Calcular los siguientes determinantes de orden tres:

Calcular los siguientes determinantes de orden cuatro:

Calcular el rango de las matrices:

Resolver la ecuación matricial BX=C , siendo las matrices:

Si A es la matriz 
, calcular la matriz ![]()
Hallar la matriz X tal que AX=B+2C, siendo las matrices:

PROBLEMAS
Dos matrices A y B son inversas y además todos sus elementos son números enteros. ¿Cuáles son los posibles valores de det(A) y de det(B)?
En una granja se venden pollos, pavos y perdices a razón de 200, 150 y 400 ptas/kg, respectivamente. En cierta semana los ingresos totales de la granja ascendieron a 570.000 ptas. Además, se sabe que la cantidad de pollo vendida superó en 100 kg a la de pavo y que se vendió de perdiz la mitad que de pavo.
Plantea un sistema de ecuaciones para averiguar la cantidad vendida de cada uno.
Expresa matricialmente el problema.
Calcula el determinante de la matriz asociada al problema.
Resuelve el sistema mediante la matriz inversa.
EJERCICIOS DE SELECTIVIDAD
Si A y B son dos matrices cualesquiera, ¿es correcta la siguiente cadena de igualdades?
![]()
Dadas las matrices 
explica si hay alguna matriz de 2º orden X, tal que ![]()
.
Responde a las siguientes cuestiones:
Sea A una matriz de 3 filas y 4 columnas, y C una matriz de 2 filas y 3 columnas. ¿Qué dimensión tiene la matriz B sabiendo que existe el producto A"B"C?
Sea D una matriz tal que al multiplicarla por su traspuesta da una matriz de dimensión ![]()
, y el producto ![]()
es ![]()
. ¿Qué dimensión tiene D? ¿Tiene D matriz inversa?
Siendo Et=(1 2 3), calcula ![]()
Responde a las siguientes cuestiones:
Determina para qué valores de x no existe la inversa de la matriz 
Calcula A-1 para x=2.
18
1
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | España |
