Matemáticas
Matemáticas
REPERTORIO A
Hallar el valor o valores de a para los que la matriz A no tiene inversa. Hallar la inversa de A si a=2:
Hallar las dimensiones que hacen mínimo el coste de un contenedor que tiene forma de paralelepípedo rectangular sabiendo que su volumen ha de ser de 9 metros cúbicos, su altura 1 metros el coste de su construcción por metro cuadrado es de 5000 pesetas para la base, 6000 para la tapa y 4000 para cada pared lateral.
Calcular:
Una urna contiene 100 bolas numeradas así: 00, 01, 02, … , 99. Se saca una al azar. Calcular la probabilidad de que los dos números de la bola sean impares.
Un conjunto de datos bidimensionales (x,y) tiene coeficiente de correlación
r=-0,9, siendo las medias de las distribuciones marginales x=1 y=2. Se sabe que una de las cuatro ecuaciones siguientes corresponde a la recta de regresión de x sobre y:
Seleccionar razonadamente esta recta.
REPERTORIO B
Determinar los valores de m que anulan el determinante:
Dibujar la región definida por las siguientes desigualdades y determinar en ella el punto en el que la función F(x,y)=x+2y toma el valor máximo:
Representar la función:
En un proceso de fabricación el porcentaje de piezas defectuosas es del 1%. Si se fabrican 330 piezas por día, calcular la probabilidad de que el número de piezas defectuosas fabricadas en un día sea superior a 4.
Las edades en años de los asistentes a cierto curso fueron:
37, 35, 38, 36, 37, 40, 38, 25, 38
¿Cuál es la edad media de los asistentes?
La varianza del conjunto de datos anterior es 19. Las mismas personas asistirán a otro curso dentro de dos años. Obtener razonadamente la media y la varianza del nuevo conjunto de datos a partir de las correspondientes al conjunto de datos inicial.
REPERTORIO A
Dada la matriz:
calcular su inversa y comprobar el resultado.
Un supermercado quiere promocionar una marca desconocida D de aceites utilizando una marca conocida C. Para ello hace lo siguiente:
“Pague sólo a 250 pts. el litro de aceite C y a 125 el de D siempre y cuando: Compre en total 6 litros o más y la cantidad comprada de aceite C esté comprendida entre la mitad y el doble de la cantidad comprada de acite D.”
Si disponemos de 3125 pesetas, se pide:
Representar gráficamente los modos existentes de a acogerse a la oferta.
Acogiéndonos a la oferta, ¿cuál es la mínima cantidad de aceite D a la que podemos comprar? Y ¿cuál es la máxima de C?
Un objeto cae desde un avión en el instante t=0 con velocidad vertical v=10+32t metros por segundo (t=tiempo en segundos). A los 10 segundo aún no ha llegado al suelo. ¿Qué se puede afirmar sobre la altura del avión?
El volumen diario de producción en tres plantas distintas de una fábrica es de 500 unidades la primera, 1000 unidades la segunda y en la tercera 2000. Sabiendo que el porcentaje de piezas defectuosas producidas respectivamente en cada planta es del 1, 0,8 y 2 por 100. Calcular la probabilidad de que al seleccionar una unidad sea defectuosa.
Se tiene el conjunto de 26 datos:
10, 13, 4, 7, 8, 11, 10, 16, 18, 12, 3, 6, 9, 9, 4, 13, 20, 7, 5, 10, 17, 10, 16, 14, 8, 18.
Obtener su mediana y cuartiles.
REPERTORIO B
Resolver el sistema:
Dibujar la región definida por las siguientes desigualdades y determinar el punto en el que la función F(x,y)=2x+y toma el valor máximo.
Representar calculando sus máximos, mínimos y puntos de inflexión:
En una urna hay 6 bolas blancas y 3 negras, se sacan sucesivamente 3 bolas sin reemplazamiento. Calcular la probabilidad de que alguna sea negra.
En una empresa trabajan cuatro obreros. La antigüedad y el número de productos defectuosos elaborados por ellos durante el último año viene dado por:
| Antigüedad | 3 | 2 | 4 | 1 |
| Productos defectuosos | 4 | 3 | 3 | 4 |
Representar gráficamente los datos. Razonar si los datos expresan correlación positiva o negativa.
Calcular el coeficiente de correlación.
Examen de integrales (I)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
EXAMEN DE MATEMATICAS II.COU.1ªEVALUACION.
1) DADA LA SIGUIENTE FAMILIA DE SISTEMAS:
kx - 9y = k
-x + ky = 3 a)Para que valores de k no existe solucion.b)Para que valores de k el sistema es compatible determinado.Escribir la solucion.
2) DADAS LAS MATRICES:
3 1
A -2 0 1 B 0 1 C 1 2 D -9 3
1 -1 5 -1 2 3 4 -8 17
a)Resolver la ecuacion matricial AB + CX = D
b)Calcular el determinante de BA si es posible.Justificar si se puede realizar el producto.
3) DADAS LAS MATRICES QUE DEPENDEN DEL PARAMETRO K:
a)Calcular para que valores de k no hay matriz inversa.
1 0 1 b)Hallar A(elevado a -1)para k =1 si es posible.
A 1 1 -1
0 k” 0
4) LA EDAD DE UNA MADRE ES,EN LA ACTUALIDAD,EL TRIPLE QUE LA HIJA.LA SUMA DE LAS EDADES DEL PADRE,DE LA MADRE Y DE LA HIJA ES DE 80 AÑOS,Y DENTRO DE 5 AÑOS,LA SUMA DE LAS EDADES DE LA MADRE Y DE LA HIJA SERA 5 AÑOS MAS QUE LA DEL PADRE.¿CUÁNTOS AÑOS TIENEN EL PADRE,LA MADRE Y LA HIJA EN LA ACTUALIDAD?
EXAMEN DE MATEMATICAS II.COU.2ªEVALUACION.
1) UNA COMPAÑÍA PETROLIFERA REQUIERE 9tm.,12tm. y 24tm. DE PETROLEO DE CALIDAD ALTA,MEDIA Y BAJA,RESPECTIVAMENTE.LA COMPAÑÍA TIENE DOS REFINERIAS.LA REFINERIA “A” PRODUCE DIARIAMENTE 1tm,3tm y 4tm,DE CALIDADES ALTA,MEDIA Y BAJA,RESPECTIVAMENTE.LA REFINERIA “B” PRODUCE 2tm DE CADA UNA DE LAS TRES CALIDADES.EL COSTO DIARIO DE CADA UNA DE LAS REFINERIAS ES DE 2.000.000 PTS.¿CUÁNTOS DIAS DEBE TRABAJAR CADA REFINERIA PARA QUE EL COSTO SEA MINIMO?
2) UN ALMACEN DE CONFECCION DISPONE DE 70 CAMISETAS,120 CAMISAS Y 110 PANTALONES,HACE LIQUIDACION POR EXISTENCIAS.QUIERE PONERLAS A LA VENTA EN DOS TIPOS DE LOTES:EL LOTE A,FORMADO POR 2 CAMISAS,1 PANTALON Y 1 CAMISETA,SE VENDERA A 600 PESETAS CADA UNO;EL LOTE B,FORMADO POR 1 CAMISA,2 PANTALONES Y 1 CAMISETA,SE VENDERA A 700 PESETAS CADA UNO.CALCULAR CUANTOS LOTES QUE SE HAGAN DE CADA CLASE PARA OBTENER EL MAXIMO DE GANANCIAS Y CUANTO DINERO INGRESARAN POR SU VENTA.
3) EN UNA TIENDA DE MUSICA SE HA CONTADO EL NUMERO DE CANCIONES QUE TIENEN 50 DISCOS COMPACTOS SIMPLES.LOS RESULTADOS SE MUESTRAN EN LA SIGUIENTE TABLA:
NºCANCIONES:8/9/11/12/13/15/16/
CD'S:8/10/9/8/7/5/3/
A) REPRESENTA GRAFICAMENTE LOS DATOS
B) CALCULA EL NUMERO MEDIO DE CANCIONES QUE VIENE EN UN COMPACTO Y LA DESVIACION TIPICA.EXPLICAR BREVEMENTE QUE SIGNIFICA LA DESVIACION TIPICA.
C) ¿CUÁL ES EL NUMERO DE CANCIONES MINIMO DEL 30% DE LOS COMPACTOS CON MAS CANCIONES?
El profesor se cargó a toda mi clase con este examen al que dio 55' para hacerlo.
IES MEDITERRÁNEO. SALOBREÑA (GRANADA)
EXAMEN MATEMÁTICAS COU 1999-2000
PRIMER BLOQUE: FUNCIONES
1.- Dada f(x) = ax^3 + bx^2 + cx + d (NOTA= ^2= cuadrado)
Sabiendo que f ' (1) = f ' (-1) = 0 y a no es 0, determinar la función .
¿Es posible que tal función cumpla que f(0) = f(1) = 0 ?
2 puntos
nota: no te comas mucho la olla que no sale ninguna función porque siempre sale
a = 0
2.-
a) Definida f para todos los números reales como f(x) = | x+2 | | x-2 |
Hallar los puntos donde es derivable. Hallar máximos-mínimos locales.
b) Enunciar la regla de Barrow.
c) Hallar la integral definida entre 0 y 3 de 2 f(x) dx.
3 puntos
3.-
a) Enunciar la regla de L'Hopital.
b) Límites:
1
sen x
* lim ( x - 1 ) * lim ( 1 + tg x )
x -> 1 ln x sen (x-1) x -> 0 1 + sen x
2,5 puntos
4.- Siendo r > 1 y el dominio de f todos los números reales positivos y el 0
r
f (x) = x (x elevado a r)
a) Hallar la ecuación de la recta normal a la gráfica en el punto (1,1). Hacer un posible boceto.
b) Hallar el área comprendida entre la gráfica de f, su recta normal en (1,1) y el eje OX.
2,5 puntos
| EXAMEN DE MATEMATICAS DE 2º BACHILLERATO (CC.NN.) | FECHA: |
| NOMBRE: | CURSO: |
Estudia la continuidad y derivabilidad de la siguiente función:
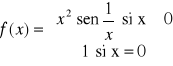
S/ Si ![]()
la función es continua y derivable por tratarse del producto de dos funciones continuas y derivables en todo su dominio. Estudiemos el caso en que x=0.
CONTINUIDAD.
f(0)=1.
![]()
por tratarse de una función que tiende a cero por otra que está acotada entre -1 y 1. El límite lateral por la derecha es exactamente igual, puesto que al aproximarnos tanto por la izquierda como por la derecha al cero lo hacemos a través de la misma rama de la función. Por tanto:
![]()
. Consecuentemente la función no es continua en x=0 (discontinua evitable) y por tanto tampoco puede ser derivable en dicho punto.
Calcula los valores de a y b para que la función siguiente sea derivable en todo R y calcula ![]()
.

S/ Estudiemos su continuidad. Si ![]()
la función es continua por tratarse de funciones polinómicas que son continuas siempre. Veamos qué pasa en x=0. f(0)=0.
![]()
![]()
Por tanto para que la función sea continua en este punto deberá ser: b=0.
Veamos ahora su derivabilidad.

Esta función es derivable en todo ![]()
por tratarse de una función polinómica y una función constante. Veamos que ocurre en x=0.
![]()
![]()
Por tanto para que la función sea continua y derivable en x=0 se tendrán que cumplir simultáneamente la ecuaciones: b=0; a=-1.Sólo en este caso la función será continua y derivable en x=0 y por tanto en todo R. En este caso:

Calcula el punto de la gráfica de la función ![]()
en que la tangente en dicho punto es paralela a la bisectriz del segundo y cuarto cuadrantes. Haz una representación gráfica y calcula dicha recta tangente.
S/ La pendiente de dicha recta tangente en el punto x (que buscamos) nos la dará: m=![]()
. Ahora bien, si es paralela a la bisectriz del segundo y cuarto cuadrante, dicha pendiente deberá ser -1, puesto que dicha bisectriz forma un ángulo de 135º con el eje de abscisas y su tangente vale -1. Por tanto ![]()
. Por último basta sustituir este valor en la función para calcular su imagen y así el punto pedido. ![]()
.
La recta tangente pedida será: ![]()
Calcula las derivadas de las siguientes funciones y simplifica si es posible:
![]()

![]()
![]()
![]()
; ![]()
![]()
![]()
Calcula el valor de los siguientes límites:



b) 

| EXAMEN DE MATEMATICAS DE 2º BACHILLERATO (CC.NN.) | FECHA: |
| NOMBRE: | CURSO: |
Estudia la continuidad y derivabilidad de la siguiente función:

Sol: Cada rama de la función es continua y derivable en donde está definida por tratarse de funciones continuas y derivables en todo su dominio (exponencial y polinómica). Donde puede existir discontinuidad es en los puntos x=0 y x=1.
Estudio de la continuidad en x=0.
![]()
![]()
![]()
. Por tanto se cumple: ![]()
y la función es continua en x=0.
Continuidad en x=1.

![]()
y la función también es continua en x=1. Consecuentemente la función es continua en todo R.
Estudio de la derivabilidad en el punto x=0.


![]()
No existe ![]()
y por tanto f(x) no es derivable en x=0.
Derivabilidad en x=1.

No existe ![]()
y por tanto f(x) no es derivable en x=1.
Consecuentemente f(x) es derivable en : ![]()
La gráfica de la función es la siguiente:
Calcula los valores de a y b para que la función siguiente sea derivable en todo R y calcula ![]()
.

Sol: Cada rama de la función es continua y derivable en sus intervalos de definición por tratarse de funciones polinómicas. Por tanto tendremos que imponer las condiciones de continuidad y derivabilidad en x=1.
Continuidad en x=1.

(I) para que f(x) sea continua en x=1. Impongamos ahora la condición de derivabilidad en dicho punto.


(II) para que f(x) sea derivable en x=1.
Resolviendo el sistema formado por las ecuaciones (I) y (II) se obtienen los valores a=1 y b=2. Entonces :

Calcula la ecuación de la recta tangente y normal a la curva de ecuación ![]()
en el punto de abscisa 1.
Sol:

Calcula las derivadas de las siguientes funciones y simplifica si es posible:
a)![]()
![]()
b) ![]()
![]()
![]()
También ![]()
Calcula el valor de los siguientes límites:
a) ![]()
b) 
Nota.- Todas las preguntas valen lo mismo.
EXAMEN PREEVALUACION. Matemáticas I. C.O.U.
Nombre:
Fecha:-
1- Sean los vectores: u (1, a, b), v, (0, a, b) y w (0, 0, 2a + b)
Halla los valores de a y b para que los tres vectores sean linealmente dependientes.
¿Podrías razonar, sin calcularlo, cual sería el rango de la matriz formada por los W -M vectores anteriores cuando a = 3 y b = 0?
2.- Aplicando las propiedades de los determinantes y sabiendo que m y n son números enteros, prueba, sin desarrollar, que el determinante siguiente es múltiplo de (m + n)2
m2 2mn n2
n2 m2 2mn
2mn n2 m2
3.- Dada la matriz:
2 0 3
A = 0 a -1
1 -1 2
a) Determina el valor de a para que exista la inversa de la matriz A.
b) Para a = 1 resuelve el sistema AX = B siendo B
1
2
-1
4.-Sea M el conjunto de todas las matrices de la forma: M x obtenidos al variar x en el conjunto de los números reales.
2x 0 0
0 1 x
0 0 1
al Prueba que al multiplicar dos matrices de M, el resultado es otra matriz del mismo conjunto M.
b] Determina, caso de existir, un valor x e IR, tal que: M(2) . M(x) =M(4)
Descargar
| Enviado por: | Stry |
| Idioma: | castellano |
| País: | España |
