Matemáticas
Matemáticas
1.- Halla la ecuación de la recta (o rectas) que pasando por el punto P (6, 2) forman un ángulo de 45º con la recta 2x - 3y = 6
2.- En el triángulo ABC siendo A (2, -3), B (-2, -2) y C (0, 3), calcula: a) La ecuación de la mediana correspondiente al vértice A; b) La ecuación de la altura correspondiente al vértice B; c) La ecuación de la mediatriz correspondiente al lado AB.
3.- Sean los puntos A (1, 3) y B (-2, -3), halla la ecuación de la recta que determinan y exprésala de todas las formas posibles, incluye la normal.
4.- Determinar las coordenadas de los vértices B y D del cuadrado que tiene por diagonal AC, donde A (1, 2) y C (9, 6). [B (7, 0) D (3, 8)]
5.- Halla las ecuaciones de las rectas que pasando por el punto A (4, 2) forman con los ejes un triángulo de área 18 u2. (2 soluciones). [x + y - 6 = 0; x + 4y - 12 = 0]
6.- Halla las ecuaciones de las rectas que pasan por el punto A (1, 1) y forman un ángulo de 45º con la recta r: 3x + 4y - 1 = 0. (Dar el resultado en forma general y canónica).
7.- Los vértices opuestos de un cuadrado se hallan en los puntos A (-2, 5) y C (2, 8). Halla la longitud y las ecuaciones de sus diagonales. [l = 5; 3x - 4y + 26 = 0; 8x + 6y - 39 = 0]
8.- Calcula el área del triángulo cuyos lados están en el eje de abscisas y en las rectas x - y = 0; 3x + 5y - 24 = 0. [S = 12 u2]
9.- Halla la ecuación de la recta que pasa por el punto de intersección de las rectas x - 2y - 4 = 0; 4x - y - 4 = 0 y forma un ángulo de 45º con la 9x - 5y - 12 = 0.
[y + 12/7 = 2/7 (x - 4/7); y + 12/7 = -7/2 (x - 4/7)]
10.- Calcula la distancia entre el origen de coordenadas y el pie de la perpendicular trazada desde el punto (2, 5) a la recta x + 2y - 1 = 0. ![]()
11.- Dado el triángulo de vértices A (0, 0), B (5, 1) y C (.3, 5), halla el circuncentro. [(24/11, 23/11)]
12.- Calcula el área del cuadrado que tienen los lados opuestos sobre las rectas 5x + 8y - 12 = 0; 10x + 16 y - 17 = 0. [S = 49/356 u2]
13.- Dada la recta 2x - 3y + 12 = 0 halla la ecuación de la mediatriz que en dicha recta interceptan los ejes de coordenadas. [3x + 2y +5 = 0]
14.- Los puntos A (1, 2), B (3, 4) y C (5, 8) son vértices de un triángulo. Halla el ortocentro. [21, -8)]
15.- Halla el área del triángulo de vértices A (-2, 1), B (5, 4) y C (2, -3). [S = 20 u2]
16.- Dada la recta de ecuación ax + by = 1, determinar a y b sabiendo que la recta dada es perpendicular a la recta de ecuación 2x + 4y = 11 y que para por el punto P (1, 3/2). [a = 4, b = -2]
17.- Los puntos A (0, 1), B (2, 3) y C (3, 9) son vértices de un triángulo. Halla el ortocentro y el área.[O (3/2, 3/2), S = 4 u2]
18.- Por el punto A (2, 6) se trazan dos rectas perpendiculares a las bisectrices del primer cuadrante y del segundo cuadrante. Halla: a) Las ecuaciones de dichas rectas; b) Las coordenadas de los vértices del triángulo formado por la recta 3x - 13y - 8 = 0 con dichas rectas. [a) x + y - 8 = 0; x - y + 4 = 0; b) P (7, 1), P' (-6, -2)]
19.- La recta y + 2 = m·(x + 3) pasa por el punto de intersección de las rectas 2x + 3y + 5 = 0; 5x - 2y - 16 = 0. Calcula m. [Punto intersec. (2, -3); m = -1/5]
20.- El punto A (2, 5) es vértice del triángulo ABC. Las ecuaciones de las rectas que contienen a las alturas hb y hc son x - 2y = 0 y 2x + 5y - 13 = 0, respectivamente. Halla la ecuación del lado a. [x - 4y = 0]
21.- Halla la ecuación de las rectas que pasando por el punto P (2, -3) forman un ángulo de 45º con la recta 3x - 4y + 7 = 0. [x + 7y + 19 = 0; 7x - y - 17 = 0]
22.- Dado el triángulo de vértices A (3, 1); B (-1, 5) y C (0, -3) halla el punto de intersección de la altura que parte de B con la mediana que parte de A.
[hB: 3x + 4y - 17 = 0; mA: y = 1; (13/3, 1)]
23.- Halla a para que la distancia del origen a la recta y = 1 + a(x - 2) sea 2. [a=-3/4]
24.- Hallar la ecuación de la recta determinada por los puntos A (-3, 0) y B (1, -5). Halla la ecuación de la paralela a AB trazada por el punto P (2, 1).
[5x + 4y + 15 = 0; 5x + 4y - 14 = 0]
25.- Calcula el valor que ha de tener m para que las rectas 2x - 3y + 5 = 0; 6x + my - 1 = 0 sean paralelas. [m = -9]
26.- ¿Están alineados los puntos (-3, 1); (0, -1/2); (4, -3)? Justificar la respuesta. [No]
27.- Halla la ecuación de la recta que pasa por el punto (2, 12) y es paralela a la bisectriz del segundo cuadrante. [y = -x + 14]
28.- Halla la ecuación de la recta que pasa por el punto (-2, 1) y tiene la dirección del vector (3, 4). [4x - 3y + 11 = 0]
29.- Halla el valor del parámetro a para que las rectas 3x - 2y =6; 3x + 4y = 0; y = ax + 1 sean concurrentes y determina el punto de intersección de las rectas. [a = -3/2; P (4/3, -1)]
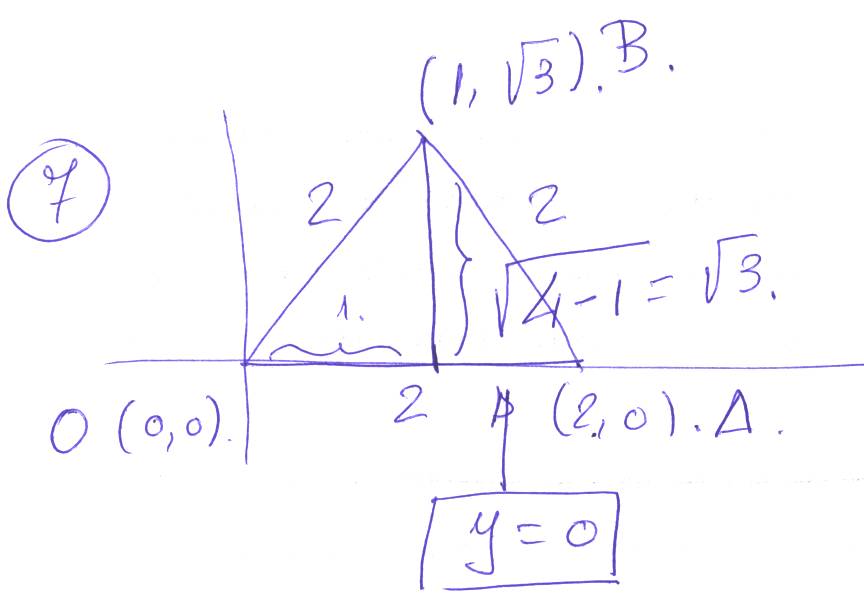
30.- Un triángulo equilátero de lado 2 tiene un vértice en el origen de coordenadas y otro en el semieje positivo. Halla las ecuaciones de sus lados. ![]()
31.- Los puntos P (-1, 2); Q (4, 0); R (2, -3) son tres vértices consecutivos de un paralelogramo PQRS. Se pide hallar las coordenadas del vértice S y las ecuaciones de las diagonales. [S (-3, -1); PR: 5x + 3y - 1 = 0; SQ: x - 7y - 4 = 0]
32.- Dados los puntos A (2, 3); B (-1/3, 4) y C (-4, 0) calcula: a) La ecuación de la recta determinada por A y B; b) Ecuación de la recta que pasa por C y es paralela a la anterior. [a) 3x + 7y - 27 = 0; b) 3x + 7y + 12 = 0]
33.- Dadas las rectas r: 2x + y + 5 = 0 y r': 2x - 3y - 8 = 0, halla la ecuación de la recta paralela a r que pasa por el punto en que r' corta al eje OX. [y = -2x + 8]
34.- Dadas las rectas 3x - y + 1 = 0; 2x + y - 3 = 0 determina a para que la recta de ecuación ax - 3y + 5 = 0 pase por el punto de intersección de las otras dos. [a = 4]
35.- Calcula el valor de a para que las rectas 3x - y + 9 = 0; ax + 2y - 1 = 0 sean paralelas. [a = -6]
36.- Determinar a y b sabiendo que las rectas ax + y - 1 = 0; 3x + by - 5 = 0 son paralelas y que la primera pasa por el punto (1, -5). [a = 6, b = ½]
37.- Dados los puntos A (1, -3) y B (-2, 3) halla a para que la recta ax + y + 5 = 0 sea paralela a la recta AB. [a = 2]
38.- Dada la recta r de ecuación 3x - y + 1 = 0, calcula b sabiendo que el punto (2, b) está en la recta que pasa por el punto (0, -4) y es paralela a r. [b = 2]
39.- Halla las ecuaciones de los lados del triángulo de vértices A (1, 4/3), B (-4, 4/3) C (-4, 4). [AB: 3y - 4 = 0; AC: 8x + 15y - 28 = 0; BC: x + 4 = 0]
40.- Calcula el valor de a para que los puntos A (-7, 2), B (3, 7/2) y C (a, 7) estén alineados. [a = 79/3]
41.- Hallar el coeficiente m para que las rectas ![]()
sean concurrentes. ¿Cuál es el punto común? [m = ½; P (4, 3)]
42.- Dados los puntos A (-1, 0), B (2, 1) y C ½, 3), se pide: a) Determinar las coordenadas del punto D sabiendo que ABCD son vértices consecutivos de un paralelogramo; b) Halla el punto de intersección de las diagonales. [a) D (-5/2, 2) b) (-1/4, 3/2)]
43.- El eje OX y las tres rectas y = 1, x + 2y - 2 = 0; x + 2y - 6 = 0, limitan un cuadrilátero. Halla las ecuaciones de sus diagonales y las coordenadas de su punto de intersección. [x - 2y - 2 = 0; x + 6y - 6 = 0 Punto corte (3, ½)]
24.- Hallar la ecuación de la recta determinada por los puntos A (-3, 0) y B (1, -5). Halla la ecuación de la paralela a AB trazada por el punto P (2, 1).
[5x + 4y + 15 = 0; 5x + 4y - 14 = 0]
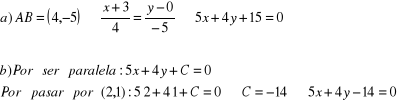
25.- Calcula el valor que ha de tener m para que las rectas 2x - 3y + 5 = 0; 6x + my - 1 = 0 sean paralelas. [m = -9]
![]()
26.- ¿Están alineados los puntos (-3, 1); (0, -1/2); (4, -3)? Justificar la respuesta. [No]
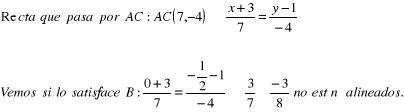
27.- Halla la ecuación de la recta que pasa por el punto (2, 12) y es paralela a la bisectriz del segundo cuadrante. [y = -x + 14]
Bisectriz del 2º cuadrante: y = -x x + y = 0.
La recta es: x + y + C = 0. Por pasar por (2, 12) 2 + 12 + C = 0 C = -14
x + y - 14 = 0
28.- Halla la ecuación de la recta que pasa por el punto (-2, 1) y tiene la dirección del vector (3, 4). [4x - 3y + 11 = 0]
![]()
29.- Halla el valor del parámetro a para que las rectas 3x - 2y =6; 3x + 4y = 0; y = ax + 1 sean concurrentes y determina el punto de intersección de las rectas. [a = -3/2; P (4/3, -1)]
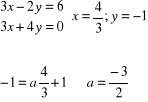
30.- Un triángulo equilátero de lado 2 tiene un vértice en el origen de coordenadas y otro en el semieje positivo. Halla las ecuaciones de sus lados. ![]()

31.- Los puntos P (-1, 2); Q (4, 0); R (2, -3) son tres vértices consecutivos de un paralelogramo PQRS. Se pide hallar las coordenadas del vértice S y las ecuaciones de las diagonales. [S (-3, -1); PR: 5x + 3y - 1 = 0; SQ: x - 7y - 4 = 0]

Si es un paralelogramo: ![]()

![]()
![]()
32.- Dados los puntos A (2, 3); B (-1/3, 4) y C (-4, 0) calcula: a) La ecuación de la recta determinada por A y B; b) Ecuación de la recta que pasa por C y es paralela a la anterior. [a) 3x + 7y - 27 = 0; b) 3x + 7y + 12 = 0]

![]()
33.- Dadas las rectas r: 2x + y + 5 = 0 y r': 2x - 3y - 8 = 0, halla la ecuación de la recta paralela a r que pasa por el punto en que r' corta al eje OX. [y = -2x + 8]
Paralela a r: 2x + y + d = 0
Punto de corte de r' con OX y = 0 2x - 8 = 0; x = 4; (4, 0)
Por pasar por (4, 0) 8 + d = 0 d = -8
2x + y - 8 = 0
34.- Dadas las rectas 3x - y + 1 = 0; 2x + y - 3 = 0 determina a para que la recta de ecuación ax - 3y + 5 = 0 pase por el punto de intersección de las otras dos. [a = 4]
Punto de intersección: ![]()
![]()
![]()
4x-3y+5 = 0
35.- Calcula el valor de a para que las rectas 3x - y + 9 = 0; ax + 2y - 1 = 0 sean paralelas. [a = -6]
![]()
36.- Determinar a y b sabiendo que las rectas ax + y - 1 = 0; 3x + by - 5 = 0 son paralelas y que la primera pasa por el punto (1, -5). [a = 6, b = ½]
ax + y - 1 = 0 (1, -5) a = 6
3x + by - 5 = 0 ![]()
37.- Dados los puntos A (1, -3) y B (-2, 3) halla a para que la recta ax + y + 5 = 0 sea paralela a la recta AB. [a = 2]
A (1, -3)
B (-2, 3)
![]()
ax + y + 5 = 0
![]()
38.- Dada la recta r de ecuación 3x - y + 1 = 0, calcula b sabiendo que el punto (2, b) está en la recta que pasa por el punto (0, -4) y es paralela a r. [b = 2]
r: 3x - y + 1 = 0
3x - y + d = 0 d = -4
3x - y + 1 = 0; 3·2 - b - 4 = 0 b = 2
39.- Halla las ecuaciones de los lados del triángulo de vértices A (1, 4/3), B (-4, 4/3) C (-4, 4). [AB: 3y - 4 = 0; AC: 8x + 15y - 28 = 0; BC: x + 4 = 0]



40.- Calcula el valor de a para que los puntos A (-7, 2), B (3, 7/2) y C (a, 7) estén alineados. [a = 79/3]

41.- Hallar el coeficiente m para que las rectas ![]()
sean concurrentes. ¿Cuál es el punto común? [m = ½; P (4, 3)]

42.- Dados los puntos A (-1, 0), B (2, 1) y C (½, 3), se pide: a) Determinar las coordenadas del punto D sabiendo que ABCD son vértices consecutivos de un paralelogramo; b) Halla el punto de intersección de las diagonales. [a) D (-5/2, 2) b) (-1/4, 3/2)]



43.- El eje OX y las tres rectas y = 1, x + 2y - 2 = 0; x + 2y - 6 = 0, limitan un cuadrilátero. Halla las ecuaciones de sus diagonales y las coordenadas de su punto de intersección. [x - 2y - 2 = 0; x + 6y - 6 = 0 Punto corte (3, ½)]

|
|
|
|
|
|

2
10
Descargar
| Enviado por: | Joselu |
| Idioma: | castellano |
| País: | España |




