Física
Lentes y formación de imágenes
LENTES, IMÁGENES E INSTRUMENTOS ÓPTICOS.
OBJETIVO GENERAL.
Aplicar el enfoque de la óptica geométrica a la descripción de las imágenes formadas por lentes y sistemas ópticos.
OBJETIVOS ESPECÍFICOS.
• Observar las imágenes formadas en varios arreglos de lentes
• Calcular la distancia focal y el aumento lateral de los arreglos en condiciones especificas.
Analizar el comportamiento de la luz en estos sistemas y la utilidad del enfoque geométrico en la óptica.
INTRODUCCIÓN TEÓRICA.
Sin duda el sistema óptico más usado es la lente y eso pese al hecho de que vemos el mundo a través de un par de ellas.
Los lentes toma una gran variedad de formas, por ejemplo, hay lentes acústicas y de microondas; algunas de las últimas se hacen de vidrio o cer en formas fácilmente reconocibles mientras que en otras son bastante más sutiles en apariencia. En el sentido tradicional, una lente es un sistema óptico formado por dos o más interfases refractoras donde al menos una de estás está curvada.
Cuando una lente está formada por un elemento, es decir, cunado tiene sólo dos superficies refractoras, es una lente simple. La presencia de más elementos la hace una lente compuesta. Una lente se puede clasificar también en delgada o gruesa, bien sea que su grueso efectivo sea despreciable o no.
La lentes que se conocen como convexas, convergentes o positivas, son más gruesas en el centro y así tienden a disminuir el radio de curvatura de los frentes de onda, es decir, la onda se hace más convergente conforme atraviesa la lente. Esto es, por supuesto, suponiendo que el índice de la lente es mayor que el del medio en que está sumergida.
Por otro lado, las lentes cóncavas, divergentes o negativa!, son más delgadas en el centro y tienden a avanzar esa porción del frente de onda haciéndola más divergente de lo que era al entrar
La siguiente figura muestra secciones transversales de varias lentes simples esféricas centradas:
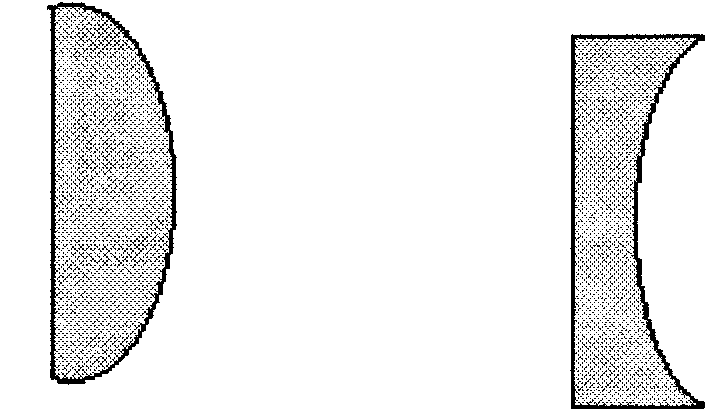
Biconvexo Plano convexo Plano cóncavo
Para conocer la distancia focal de una lente convergente se utiliza el método de Planos conjugados que conlleva la siguiente fórmula:
F= d2 - (X2 - X,) 2
4d
El doblete de contacto se utiliza para conocer distancias focales de lentes negativas:
f = fs fp
fp-fs
SISTEMAS OPTICOS.
OCULAR.
Es un instrumento óptico visual, fundamentalmente es una lupa y su función no es ver un objeto físico real, si no la imagen intermedia de ese objeto. El aumento lineal del ocular está dado por:
m = - ¡/o
MICROSCOPIO COMPUESTO.
Es el siguiente paso de la lupa simple y da mayor aumento angular de objetos cercanos. El sistema de lentes que está cerca del objeto, que aquí es una lente simple, recibe el nombre de objetivo. Forma una imagen real del objeto, invertida y generalmente aumentada. El ocular aumenta esta imagen intermedia aún más. Entonces el poder de aumento del sistema M es el producto de la amplificación lineal m del objetivo y la amplificación angular m, del ocular, o sea:
M = m m. = (-s/fob)(25cm/foc)
TELESCOPIO.
Es un sistema para ver a distancia (que es el significado de la palabra teleskopos en griego). El telescopio construido por Galileo consta de una lente negativa como ocular y una positiva como objetivo y formaba una imagen erecta. En la práctica, la posición intermedia está fija y solamente se mueve el ocular para enfocar el instrumento. La imagen final está invertida. El aumento angular es:
M= -fob/foc.
MATERIAL Y EQUIPO
Juego de lentes
Lámpara con fuente
Regla o flexómetro
DESARROLLO EXPERIMENTAL
EXPERIMENTO 1
a) Sobre el riel óptico montar un dispositivo como se muestra en la figura. d
b) Colocar una lente biconvexa de distancia focal conocida y un
objeto(diafragma con ranura de forma de flecha). La pantalla debe tener
de preferencia una cuadricula con línea tenue para medir el tamaño de la
imagen.
c) Seleccione una distancia objeto arbitraria.
d) Mueva la pantalla hasta lograr una imagen bien definida. Mida la distancia imagen y el tamaño de la misma.
e) Realice lo anterior para 5 distancias objeto.
RESULTADOS.
Los resultados de esta experiencia fueron los siguientes:
Tamaño original del objeto: 0.5cm
| DISTANCIA OBJETO | DISTANCIA IMAGEN | TAMAÑO IMAGEN |
| 2 cm | 2.1 cm | 1 cm |
| 3 cm | 3.2 cm | 1 cm |
| 4 cm | 4 cm | 0.7cm |
| 5 cm | 5 cm | 2.5cm |
| 6 cm | 6.5 cm | 2cm |
| 7 cm | 7.8 cm | 1.7cm |
| 8 cm | 8.9 cm | 1.5 cm |
| 9 cm | 10.2 cm | 1.2 cm |
| 10 cm | 10.9 cm | 1cm |
| 11 cm | 12.5 cm | 0.2 cm |
| 12 cm | 13.8 cm | 0.8 cm |
| 13 cm | 15.1 cm | 0.5 cm |
| 14 cm | 16 cm | 0.2 cm |
| 15 cm | 17.70 cm | 0.1 cm |
ANALISIS DE RESULTADOS.
a) Determine la localización de la imagen para cada uno
De la introducción teórica se extrae la fórmula:
1 + 1 = 1
o i f
y como se utilizó una lente de distancia focal conocida, esta distancia es f = 100 cm de la fórmula se despeja i (distancia de la imagen):
1 = 1 - 1
i f o
Los cálculos se muestran en la tabla siguiente:
| Distancia del objeto (o) | 1 = 1 - 1 i f o |
| 2 cm | 2.04 cm |
| 3 cm | 3.09 cm |
| 4 cm | 4.16 cm |
| 5 cm | 5.26 cm |
| 6 cm | 6.38 cm |
| 7 cm | 7.52 cm |
| 8 cm | 8.69 cm |
| 9 cm | 9.89 cm |
| 10 cm | 11.11 cm |
| 11 cm | 12.35 cm |
| 12 cm | 13.62 cm |
| 13 cm | 14.94 cm |
| 14 cm | 16.27 cm |
| 15 cm | 17,64 cm |
Haciendo una comparación con los observado experimentalmente y obteniendo el error porcentual entre ellos, tenemos que:
| Distancia imagen obs. (Ve) | Distancia imagen calculada (Vt) | E%= Vt - Ve Vt |
| 2.1 cm | 2.04 cm | 2.94% |
| 3.2 cm | 3.09 cm | 3.55% |
| 4.0 cm | 4.16 cm | 3.8% |
| 5.0 cm | 5.26 cm | 4.9% |
| 6.5 cm | 6.38 cm | 1.8% |
| 7.8 cm | 7.52 cm | 3.72% |
| 8.9 cm | 8.69 cm | 2.41% |
| 10.2 cm | 9.89 cm | 3.13% |
| 10.9 cm | 11.11 cm | 1.89% |
| 12.5 cm | 12.35 cm | 1.21% |
| 13.8 cm | 13.62 cm | 1.32% |
| 15.1 cm | 14.94 cm | 1.07% |
| 16.0 cm | 16.27 cm | 1.65% |
| 17.7 cm | 17.64 cm | 0.34% |
Si se hace un promedio de los E%, se encuentra que el error porcentual es de 2.04%, lo cual no significa una gran diferencia y nos da a entender que hay un equilibrio, entre lo que se observó y lo que se calculó.
a) Con los datos anteriores encuentre para cada medida el aumento de la lente, haciendo un promedio.
El aumento m de la lente se da por:
m = - i / o
La siguiente tabla muestra el cálculo y los resultados:
| Distancia objeto (o) | Distancia imagen (i) | m = -¡/o |
| 2 | 2.04 | m=-(2.0.4)(2)=1.02 |
| 3 | 3.09 | m=-(3.09)(3)=1.03 |
| 4 | 4.16 | m=-(4.16)(4)=1.04 |
| 5 | 5.26 | m=-(5.26)(5)=1.05 |
| 6 | 6.38 | m=-(6.38)(6)=1.06 |
| 7 | 7.52 | m=-(7.52)(7)=1.07 |
| 8 | 8.69 | m=-(8.69)(8)=1.08 |
| 9 | 9.89 | m=-(9.89)(9)=1.09 |
| 10 | 11.11 | m=-(11.11)(10)=1,11 |
| 11 | 12.35 | m=-(12.35)(11)=1.12 |
| 12 | 13.62 | m=~(13.62)(12)=1.13 |
| 13 | 14.94 | m=-(14.94)(13)=1.14 |
| 14 | 16.27 | m=-(16.27)(14)=1.16 |
| 15 | 17.64 | m=-(17.64)(15)=1.17 |
Sacando el promedio encontramos que el aumento de la lente es: m = 1.09
EXPERIMENTO II
Medición de distancias focal por el método de los planos conjugados
a) Con el mismo montaje anterior fije una distancia d entre el objeto y la pantalla
b) Desplace la lente desde muy cerca del objeto hasta que se forme una imagen nítida en la pantalla, en caso de que no se forme imagen aumente la distancia d. c) Una vez que se haya formado la imagen, continúe desplazando la lente hasta formar nuevamente una imagen sobre la pantalla, mida estas dos distancias.
RESULTADOS.
La siguiente tabla muestra la distancia entre el objeto y la pantalla, así como las distancias donde se forma una imagen nítida, una cercana al objeto (X1) y otra cercana a la pantalla (X2):
| Distancia obj. - pantalla | xi | X2 |
| 20 cm | 7.7 cm | 13.5 cm |
| 25 cm | 6.7 cm | 18.8 cm |
| 30 cm | 6.2 cm | 24.2 cm |
| 35 cm | 6.0 cm | 30.3 cm |
ANALISIS DE RESULTADOS.
Calcular la distancia focal para la lente convergente (lente biconvexa). Para esto se necesita de la fórmula de planos conjugados que es:
F= d2 + (X2 - X,) 2
4d
Para cada distancia:
d = 20 cm
f = (20) 2+ (13.5 - 7.7) 2
4(20) = 4.6 cm
d= 25 cm
f = (25) 2+ (18.8 - 6.7) 2
4(25) = 4.8 cm
d=30cm
f = (30) 2+ (24.2 - 6.2) 2
4(30) = 4.8 cm
d = 35 cm
f = (35) 2+ (30.3 - 6.0) 2
4(35) = 4.5 cm
Haciendo un promedio vemos que la distancia focal es de:
f = 4.68 cm
¿Es necesario considerar las dimensiones del objeto y la imagen? ¿Por qué?
En este caso no por que se está trabajando con una fórmula que sólo implica a distancias en las que se forma una imagen nítida sin tomar en cuenta el tamaño de ésta.
EXPERIMENTO III
Medición de distancia focal de una lente delgada bicóncava (negativa) por el método del doblete en contacto.
Utilice el mismo montaje anterior.
Coloque una lente delgada positiva de distancia focal conocida en contacto con una lente negativa cuya distancia focal se desea determinar.
Determine por el método de los planos conjugados la distancia focal de la combinación
RESULTADOS.
Al aplicar la lente negativa al sistema se obtuvieron los siguientes datos de d, X1 y X2. A continuación se presentan los datos organizados en una tabla:
Distancia focal X1 X2
| 30 cm | 9 cm | 23.5 cm |
| 35 cm | 8.7 cm | 29 cm |
| 40 cm | 13.4 cm | 34.4 cm |
| 45 cm | 8.3 cm | 39.4 cm |
ANALISIS DE RESULTADOS.
a) Calcular la distancia focal f mediante el método de doblete de contacto. La fórmula de este método es:
fn = (fs fp) / (fP - f5)
donde f,, es la f de la lente negativa, f. la f de la lente positiva y fr, de el sistema.
Con los datos que se obtuvieron se calcula la fs:
fs = d2 - (X2 - X,) 2
4d
f s = (30) 2 - (23.5 - 9) 2
4(30) = 7.37 cm
f s = (35) 2 - (29 - 8.7) 2
4(35) = 8.60 cm
f s = (40) 2 - (34.4 - 13.4) 2
4(40) = 7.24 cm
f s = (45) 2 - (39.4 - 8.3) 2
4(45) = 5.87 cm
Y el promedio es = 7.27 cm
Como se conoce la f de la lente positiva:
fn = fs fp = (7.27) (4.68) = -13 14 cm.
fp - fs (4.68) - (7.27)
el signo negativo indicará que la imagen es invertida.
b) ¿Cuáles deben ser las condiciones para poder medir la distancia focal de la lente bicóncava con ayuda de la lente biconvexa?
- Que la lente positiva debe ser de una distancia focal mayor que la lente negativa, para que se tome una lente positiva.
- Que la lente negativa este entre los rayos luminosos y la lente positiva, para que así se concentre en esta última los rayos y se formen las imágenes.
EXPERIMENTO IV
MICROSCOPIO
Para el arreglo para microscopio colocar en el banco óptico, sin lámpara, una lente convergente de distancia focal pequeña (entre 8 y 12 Cm.) que servirá como ocular. Sobre la pantalla, en el otro extremo colocar un objeto pequeño. Montar otra lente en medio, también de distancia focal conocida pequeña, pero más cerca del objeto que del ocular, esta lente se llamará objetivo.
Mover el ocular y/o el objetivo hasta lograr la mayor amplificación con la mejor nitidez. El objetivo debe colocarse a una distancia del objeto un poco mayor que el foco de la misma y la longitud total del instrumento debe ser la suma de las distancias focales. Medir las distancias entre cada uno de los elementos del sistema y observar las imágenes.
Tome como objeto ahora una ranura circular de diámetro conocido, coloque una regla a la distancia de visión nítida (aprox. 25 cm.) y determine el diámetro de la imagen.
Invertir la posición de las lentes, observar las imágenes obtenidas.
RESULTADOS.
El sistema que se monto utilizo dos lentes positivas una de f = 300 y otra de f =100, a continuación se muestra el resultado:
ANALISIS DE RESULTADOS.
A) Calcular el arreglo lateral total para el microscopio.
Está dado por:
Atot = MaMt
donde:
Ma = aumento angular del ocular = 3/f = 25 cm/300 = 0.833cm
Mt = aumento lineal del objetivo = L/f = 1/100 = 0.01cm
donde L = longitud del tubo (distancia del 2o foco del objetivo a el 1er ocular).
Atot = MaMt = (0.833 cm)( 0.01 cm )= 8 .33 x 10-3
TELESCOPIO
-
Use como objetivo una lente positiva de distancia focal grande y como ocular una distancia focal corta, siendo la longitud del instrumento la suma de las distancias focales.
Observe objetos alejados.
Use ahora una lente positiva de distancia focal corta(lente erectora), colóquela en la posición del ocular y separe este hasta una distancia de 4 veces la distancia focal de la lente erectora. La modificación hecha al telescopio anterior lo transforma en un catalejo.
Cambiar el ocular por una lente divergente manteniendo la lente objetivo convergente de distancia focal mayor. Enfocar algún objeto lejano y una vez determinada la posición de las lentes medir la distancia entre ellas registrando también las características de las imágenes. (Telescopio e Galileo).
RESULTADOS.
Se ocuparon dos lentes: una +300 y otra -100, el sistema quedó de la siguiente manera:
ANALISIS DE RESULTADOS.
A) Calcular el aumento angular total.
Sabiendo que el aumento total angular del telescopio está dado por:
Mo = f objetivo = -300/100 = -3 cm
f ocular
El signo negativo indica que al imagen está invertida.
b) Hacer un análisis comparativo para explicar lo observado en los sistemas ópticos.
Microscopio Telescopio ------
*2 lentes positivas *una positiva y otra negativa
*corta distancia entre lentes *gran distancia entre lentes
Como sabemos en el telescopio lo que se requiere no es aumentar de tamaño un objeto sino "acercarlo", por lo cual requiere de la lente negativa y en el microscopio el objetivo es aumentar por lo cual la distancia entre lentes es corta y Las lentes son positivas.
CUESTIONARIO.
- POR QUE NO PUEDE UTILIZAR SE EL METODO DE LOS PLANOS CONJUGADOS PARA DETERMINAR DISTANCIA FOCAL DE UNA LENTE NEGATIVA DIRECTAMENTE?.
Por que en los lentes planos la imagen de cualquier figura es siempre virtual y derecha conservando siempre sus dimensiones..
- CUAL ES LA DIFERENCIA ENTRE UN MICROSCOPIO COMPUESTO Y UNO SIMPLE?
Que el microscopio compuesto es mas elaborado, se compone de dos lentes de distancia focal pequeña, llamadas objetivo y ocular; y el microscopio simple es el que solo tiene una convergente comúnmente conocida como lupa.
- CUALES SON LAS FUNCIONES DEL OBJETIVO Y EL OCULAR?
El objetivo es el sistema de lentes que esta cerca del objeto. Forma una imagen real del objeto, invertida y generalmente aumentada. Y el ocular aumenta la imagen intermedia aun mas.
- INVESTIGUE: CUAL ES EL SISTEMA OPTICO UTILIZADO EN LOS PRISMATICOS? REALICE UN DIAGRAMA DE LOS MISMOS.
Es un sistema similar al telescopio de Galileo. Este consta de una lente divergente como ocular y una lente convergente. La ventaja de este sistema es que la imagen virtual amplificada no esta invertida si no correcta.
Pupila de salida
![]()
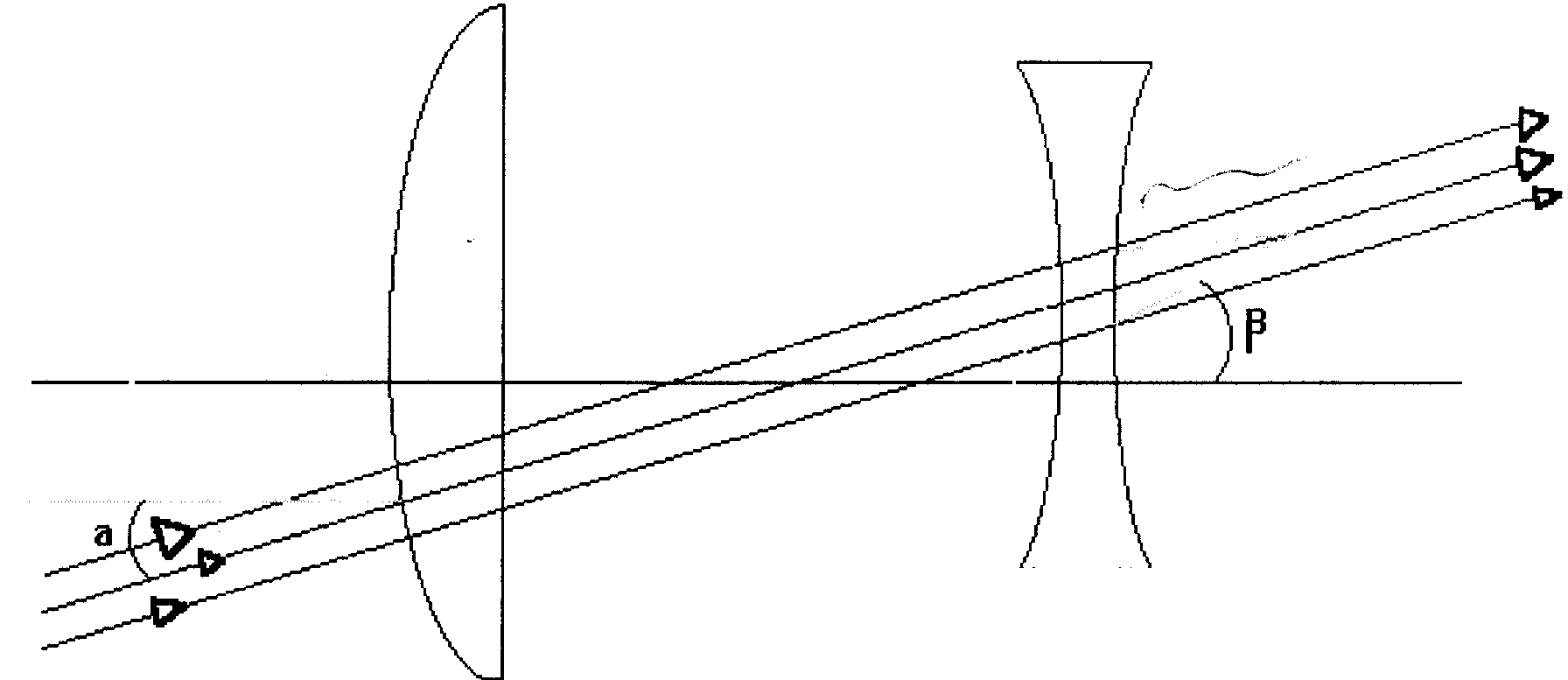
OCULAR
- EXPLIQUE EL FUNCIONAMIENTO OPTICO DEL OJO HUMANO.
El ojo es le instrumento óptico mas básico. Los rayos paralelos que penetran en un ojo relajado que mira al infinito, producen una imagen real e invertida sobre la retina. En estas condiciones el ojo actúa como una lente convergente. La mayor parte de la relación se produce en la superficie externa del ojo, llamada cornea.
-QUE SE HACE PARA CORREGIR LA MIOPIA Y LA HIPERMETROPIA?
Para corregir la miopía colocamos una lente adicional en frente del ojo tal que la combinación anteojo-sistema de lente del ojo tenga un segundo punto focal en la retina. Ya que el ojo miope puede ver claramente los objetos mas cercanos que el punto lejano, la lente del anteojo debe formar imágenes relativamente cercanas de los objetos distantes. Por consiguiente introducimos una lente negativa que diverja los rayos un poco.
Para corregir la hipermetropía se debe colocar una lente positiva enfrente del ojo.
CONCLUSIONES
Durante el desarrollo de la presente práctica se pudo conocer el funcionamiento de los diferentes tipos de lentes, así como las imágenes que forman.
Los diferentes tipos de arreglos de lentes también fueron estudiados en esta experiencia, de ellos se pudo conocer las imágenes que forman, los tipos de lentes que usan y su aplicación en la vida diaria. Por ejemplo se estudio el funcionamiento del ojo humano que es el sistema más importante para nosotros, ya que a través de él vemos el mundo que nos rodea.
Por otro lado se pudo calcular la distancia focal y el aumento lateral de dichos arreglos aplicando las fórmulas que se investigaron para completar la introducción teórica. Estos resultados fueron satisfactorios ya que los errores encontrados no fueron grandes en comparación con lo experimentado.
Finalmente se puede decir que los objetivos de ésta práctica se cumplieron de un modo aprobatorio.
BIBLIOGRAFIA.
- Hecht, Zajac, Qpfic Addison - Wesley Iberoamericana, EE.UU.AA., 1986,
pp. 107 - 165.
- Resnik, Halliday, Física Vol. II Compañía Editorial Continental, México, 1994, pp. 360 - 386.
Descargar
| Enviado por: | Jimini |
| Idioma: | castellano |
| País: | México |
