Matemáticas
Estadística
Experimentos
Existen dos tipos de experimentos:
-
Experimentos Deterministas: Son aquellos cuyos resultados se pueden predecir de antemano.
-
Experimentos Aleatorios: Son aquellos cuyos resultados son impredecibles.
Llamaremos Prueba, al proceso mediante el cual se obtiene un resultado.
Se llama Espacio Muestral de un experimento aleatorio, al conjunto de todos los resultados posibles del experimento. Lo representaremos por la letra E.
Sucesos Aleatorios
Llamamos Suceso de un experimento aleatorio (o simplemente Suceso Aleatorio) a cada uno de los subconjuntos del Espacio Muestral E. El Conjunto de todos los sucesos de un experimento aleatorio se denomina Espacio de Sucesos y se representa por la letra S.
Ejemplo:
Determinar el espacio muestral y el espacio de sucesos del experimento aleatorio que consiste en lanzar una moneda y anotar el resultado de la cara superior.
Solución:
El Espacio Muestral será el conjunto de todos los resultados posibles. Para este caso: E = øC,Xø
El Espacio de Sucesos para este caso serán: S = ø", øCø,øXø, øC,Xø ø
Verificación de un Suceso
De manera general, diremos que un suceso cualquiera A se verifica, sí al efectuar una prueba del experimento aleatorio obtenemos como resultado uno de los puntos muestrales que componen el suceso A.
Ejemplo:
Considérese el experimento que consiste en el lanzamiento de caras numeradas del 1 al 6.
Solución:
E = ø1,2,3,4,5,6ø
Sea A el suceso salir impar
A = ø1,3,5ø
El suceso A se verificará siempre que obtengamos como resultado 1,3,5 . No se verificará si se obtiene 2,4,6.
Tipos de Sucesos.
-
Sucesos Elementales:
Son aquellos que están formados por un solo punto muestral; es decir, por un solo resultado del experimento aleatorio.
-
Sucesos Compuestos:
Son aquellos que están formados por dos o más puntos muestrales; es decir, por más de un resultado del experimento.
-
Suceso Cierto:
Se llama suceso cierto o suceso seguro, al que siempre se realiza. El suceso cierto estará formado por todos los resultados posibles del experimento; es decir, coincide con el espacio muestral y también lo designaremos por la letra E.
-
Suceso Imposible:
Se llama suceso imposible a un suceso que no se realiza nunca. Se designa por ".
Ejemplo:
Considera el experimento que consiste en lanzar dos dados y sumar los resultados de las caras superiores. Determina que tipo de sucesos se pueden dar.
Solución:
Son sucesos elementales: ø2ø, ø3ø , ø4ø, ø5ø, ø6ø, ø7ø, ø8ø, ø9ø, ø10ø, ø11ø, ø12ø.
Algunos sucesos compuestos son:
A = “Sumar múltiplo de 2” B = “Sumar Número primo”
El suceso Cierto es: E = ø2,3,4,5,6,7,8,9,10,11,12ø
El suceso imposible es: "
Sucesos Contrarios.
Dado un suceso cualquiera A del espacio de sucesos S, se llama Suceso Contrario de A a un suceso que se realiza cuando no se realiza A. Se representa por A´. El suceso A´ está formado por los puntos muestrales de E que no pertenecen a A. Se verifica que
E´ = " y " = E´
Ejemplo:
Sea el experimento aleatorio que consiste en el lanzamiento de un dado, cuyo Espacio Muestral es E = { 1,2,3,4,5,6} Hallar los sucesos contrarios de los siguientes sucesos:
A = {1,2,5} A´ = {3,4,6}
B = {1,3} B´ = {2,4,5,6}
C = {4} C´ = {1,2,3,5,6}
D = {1,3,5,6} D ´= {2,4}
E = {1,2,3,4,5,6} E´ = "
F = {1,3,4,5,6} F´ = {2}
G = " G´ = E
Operaciones Con Sucesos
-
Unión de Sucesos
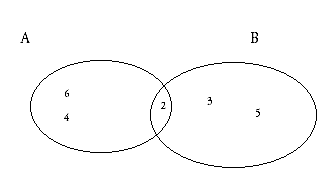
Dados dos sucesos A y B de un mismo experimento aleatorio, llamamos Suceso Unión de A y B al suceso que se realiza cuando se realiza A o B. Ser representa por A"B, este suceso estará formado por los puntos muestrales de A y B.
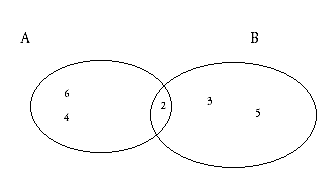
Ejemplo:
Consideremos en el experimento aleatorio del lanzamiento del dado, cuyo espacio muestral es E = {1,2,3,4,5,6} , los siguientes sucesos:
A = “Salir Número par” = {2,4,6}
B = “Salir Número Primo” = {2,3,5}
Formemos el suceso C, “salir número par o primo”. Este suceso es C = {2,3,4,5,6}
-
Intersección de Sucesos. Sucesos Incompatibles
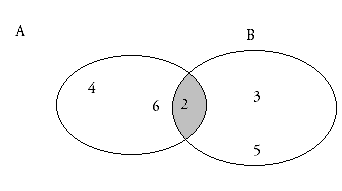
Dados dos sucesos A y B de un mismo experimento aleatorio, llamaremos Suceso Intersección de A y B al suceso que se realiza cuando se realizan simultáneamente los sucesos A y B. Se representa por A "B y está formado por los puntos muestrales comunes a los sucesos A y B.
Ejemplo:
Consideremos en el ejemplo anterior los siguientes sucesos:
A = “Salir número par” = {2,4,6}
B = “Salir Número Primo” = {2,3,5}
Formemos el suceso D, “Salir Número par y primo”. Este suceso es D = {2}
Álgebra de Boole de Sucesos
George Boole fue un matemático autodidacta inglés al que se considera hoy en día el padre de la lógica matemática.
En 1984 publicó un libro titulado The Investigation of the laws of Thought, en el que sistematiza sus ideas construyendo la lógica formal como un nuevo tipo de álgebra, esto es lo que actualmente conocemos como Álgebra de Boole.
El Álgebra de Boole es frecuentemente untilizada hoy en día no sólo por los matemáticos puros, sino por aquellas personas que la aplican al diseño de circuitos telefónicos, computadores electrónicos, cálculo de probabilidades y teoría del seguro.
Vamos a resumir de forma esquemática en qué consiste el Álgebra de Boole de sucesos.
Consideremos un experimento aleatorio cualquiera, y sean E su espacio Muestral y S el espacio de sucesos asociado. En S se definen las operaciones de Unión, Intersección y complementación (Contrario), de modo que cumplan las siguientes propiedades:
| Unión | Intersección | |
| 1. Asociativa | (A"B) " C = A " (B"C) | (A"B) " C = A " (B"C) |
| 2. Conmutativa | A"B = B"A | A"B = B"A |
| 3. Idempotente | A"A = A | A"A = A |
| 4.Simplificativa | A" (B"A) = A | |
| 5.Distributiva | A" (B"C) = (A"B) A" (B"C) = (A"B) | " (A"C) " (A"C) |
| 6. Todo suceso A del espacio de sucesos S tiene otro que llamamos contrario de A, y representamos por A´, que verifica: A"A´ = E Y A"A´ = " | ||
Definición Clásica de probabilidad
La primera definición que se conoce del concepto de probabilidad fue enunciada por Pierre Simon Laplace.
Laplace expresa, de forma sencilla, lo que entiende por cálculo de probabilidades: “ En el fondo, la teoría de probabilidades es sólo sentido común expresado con números.”
La definición de Laplace dice así:
“La probabilidad de un suceso A es el cociente entre el número de casos favorables al suceso y el número de casos posibles”
A la hora de aplicar esta definición hay que tener en cuenta que los sucesos elementales tienen que ser igualmente probables ( equiprobables).
Los casos posibles son todos los resultados del experimento, es decir, todos los elementos del espacio muestral.
Los casos Favorables son los elementos que componen el suceso A.
Ejemplo:
Se considera un experimento aleatorio que consiste en lanzar un dado.
Se pide la probabilidad de obtener un número par e impar.
Solución:
Primeramente formamos el espacio muestral del experimento: E = {1,2,3,4,5,6}
A continuación formaremos los sucesos cuya probabilidad nos piden:
A = “obtener par”
Aplicando la regla de Laplace:
B = “obtener Impar”
Aplicando la regla de Laplace:
De aquí se desprende que existe la misma probabilidad de sacar par que de sacar impar.
Definición Axiomática de Probabilidad
La construcción de una axiomática para el cálculo de probabilidades se debe al matemático ruso Andrei Nicolaievich Kolmogorov.
La idea fundamental de la axiomática de Kolmogorov es considerar la íntima relación que existe entre el concepto de frecuencia relativa de un suceso y su probabilidad, cuando el número de pruebas es muy grande.
Con el fin de que la definición de Kolmogorov nos resulte más accesible, veremos en primer lugar las propiedades de las fracuencias relativas.
1° La frecuencia relativa de un suceso cualquiera del espacio de sucesos es siempre positiva o nula:
h(a)"0
2° La frecuencia relativa del suceso cierto es igual a la unidad:
h(E) = 1
3° La frecuencia relativa de la unión de dos sucesos incompatibles es igual a la suma de las frecuencias relativas de cada uno de ellos:
Si A y B son incompatibles: h(A"B) = h(A) + h(B).
Inspirado en estas propiedades, Kolmogorov enunció la siguiente definición axiomática de probabilidad:
Se llama probabilidad a una ley que asocia a cada suceso A, del espacio de sucesos, un número real al que llamamos probabilidad de A y representamos por p(A), que cumple los siguientes axiomas:
La probabilidad de un suceso cualquiera del espacio de sucesos es positiva o nula: p(A) " 0
La probabilidad del suceso cierto es igual a la unidad: p(E) = 1
La probabilidad de la unión de dos sucesos incopatibles es igual a la suma de las probabilidades de cada uno de ellos.
Si A y B son incompatibles: p(A"B) = p(A) + p(B).
Probabilidad condicionada
Se llama probabilidad condicionada del suceso B respecto del suceso A, y la denotamos por p(B/A), al cociente siguiente:
Análogamente, la probabilidad condicionada del suceso A respecto del suceso B viene dada por la siguiente expresión:
De las dos relaciones anteriores se obtiene:
11.Probabilidad Compuesta
-
Probabilidad de la intersección de sucesos independientes
Acabamos de ver que si A y B son independientes, se verifica que . Por tanto se tiene que:
Si A y B son dos sucesos independientes, se verifica que la probabilidad de la intersección de A y B es igual al producto de las probabilidades de cada uno de ellos:
-
Probabilidad de sucesos dependientes
A partir de la definición de probabilidad condicionada se obtiene:
Si A y B son dos sucesos dependientes, se verifica que la probabilidad de la intersección de A y B es igual al producto de la probabilidad de uno de ellos, supuesta no nula, por la probabilidad del otro condicionada a la realización del anterior:
Para el caso de n sucesos la propiedad que estamos considerando se demostraría por el método de inducción. Dicha propiedad se conoce con el nombre de teorema de la Probabilidad compuesta.
Sean A1,A2,........,An, n sucesos cualesquiera de un mismo experimento aleatorio y tales que la probabilidad de la realización simultánea de los n sucesos no es nula. Se verifica entonces:
12.Teorema de la Probabilidad Total
Enunciemos de una manera general el Teorema de la Probabilidad total:
Sea A1,A2,........,An un sistema completo de sucesos tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquiera para el que se conocen laas probabilidades de p(B/Ai), entonces la probabilidad del suceso B viene dada por la siguiente expresión:
13.Teorema De Bayes
Enunciemos de una manera general este teorema:
Sea A1,A2,.....,An un sistema completo de sucesos tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquiera para el que se conocen las probabilidades p(B/A). El Teorema de Bayes establece que las probabilidades p(A/B) vienen dadas por la siguiente expresión:
-
Las probabilidades p(Ai) se denominan a priori.
-
Las probabilidades p(B/Ai) se denominan Verosimilitudes.
-
Las probabilidades p(Ai/B) se denominan a posteriori
Descargar
| Enviado por: | Javier |
| Idioma: | castellano |
| País: | España |
