Estadística
Estadística
I n d i c e
I N T R O D U C C I Ó N …………………………………………………………………………. 2
A N A L I S I S F A C T O R I A L ………………………………………………………………..3
A N A L I S I S D E C O G L O M E R A D O S J E R A R Q U I C O S ……………………7
D E S A R R O L L O D E L T R A B A J O………………………………………………………11
C O N C L U S I O N ……………………………………………………………………………….13
B I B L I O G R A F I A …………………………………………………………………………….14
Introducción
Nuestra finalidad es analizar simultáneamente conjuntos de datos multivariantes en el sentido de que hay varias variables medidas para cada individuo ú objeto estudiado.
Esto radica en un mejor entendimiento del fenómeno objeto de estudio obteniendo información que los métodos estadísticos univariantes y bivariantes son incapaces de conseguir.
Objetivos
1) Proporcionar métodos cuya finalidad es el estudio conjunto de datos multivariantes que el análisis estadístico uni y bidimensional es incapaz de conseguir.
2) Tomar decisiones óptimas en el contexto en el que se encuentre teniendo en cuenta la información disponible por el conjunto de datos analizado
En este caso utilizaremos dos Técnicas multivariantes.
1) Análisis Factorial
Se utiliza para analizar interrelaciones entre un número elevado de variables métricas explicando dichas interrelaciones en términos de un número menor de variables denominadas factores (si son inobservables) o componentes principales (si son observables).
2) Análisis Cluster
Su objetivo es clasificar una muestra de entidades (individuos o variables) en un número pequeño de grupos de forma que las observaciones pertenecientes a un grupo sean muy similares entre sí y muy disimilares del resto. A diferencia del Análisis Discriminante se desconoce el número y la composición de dichos grupos.
A N A L I S I S F A C T O R I A L
El Análisis Factorial es una modalidad del Análisis Multivariado que nos permite reducir una serie de variables a un conjunto menor (factores) que contienen la mayor parte de la información y son suficientes para explicar el método. Mediante este método se toma un gran número de variables y se investiga para ver si tiene un pequeño número de factores en común que expliquen su ínter correlación.
El Análisis Factorial de Componentes Principales analiza tablas de individuos por variables métricas, es decir este análisis se aplica a tablas rectangulares de datos, en las que columnas y filas de variables representan a los individuos.
El análisis comienza con la matriz de correlaciones, la que nos muestra los coeficientes de correlación entre cada par de variables.
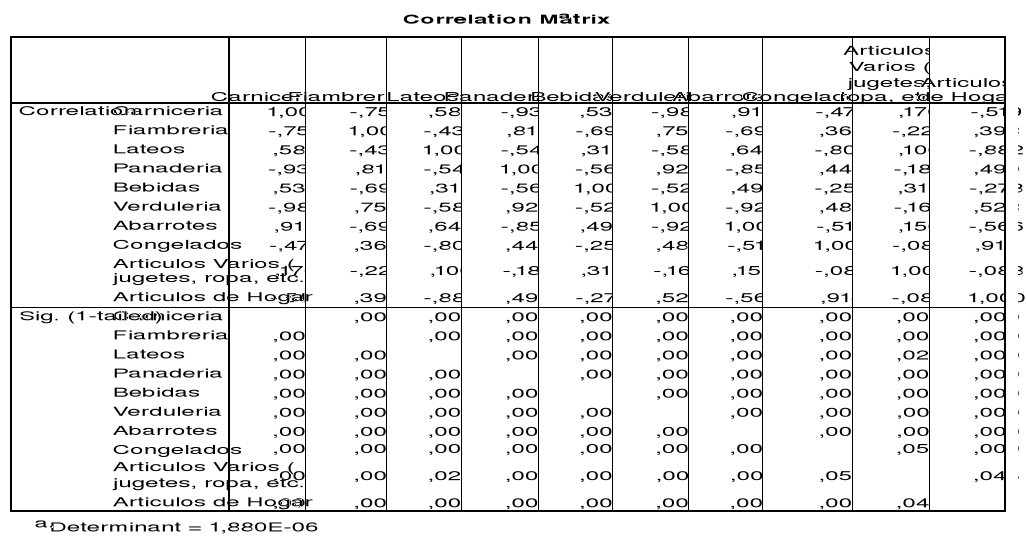
La medida de adecuación muestral de Kayser-Meyer-Olkin es un índice que nos ayuda a comparar la magnitud de los coeficientes de correlación observados con la magnitud de los coeficientes de correlación parcial.
Nuestro ejemplo posee un nivel de significancia menor que 0.05, por lo cual podemos rechazar la hipótesis nula de esfericidad, por lo tanto podemos asegurar que el modelo factorial es adecuado para explicar los datos.

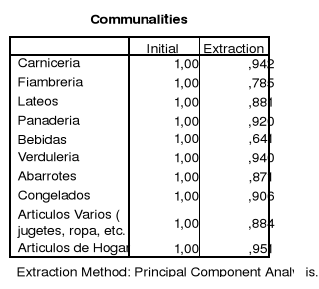
La comunalidad de una variable es la proporción de su varianza que puede ser explicada por el modelo factorial obtenido.
Por ejemplo la variable Bebidas es la peor explicada, ya que el modelo solo es capaz de reproducir el 64.1% de su variabilidad original, en contraste con el 95,1% de variabilidad que explica la variable Artículos de Hogar.
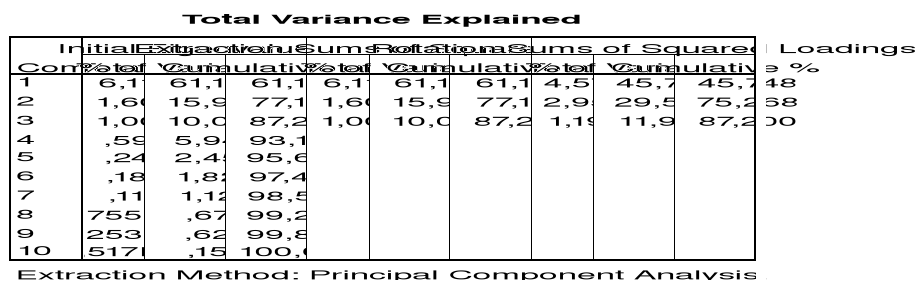
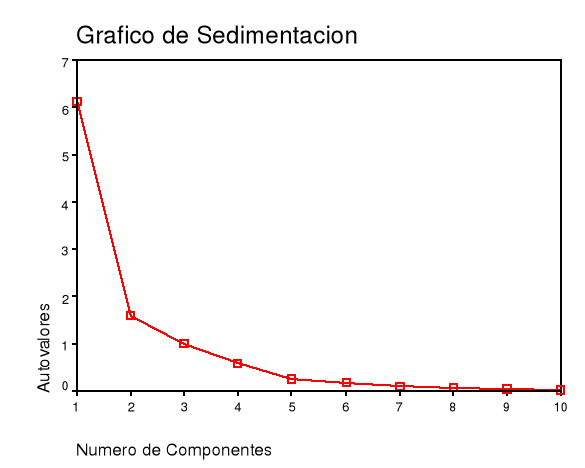
Los autovalores de la tabla siguiente expresan la cantidad de la varianza total que esta explicada por cada factor. En nuestro ejemplo hay tres autovalores mayores que uno por lo tanto el método de Componentes Principales muestra que estos tres valores explican 87.2% de varianza de datos. Esto nos ayuda a elegir el número óptimo de factores.
Esta tabla contiene las correlaciones entre las variables originales (o saturaciones) y cada uno de los factores. Comparando las saturaciones relativas de cada variable en cada uno de los tres factores podemos apreciar que la variables Congelados, y Articulas de Hogar nos hacen sospechar que no se adecuan a la solución del problema por lo cual debemos rotar la matriz.
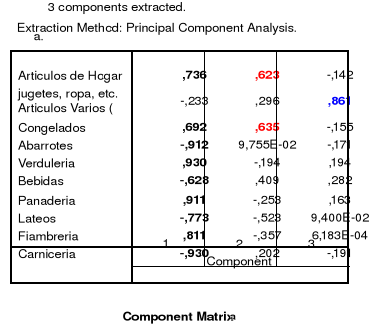
Una vez rotada la matriz vemos que las correlaciones ahora saturan, cada una, a un solo componente o factor de la matriz. Por lo cual podemos agrupar las variables de acuerdo a su relación con cada componente.
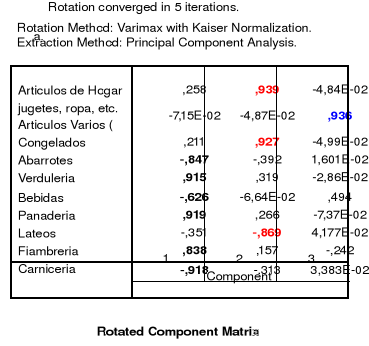
La agrupación de las variables de acuerdo a la matriz de componentes rotada y su correlación con las variables, nos quedara de la siguiente forma.
Carnicería
Fiambrería
Panadería Lácteos
C1: Bebidas C2: Congelados C3: Art. Varios
Verdulería Art. Hogar
Abarrotes
El grafico de sedimentación sirve para determinar el número óptimo de factores. Consiste simplemente en una representación grafica del tamaño de los autovalores
A N A L I S I S D E C O G L O M E R A D O S J E R A R Q U I C O S
Calculo de Distancia Euclídea Simple.
Este cálculo es una medida de similaridad utilizada por defecto para datos de intervalos, su valor mínimo es cero, pero no tiene valor máximo.
El método de vinculación simple selecciona y junta los dos elementos de la matriz de distancia que se encuentran más próximos.
La tabla de resumen nos muestra de los casos procesados, el número y porcentaje de casos validos analizados, el numero y porcentaje de casos con valores perdidos en alguna de las variables incluidas en el análisis, y el tamaño total de la muestra. El pie de página indica el nombre de la medida utilizada para obtener la matriz de distancias
La siguiente tabla nos muestra la matriz de distancia entre los 6 variables según el método de calculo de distancia euclídea simple. El cual nos indica en nuestro ejemplo que las variables más cercanas o más relacionadas son el Sexo y Nivel de vivienda.
Luego en el historial de conglomeración puede observarse que las distancias de fusión las cuales se muestran en la columna de coeficientes aumentan rápidamente conforme avanzan las etapas. Para este análisis utilizamos el método de vinculación simple (método de vinculación por el vecino más próximo) el cual comienza seleccionando los 2 elementos de la matriz de distancia que se encuentren más próximos.
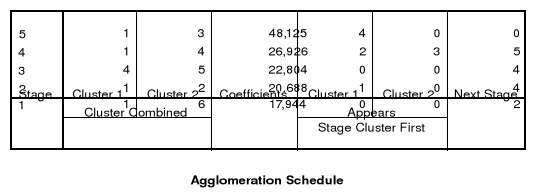
El dendrograma es un grafico que muestra el historial de conglomeración en el cual los conglomerados están representados mediante trazos horizontales, las etapas en que se juntan mediante trazos verticales. Este grafico nos ayuda a evaluar la homogeneidad de los conglomerados y nos permite decidir sobre cual es el número óptimo de conglomerados.
En nuestro caso vemos que las variables sexo y vivienda son las más próximas en el grafico de combinación de distancias representada con el corchete de color rojo más pequeño.
DENDROGRAMA
Dendrogram using Single Linkage
Rescaled Distance Cluster Combine
C A S E 0 5 10 15 20 25
Label num. +---------+---------+---------+---------+---------+
SEXO 1 ðððððð
VIVIENDA 6 ðð ððððððððððð
JF 2 ðððððð ððððððððððððððððððððððððððððððððððð
EDUC 4 ðððððððððððððððð ð
INGRESO 5 ðððððððððð ð
AD 3 ðððððððððððððððððððððððððððððððððððððððððððððððððð
Calculo de Distancia Euclídea al Cuadrado.
Este método nos dice que los conglomerados o clusters deben constituirse de tal manera que, al juntarse dos elementos, la perdida de información resultante debe ser mínima. Por lo tanto la cantidad de información se cuantifica como la suma de las distancias al cuadrado de cada elemento respecto al elemento del centro del conglomerado al que pertenece. La medida de Distancia Euclídea al cuadrado es una medida de similaridad.
El resumen de datos nos muestra los 380 casos procesados y su porcentaje, así como también podemos observar que no hay casos perdidos en ninguna de las variables.

La matriz de distancias entre los elementos procesados destaca una cercanía entre las variables sexo y nivel de vivienda; sexo y jefe de familia; nivel de educación y nivel de ingreso; por ultimo las variables nivel de educación y sexo; nivel de educación y nivel de vivienda. Siendo estas las mas relacionadas dentro de la matriz.

El historial de conglomeración de la distancia euclidea cuadrada nos muestra que las distancias aumentan rápidamente conforme avanzan las etapas. Además muestra las distancias de conglomeración y los grupos que se han ido formando al aplicar el algoritmo. El dendrograma nos muestra dicha información de forma gráfica. Así, en el primer paso se unieron Sexo y Nivel de Vivienda a una distancia igual a 161. Posteriormente se unieron las variables Nivel de Ingreso y Nivel de Educación formando otro grupo, todo ello a una distancia de aglomeración igual a 421.

DENDROGRAMA
Dendrogram using Ward Method
Rescaled Distance Cluster Combine
C A S E 0 5 10 15 20 25
Label num. +---------+---------+---------+---------+---------+
SEXO 1 ðððððð
VIVIENDA 6 ðð ððððððððððð
JF 2 ðððððð ððððððððððððððððððððððððððððððððððð
EDUC 4 ðððððððððððððððð ð
INGRESO 5 ðððð ð
AD 3 ðððððððððððððððððððððððððððððððððððððððððððððððððð
D E S A R R O L L O D E L T R A B A J O
1) El estudio y análisis del caso presentado nos muestra que es posible la aplicación de ambas técnicas multivarientes, en el caso de la tabla de las secciones mas visitadas y sus respectivas frecuencias puede ser analizado mediante un análisis factorial de componentes principales, y la segunda tabla presentada en el caso la cual se refiere a las características del consumidor pudo ser analizada mediante el análisis de conglomerados jerárquicos. Las variables de ambos problemas pueden ser agrupadas y conglomeradas en los respectivos análisis sin mayores inconvenientes.
En el caso del análisis factorial el test KMO and Bartlett vamos que el nivel de significancia es menos que 0.5 por lo cual se puede llevar a cabo el análisis sin problema sobre la explicación de las variables.
En el análisis de conglomerados jerárquicos las distintas variables pueden ser agrupadas sin la perdida de información relevante. Las variables pueden ser analizada y clasificadas en grupos mas pequeños similares entre si.
2) Bueno el Análisis Cluster es un método multivariante cuyo principal objetivo es agrupar objetos (personas, empresas, productos...) en conglomerados, de forma que cada objeto es muy parecido a los que hay en el conglomerado con respecto a algún criterio de selección predeterminado.
En el cual:
-
Los conglomerados resultantes deben mostrar un alto grado de homogeneidad interna (dentro del conglomerado) y un alto grado de heterogeneidad externa (entre conglomerados).
-
Gráficamente, los objetos dentro de los conglomerados estarán muy próximos, y los diferentes conglomerados muy alejados.
-
El análisis cluster permite la inclusión de múltiples variables para llevar a cabo la agrupación de objetos.
Mientras que el análisis factorial es un método multivariante cuyo objetivo es condensar la información contenida en un número de variables originales, en un conjunto más pequeño de variables (factores), con una mínima pérdida de información.
Es una técnica de interdependencia en la que se consideran todas las variables simultáneamente, cada una relacionada con todas las demás.
Por lo tanto el análisis cluster es comparable al factorial, pues ambos evalúan la estructura de datos. Pero mientras el factorial agrupa variables, el cluster agrupa objetos.
3) Nosotros recomendaríamos a la empresa para obtener mejor resultados, hacer el estudio teniendo en cuenta:
Segmentación de Mercados: Para identificar las variables subyacentes en las cuales deben agruparse los clientes. Así, por ejemplo, los compradores de automóviles nuevos pueden agruparse sobre la base de la importancia que dan a la economía, la comodidad, el desempeño, el lujo, el servicio postventa, etc.
Investigación de Productos: Para identificar los atributos de las marcas que influyen en la elección del consumidor. Una marca de pasta dental puede evaluarse por: la protección contra la caries, la blancura que proporciona a los dientes, el sabor, el aliento fresco que otorga, su precio, etc.
Publicidad: Para comprender los hábitos de consumo del mercado meta.
Estudios sobre Precios: Para identificar las características de los consumidores sensibles al precio. Estos consumidores pueden ser de clase media, preocupados por la economía, caseros, etc.
Para con esto poder tener una mejor información sobre los consumidores con el fin de obtener las mejores decisiones para la empresa.
4) Luego de analizar cuales son las secciones mas visitadas en el supermercado, podemos concluir que una buena solución para que las secciones menos visitadas aumenten el grupo de consumidores, es que el supermercado ordene sus secciones de tal manera que las secciones con menos frecuencia de visitantes estén cerca o de alguna manera relacionada con las secciones mas visitadas para así de esta forma cada vez que el cliente se dirija a una sección donde se encuentran los artículos de primera categoría (secciones mas visitadas), pueda ver y se sienta atraído por los artículos que se encuentras en dicha sección menos visitada.
5) Análisis Factorial.
El Análisis Factorial es una de las técnicas más complejas de la Investigación de Mercados la cual, gracias al desarrollo de la informática, puede ser aplicada actualmente con relativa facilidad. Además, brinda la posibilidad de optar entre diferentes procedimientos de acuerdo a los objetivos del estudio, lo que confiere a este análisis la posibilidad de buscar la solución más precisa, desde el punto de vista matemático y, la más elegante, desde el punto de vista estético.
El Análisis Factorial reduce la multiplicidad de pruebas y medidas hasta lograr una sencillez notable. Indica qué pruebas y medidas pertenecen al mismo grupo y cuáles miden prácticamente lo mismo. Por lo tanto, reduce el número de variables y ayuda a localizar o identificar unidades o propiedades fundamentales en que se deben basar las pruebas.
Por lo tanto podemos indicar que las seis variables consideradas inicialmente han quedado reducidas a tres factores. Se ha pasado de seis variables a tres, produciéndose la pérdida de tan sólo el 12.8 de la información original representada por las seis variables iniciales.
Análisis Cluster.
El objetivo principal del análisis cluster es definir la estructura de los datos colocando las observaciones mas parecidas en datos en conglomerados de acuerdo a las distancias obtenidas de la matriz de distancia. ) Bueno el Análisis Cluster es un método multivariante cuyo principal objetivo es agrupar objetos (personas, empresas, productos...) en conglomerados, de forma que cada objeto es muy parecido a los que hay en el conglomerado con respecto a algún criterio de selección predeterminado.
En nuestro análisis los conglomerados mostraron un alto grado de homogeneidad interna (dentro del conglomerado) y un alto grado de heterogeneidad externa (entre conglomerados).
Gráficamente, los objetos dentro de los conglomerados estarán muy próximos, y los diferentes conglomerados muy alejados.
Por lo tanto pudimos analizar las variables llevando a cabo la agrupación de estas.
CONCLUSION
Luego del análisis pudimos darnos cuenta que los métodos de análisis multivariante tanto cluster como el análisis factorial nos ayudan poder reducir la información proporcionada y así de esta manera facilitar la toma de decisiones en los estudios de los sectores de ventas mas visitados en un supermercado y las características del tipo de consumidor.
Por medio del análisis factorial pudimos darnos cuenta que se pueden identificar grupos dentro de las secciones mas visitadas. En nuestro análisis definimos aquellos grupos como artículos de primera, 2da y tercera categoría, con lo cual pudimos reducir las variables presentadas a 3 grupos de componentes.
En el análisis cluster pudimos darnos cuanta de las características de los consumidores, basada en las variables propuestas, las cuales luego del cálculo de las matrices de correlación y distancia pudimos agruparlo en 3 conglomerados, en los cuales la distancia nos indica la relación entre las variables.
Por lo tanto estos análisis nos permiten analizar más fácil mente una serie de variables agrupándolas para poder así facilitar los estudios de mercado, investigación de productos, publicidad, estudios sobre precios etc.
B I B L I O G R A F I A
-
CAPITULOS 21 Y 22 MANUAL SPSS
-
ESTADISTICAS PARA MARKETING ( PEDRO BELLIDO VASQUEZ)
-
HART CAPITULO 9 ANALISIS MULTIVARIANTE
Descargar
| Enviado por: | Daniela Munizaga |
| Idioma: | castellano |
| País: | Chile |
