Ingeniero en Informática
Arreglos
1.1 Introducción
Supongamos que nos enfrentamos a un problema como este: Una empresa que cuenta con 150 empleados, desea establecer una estadística sobre los salarios de sus empleados, y quiere saber cual es el salario promedio, y también cuantos de sus empleados gana entre $1250.00 y $2500.00.
Si tomamos la decisión de tratar este tipo de problemas con datos simples, pronto nos percataríamos del enorme desperdicio de tiempo, almacenamiento y velocidad. Es por eso que para situaciones de este tipo la mejor solución son los datos estructurados.
Un arreglo puede definirse como un grupo o una colección finita, homogénea y ordenada de elementos. Los arreglos pueden ser de los siguientes tipos:
-
De una dimensión.
-
De dos dimensiones.
-
De tres o más dimensiones.
1.2 Arreglos Unidimensionales
Un arreglo unidimensional es un tipo de datos estructurado que está formado de una colección finita y ordenada de datos del mismo tipo. Es la estructura natural para modelar listas de elementos iguales.
El tipo de acceso a los arreglos unidimensionales es el acceso directo, es decir, podemos acceder a cualquier elemento del arreglo sin tener que consultar a elementos anteriores o posteriores, esto mediante el uso de un índice para cada elemento del arreglo que nos da su posición relativa.
Para implementar arreglos unidimensionales se debe reservar espacio en memoria, y se debe proporcionar la dirección base del arreglo, la cota superior y la inferior.
REPRESENTACION EN MEMORIA
Los arreglos se representan en memoria de la forma siguiente:
x : array[1..5] of integer
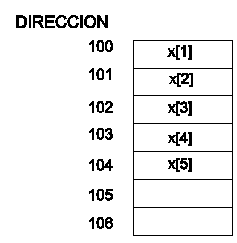
Para establecer el rango del arreglo (número total de elementos) que componen el arreglo se utiliza la siguiente formula:
RANGO = Ls - (Li+1)
donde:
ls = Límite superior del arreglo
li = Límite inferior del arreglo
Para calcular la dirección de memoria de un elemento dentro de un arreglo se usa la siguiente formula:
A[i] = base(A) + [(i-li) * w]
donde :
A = Identificador único del arreglo
i = Indice del elemento
li = Límite inferior
w = Número de bytes tipo componente
Si el arreglo en el cual estamos trabajando tiene un índice numerativo utilizaremos las siguientes fórmulas:
RANGO = ord (ls) - (ord (li)+1)
A[i] = base (A) + [ord (i) - ord (li) * w]
1.3 Arreglos Bidimensionales
Este tipo de arreglos al igual que los anteriores es un tipo de dato estructurado, finito ordenado y homogéneo. El acceso a ellos también es en forma directa por medio de un par de índices.
Los arreglos bidimensionales se usan para representar datos que pueden verse como una tabla con filas y columnas. La primera dimensión del arreglo representa las columnas, cada elemento contiene un valor y cada dimensión representa una relación
La representación en memoria se realiza de dos formas : almacenamiento por columnas o por renglones.
Para determinar el número total de elementos en un arreglo bidimensional usaremos las siguientes fórmulas:
RANGO DE RENGLONES (R1) = Ls1 - (Li1+1)
RANGO DE COLUMNAS (R2) = Ls2 - (Li2+1)
No. TOTAL DE COMPONENTES = R1 * R2
REPRESENTACION EN MEMORIA POR COLUMNAS
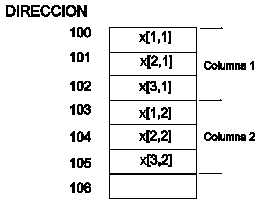
x : array [1..5,1..7] of integer
Para calcular la dirección de memoria de un elemento se usan la siguiente formula:
A[i,j] = base (A) + [((j - li2) R1 + (i + li1))*w]
REPRESENTACION EN MEMORIA POR RENGLONES
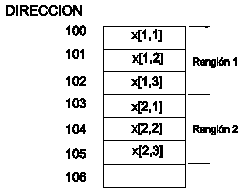
x : array [1..5,1..7] of integer
Para calcular la dirección de memoria de un elemento se usan la siguiente formula:
A[i,j] = base (A) + [((i - li1) R2 + (j + li2))*w]
donde:
i = Indice del renglón a calcular
j = Indice de la columna a calcular
li1 = Límite inferior de renglones
li2 = Límite inferior de columnas
w = Número de bytes tipo componente
1.4 Arreglos Multidimensionales
Este también es un tipo de dato estructurado, que está compuesto por n dimensiones. Para hacer referencia a cada componente del arreglo es necesario utilizar n índices, uno para cada dimensión
Para determinar el número de elementos en este tipo de arreglos se usan las siguientes fórmulas:
RANGO (Ri) = lsi - (lii + 1)
No. TOTAL DE ELEMENTOS = R1 * R2* R3 * ...* Rn
donde:
i = 1 ... n
n = No. total de dimensiones
Para determinar la dirección de memoria se usa la siguiente formula:
LOC A[i1,i2,i3,...,in] = base(A) + [(i1-li1)*R3*R4*Rn + (i2-li2)*R3*R2*... (in - lin)*Rn]*w
1.5 Operaciones Con Arreglos
Las operaciones en arreglos pueden clasificarse de la siguiente forma:
-
Lectura
-
Escritura
-
Asignación
-
Actualización
-
Ordenación
-
Búsqueda
a) LECTURA
Este proceso consiste en leer un dato de un arreglo y asignar un valor a cada uno de sus componentes.
La lectura se realiza de la siguiente manera:
para i desde 1 hasta N haz
x<--arreglo[i]
b) ESCRITURA
Consiste en asignarle un valor a cada elemento del arreglo.
La escritura se realiza de la siguiente manera:
para i desde 1 hasta N haz
arreglo[i]<--x
c) ASIGNACION
No es posible asignar directamente un valor a todo el arreglo, por lo que se realiza de la manera siguiente:
para i desde 1 hasta N haz
arreglo[i]<--algún_valor
d) ACTUALIZACION
Dentro de esta operación se encuentran las operaciones de eliminar, insertar y modificar datos. Para realizar este tipo de operaciones se debe tomar en cuenta si el arreglo está o no ordenado.
Para arreglos ordenados los algoritmos de inserción, borrado y modificación son los siguientes:
1.- Insertar.
Si i< mensaje(arreglo contrario caso En arreglo[i]<--valor i<--i+1 entonces>
2.- Borrar.
Si N>=1 entonces
inicio
i<--1
encontrado<--falso
mientras i<=n y encontrado=falso
inicio
si arreglo[i]=valor_a_borrar entonces
inicio
encontrado<--verdadero
N<--N-1
para k desde i hasta N haz
arreglo[k]<--arreglo[k-1]
fin
en caso contrario
i<--i+1
fin
fin
Si encontrado=falso entonces
mensaje (valor no encontrado)
3.- Modificar.
Si N>=1 entonces
inicio
i<--1
encontrado<--falso
mientras i<=N y encontrado=false haz
inicio
Si arreglo[i]=valor entonces
arreglo[i]<--valor_nuevo
encontrado<--verdadero
En caso contrario
i<--i+1
fin
fin
1.7 Ordenaciones en Arreglos
La importancia de mantener nuestros arreglos ordenados radica en que es mucho más rápido tener acceso a un dato en un arreglo ordenado que en uno desordenado.
Existen muchos algoritmos para la ordenación de elementos en arreglos, enseguida veremos algunos de ellos.
a)Selección Directa
Este método consiste en seleccionar el elemento más pequeño de nuestra lista para colocarlo al inicio y así excluirlo de la lista.
Para ahorrar espacio, siempre que vayamos a colocar un elemento en su posición correcta lo intercambiaremos por aquel que la esté ocupando en ese momento.
El algoritmo de selección directa es el siguiente:
i <- 1
mientras i<= N haz
min <-i
j <- i + 1
mientras j <= N haz
si arreglo[j] < [min] entonces
min <-j
j <- j + 1
intercambia(arreglo[min],arreglo[i])
i <- i +1
b)Ordenación por Burbuja
Es el método de ordenación más utilizado por su fácil comprensión y programación, pero es importante señalar que es el más ineficiente de todos los métodos .
Este método consiste en llevar los elementos menores a la izquierda del arreglo ó los mayores a la derecha del mismo. La idea básica del algoritmo es comparar pares de elementos adyacentes e intercambiarlos entre sí hasta que todos se encuentren ordenados.
i <- 1
mientras i < N haz
j <- N
mientras j > i haz
si arreglo[j] < arreglo[j-1] entonces
intercambia(arreglo[j],arreglo[j-1])
j < j - 1
i <- i +1
c)Ordenación por Mezcla
Este algoritmo consiste en partir el arreglo por la mitad, ordenar la mitad izquierda, ordenar la mitad derecha y mezclar las dos mitades ordenadas en un array ordenado. Este último paso consiste en ir comparando pares sucesivos de elementos (uno de cada mitad) y poniendo el valor más pequeño en el siguiente hueco.
procedimiento mezclar(dat,izqp,izqu,derp,deru)
inicio
izqa <- izqp
dera <- derp
ind <- izqp
mientras (izqa <= izqu) y (dera <= deru) haz
si arreglo[izqa] < dat[dera] entonces
temporal[ind] <- arreglo[izqa]
izqa <- izqa + 1
en caso contrario
temporal[ind] <- arreglo[dera]
dera <- dera + 1
ind <- ind +1
mientras izqa <= izqu haz
temporal[ind] <- arreglo[izqa]
izqa <- izqa + 1
ind <- ind +1
mientras dera <= deru haz
temporal[ind] <=dat[dera]
dera <- dera + 1
ind <- ind + 1
para ind <- izqp hasta deru haz
arreglo[ind] <- temporal[ind]
fin
1.8 Búsquedas en Arreglos
Una búsqueda es el proceso mediante el cual podemos localizar un elemento con un valor especifico dentro de un conjunto de datos. Terminamos con éxito la búsqueda cuando el elemento es encontrado.
A continuación veremos algunos de los algoritmos de búsqueda que existen.
a)Búsqueda Secuencial
A este método tambien se le conoce como búsqueda lineal y consiste en empezar al inicio del conjunto de elementos , e ir atravez de ellos hasta encontrar el elemento indicado ó hasta llegar al final de arreglo.
Este es el método de búsqueda más lento, pero si nuestro arreglo se encuentra completamente desordenado es el único que nos podrá ayudar a encontrar el dato que buscamos.
ind <- 1
encontrado <- falso
mientras no encontrado y ind < N haz
si arreglo[ind] = valor_buscado entonces
encontrado <- verdadero
en caso contrario
ind <- ind +1
b)Búsqueda Binaria
Las condiciones que debe cumplir el arreglo para poder usar búsqueda binaria son que el arreglo este ordenado y que se conozca el numero de elementos.
Este método consiste en lo siguiente: comparar el elemento buscado con el elemento situado en la mitad del arreglo, si tenemos suerte y los dos valores coinciden, en ese momento la búsqueda termina. Pero como existe un alto porcentaje de que esto no ocurra, repetiremos los pasos anteriores en la mitad inferior del arreglo si el elemento que buscamos resulto menor que el de la mitad del arreglo, o en la mitad superior si el elemento buscado fue mayor.
La búsqueda termina cuando encontramos el elemento o cuando el tamaño del arreglo a examinar sea cero.
encontrado <- falso
primero <- 1
ultimo <- N
mientras primero <= ultimo y no encontrado haz
mitad <- (primero + ultimo)/2
si arreglo[mitad] = valor_buscado entonces
encntrado <- verdadero
en caso contrario
si arreglo[mitad] > valor_buscado entonces
ultimo <- mitad - 1
en caso contrario
primero <- mitad + 1
c)Búsqueda por Hash
La idea principal de este método consiste en aplicar una función que traduce el valor del elemento buscado en un rango de direcciones relativas. Una desventaja importante de este método es que puede ocasionar colisiones.
funcion hash (valor_buscado)
inicio
hash <- valor_buscado mod numero_primo
fin
inicio <- hash (valor)
il <- inicio
encontrado <- falso
repite
si arreglo[il] = valor entonces
encontrado <- verdadero
en caso contrario
il <- (il +1) mod N
hasta encontrado o il = inicio
Descargar
| Enviado por: | Gladiador |
| Idioma: | castellano |
| País: | Venezuela |
