Matemáticas
Álgebra
INDICE.
ALGORITMO DE LA DIVISIÓN....................................................3
NUMEROS PRIMOS.....................................................................5
CRIBA DE ERATOSTENES.........................................................8
FACTORIZACION DE UN NUMERO.........................................10
MÁXIMO COMUN DIVISOR.......................................................11
MÁXIMO COMUN MÚLTIPLO...................................................12
ALGORITMO DE EUCLIDES.....................................................12
CONCLUSIONES.......................................................................14
ALGORITMO DE LA DIVISIÓN.
Comenzaremos esta sección estudiando el algoritmo de la división que establece el siguiente teorema:
Teorema 1.4. [Algoritmo de la división] Si a y b son enteros con b > 0, existe un único par de enteros q y r tales que
![]()
Demostración:
Existencia: Sea ![]()
. Este conjunto de enteros contiene elementos no negativos (por ejemplo, para n = - | a | ), por lo que S*= S ![]()
N es un subconjunto no vacío de N y, por tanto, de Z . El axioma de buena ordenación de los números enteros nos asegura la existencia de un primer elemento de S* que será de la forma r = a - qb ![]()
0 para algún entero q. Se tiene, por tanto, que a = qb+r con r ![]()
0. Si r ![]()
b, S* contendría al elemento no negativo a - (q+1)b = r - b < r que contradice el hecho de que r es el primer elemento del conjunto S*. Por tanto, r < b.
Unicidad: Supongamos que existen dos parejas de enteros (q, r) y (q', r') tales que
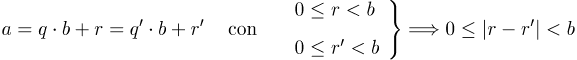
Se tiene entonces que
![]()
lo que imposibilita el hecho de que | r - r' | < b. Por tanto, ha de ser q = q' y de ahí que también sea r = r', lo que prueba la unicidad.
Definición 1.5. Con la notación del Teorema 1.4 el entero q recibe el nombre de cociente entero o simplemente cociente y el también entero r el de resto. Si dividimos por b obtenemos que a / b = q+ r / b con 0![]()
r / b < 1 por lo que q viene dado por la parte entera por defecto o suelo de a / b (el mayor entero i con i![]()
a / b) y que denotaremos por ![]()
. Esto facilita el cálculo de q. El de r se realiza posteriormente mediante la igualdad r = a - qb.
Si consideramos ahora el caso b < 0, dado que -b > 0, el Teorema 1.4 nos garantiza la existencia de los enteros q* y r tales que a = q* (-b) + r con 0 ![]()
r < - b, y haciendo q* = - q se obtiene que a= qb+ r. La prueba de la unicidad es similar a la anterior.
Teniendo en cuenta este resultado y el del Teorema 1.4, podemos establecer el siguiente corolario:
Corolario 1.6. Si a y b son dos enteros con b ![]()
0, existe un único par de enteros q y r tales que
![]()
Obsérvese que si b < 0 se tiene que a / b = q + r / b con 0 ![]()
r / b > -1 por lo que en este caso q es la parte entera por exceso o techo del cociente a / b que denotaremos por ![]()
, es decir, el menor entero i tal que i ![]()
a / b.
Definición 1.7. Si a y b son enteros y a= qb para algún entero q, diremos que b divide a a, o bien que b es un factor o un divisor de a, o también que a es múltiplo de b.
Así, por ejemplo, los factores de 6 son ±1, ±2, ±3 y ±6. Cuando b divide a a lo denotaremos por b | a. Para evitar errores obsérvese que cualquier entero divide a 0 (ya que 0 = 0 · b para cualquiera que sea el entero b), 1 divide a cualquier entero y cualquier entero se divide a si mismo. Debido a ello, dado un entero n, sólo los divisores de n distintos de 1 y del propio n se consideran divisores propios de dicho número.
Recordamos a continuación algunas propiedades simples pero útiles de la divisibilidad, probando dos de ellas y dejando la demostración de las otras a modo de ejercicios para el alumno.
Teorema 1.8. Se verifican las siguientes propiedades:
a | b y b | c ![]()
a | c.
a | b y c | d ![]()
ac | bd.
Si m ![]()
0 ![]()
a | b si, y sólo si, ma | mb.
Si a ![]()
0 y d | a ![]()
| d |![]()
| a |.
Si c | a1, . . . , ak ![]()
c | a1u1+ ![]()
+ akuk cualesquiera que sean los enteros u1, . . . , uk.
a | b y b | a si, y sólo si, a = ± b.
Demostración: (Se demostrarán aquí, solamente las propiedades 5 y 6).
Si c | ai se tiene que ai = qi c para algunos enteros qi (i=1,2, . . . , k). Entonces
a1u1+ ![]()
+akuk= q1cu1+ ![]()
+ qkcuk = (q1u1 + ![]()
+ qkuk) c
y dado que q1u1+ ![]()
+qkuk ![]()
Z , se tiene que c | (a1u1+ ![]()
+ akuk).
Si a = ± b se tiene que b = qa y a = q'b donde q = q' = ± 1, por lo que a | b y b | a.
Recíprocamente, si a | b y b | a es b = qa y a = q'b para algunos enteros q y q'. Si b = 0, de la segunda igualdad se obtiene que a = 0, por lo que a = ± b. Podemos suponer, por tanto, que b ![]()
0. Eliminando a de ambas expresiones, obtenemos que b = qq'b y como b no es nulo, por la propiedad cancelativa podemos asegurar que qq' = 1, por lo que q = q' = 1 y, por tanto, a = ± b.
La forma más usual del Teorema 1.8. (5) es el caso k = 2, que recordamos a continuación con una notación más simple.
Corolario 1.9. Si c es un divisor de a y de b, divide a au+bv cualesquiera que sean los enteros u y v.
NUMEROS PRIMOS.
Una de las cuestiones básicas en la teoría de números es la cuestión de la divisibilidad de un número por otro. Los números enteros que sólo son divisibles por 1 y por si mismos, se llaman números primos.
El número de números primos es infinito. El primero que lo demostró fue Euclides, en el Libro IX de Elementos, después lo demostraron Euler y Chebichev. La demostración es muy sencilla: Supongamos que tenemos un conjunto {p1, p2, p3, ...} que incluye todos los números primos. Calculemos el número N = p1.p2.p3 ... + 1. Evidentemente este número es primo porque no es divisible por ninguno de los números primos que hemos considerado. Por lo tanto, el conjunto del que hemos partido no incluye todos los números primos.
Los números primos son, en cierto modo, como los elementos químicos. A partir de los elementos químicos se forman todos los compuestos químicos y a partir de los números primos podemos obtener el resto de los números.
Sería fantástico que hubiese una fórmula que produjese números primos. Hasta 1536 se pensó que los números de la forma 2n-1 eran todos primos, pero ese año Hudalricus Regius, demostró que 211 - 1 = 2047 era el producto de 23 y 89. Sin embargo, muchos (se supone que infinitos) números primos cumplen esa condición. A los números primos que cumplen esa condición se les llama números primos de Mersenne (Marin Mersenne (1588-1648) fue un monje francés, muy famoso en su época). Mersenne en su libro Cogitata Physica-Mathematica dijo que los números de la forma 2n - 1 eran primos para n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 y 257 y compuestos para los restantes números < 257.
Euler en 1750 lo demostró para n = 31, Lucas, en 1876 lo demostró para n = 127. Años mas tarde Pervouchine encontró que también era primo el número para n = 61 y en 1900 Powers descubrió que también lo eran para n = 89 y n = 107.
Los números primos de Mersenne y los números perfectos están relacionados. Los números primos de Mersenne son de la forma 2n - 1 y los perfectos son de la forma 2n - 1(2n - 1).
Hasta hoy (11-07-99) se han descubierto 38 números de Mersenne, el último es 26972593 - 1 descubierto por el GIMPS (Great Internet Mersenne Prime Search).
| Tabla de números primos de Mersenne conocidos | |||
| Número de orden | Exponente | Año descubrimiento | Descubridor |
| 1 | 2 |
|
|
| 2 | 3 |
|
|
| 3 | 5 |
|
|
| 4 | 7 |
|
|
| 5 | 13 | 1456 | Anónimo |
| 6 | 17 | 1588 | Cataldi |
| 7 | 19 | 1588 | Cataldi |
| 8 | 31 | 1772 | Euler |
| 9 | 61 | 1883 | Pervushin |
| 10 | 89 | 1911 | Powers |
| 11 | 107 | 1914 | Powers |
| 12 | 127 | 1876 | Lucas |
| 13 | 521 | 1952 | Robinson |
| 14 | 607 | 1952 | Robinson |
| 15 | 1279 | 1952 | Robinson |
| 16 | 2203 | 1952 | Robinson |
| 17 | 2281 | 1952 | Robinson |
| 18 | 3217 | 1937 | Riesel |
| 19 | 4253 | 1961 | Hurwitz |
| 20 | 4423 | 1961 | Hurwitz |
| 21 | 9689 | 1963 | Gillies |
| 22 | 9941 | 1963 | Gillies |
| 23 | 11213 | 1963 | Gillies |
| 24 | 19937 | 1971 | Tickerman |
| 25 | 21701 | 1978 | Noll y Nickel |
| 26 | 23209 | 1979 | Noll |
| 27 | 44497 | 1979 | Nelson y Slowinski |
| 28 | 86243 | 1982 | Slowinski |
| 29 | 110503 | 1988 | Colquitt y Welsh |
| 30 | 132049 | 1983 | Slowinski |
| 31 | 216091 | 1985 | Slowinski |
| 32 | 756839 | 1992 | Slowinski y Gage |
| 33 | 859433 | 1994 | Slowinski y Gage |
| 34 | 1257787 | 1996 | Slowinski y Gage |
| 35 | 1398269 | 1996 | GIMPS |
| 36 | 2976221 | 1997 | GIMPS |
| 37 | 3021377 | 1998 | GIMPS |
| 38 | 6972593 | 1999 | GIMPS |
Pierre de Fermat (1601-1665) creyó haber encontrado una fórmula que producía números primos Fi = 2n + 1 siendo n = 2i , esta fórmula genera números primos para i = 0, 1, 2, 3 y 4. Leonhard Euler (1707-1783) descubrió que F5 no es primo, en 1880 se demostró que F6 tampoco lo es, en 1970 se demostró que tampoco lo era F7, en 1980 se demostró para F8 y en 1990 para F9.
Algunos números primos están separados sólo por un número par (p.e. el 3 y el 5). A estos números se les llama números primos gemelos. Por lo tanto la cantidad mínima de números entre dos números primos es uno. ¿Cuál será la cantidad máxima? La respuesta es la que queramos: Si nos piden construir 1000 números consecutivos que no sean primos, sólo tenemos que hacer la siguiente operación: 1001! + 2, 1001! + 3, 1001! + 4,... 1001! + 1001.
Sólo hay tres números primos contiguos: 3, 5 y 7.
Se dice que dos números son primos entre sí (también se llaman primos relativos) cuando no son divisibles entre si (dicho más matemáticamente, cuando el máximo común divisor de dichos números es 1). Ejemplo, los números 38 y 14 son primos entre sí.
Dado un número a, se llama conjunto reducido de restos, al conjunto de números menores que a, que son primos entre sí con el número a. Ejemplo: el conjunto reducido de restos de 14 es {1,3,4,5,6,8,9,10,11,12,13}.
CRIBA DE ERATOSTENES.
Desde los tiempos de los antiguos griegos, los números primos han demostrado ser tanto fascinantes como evasivos. En toda la historia, los matemáticos han buscado distintas formas de encontrarlos, pero el único método realmente exitoso descubierto hasta ahora es el del matemático y astrónomo Eratóstenes de Alejandría. ¡ Y esto fue hace cerca de 2000 años !.
Se menciona que el número primo mas grande que se conoce está formado de 25962 cifras y se escribe en la forma 286243 -1. Para que te des una idea de que tan grande es este número resuelve la potenciacion de 210. Sin embargo, los antiguos griegos demostraon que nunca se encontrara el primo mayor a todos los demás. Por eso hicieron la siguiente demostración.
Imagina que hay un número primo mas grande que todos los demás llamado P, multiplica todos los numeros primos juntos, incluyendo a P: y sumale al resultado 1.
2x3x5x7x11x13x17x19x....x P.
El nuevo resultado no será divisible entre ninguno de los números primos usados para obtenerlo. ¿Por Qué? Esto significa que este nuevo número también es primo ( o bién, que tiene un factor primo mayor que P), pero esto es una contradicción puesto que dijimos que P era el primo más grande, la contradicción muestra que nuestra primera idea era incorrecta, por lo que no puede haber un primo mayor que los demás.
Alguna vez se pensó que la fórmula siguiente era una forma de encontrar números primos:
n2 - n + 41 = P
n2 = cualquier número multiplicado por si mismo.
n = se resta el número original.
41 = se suma 41
P = El resultado es igual a un número primo
Ejemplo:
22 - 2 + 41 = 43
por lo tanto el número 43 es un número primo.
Aunque funciona con algunos números enteros, falla cuando n=41. Intentalo
Aun con la ayuda de computadoras modernas, la tarea de hallar números primos cada vez mas grandes es lenta. Aun cuando se puede eliminar todos los números pares, así como todos los números que terminan en 5, cualquiera de los demás números impares tiene las características necesarias para ser primo y por ello debe ser sometido a prueba.
La búsqueda de modelos en una serie de números es una experiencia muy satisfactoria para los matemáticos, ellos pueden usar los modelos para predecir y probar demostraciones y formulas. Uno de los aspectos que ha fascinado a los matematicos acerca de los numeros primos en la forma en que se resisten a caer en algún modelo reconocible. La única forma de saber si un número es primo o no, es usando el filtro laborioso de la CRIBA DE ERATOSTENES.
Por tal motivo los números naturales se clasifican en tres grupo:
a) Números Primos: Son aquellos que tienen unicamente 2 divisores, la unidad y el mismo.
b) Números Compuestos: Es aquel que tiene mas de 2 divisores.
c) Elemento Unitario: Al número 1 se le llama elemento unitario, por lo tanto no es numero primo, por que solo tiene un divisor que es el mismo.
Existe una cantidad infinita de números primos. Esto quiere decir que frente a un número primo cualquiera, siempre habrá otro número primo mayor.
En general el matemático Griego Eratóstenes ideó un método para encontrar números primos. Este procedimiento se le conoce como Criba de Eratóstenes, para encontrar los números primos menores que 100, se procede de la siguiente manera.
1.- Se escriben todos los números naturales del 1 al 100.
2.- Se encierra el 1 en un rombo por sel el ELEMENTO UNITARIO.
3.- El siguiente número sin encerrar, es el número 2, por lo tanto es número primo. Este se encierra en un cuadrado.
4.- Se encierran en un circulo todos los multiplos de 2 mayores que 2.
5.- El siguiente número sin encerrar es el número 3, por lo tanto es un número primo, este se encierra en un cuadrado.
6.- En seguida se encierran en un circulo todos los multiplos de 3 mayores que 3.
7.- El siguiente número sin encerra es el número 5, por lo tanto es un número primo, este se encierra en un cuadrado.
8.- A continuación se encierran en un circulo todos los multiplos de 5 mayores que 5.
9.- El siguiente número sin encerrar es el número 7, por lo tanto es un número primo, este se encierra en un cuadrado.
10.- Luego, se encierran en un circulo todos los multiplos de 7 mayores que 7.
11.- El siguiente número sin encerrar es el número 11, por lo tanto es un número primo, este se encierra en un cuadrado.
12.- Todos los multiplos de 11 ya están encerrados. Por último se deben encerrar en un cuadrado todos los numeros que no esten encerrados en un circulo.
FACTORIZACION DE UN NUMERO.

La factorización de los números naturales consiste en descomponer un número entero cualquiera en producto de números primos.
La descomposición de los números de su factores primos facilita la determinación de su m.c.d. y m.c.m. Ejemplo:

Una vez realizada la factorización hemos calculado el máximo común divisor (m.c.d.) y el mínimo común múltiplo (m.c.m.).
El m.c.d. es aquel número mayor y común que divide a todos ellos.
El m.c.m. es aquel número menor y común que es múltiplo a todos ellos.
Para calcular el m.c.d. se toman los factores comunes con el menor exponente y se multiplican.
Para calcular el m.c.m. se toman los factores comunes y no comunes con el mayor exponente y se multiplican. (La solución del m.c.d. y del m.c.m. está realizado en el ejemplo de arriba).
MÁXIMO COMUN DIVISOR.
Decimos que d es un divisor común (o factor común) de a y b; por ejemplo, 1 es un divisor común a cualquier par de enteros a y b. Si a y b son no nulos, el máximo común divisor de a y b que denotaremos por mcd(a,b); siendo el único entero d que satisface
d | a y d | b (por ser d un divisor común),
Si c | a y c | b ![]()
c | d (pues d es el mayor de los divisores comunes de a y b).
Sin embargo, el caso a = b = 0 debe ser excluido; cualquier entero divide a 0 y es, por tanto, un divisor común de a y b, por lo que, en este caso, no existe un máximo común divisor. Esta definición puede obviamente extenderse al máximo común divisor de cualquier conjunto de enteros (no todos nulos).
MINIMO COMUN MÚLTIPLO.
Si a y b son dos enteros, un múltiplo común de a y b es un entero c tal que a | c y b | c. Si a y b son ambos no nulos, existen múltiplos comunes positivos (por ejemplo | ab |), por lo que el axioma de buena ordenación nos asegura la existencia de un mínimo común múltiplo, o más concretamente, el menor múltiplo común positivo. Este es el único entero positivo m que cumple:
a | m y b | m (ya que m es un múltiplo común),
a | c y b | c con c > 0 ![]()
m ![]()
c (ya que ningún múltiplo común puede ser menor que m).
Usualmente se denota a m como mcm(a,b). Las propiedades del mínimo común múltiplo pueden deducirse a partir de las del máximo común divisor a través del siguiente resultado.
(Como mcd(a,b) = mcd( | a | , | b | ) y mcm(a,b) = mcm( | a | , | b | ), no supone restricción alguna el suponer a , b > 0).
Demostración: Sean a' = a/d y b' = b/d y consideremos ab/d = (da' db') / d = da'b'. Evidentemente da'b' es positivo, por lo que debemos probar que es igual a m probando que satisface las dos condiciones de la definición de mcm(a,b).
En primer lugar, da'b' = (da')b' = ab' y da'b' = (db')a' = ba'; por lo que a | da'b' y b | da'b', es decir, se satisface la primera de las condiciones.
En segundo lugar, supongamos que a | c y b | c con c > 0; debemos probar que da'b' ![]()
6 c. Por la identidad de Bezout existen enteros u y v tales que d= au+bv. Entonces

ALGORITMO DE EUCLIDES.
el Algoritmo de Euclides que es un método muy astuto para calcular el divisor común entre dos números. Una de sus principales ventajas es que es necesario calcular los divisores ni los factores de los números, por lo que anda muy muy rápido, incluso cuando alguno de los números es un primo o tiene algún factor primo grande.
Este método se basa en la siguiente propiedad:
-
si A y B son enteros entonces DCM(A,B) = DCM(A-B,B)
La idea es ir achicando los números tanto como se pueda hasta que el DCM sea obvio, por ejemplo que sean ambos números iguales, o que uno de los dos sea cero.
Por ejemplo: para calcular el DCM(8069,5209)
DCM(8069,5209) =DCM(8069-5209,5209) =DCM(2860,5209) =DCM(5209-2860,2860) =DCM(2349,2860) =DCM(2860-2349,2349) =DCM(511,2349) =DCM(2349-511,511) =DCM(1838,511) =DCM(1838-511,511) =DCM(1327,511) =DCM(1327-511,511) =DCM(816,511) =DCM(816-511,511) =DCM(305,511) =DCM(511-305,305) =DCM(206,305) =DCM(305-206,206) =DCM(99,206) =DCM(206-99,99) =DCM(107,99) =DCM(107-99,99) =DCM(8,99) =DCM(99-8,8) =DCM(91,8) =DCM(91-8,8) =DCM(83,8) =DCM(83-8,8) =DCM(75,8) =DCM(75-8,8) =DCM(67,8) =DCM(67-8,8) =DCM(59,8) =DCM(59-8,8) =DCM(51,8) =DCM(51-8,8) =DCM(43,8) =DCM(43-8,8) =DCM(35,8) =DCM(35-8,8) =DCM(27,8) =DCM(27-8,8) =DCM(19,8) =DCM(19-8,8) =DCM(11,8) =DCM(11-8,8) =DCM(3,8) =DCM(8-3,3) =DCM(5,3) =DCM(5-3,3) =DCM(2,3) =DCM(3-2,2) =DCM(1,2)= DCM(2-1,1) =DCM(1,1) =DCM(1-1,1) =DCM(0,1) =1
Si revisan con cuidado, van a ver que a pesar de que son muchas cuentas, todas son muy simples (solo hay que restar y restar y restar). En cambio si uno trata de calcular el divisor común mayor de la manera usual, puede pasarse bastante tiempo buscando cuales son los divisores de 8069 y 5209.
CONCLUSIONES.
-
Yo creo que los números primos son una parte importante en las matemáticas ya que muchas operaciones básicas como las que vimos anteriormente dependen de ellos
-
Las matemáticas podrán parecer muy difíciles pero uno las tiene que aprender ya que son una parte importante en nuestras vidas, y no hay profesión que no necesites de ellas.
-
Gracias a gente como Euclides y los grandes matemáticos, las enseñanzas que han dejado a través de los años han hecho que hoy en día se hayan hecho muchos avances en la ciencia como son las computadoras, pero no solo las computadoras sino también, el hombre no hubiera podido llegar al espacio sin ellas o tener la tecnología que tenemos hoy en día.
-
Para facilitar la vida de las matemáticas existe la factorización de la cual sacamos el mínimo común múltiplo y el máximo común divisor qque ayuda a hacer de las matemáticas una ciencia mas fácil de responder.
-
Yo creo que todo los que nos rodea tiene una razón de ser y todo se puede responder gracias a las matemáticas.
Descargar
| Enviado por: | Al-nahum |
| Idioma: | castellano |
| País: | México |
