Tecnología
Volumen. Masa y densidad
Tarea N°1
Transferencia de materia
Problema:
Determine el volumen del estanque requerido para disolver 8 ton/h de Na2CO3 en una solución de 15% de NaCl en un estanque agitado a 30C que opera a 80% saturación. Si la granulometria es: 20% -75+100; 60% -100+200; 20% -200.
Balances de materia:
Balance Global: F + E = S
Balance por componente: E = S * XNa2CO3
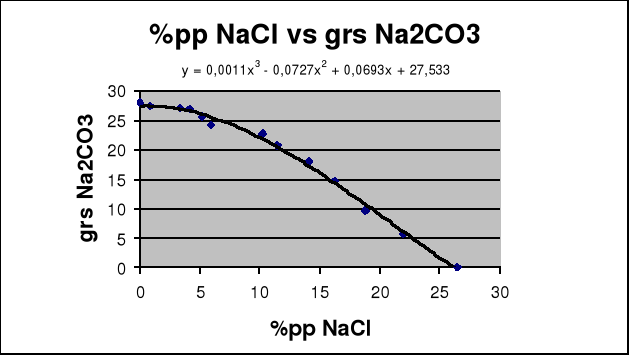
Desde los datos proporcionados por Cocheret, 1911, acerca de la solubilidad del carbonato de sodio en una solucion acuosa de cloruro de sodio, tenemos el siguiente grafico.
(fuente: )
En él, se expresa una regresión cubica que representa de mejor manera el comportamiento de los datos
15.93 g Na2CO3/100 g soluc. NaCl
Así, la solubilidad del Na2CO3 en una solución de NaCl al 15% es de 15,93 g de Na2CO3 por cada 100 g de solución saturada a 30° C.
15.93 g Na2CO3 100% sat.
x 80% sat.
x = 12.74 g Na2CO3
Entonces para una solución 80% de saturación de Na2CO3, se debe tener:
112.4 g Na2CO3 100%
12.74 g XNa2CO3
XNa2CO3 = 0.113 = 11.30%
Entonces, del balance por componente obtenemos:
E = S * XNa2CO3 ; XNa2CO3 = 0.113, E = 8 ton/h Na2CO3
8 ton/h Na2CO3 = S * 0.113
S = 70.8 ton/h
Y del balance global tenemos:
F + E = S ; E = 8 ton/h, S = 70.8 ton/h
F = E - S = 70.8 ton/h - 8 ton/h
F = 62.8 ton/h soluc. 15% NaCl
El balance para una partícula que intercambia materia con su medio queda expresado por:
-dm = Apartícula * PM * kc * (Cwi - Cw) * dt
m = ρ * V
m = ρ ð ððð ð (Dp)3 ; así
dm = 3 * ρ ð ððð ð (Dp)2 dDp ; finalmente
-ρ ð dDp = 2 * PM * kc * ðC * dt ; ðC = Cwi - Cw
donde:
dm : Diferencial de masa
Apartícula : Area de la partícula
PM : Peso molecular de Na2CO3 = 106 g/mol
Kc : Coeficiente de transferencia de masa
Cwi : Concentración en la interfase = 0.176 g/cm3 = 1.66x10-3 mol/cm3
Cw : Concentración en el seno del fluido = 0.141 g/cm3 = 1.33x10-4 mol/cm3
Dt : Diferencial de tiempo
ρ ð Densidad de la partícula = 1.972 g/cm3
Dp : Diámetro de la partícula = 0.0196 cm
ðC : Diferencia de concentración = 3.3x10-4 mol/cm3
Según granulometria entregada, y según tabla ISO tenemos como diámetro de partículas:
-75+100 : 196 ðm : 0.0196 cm
-100+200 : 160 ðm : 0.0160 cm
-200 : 76 ðm : 0.0076 cm
según estos datos tomamos para la integral el diámetro de la partícula mas grande, ya que así nos aseguramos que en el tiempo que dicha partícula se encuentre dentro del estanque de agitación, la partícula de Na2CO3 se disuelva. Obtenemos entonces:
-1.972 g/cm3 * -0.0196 cm = 2 * 106 g/mol * kc * 3.3x10-4 mol/cm3 * t
0.0386 = 0.076 * kc * t
t = 0.55/kc
Entonces para encontrar el valor de t, necesitamos el coeficiente de transferencia de materia kc.
Para ello, utilizaremos el gráfico a continuación al cual entramos con los valores de:
(ð *Dp4ððð)1/3 y (kc*Dp/DAB)*Sc-1/3
donde:
ð : Potencia del agitador en erg/s
DAB : Difusividad del Na2CO3 = 9.23 x10-6 cm2/s
ð : Viscosidad cinemática = ððρNaCl ð (8.007x10-3 g/cm*s) /1.1085 g ð 0,0072 cm2/s
ð : Viscosidad
ρNaCl : Densidad solución NaCl 15%
Nos damos una potencia de 0.25 hp/m3, entonces para un Vinicial de iteración de 60.650 m3, correspondientes al volumen para una base de calculo de una hora, tenemos
ð = 0.25 hp/m3 * 60 m3 = 15 hp = 11185.5 watt
= 1.12 x1011 erg/s
(ð *Dp4ððð)1/3 = 6.337
(kc*Dp/DAB)*Sc-1/3 = 1.8 (valor desde el gráfico)
Se expone a continuación la iteración realizada en EXCELtm
| e (erg/s*g) | dp (cm) | D (cm) | Sc | S cm3/s | dens sol. Na2co3 (g/cm3) | v (cm2/s) |
| 1,12E+11 | 0 | 9,23E-06 | 518 | 10897,20 | 1,952 | 7,20E-03 |
| V (cm3) | m (g) | (e*dp4/v3)1/3 | de grafico | kc | t=0,55/kc | V=t*S |
| 6,07E+07 | ||||||
| 6,07E+07 | 118388800 | 6,337 | 1,8 | 0,0075 | 73,372 | 799552,1967 |
| 8,00E+05 | 1560726 | 26,824 | 3,8 | 0,0158 | 34,755 | 378735,2511 |
| 3,79E+05 | 739291 | 34,411 | 4,2 | 0,0175 | 31,445 | 342665,2272 |
| 3,43E+05 | 668883 | 35,578 | 4,3 | 0,0179 | 30,714 | 334696,2684 |
| 3,35E+05 | 653327 | 35,858 | 4,35 | 0,0181 | 30,361 | 330849,1849 |
Donde encontramos una diferencia poco importante para un volumen V = 330849.2 cm3, para t =30 s.
Sin embargo siendo consecuentes que el volumen de entrada a esta iteración fue tomado para un tiempo de 1 hora , tenemos:
t = 1 h = 3600 s ; V = 39.7 m3 ~= 40 m3
diseñando, tenemos:
V = Abasal* H = ð * D2/4 * H
Por diseño tomamos la relación H = 1.2 * D ;que equivale a entregar a la altura el 20% de la longitud del diámetro, evitamos así, el derramamiento de fluido del estanque por la agitación.
Entonces.
V = ð * D2/4 * 1.2 * D
40 m3 = 1.2 * ð * D3/4
D = 3.49 m ~= 3.5 m
H = 4.2 m.
Entonces el estanque posee un volumen de 40 m3, con un diámetro de 3.5 m (Area basal = 9.62 m2) y una altura de 4.2 m, usando un agitador de 15 hp.Bibliografia:
Estanque
R.p.m.
E
8 ton/h Na2CO3
F
Solución NaCl
15%
S
Solución 80% de Na2CO3
Descargar
| Enviado por: | Georgeatos |
| Idioma: | castellano |
| País: | Chile |
