Ingeniero Químico
Velocidad de reacción
Objetivos
Determinar la velocidad de la reacción de descomposición del H2O2 catalizada con una mezcla de MnO2 y Fe2O3. En fracciones fijas de tiempo mediremos el volumen de O2 desprendido según la reacción:
2 H2O2 ! 2 H2O + O2
Introducción
Al estudio de las velocidades a las que tiene lugar las reacciones químicas se denomina cinética química. Este tema es importante en la industria química porque los diseñadores de plantas, de procesos y de equipos, deben conocer como son afectadas las velocidades de reacción por las variaciones de temperatura, presión y concentración.
Entendemos por velocidad de reacción a la variación de la concentración de una sustancia dividido por el tiempo que transcurre para que la variación tenga lugar.
Velocidad = ð[x]/ ðt (1)
Donde:
ð[x] es la variación en la concentración molar de una sustancia x.
ðt es el tiempo en el que tiene lugar la variación.
La unidad de velocidad de reacción es mol / L . s
Una vez se ha formado un producto en una reacción, este puede reaccionar a su vez (incluso con los reactantes originales). Como esta consecuencia, dificulta el análisis de la velocidad de reacción, se suele medir la velocidad inicial de la misma, esto viene a ser la velocidad a la que se inicia la reacción cuando no hay productos presentes.
En la mayoría de los casos, la velocidad inicial depende de las concentraciones iniciales de los reactantes.
A ! B + C (2)
La forma de la ecuación se nos quedará:
Velocidad = k . [A]0 (3)
Donde:
k es una constate.
[A]0 es la concentración inicial del componente A.
Si nos fijamos en esta ecuación, vemos que se corresponde a la ecuación de una línea recta con ordenada en el origen 0 y pendiente k:
Velocidad = 0 + k . [A]0 (4)
Y = a + b . x (5)
No todas las reacciones tienen velocidades iniciales proporcionales a la concentración inicial de un reactante.
2 A (g) ! 2 B (g) + C (g) (6)
en donde su ecuación de velocidad vendrá dada por la expresión:
V = k [A]02 (7)
Donde k es otra constante (no de igual valor que la anterior) que tiene unidades de L/mol.s
Las expresiones que hemos obtenido muestran como dependen las velocidades iniciales de reacción de las concentraciones iniciales de reactante. Con esto, podemos llegar a deducir que, una ecuación de velocidad es una ecuación que expresa la velocidad instantánea de reacción mediante las concentraciones de las sustancias que intervienen en la reacción.
La constante k que aparece en la ecuación de velocidad se denomina constante de velocidad. Es independiente de la concentración de los reactantes pero depende de la reacción y de la temperatura.
Así pues, la velocidad de la reacción se ve afectada, en gran parte, tanto por la concentración de los reactivos como por la temperatura. Más adelante veremos el modelo de colisiones, en donde se explica estos efectos en un nivel molecular.
Las dos ecuaciones de velocidad que hemos visto hasta aquí se diferencian en el exponente al que se eleva la concentración. Ambas pueden resumirse por la ecuación:
V = k . [reactante]a (8)
Con a = 1 para la reacción (3) y a = 2 para la reacción (2)
La reacción (3) diremos que es de primer orden, puesto que la velocidad de reacción es proporcional a la concentración de reactante.
La reacción (7) diremos que es de segundo orden pues, la velocidad de reacción es proporcional al cuadrado de la concentración de la sustancia.
Diremos que una ecuación es de orden cero, si su velocidad es independiente de la concentración. El nombre “orden cero” proviene del hecho matemático de que cualquier cosa elevada a la potencia cero es igual a uno. A estas alturas, podemos afirmar que el orden de una sustancia es la potencia a la que se eleva su concentración en la ecuación de velocidad.
Así pues, llamaremos orden global de una reacción, a la suma de las potencias a las que están elevadas las concentraciones individuales en su ecuación de velocidad.
Por lo tanto, en la siguiente ecuación:
V = k [A]2 [B] (9)
Diremos que la reacción es de segundo orden respecto a A y, de primer orden respecto de B, siendo su orden global 3.
En multitud de ocasiones conocemos la concentración inicial [A]0 de un reactivo pero queremos saber la concentración [a] del mismo un tiempo t más tarde.
Para hallar la [A], necesitaremos una expresión de la concentración en función del tiempo. Tal expresión (obtenida por cálculo matemático) se denomina ecuación integral de velocidad. A continuación daremos las ecuaciones integrales de velocidad para los órdenes de reacción antes mencionados:
Orden cero:
[A]0 / [A] = k . t (10)
Primer orden:
Ln [A]0 / [A] = k . t (11)
Segundo orden:
Ln [A] / [A] 0 = k . t (12)
En nuestra práctica en lugar de utilizar las concentraciones usaremos los volúmenes,
Anteriormente, habíamos comentado que la velocidad de reacción se ve afectada tanto por la concentración de los reactivos como por la temperatura. Una explicación que da cuenta de ambos efectos es el modelo de colisiones de la cinética química. La idea central del modelo es que las moléculas deben chocar para que reaccionen. Cuanto más grande sea el número de colisiones que ocurren por segundo, mayor será la velocidad de reacción. Esta idea nos permite entender el efecto de la concentración sobre la velocidad: conforme aumenta la concentración de las moléculas de reactivo, también lo hace el número de colisiones. De igual forma, podemos comprender el efecto de la temperatura: cuando la temperatura aumenta, también la hace la velocidad de las moléculas, lo cual hace que choquen con más fuerza (con más energía) y, con mayor frecuencia.
En 1888, S. Arrhenius sugirió que las moléculas deben poseer cierta cantidad mínima de energía para reaccionar. De acuerdo con el modelo de colisiones, esta energía proviene de la energía cinética de las moléculas en colisión. Para que dos moléculas reaccionen, deben colisionar con una energía cinética total de magnitud igual o mayor que un cierto valor mínimo. La energía mínima que se requiere para iniciar una reacción se llama energía de activación (Ea), cuyo valor varía de una reacción a otra.
Arrhenius también observó que, para casi todas las reacciones , el aumento de la velocidad con la temperatura no es lineal, sino que obedecen a la ecuación:
k = A . e -Ea/RT (13)
Donde
k es la constante de velocidad.
Ea es la energía de activación.
R es la constante de los gases ideales (8,314 J/mol . K)
T es la temperatura absoluta (K)
A es el factor de frecuencia, este está relacionado con la frecuencia de las colisiones. Suele permanecer constante.
Aunque por comodidad, la utilizaremos en la forma logarítmica:
Ln k = -Ea/RT + ln A
(14)
Ó
Log k = -Ea/2,303 . RT + cte (15)
De esta manera, podemos determiner la energía de activación, si conocemos k a varias temperaturas.
Para finalizar, decir que , otro método para modificar la velocidad de la reacción es el uso de un catalizador. Estos no favorecen o desfavorecen el número de colisiones de las moléculas sino que, se limitan a reducir(o aumentar, dependiendo de lo que deseemos hacer) la energía de activación global de una reacción química, sin sufrir, ninguna alteración permanente.
El catalizador cambia el curso ordinario de la reacción y hace que esta, transcurra por un camino diferente, modificando así, su energía de activación.
El catalizador es incapaz de desplazar el equilibrio de la reacción hacia un lado u otro, pues no altera en absoluto las funciones termodinámicas de la reacción.
Se puede diferenciar tres importantes tipos de catalizadores:
-
Catálisis homogénea, donde el catalizador presente está en la misma fase que las moléculas que reaccionan.
-
Catálisis heterogénea, donde el catalizador existe en una fase diferente a la de las moléculas que reaccionan, comúnmente como un sólido en contacto con reactivos gaseosos o con reactivos en solución líquida.
-
Enzimas, suelen ser proteínas de elevado peso molecular. Catalizan casi todas las reacciones que están ocurriendo constantemente en los seres vivos.
En nuestra práctica utilizaremos catalizadores homogéneos.
Material necesario
Necesitaremos:
- Un soporte con nueces,
- Pinzas,
- Bureta colectora de gases (eudiometro),
- Kitasaltos de boca esmerilada con tapón,
- Un cronómetro,
- Un soporte con nuez y pinza,
- Una bureta de 50 ml
- Un matraz de 1 L.
- Una pipeta de 10 ml
- Un vaso de 50 ml de alto.
También deberemos tener preparada una disolución aproximadamente 0,3 % de H2O2 (sabiendo que es 10 ml de H2O2 al 30%, diluidos en 1 L).Como catalizador se utilizará una mezcla pulverizada de MnO2 y Fe2O3 en proporción 1:2.
El montaje del experimento deberá quedar de la siguiente forma:
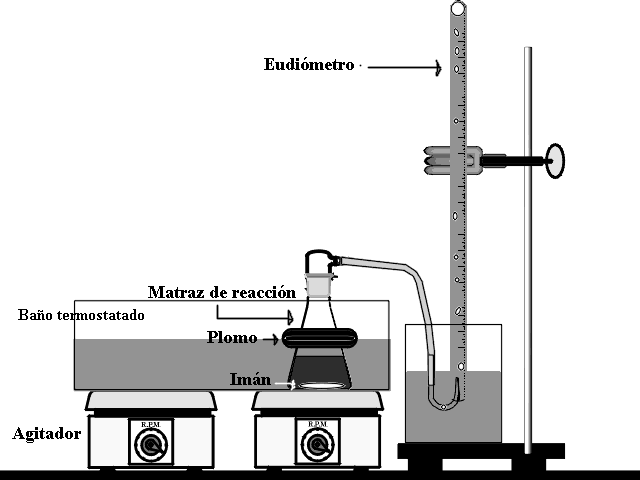
Para ello se llena de agua la bureta y se introduce, invertida, en un baño de agua. La mezcla de reacción se realizará en un kitasaltos, el cual, está introducido en el baño termostático.
Procedimiento experimental:
Como la disolución que tenemos tiene una concentración del 33%, preparamos una concentración del 30% de H2O2.
Si para 30% !1 L
para 33% ! X
30 / 33 " 100 = 9,1 ml
La disolución tendrá 9,1 ml de H2O2 por cada litro de H2O.
Posteriormente pesamos 0,1 g de la mezcla pulverizada de dióxido de manganeso y óxido de hierro (III) en el tubo de ensayo. Seguidamente vertimos 40 ml de la disolución de H2O2 en el kitasaltos y la introducimos en el baño termostático (a una temperatura de 24,5 º C). Tan pronto como pasa la primera burbuja por el eudiómetro activamos el cronometro, midiendo el volumen de gas en intervalos de 30 segundos, durante 300 segundos.
Los resultados obtenidos son los siguientes:
| Medidas tomadas | ||
| Tª 24,5º C | ||
| Muestra | t (s) | Volumen O2 (ml) |
| 1 | 30 | 50 + 0,1 |
| 2 | 60 | 48 + 0,1 |
| 3 | 90 | 46,5 + 0,1 |
| 4 | 120 | 44,8 + 0,1 |
| 5 | 150 | 43,5 + 0,1 |
| 6 | 180 | 40 + 0,1 |
| 7 | 210 | 39,8 + 0,1 |
| 8 | 240 | 37,2 + 0,1 |
| 9 | 270 | 36,1 + 0,1 |
| 10 | 300 | 35,3 + 0,1 |
Puesto que el eudiómetro está invertido, los volúmenes reales obtenidos serán la diferencia entre la medida total del eudiómetro y la medida tomada.
Los datos reales obtenidos serán:
| Medidas corregidas | ||
| Tª 24,5º C | ||
| Muestra | t (s) | Volumen O2 (ml) |
| 1 | 30 | 0 + 0,1 |
| 2 | 60 | 2 + 0,1 |
| 3 | 90 | 3,2 + 0,1 |
| 4 | 120 | 5,2 + 0,1 |
| 5 | 150 | 6,5 + 0,1 |
| 6 | 180 | 10 + 0,1 |
| 7 | 210 | 10,2 + 0,1 |
| 8 | 240 | 12,8 + 0,1 |
| 9 | 270 | 13,9 + 0,1 |
| 10 | 300 | 14,7 + 0,1 |
Ahora obtendremos el orden de la reacción representando sus ecuaciones integradas por mínimos cuadrados, aquella representación que tenga un coeficiente de correlación más próximo a 1 nos indicará el orden:
Si nos fijamos en su coeficiente de correlación, vemos que los datos se ajustan más a una recta de Orden cero, por tanto tenemos que:
y = 0,057.t -1,5533
R2 = 0,9864
k1 = 0,057 L-1s-1
Seguidamente, vamos a repetir todo el proceso pero aumentando la temperatura de la reacción a unos 32,5º C, los datos que obtenemos son los siguientes:
| Medidas tomadas | ||
| Tª 32,5º C | ||
| Muestra | t (s) | Volumen O2 (ml) |
| 1 | 30 | 48.5 + 0,1 |
| 2 | 60 | 46.7 + 0,1 |
| 3 | 90 | 42.2 + 0,1 |
| 4 | 120 | 39.6 + 0,1 |
| 5 | 150 | 36.8 + 0,1 |
| 6 | 180 | 34.8 + 0,1 |
| 7 | 210 | 32.9 + 0,1 |
| 8 | 240 | 30.9 + 0,1 |
| 9 | 270 | 28.9 + 0,1 |
| 10 | 300 | 27.9 + 0,1 |
Obtenemos los volúmenes reales de la misma forma que anteriormente, obtenemos:
| Medidas corregidas | ||
| Tª 32,5º C | ||
| Muestra | t (s) | Volumen O2 (ml) |
| 1 | 30 | 1,5 + 0,1 |
| 2 | 60 | 3,3 + 0,1 |
| 3 | 90 | 7,8 + 0,1 |
| 4 | 120 | 10,4 + 0,1 |
| 5 | 150 | 13,2 + 0,1 |
| 6 | 180 | 15,2 + 0,1 |
| 7 | 210 | 17,1 + 0,1 |
| 8 | 240 | 19,1 + 0,1 |
| 9 | 270 | 21,1 + 0,1 |
| 10 | 300 | 22,1 + 0,1 |
Obtenemos la representación de los ordenes de reacción:
Como en el caso anterior, observamos claramente que la ecuación es de orden cero, por lo tanto, tendremos:
y = 0,0785 . t + 0,1267
R2 = 0,9791
k2 = 0,0785 L-1s-1
Vemos que ambas ecuaciones son de orden cero, para apreciar, claramente, como el efecto de la temperatura modifica la velocidad de la reacción, vamos a representar las dos rectas en una misma gráfica:
En la gráfica apreciamos claramente la influencia de la temperatura en la velocidad de reacción.
La recta se ajusta bastante bien a los datos experimentales, así que podemos despreciar los errores cometidos al tomar las medidas.
Ejercicios post-laboratorio
Deduzcase la ley general que rige el proceso.
En el proceso solo interviene el agua oxigenada, que se separa para dar agua y oxigeno:
2H2O2 ( l ) ! 2H2O( l ) + O2(g)!
Su velocidad de reacción será por tanto:
V = k [H2O2]2
Así pues, se puede decir que, en general, para una reacción, en donde un reactivo se separa para dar dos productos:
aA ! bB + cC
Tendrá una ecuación de velocidad de la forma:
V = k [A]a
¿Por qué se puede usar el volumen de oxígeno desprendido en lugar de su concentración para determinar la velocidad de reacción?
Porque, como hemos dicho anteriormente en la introducción, la concentración o los moles, están directamente relacionados con el volumen:
Partimos de la ecuación de los gases ideales
P Vi = ni R T
Ahora despejamos el número de moles
ni = ( P/ R T) " Vi
Y como la expresión ( P/ R T) es constante, tenemos que el número de moles es directamente proporcional al volumen. Además, nos es más fácil ver como varía el volumen con respecto al tiempo(mediante el montaje descrito antes), que la concentración con respecto al tiempo.
Estimar la energía de activación utilizando la ecuación de Arrhenius, compárese el valor calculado con el de la energía de activación de descomposición del agua oxigenada no catalizada ( 76 kJ/ mol):
Según la ecuación de Arrhenius:
k = A . e -Ea/RT
Cogemos su forma logarítmica y sustituimos las dos constantes de velocidad que hemos obtenido con los datos experimentales:
Ln k1= -Ea/RT + ln A
Ln k2= -Ea/RT + ln A
Ahora le restamos a la segunda ecuación la primera, y nos quedará:
Ln k2/ k1= - Ea / R (1/T1 - 1/ T2)
Sustituyendo los valores y despejando la Ea, tendremos:
Ln 0,0785/0,057 " R /(1/305,65-1/297,65) = -Ea
Ea = 30,8 kJ/ mol
Vemos claramente que la descomposición del agua oxigenada, favorecida por los catalizadores, logra disminuir la energía de activación en un 41 % aproximadamente.
¿Puede existir un catalizador que “frene” la velocidad de reacción?
Sí, son los denominados”catalizadores negativos”o”inhibidores”.
¿Cuál sería en último extremo su efecto?
Retardar mucho tiempo la reacción(semanas, meses, años,…) pero nunca la detendría por completo.
5) La concentración del agua oxigenada se expresa frecuentemente en “Volúmenes”, entendiendo por tales, los litros de oxígeno medidos en condiciones normales que es capaz de producir un litro de solución acuosa de agua oxigenada. Verificar que una solución al 0,3% de H2O2 (0,3 g en 100 mL) corresponde a un volumen.
Tenemos que, en 0,3 g de H2O2 en 100 mL de agua.
Por lo tanto tendremos:
nH2O2 = Peso/ Peso molecular = = 0,3/34,02 =8,818 . 10-3 moles de H2O2
Nuestra reacción es la siguiente:
2H2O2 ( l ) ! 2H2O( l ) + O2(g)!
Por estequiometria, por cada dos mols de H2O2 tenemos uno de O2(g), en 8,818 . 10-3 moles de H2O2 habrán:
n O2 = 8,818 . 10-3/2 = 4,409 . 10-3 mols de O2(g)
En condiciones normales:
n O2 = V O2 / 22,4 L
V O2 = 0,09876 ml por cada 100 ml de disolución
En un litro 0,987 L " 1L (un volumen)
6) ¿Cuáles de las siguientes afirmaciones son ciertas? (justifícalas si lo son, si no, escríbelas correctamente)
Las reacciones endotérmicas son más lentas que las exotérmicas.
Falso…, pues, por regla general(y como hemos visto en esta práctica), al aplicar calor, la reacción sucede más rápidamente, por lo tanto, la correcta afirmación sería:
Por regla genera, las reacciones endotérmicas son más rápidas que las exotérmicas.
El mecanismo de una reacción catalizada es el mismo que sin catalizar.
Verdadero…, pues como ya hemos dicho en la introducción, un catalizador solo se limita a reducir la energía de activación llevando a la reacción “por otro camino”, pero no modifica en absoluto la reacción global.
La velocidad de un proceso es siempre proporcional a la variación de energía libre de dicho proceso.
Verdadero…, pues si el sistema tiene mayor energía interna, sus moléculas vibrarán con mayor energía cinética, favoreciendo los choques entre las moléculas, lo cual hará que la velocidad de la reacción sea mayor, e viceversa, si el sistema tiene menor energía interna, las moléculas vibrarán con menor energía cinética, haciendo que la velocidad de reacción sea menor.
7) Comentar los factores experimentales que afectan la velocidad de reacción.
Ilustrar con ejemplos la influencia de dichos factores.
La temperatura
Pues aumenta la energía cinética de las moléculas y, esto provoca que el número de choques efectivos sea mayor.
Ejemplo: La reacción de descomposición del agua oxigenada a 24,5º C era más lenta que a 32,5º C.
La concentración
Pues, como dijimos en la introducción, contra mayor concentración tengamos de una sustancia, más choques efectivos se producirán.
La naturaleza del reactivo
Dependiendo de que reactivo sea, tendrá una energía de activación u otra, también dependerá si la sustancia tiene enlaces dobles, triples, simples o que clase de reacción queramos llevar a cabo.
Ejemplo:
Fe3+(aq) + Cr2+(aq) ! Fe2+(aq) + Cr3+(aq)
Esta reacción es muy rápida pues consiste en un intercambio de electrones.
CH4(g) + 2 O2(g) ! CO2(g) + 2H2O(l)
Es muy lenta pues requiere la ruptura de seis enlaces y la formación de otros seis.
Catalizadores
Como ya hemos citado en varias ocasiones, modifican la energía de activación.
Ejemplo:
SO2(g) + ½ O2(g) ! SO3(g) Lenta
SO2 + NO2 ! SO3 + NO Rápida
2) NO + ½ O2 ! NO2 Rápida
Vemos que, si catalizamos la reacción inicial, que es lenta, con un óxido de nitrógeno, aunque la reacción transcurra en dos etapas, es más rápida que la inicial.
8) Cuando se calienta ciclopropano a 500ºC se transforma en propeno. Los datos siguientes se obtuvieron experimentalmente:
| t(min) | [Ciclopropano] mM |
| 0 | 1.5 |
| 5 | 1.24 |
| 10 | 1.00 |
| 15 | 0.83 |
Confirmar que la reacción es de primer orden para el C3H6 y calcular la constante de velocidad.
Vamos a representar las tres rectas de las ecuaciones integradas tal y como hemos hecho en la práctica con los datos experimentales:
Lo primero que haremos será pasar las unidades al sistema internacional:
Minutos ! Segundos Milimolar ! Molar
Y obtendremos las siguientes tablas:
| Orden cero | |
| t(s) | [Ciclopropano] M |
| 0 | 0,015 |
| 300 | 0,0124 |
| 600 | 0,01 |
| 900 | 0,0083 |
| Primer orden | |
| t(s) | Ln [Ciclopropano] M |
| 0 | -4,20 |
| 300 | -4,39 |
| 600 | -4,61 |
| 900 | -4,79 |
| Segundo orden | |
| t(s) | Ln 1/[Ciclopropano] M |
| 0 | 4,20 |
| 300 | 4,39 |
| 600 | 4,61 |
| 900 | 4,79 |
Ahora veamos las representaciones:
A la vista de los datos podemos afirmar que la reacción es de primer orden(o de segundo, pues las rectas son idénticas).
La constante de velocidad será la pendiente de la recta:
y = -0,0007x -4,198
k = -7·10-4 M-1s-1
A partir de los datos experimentales que se dan en la siguiente tabla, obtenidos a una temperatura específica, deducir la ley de la reacción teórica:
| Número de experimento | [A] inicial | [B] inicial | Velocidad inicial de formación de AB2 |
| 1 | 1,0 · 10-2 M | 1,0·10-2 M | 1,5· 10-4 M s-1 |
| 2 | 1,0·10-2 M | 2,0·10-2 M | 1,5· 10-4 M s-1 |
| 3 | 2,0·10-2 M | 3,0·10-2 M | 6,0·10-4 M s-1 |
En la tabla podemos observar que, al duplicar la concentración de B, la velocidad de la reacción sigue siendo la misma, manteniendo, claro está, la concentración de A constante.
En cambio, cuando duplicamos la concentración de A, la velocidad se multiplica por cuatro, por tanto, la ley de velocidad será:
V = k [A]2
Se trata de una reacción de segundo orden respecto de A y de orden cero respecto de B, con lo cual, el orden total es dos.
Para obtener k basta con coger una de las experiencias de la tabla y despejar k.
K = 1,5 ·10-4 M s-1/(1,0·10-2)2 M = 1,5 M-1 s-1
La reacción será:
V = 1,5 [A]2
Bibliografías
" Química, J. Morcillo Rubio, M. Fernández González, Ed. Anaya
" Química general, P.W. Atkins, Ed. Omega, S.A., 1992 Barcelona
" Química, La ciencia central, Brown Le May Bursten, Séptima edición, 1998, Ed. Prentice Hall
" Dibujo del montaje experimental extraído de la página:
http://www.uv.es/fqlabo/biologos/Practicas/bcinetica4.htm
Índice
Pág.
Objetivos………………………………………………………. 1
Introducción…………………………………………………….1
Material necesario………………………………………………4
Procedimiento experimental…………………………………….5
Ejercicios post-laboratorio………………………………………11
Bibliografías……………………………………………………..18
Descargar
| Enviado por: | Streapper |
| Idioma: | castellano |
| País: | España |
