Electrónica, Electricidad y Sonido
Teorema de Thévenin y Teorema de Norton
TEOREMA DE THEVENIN
Cualquier circuito, por complejo que sea, visto desde dos terminales concretos, es equivalente a un generador ideal de tensión en serie con una resistencia, tales que:
-
La fuerza electromotriz del generador es igual a la diferencia de potencial que se mide en circuito abierto en dichos terminales
-
La resistencia es la que se "ve" HACIA el circuito desde los terminales en cuestión, cortocircuitando los generadores de tensión y dejando en circuito abierto los de corriente
Para aplicar el teorema de Thévenin, por ejemplo, en el caso de la Figura 6, elegimos los puntos X e Y y, suponemos que desconectamos todo lo que tenemos a la derecha de dichos puntos, (es decir, estamos suponiendo que las resistencias R3 y R4, las hemos desconectado físicamente del circuito original) y miramos atrás, hacia la izquierda.
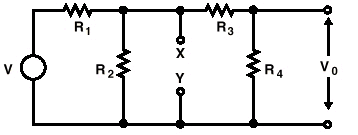
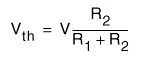
En esta nueva situación calculamos la tensión entre estos dos puntos (X,Y) que llamaremos la tensión equivalente Thévenin Vth que coincide con la tensión en bornes de la resistencia R2 y cuyo valor es :
El siguiente paso es, estando nosotros situados en los puntos indicados (X Y) mirar hacia la izquierda otra vez y calcular la resistencia que vemos, pero teniendo en cuenta que debemos suponer que los generadores de tensión son unos cortocircuitos y los generados de corriente son circuitos abiertos, en el caso de nuestro circuito original, sólo hay un generador de tensión que, para el cálculo que debemos hacer lo supondremos en cortocircuito y ¿ que es lo que vemos ?
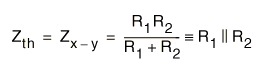
Pues si miráis la figura 6, lo que vemos es que, las resistencias R1 y R2 están en paralelo.
Por lo que la resistencia equivalente Thévenin, también llamada impedancia equivalente, Z th. vale:
El circuito estudiado a la izquierda de los puntos X, Y se reemplaza ahora por el circuito equivalente que hemos calculado y nos queda el circuito de la figura 7, donde ahora es mucho más fácil realizar los cálculos para obtener el valor Vo
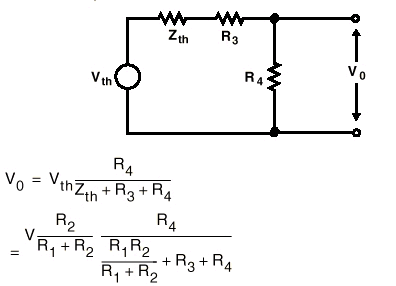
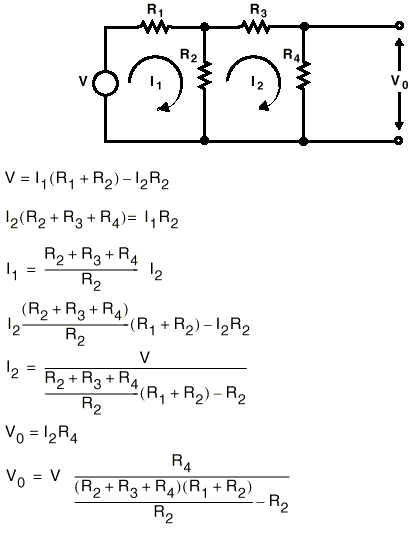
La otra forma de calcular Vo es, la de la teoría de mallas, que calculamos en la figura 8 y donde observamos que los resultados son los mismos. Pero las ecuaciones resultantes son bastante más laboriosas.
En primer lugar se calcula la tensión de salida Vo, proporcionada por el generador V1, suponiendo que el generador V2 es un cortocircuito. A esta tensión así calculada la llamaremos V01 (cuando V2 = 0)
Seguidamente se calcula la tensión de salida Vo, proporcionada por el generador V2, suponiendo que el generador V1 es un cortocircuito. A esta tensión así calculada la llamaremos V02 (cuando V1 = 0)
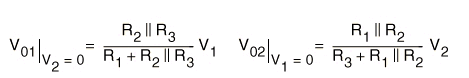
TEOREMA DE NORTON
Cualquier circuito, por complejo que sea, visto desde dos terminales concretos, es equivalente a un generador ideal de corriente en paralelo con una resistencia, tales que:
-
La corriente del generador es la que se mide en el cortocircuito entre los terminales en cuestión.
-
La resistencia es la que se "ve" HACIA el circuito desde dichos terminales, cortocircuitando los generadores de tensión y dejando en circuito abierto los de corriente.-( Coincide con la resistencia equivalente Thévenin)
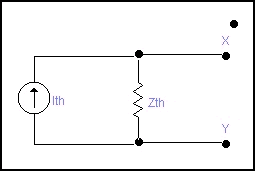
Aplicando el Teorema de Norton al circuito de la figura 6, nos quedará el siguiente circuito:
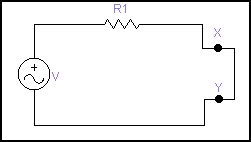
Donde hemos cortocircuitado los puntos X Y de la figura 6. La corriente que circula por entre estos dos puntos la llamaremos Ith y lógicamente es igual a la tensión V del generador de tensión dividido por la resistencia R1 (Ley de OHM) Ith = V / R1 la resistencia Thévenin es la misma que la calculada anteriormente, que era el paralelo de R1 y R2
Zth =R1//R2 = R1 x R2 / (R1 + R2)
5.4 EQUIVALENCIA ENTRE THEVENIN Y NORTON
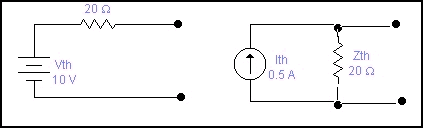
Sea cual sea el equivalente obtenido es muy fácil pasar al otro equivalente sin más que aplicar el teorema correspondiente, así por ejemplo, supongamos que hemos calculado el equivalente Thévenin de un circuito y hemos obtenido el circuito de la izquierda de la figura siguiente :
Aplicando el teorema de Norton a la figura de la izquierda, cortocircuitaremos la salida y calcularemos la corriente que pasa entre ellos que será la corriente : Ith = 10 / 20 = 0,5 A. y la resistencia Norton es 20 W . por lo que nos quedará el circuito equivalente Norton de la derecha
Descargar
| Enviado por: | Tito Edisson |
| Idioma: | castellano |
| País: | España |
