Informática
Sistemas numéricos: decimal y binario
SISTEMAS NUMERICOS
Se definen como reglas o símbolos que nos sirven para mostrar o diagramar cifras o cantidades.
Sistema Binario(base 2)
Sistema Octal(base 8)
Sistema Decimal(base 10)
Sistema Hexadecimal(base 16)
A Manera de Introducción
Antes de entrar de lleno en las bases 2 y 16 que son las bases con las que trabaja el ordenador (en realidad el ordenador sólo trabaja en base 2, la base 16 se utiliza de cara al programador para compactar el número resultante de utilizar la base 2, que sería muy largo y engorroso para utilizar constantemente en los programas)...
... antes de meternos de lleno con éstas bases nos sería muy útil para su entendimiento el saber del porqué de la base decimal.
* Base Decimal (Base 10).
Es la base a la que estamos acostumbrados desde siempre, la base numérica más utilizada.
En esta base 10, contamos con 10 dígitos: 0,1,2,3,4,5,6,7,8 y 9. Mediante estos 10 dígitos podemos expresar cualquier número que deseemos.
El sistema de numeración decimal (base decimal) es un sistema de numeración posicional, al igual que los restantes sistemas que vamos a ver (binario, hexadecimal,etc), y a diferencia del sistema de numeración romano, por ejemplo.
Un sistema posicional es aquel en el que un número viene dado por una cadena de dígitos, estando afectado cada uno de estos dígitos por un factor de escala que depende de la posición que ocupa el dígito dentro de la cadena dada. Es decir, que el dígito 9, valdrá 9 si está al final de la cadena, en la posición reservada para las unidades; valdrá 90 si el dígito se encuentra en la posición reservada para las decenas (2ª posición de derecha a izquierda); valdrá 900 si el dígito se encuentra en la posición reservada para las centenas; etc, etc... A esto es a lo que se le llama posicional, dependiendo de la posición que ocupe un dígito dentro de la cadena numérica, tendrá un valor o tendrá otro. Así por ejemplo, el número 8346 se podría descomponer como sigue: 8346 = (8 * 10^3) + (3 * 10^2) + (4 * 10^1) + (6 * 10^0) .
El factor de escala de que hablábamos arriba, son las diferentes potencias de 10 que multiplican a un dígito dependiendo de su posición dentro de la cadena numérica. Ahora nos podríamos preguntar por qué tenemos como sistema de numeración usual al sistema decimal, por qué es el más usado por todo tipo de gente, a qué se debe que en todo el mundo sea el sistema utilizado por las personas (ya veremos que las máquinas no usan el sistema decimal, sino el binario). Pues es bien sencillo: Porque tenemos 10 dedos. :-) Aún recordaremos eso que nos decían (a quién no?) en clase cuando empezábamos a contar, sumar, etc.. : No vale contar con los dedos!
Intuitivamente, utilizábamos nuestra elemental calculadora: las manos, para contar, realizar sumas y restas sencillas, etc.
Sistema Binario (Base 2)
En esta base sólo contamos con 2 dígitos: 0 y 1. Al igual que la base decimal tiene su razón de ser, la base 2 o binaria tampoco ha surgido debido a un mero convencionalismo, sino que se basa en algo concreto: Electricidad.
Toda la información que se manipula dentro de un ordenador se hace de acuerdo a señales eléctricas. Es lo único que entiende el ordenador. Mediante una señal eléctrica alta, se representa el valor 1; mediante una señal eléctrica baja se representa el 0.
. (1) : Tensión eléctrica alta.
. (0) : Tensión eléctrica baja.
Todo el trabajo del procesador, buses, etc... se realiza de acuerdo a este sistema binario. Cuando se recibe una señal eléctrica alta, se interpreta como que ha llegado un dato de valor (1). Cuando la señal es baja, el dato es un (0). Todo el flujo de datos en el interior del ordenador, y del ordenador con los periféricos, se realiza mediante estas informaciones eléctricas.
Para representar cadenas numéricas, se emplean cadenas de señales eléctricas. Así por ejemplo, para representar el número 10001101 (base 2), el ordenador utilizaría la cadena de señales eléctricas: Tensión alta, Tensión baja, Tensión baja, Tensión baja, Tensión alta, Tensión alta, Tensión baja, Tensión alta. El factor de escala en esta base, son las potencias de 2 que afectan a un dígito dado dependiendo de su posición en la cadena numérica.
Obsérvese que al decir potencias de 2, me estoy refiriendo a potencias de 2 (en base 10). Es decir, para obtener la traducción de ese número en base 2 a su valor correspondiente en base 10, utilizamos las potencias de 2 mencionadas. Estas potencias de 2 en base 10, serían potencias de 10 en base 2. Es decir, el número 10 en base 2 equivale al número 2 en base 10.
Veámoslo más claro.
El número 10100101 se puede traducir a base 10 como:
10100101 = (1*2^7)+(0*2^6)+(1*2^5)+(0*2^4)+(0*2^3)+(1*2^2)+(0*2^1)+(1*2^0).
O lo que es lo mismo: 10100101 (base 2) = 128+0+32+0+0+4+0+1 (base 10) = 165 (base 10)
Base hexadecimal (Base 16).
La base hexadecimal surgió para compactar la información binaria.
Se utiliza un dígito hexadecimal para representar una cadena de 4 dígitos binarios. Teniendo en cuenta que con 4 dígitos binarios podemos representar 16 números diferentes: 0,1,10,11,100,101,110,111,1000,1001,1010, etc... ...Teniendo en cuenta esto, un dígito hexadecimal tiene que poder tomar 16 valores diferentes.
Para la base 10, tenemos 10 dígitos diferentes: del 0 al 9; para la base 2, nos servimos de dos de esos dígitos que ya teníamos para la base 10: el 0 y el 1.
Pero en la base 16, que tenemos 16 dígitos diferentes, no podemos valernos sólo de los dígitos de la base decimal, ya que sólo hay 10 diferentes, y necesitamos 16.
La solución es utilizar letras para representar los 6 dígitos que nos faltan. Tenemos entonces que los dígitos hexadecimales son: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E y F. A equivale a 10 en base 10. B equivale a 11 en base 10. C equivale a 12 en base 10. D equivale a 13 en base 10. E equivale a 14 en base 10. F equivale a 15 en base 10.
Del mismo modo que en la base 10, el último dígito es el 9; en la base 2, el último dígito es el 1; en la base 16, el último dígito será F.
Si sumamos a F una unidad, obtendremos el número 10 (base hexadecimal). Este número 10h (se utiliza el sufijo 'h' para indicar que se trabaja con base hexadecimal, al igual que el sufijo 'b' indica que se está trabajando con base binaria) equivale a 16 en base 10.
El factor de escala en esta base, son las potencias de 16 que afectan a un dígito dado dependiendo de su posición en la cadena numérica. De forma similar que al hablar de la base binaria, al decir potencias de 16, me estoy refiriendo a potencias de 16 (en base 10).
Es decir, para obtener la traducción de ese número en base 16 a su valor en base 10, utilizamos las potencias de 16 mencionadas. Estas potencias de 16 en base 10, serían potencias de 10 en base 16. Es decir, el número 10 en base 16 equivale al número 16 en base 10.
¿Difícil de entender?
Vamos a ver si esto lo aclara:
El número AF34h se puede traducir a base 10 como:
AF34 (base 16) = (10*16^3)+(15*16^2)+(3*16^1)+(4*16^0) (base 10).
O lo que es lo mismo: AF34 = (10*4096)+(15*256)+(3*16)+4 = 40960+3840+48+4 = 44852
Hemos dicho que la base hexadecimal tiene como finalidad compactar la información binaria.
4 dígitos binarios se puden compactar en un sólo dígito hexadecimal. Tomemos por ejemplo el número 1010000101010101b. Nos es más fácil indicar este número mediante su correspondiente número en base hexadecimal. Compactamos entonces toda esa cadena de información binaria en sólo 4 dígitos de información en base hexadecimal. El proceso para llevar a cabo este cambio es sencillo. De derecha a izquierda de la cadena numérica, se van cogiendo cadenas de 4 dígitos binarios, y se transforman a su correspondiente dígito hexadecimal.
Cojamos los primeros 4 dígitos binarios:
0101. 0101 (base 2) = (0*8) + (1*4) + (0*2) + (1*1) = 5 (base 16).
Siguiendo el proceso con el resto de la cadena, tenemos que el número resultante en base 16 es A155h, que es mucho más fácil de recordar y almacenar (en cuanto a código fuente se refiere) que el correspondiente en base 2. En caso de que el número en binario tenga menos de 4 dígitos, se rellenan las posiciones que faltan hacia la izquierda con ceros.
Es decir, si tenemos el número 100101b, al pasarlo a base hexadecimal, tenemos el dígito de las unidades 5 (0101b), y para el dígito de las decenas tenemos que encontrar el correspondiente hexadecimal a la cadena 10b, que es lo mismo que 0010b, O sea 2 en hexadecimal.
Tenemos entonces que 100101b = 25h. Veamos una muestra de números en las tres bases mencionadas para ver sus equivalencias: Decimal Binario Hexadecimal.
| Binario | Octal |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| Binario | Hexadecimal |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Sistema Octal (Base 2)
Al igual que la base hexadecimal, se utiliza para compactar información binaria, pero en este caso, la compactación es menor, de tal manera que casi no se usa. Mientras que en la base hexadecimal con un sólo dígito se puede representar una cadena de 4 dígitos binarios, en la base octal un dígito sólo puede representar 3 dígitos binarios. Los dígitos posibles para la base octal, evidentemente, son los que van del 0 al 7.
A continuación se detalla el procedimiento para obtener el equivalente de un número en cualquiera de las bases expuestas.
Voy a prescindir de dar la teoría del método, para verlo directamente en la práctica.
Tomemos un número dado en cada una de las diferentes bases. Por ejemplo el número 18732 en base decimal, que es 492C en base hexadecimal, y 100100100101100 en base 2.
Veamos cómo se llega de uno de esos números a otro, al cambiar de base.
* Cambio de base 2 a base 10. 100100100101100b = (1*2^14)+(1*2^11)+(1*2^8)+(1*2^5)+(1*2^3)+(1*2^2)= = 16384+2048+256+32+8+4 = 18732 (base 10).
* Cambio de base 10 a base 2.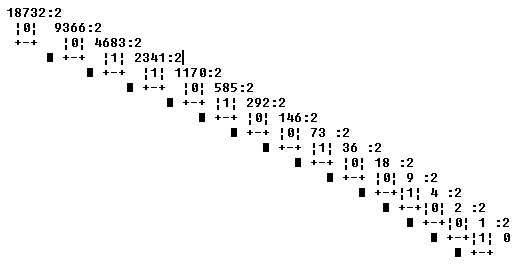
Partiendo del último resto de las sucesivas divisiones, y hasta llegar al primero, obtenemos: 100100100101100b, que es el equivalente en base 2 del número 18732 en base 10.
* Cambio de base 2 a base 16.
100100100101100b = 100 1001 0010 1100 = 492C en base 16. (4) (9) (2) (C)
* Cambio de base 16 a base 2.
492Ch = 0100 1001 0010 1100 = 100100100101100 en base 2.
* Cambio de base 16 a base 10.
492Ch = (4*16^3)+(9*16^2)+(2*16^1)+(12*16^0)= = (4*4096)+(9*256)+(2*16)+(12) = = 16384+2304+32+12 = 18732 en base 10.
* Cambio de base 10 a base 16. 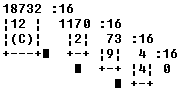
Partiendo del último resto de las sucesivas divisiones, y hasta llegar al primero, obtenemos: 492Ch, que es el equivalente en base 16 del número 18732 en base 10.
Por supuesto, para automatizar el proceso de cambio de bases, existen calculadoras especiales, que permiten trabajar con diferentes bases, permiten representar en cada una de esas bases, realizar operaciones lógicas con los números, etc.
Sistema Octal (Base 2)
Al igual que la base hexadecimal, se utiliza para compactar información binaria, pero en este caso, la compactación es menor, de tal manera que casi no se usa. Mientras que en la base hexadecimal con un sólo dígito se puede representar una cadena de 4 dígitos binarios, en la base octal un dígito sólo puede representar 3 dígitos binarios. Los dígitos posibles para la base octal, evidentemente, son los que van del 0 al 7.
A continuación se detalla el procedimiento para obtener el equivalente de un número en cualquiera de las bases expuestas.
Voy a prescindir de dar la teoría del método, para verlo directamente en la práctica.
Tomemos un número dado en cada una de las diferentes bases. Por ejemplo el número 18732 en base decimal, que es 492C en base hexadecimal, y 100100100101100 en base 2.
Veamos cómo se llega de uno de esos números a otro, al cambiar de base.
* Cambio de base 2 a base 10. 100100100101100b = (1*2^14)+(1*2^11)+(1*2^8)+(1*2^5)+(1*2^3)+(1*2^2)= = 16384+2048+256+32+8+4 = 18732 (base 10).
* Cambio de base 10 a base 2.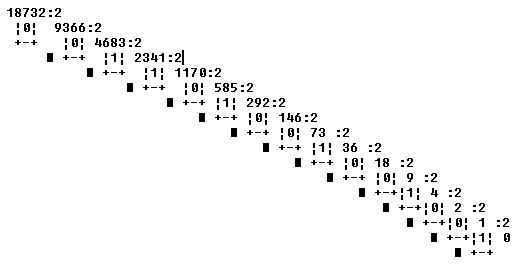
Partiendo del último resto de las sucesivas divisiones, y hasta llegar al primero, obtenemos: 100100100101100b, que es el equivalente en base 2 del número 18732 en base 10.
* Cambio de base 2 a base 16.
100100100101100b = 100 1001 0010 1100 = 492C en base 16. (4) (9) (2) (C)
* Cambio de base 16 a base 2.
492Ch = 0100 1001 0010 1100 = 100100100101100 en base 2.
* Cambio de base 16 a base 10.
492Ch = (4*16^3)+(9*16^2)+(2*16^1)+(12*16^0)= = (4*4096)+(9*256)+(2*16)+(12) = = 16384+2304+32+12 = 18732 en base 10.
-
Cambio de base 10 a base 16.
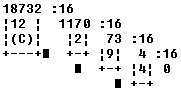
Partiendo del último resto de las sucesivas divisiones, y hasta llegar al primero, obtenemos: 492Ch, que es el equivalente en base 16 del número 18732 en base 10.
Por supuesto, para automatizar el proceso de cambio de bases, existen calculadoras especiales, que permiten trabajar con diferentes bases, permiten representar en cada una de esas bases, realizar operaciones lógicas con los números, etc.
Descargar
| Enviado por: | Hugo Lever |
| Idioma: | castellano |
| País: | Chile |
