Sistemas de representación técnicos y gráficos
Sistemas de representación
Tecnologías de la Información y la Comunicación
Unidad 3
Software: Algoritmos + Datos = Programas
"Es el conjunto de los programas de cómputo, procedimientos, reglas, documentación y datos asociados que forman parte de las operaciones de un sistema de computación."
Extraído del estándar 729 del IEEE
El término «software» fue usado por primera vez en este sentido por John W. Tukey en 1957. En las ciencias de la computación y la ingeniería de software, el software es toda la información procesada por los sistemas informáticos: programas y datos. El concepto de leer diferentes secuencias de instrucciones desde la memoria de un dispositivo para controlar los cálculos fue introducido por Charles Babbage como parte de su máquina diferencial. La teoría que forma la base de la mayor parte del software moderno fue propuesta por vez primera por Alan Turing en su ensayo de 1936, "Los números computables", con una aplicación al problema de decisión.
La palabra «software» se refiere al equipamiento lógico o soporte lógico de un computador digital, comprende el conjunto de los componentes lógicos necesarios para hacer posible la realización de una tarea específica, en contraposición a los componentes físicos del sistema (hardware).
Tales componentes lógicos incluyen, entre otros, aplicaciones informáticas tales como procesador de textos, que permite al usuario realizar todas las tareas concernientes a edición de textos; software de sistema, tal como un sistema operativo, el que, básicamente, permite al resto de los programas funcionar adecuadamente, facilitando la interacción con los componentes físicos y el resto de las aplicaciones, también provee una interface ante el usuario.
Unidad 2
Hardware: dispositivos físicos del ordenador
Los datos: sistemas de representación
Las magnitudes contiguas son las que pueden adoptar los infinitos valores de un intervalo de números reales, tales como la longitud de un segmento, velocidad, temperatura, intensidad de un sonido,etc.
Las magnitudes discretas tienen naturaleza discontinua, tales como la longitud (número de sílabas) de una palbra, capacidad (número de pasajeros) de un vehículo, etc.
En relación con ambos tipos de magnitudes se concidera la información analógica, que es de naturaleza continua, pudiendo tomar infinitos valores; y la información digital, que es de naturaleza discreta y también puede tomar infinitos valores.
En una computadora la información es digital (discreta) y además es finita (podemos almacenar cierta cantidad de información). Las computadoras funcionan mediante señales eléctricas digitales binarias, por lo que la información reprecentada por dichas señales deberá codificarse mediante un sistema de representación digital binario. Así, los distintos símbolos que representan la información humana, letras y números, deberán convertirse a la representación binaria de la computadora.
La razón de ser un computador es el procesamiento de información. Para poder hablar con propiedad de este procesamiento, debemos definir unidades de medida que nos permitan cuantificar de algún modo la acción del computador sobre la información suministrada. Consideramos las siguientes:
-
Bit (Binary Digit) es la cantidad de información que puede almacenarce en una variable bianria. Una variable binaria es la que puede tomar 2 valores estables: 0 ó 1, blaco o negro, si o no, etc.
-
El byte es la cantidad de información que puede codificarse en 8 bits; representa por tanto 2 elevado a la 8 = 256 valores.
Por lo tanto tenemos las siguientes unidades de representación de információn
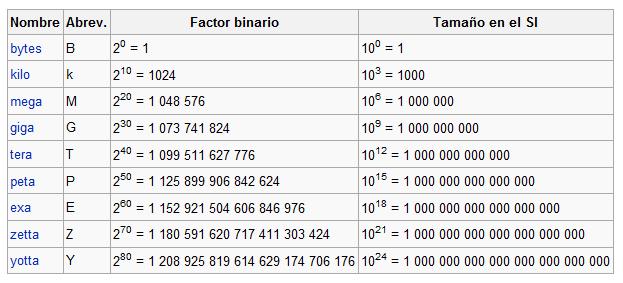
Unidad 2
Hardware: dispositivos físicos del ordenador
Historia de los sistemas de numeración
Introducción. El Concepto de Base
Cuando los hombres empezaron a contar usaron los dedos, guigarros, marcas en bastones, nudos en una cuerda y algunas otras formas para ir pasando de un número al siguiente. A medida que la cantidad crece se hace necesario un sistema de representación más práctico.
En diferentes partes del mundo y en distintas épocas se llegó a la misma solución, cuando se alcanza un determinado número se hace una marca distinta que los representa a todos ellos. Este número es la base. Se sigue añadiendo unidades hasta que se vuelve a alcanzar por segunda vez el número anterior y se añade otra marca de la segunda clase . Cuando se alcanza un número determinado (que puede ser diferente del anterior constituyendo la base auxiliar) de estas unidades de segundo orden, las decenas en caso de base 10, se añade una de tercer orden y así sucesivamente.
La base que más se ha utilizado a lo largo de la Historia es 10 según todas las apariencias por ser ese el número de dedos con los que contamos. Hay alguna excepción notable como son las numeración babilónica que usaba 10 y 60 como bases y la numeración maya que usaba 20 y 5 aunque con alguna irregularidad.
Desde hace 5000 años la gran mayoría de las civilizaciones han contado en unidades, decenas, centenas, millares etc. es decir de la misma forma que seguimos haciéndolo hoy. Sin embargo la forma de escribir los números ha sido muy diversa y muchos pueblos han visto impedido su avance científico por no disponer de un sistema eficaz que permitiese el cálculo.
Casi todos los sistemas utilizados representan con exactitud los números enteros, aunque en algunos pueden confundirse unos números con otros, pero muchos de ellos no son capaces de representar grandes cantidades, y otros requieren tal cantidad de simbolos que los hace poco prácticos.
Pero sobre todo no permiten en general efectuar operaciones tan sencillas como la multiplicación, requiriendo procedimientos muy complicados que sólo estaban al alcance de unos pocos iniciados. De hecho cuando se empezó a utilizar en Europa el sistema de numeración actual, los abaquistas, los profesionales del cálculo se opusieron con las más peregrinas razones, entre ellas la de que siendo el cálculo algo complicado en sí mismo, tendría que ser un metodo diabólico aquel que permitiese efectuar las operaciones de forma tan sencilla.
El sistema actual fue inventado por los indios y transmitido a Europa por los árabes;. Del origen indio del sistema hay pruebas documentales más que suficientes, entre ellas la opinión de Leonardo de Pisa (Fibonacci) que fue uno de los indroductores del nuevo sistema en la Europa de 1200. El gran mérito fue la introducción del concepto y símbolo del cero, lo que permite un sistema en el que sólo diez simbolos puedan representar cualquier número por grande que sea y simplificar la forma de efectuar las operaciones.
Sistemas de Numeracion Aditivos
Para ver cómo es la forma de representación aditiva consideremos el sistema geroglífico egipcio. Por cada unidad se escribe un trazo vertical, por cada decena un símbolo en forma de arco y por cada centena, millar, decena y centena de millar y millón un geroglífico específico. Así para escribir 754 usaban 7 geroglíficos de centenas 5 de decenas y 4 trazos. De alguna forma todas las unidades están fisicamente presentes
Los sistemas aditivos son aquellos que acumulan los simbolos de todas las unidades, decenas... como sean necesarios hasta completar el número. Una de sus características es por tanto que se pueden poner los símbolos en cualquier orden, aunque en general se ha preferido una determinada disposición.
Han sido de este tipo las numeraciones egipcia, sumeria (de base 60), hitita, cretense, azteca (de base 20), romana y las alfabéticas de los griegos, armenios, judios y árabes.
El Sistema de Numeración Egipcio
Desde el tercer milenio A.C. los egipcios usaron un sistema deescribir los números en base diez utilizando los geroglíficos de la figura para representar los distintos ordenes de unidades.
Se usaban tantos de cada uno cómo fuera necesario y se podian escribir indistintamente de izquierda a derecha, al revés o de arriba abajo, cambiando la orientación de las figuras según el caso.
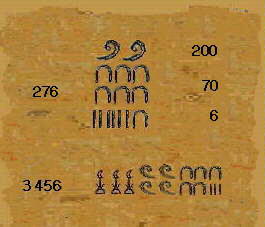
Al ser indiferente el orden se escribían a veces según criterios estéticos, y solían ir acompañados de los geroglíficos correspondientes al tipo de objeto (animales, prisioneros, vasijas etc.) cuyo número indicaban. En la figura aparece el 276 tal y como figura en una estela en Karnak. Estos signos fueron utilizados hasta la incorporación de Egipto al imperio romano. Pero su uso quedó reservado a las inscripciones monumentales, en el uso diario fue sustituido por la escritura hierática y demótica, formas más simples que permitian mayor rapidez y comodidad a los escribas
En estos sistemas de escritura los grupos de signos adquirieron una forma propia, y asi se introdujeron símbolos particulares para 20, 30....90....200, 300.....900, 2000, 3000...... con lo que disminuye el número de signos necesarios para escribir una cifra.
El Sistema de Numeración Griego
El primer sitema de numeración griego se desarrolló hacia el 600 A.C. Era un sistema de base decimal que usaba los símbolos de la figura siguiente para representar esas cantidades. Se utilizaban tantas de ellas como fuera necesario según el principio de las numeraciones aditivas.
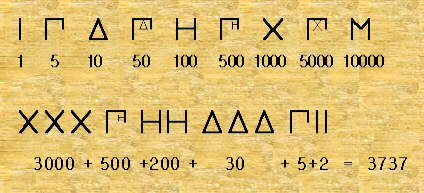
Los símbolos de 50, 500 y 5000 se obtienen añadiendo el signo de 10, 100 y 1000 al de 5, usando un principio multiplicativo. Progresivamente este sistema ático fue reemplazado por el jónico, que empleaba las 24 letras del alfabeto griego junto con algunos otros símbolos según la tabla siguiente
De esta forma los números parecen palabras, ya que están compuestos por letras, y a su vez las palabras tienen un valor numérico, basta sumar las cifras que corresponden a las letras que las componen. Esta circunstancia hizo aparecer una nueva suerte de disciplina mágica que estudiaba la relación entre los números y las palabras. En algunas sociedades como la judía y la árabe, que utilizaban un sistema similar, el estudio de esta relación ha tenido una gran importancia y ha constituido una disciplina aparte: la kábala, que persigue fines místicos y adivinatorios.
Sistemas de Numeracion Híbridos
En estos sistemas se combina el principio aditivo con el multiplicativo. Si para representar 500 los sistemas aditivos recurren a cinco representaciones de 100, los híbridos utilizan la combinación del 5 y el 100. Pero siguen acumulando estas combinaciones de signos para los números más complejos. Por lo tanto sigue siendo innecesario un símbolo para el 0. Para representar el 703 se usa la combinacion del 7 y el 100 seguida del 3.
El orden en la escritura de las cifras es ahora fundamental para evitar confusiones, se dan así los pasos para llegar al sistema posicional, ya que si los signos del 10, 100 etc se repiten siempre en los mismos lugares, pronto alguien piensa en suprimirlos, dándolos por supuestos y se escriben sólo las cifras correspondientes a las decenas, centenas etc. .Pero para ello es necesario un cero, algo que indique que algún orden de magnitud está vacío y no se confundan el 307 con 370, 3070 ...
Además del chino clásico han sido sistemas de este tipo el asirio, arameo, etíope y algunos del subcontinente indio cómo el tamil, el malayalam y el cingalés.
El Sistema de Numeración Chino
La forma clásica de escritura de los números en China se empezó a usar desde el 1500 A.C. aproximadamente. Es un sistema decimal estricto que usa las unidades y los distintas potencias de 10. Utiliza los ideogramas de la figura y usa la combinación de los números hasta el diez con la decena, centena, millar y decena de millar para según el principio multiplicativo representar 50, 700 ó 3000. El orden de escritura se hace fundamental,ya que 5 10 7 igual podría representar 57 que 75.

Tradicionalmente se ha escrito de arriba abajo aunque también se hace de izquierda a derecha como en el ejemplo de la figura. No es necesario un símbolo para el cero siempre y cuando se pongan todos los ideogramas, pero aún así a veces se suprimían los correspondientes a las potencias de 10.
Aparte de esta forma que podríamos llamar canónica se usaron otras. Para los documento importantes se usaba una grafía más complicada con objeto de evitar falsificaciones y errores. En los sellos se escribía de forma más estilizada y lineal y aún se usaban hasta dos grafías diferentes en usos domésticos y comerciales, aparte de las variantes regionales. Los eruditos chinos por su parte desarrollaron un sistema posicional muy parecido al actual que desde que incorporó el cero por influencia india en s. VIII en nada se diferencia de este.
Sistemas de Numeración Posicionales
Mucho más efectivos que los sitemas anteriores son los posicionales. En ellos la posición de una cifra nos dice si son decenas, centenas ... o en general la potencia de la base correspondiente.
Sólo tres culturas además de la india lograron desarrollar un sistema de este tipo. Babilonios, chinos y mayas en distintas épocas llegaron al mismo principio. La ausencia del cero impidió a los chinos un desarrollo completo hasta la intraducción del mismo. Los sistemas babilónico y maya no eran prácticos para operar porque no disponían de simbolos particulares para los dígitos, usando para representarlos una acumulación del signo de la unidad y la decena. El hecho que sus bases fuese 60 y 20 respectivamente no hubiese representado en principio nigún obstáculo. Los mayas por su parte cometían una irregularidad a partir de las unidades de tercer orden, ya que detrás de las veintenas no usaban 20x20=400 sino 20x18=360 para adecuar los números al calendario, una de sus mayores preocupaciones culturales.
Fueron los indios antes del siglo VII los que idearon el sistema tal y como hoy lo conocemos, sin mas que un cambio en la forma en la que escribimos los nueve dígitos y el cero. Aunque con frecuencia nos referimos a nuestro sistema de numeración cómo árabe, las pruebas arqueológicas y documentales demuestran el uso del cero tanto en posiciones intermedias como finales en la India desde el sss. Los árabes transmitieron esta forma de representar los números y sobre todo el cáculo asociado a ellas, aunque tardaron siglos en ser usadas y aceptadas. Una vez más se produjo una gran resistencia a algo por el mero hecho de ser nuevo o ajeno, aunque sus ventajas eran evidentes. Sin esta forma eficaz de numerar y efectuar cálculos dificilmente la ciencia hubiese podido avanzar.
El Sistema de Numeración Babilónico
Entre la muchas civilizaciones que florecieron en la antigua Mesopotamia se desarrollaron distintos sistemas de numeración. En el ssss A.C. se inventó un sistema de base 10, aditivo hasta el 60 y posicional para números superiores.

Para la unidad se usaba la marca vertical que se hacía con el punzón en forma de cuña. Se ponían tantos como fuera preciso hasta llegar a 10, que tenía su propio signo.
De este se usaban los que fuera necesario completando con las unidades hasta llegar a 60.
A partir de ahí se usaba un sistema posicional en el que los grupos de signos iban representando sucesivamente el número de unidades, 60, 60x60, 60x60x60 y asi sucesivamente como en los ejemplos que se acompañan.
El Sistema de Numeración Maya
Los mayas idearon un sistema de base 20 con el 5 cómo base auxiliar. La unidad se representaba por un punto. Dos, tres, y cuatro puntos servían para 2, 3 y 4. El 5 era una raya horizontal, a la que seañadían los puntos necesarios para representar 6, 7, 8 y 9. Para el 10 se usaban dos rayas, y de la misma forma se continúa hasta el 20, con cuatro rayas.
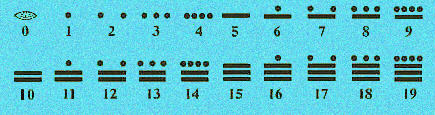
Hasta aquí parece ser un sistema de base 5 aditivo, pero en realidad, considerados cada uno un solo signo, estos símbolos constituyen las cífras de un sistema de base 20, en el que hay que multiplicar el valor de cada cifra por 1, 20, 20x20, 20x20x20 ... según el lugar que ocupe, y sumar el resultado. Es por tanto un sistema posicional que se escribe a arriba abajo, empezando por el orden de magnitud mayor.
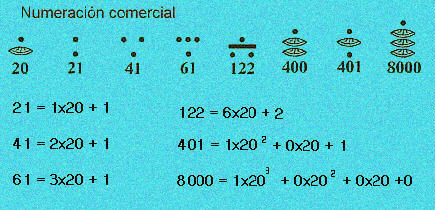
Al tener cada cifra un valor relativo según el lugar que ocupa, la presencia de un signo para el cero, con el que indicar la ausencia de unidades de algún orden, se hace imprescindible y los mayas lo usaron, aunque no parece haberles interesado el concepto de cantidad nula. Cómo los babilonios lo usaron simplemente para indicar la ausencia de otro número.
Pero los científicos mayas eran a la vez sacerdotes ocupados en la observación astronómica y para expresar los número correspondientes a las fechas usaron unas unidades de tercer orden irregulares para la base 20. Así la cifra que ocupaba el tercer lugar desde abajo se multiplicaba por 20x18=360 para completar una cifra muy próxima a la duración de un año.

El año lo consideraban dividido en 18 uinal que constaba cada uno de 20 días. Se añadían algunos festivos (uayeb) y de esta forma se conseguía que durara justo lo que una de las unidades de tercer orden del sistema numérico. Además de éste calendario solar, usaron otro de carater religioso en el que el año se divide en 20 ciclos de 13 días.
Al romperse la unidad del sistema éste se hace poco práctico para el cálculo y aunque los conocimiento astronómicos y de otro tipo fueron notables los mayas no desarrollaron una matemática más allá del calendario.
Actividad 1
Busca ahora tu información sobre el sistema de numeración romana y el sistema de numeración arábiga
Unidad 2
Hardware: dispositivos físicos del ordenador
Historia de los sistemas de numeración
Introducción. El Concepto de Base
Cuando los hombres empezaron a contar usaron los dedos, guigarros, marcas en bastones, nudos en una cuerda y algunas otras formas para ir pasando de un número al siguiente. A medida que la cantidad crece se hace necesario un sistema de representación más práctico.
En diferentes partes del mundo y en distintas épocas se llegó a la misma solución, cuando se alcanza un determinado número se hace una marca distinta que los representa a todos ellos. Este número es la base. Se sigue añadiendo unidades hasta que se vuelve a alcanzar por segunda vez el número anterior y se añade otra marca de la segunda clase . Cuando se alcanza un número determinado (que puede ser diferente del anterior constituyendo la base auxiliar) de estas unidades de segundo orden, las decenas en caso de base 10, se añade una de tercer orden y así sucesivamente.
La base que más se ha utilizado a lo largo de la Historia es 10 según todas las apariencias por ser ese el número de dedos con los que contamos. Hay alguna excepción notable como son las numeración babilónica que usaba 10 y 60 como bases y la numeración maya que usaba 20 y 5 aunque con alguna irregularidad.
Desde hace 5000 años la gran mayoría de las civilizaciones han contado en unidades, decenas, centenas, millares etc. es decir de la misma forma que seguimos haciéndolo hoy. Sin embargo la forma de escribir los números ha sido muy diversa y muchos pueblos han visto impedido su avance científico por no disponer de un sistema eficaz que permitiese el cálculo.
Casi todos los sistemas utilizados representan con exactitud los números enteros, aunque en algunos pueden confundirse unos números con otros, pero muchos de ellos no son capaces de representar grandes cantidades, y otros requieren tal cantidad de simbolos que los hace poco prácticos.
Pero sobre todo no permiten en general efectuar operaciones tan sencillas como la multiplicación, requiriendo procedimientos muy complicados que sólo estaban al alcance de unos pocos iniciados. De hecho cuando se empezó a utilizar en Europa el sistema de numeración actual, los abaquistas, los profesionales del cálculo se opusieron con las más peregrinas razones, entre ellas la de que siendo el cálculo algo complicado en sí mismo, tendría que ser un metodo diabólico aquel que permitiese efectuar las operaciones de forma tan sencilla.
El sistema actual fue inventado por los indios y transmitido a Europa por los árabes;. Del origen indio del sistema hay pruebas documentales más que suficientes, entre ellas la opinión de Leonardo de Pisa (Fibonacci) que fue uno de los indroductores del nuevo sistema en la Europa de 1200. El gran mérito fue la introducción del concepto y símbolo del cero, lo que permite un sistema en el que sólo diez simbolos puedan representar cualquier número por grande que sea y simplificar la forma de efectuar las operaciones.
Sistemas de Numeracion Aditivos
Para ver cómo es la forma de representación aditiva consideremos el sistema geroglífico egipcio. Por cada unidad se escribe un trazo vertical, por cada decena un símbolo en forma de arco y por cada centena, millar, decena y centena de millar y millón un geroglífico específico. Así para escribir 754 usaban 7 geroglíficos de centenas 5 de decenas y 4 trazos. De alguna forma todas las unidades están fisicamente presentes
Los sistemas aditivos son aquellos que acumulan los simbolos de todas las unidades, decenas... como sean necesarios hasta completar el número. Una de sus características es por tanto que se pueden poner los símbolos en cualquier orden, aunque en general se ha preferido una determinada disposición.
Han sido de este tipo las numeraciones egipcia, sumeria (de base 60), hitita, cretense, azteca (de base 20), romana y las alfabéticas de los griegos, armenios, judios y árabes.
El Sistema de Numeración Egipcio
Desde el tercer milenio A.C. los egipcios usaron un sistema deescribir los números en base diez utilizando los geroglíficos de la figura para representar los distintos ordenes de unidades.
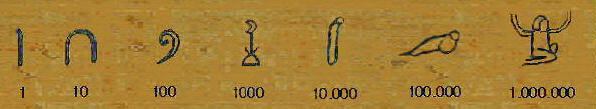
Se usaban tantos de cada uno cómo fuera necesario y se podian escribir indistintamente de izquierda a derecha, al revés o de arriba abajo, cambiando la orientación de las figuras según el caso.
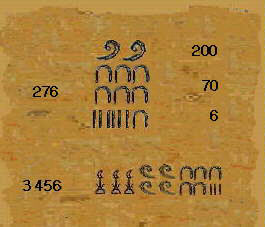
Al ser indiferente el orden se escribían a veces según criterios estéticos, y solían ir acompañados de los geroglíficos correspondientes al tipo de objeto (animales, prisioneros, vasijas etc.) cuyo número indicaban. En la figura aparece el 276 tal y como figura en una estela en Karnak. Estos signos fueron utilizados hasta la incorporación de Egipto al imperio romano. Pero su uso quedó reservado a las inscripciones monumentales, en el uso diario fue sustituido por la escritura hierática y demótica, formas más simples que permitian mayor rapidez y comodidad a los escribas
En estos sistemas de escritura los grupos de signos adquirieron una forma propia, y asi se introdujeron símbolos particulares para 20, 30....90....200, 300.....900, 2000, 3000...... con lo que disminuye el número de signos necesarios para escribir una cifra.
El Sistema de Numeración Griego
El primer sitema de numeración griego se desarrolló hacia el 600 A.C. Era un sistema de base decimal que usaba los símbolos de la figura siguiente para representar esas cantidades. Se utilizaban tantas de ellas como fuera necesario según el principio de las numeraciones aditivas.

Los símbolos de 50, 500 y 5000 se obtienen añadiendo el signo de 10, 100 y 1000 al de 5, usando un principio multiplicativo. Progresivamente este sistema ático fue reemplazado por el jónico, que empleaba las 24 letras del alfabeto griego junto con algunos otros símbolos según la tabla siguiente

De esta forma los números parecen palabras, ya que están compuestos por letras, y a su vez las palabras tienen un valor numérico, basta sumar las cifras que corresponden a las letras que las componen. Esta circunstancia hizo aparecer una nueva suerte de disciplina mágica que estudiaba la relación entre los números y las palabras. En algunas sociedades como la judía y la árabe, que utilizaban un sistema similar, el estudio de esta relación ha tenido una gran importancia y ha constituido una disciplina aparte: la kábala, que persigue fines místicos y adivinatorios.
Sistemas de Numeracion Híbridos
En estos sistemas se combina el principio aditivo con el multiplicativo. Si para representar 500 los sistemas aditivos recurren a cinco representaciones de 100, los híbridos utilizan la combinación del 5 y el 100. Pero siguen acumulando estas combinaciones de signos para los números más complejos. Por lo tanto sigue siendo innecesario un símbolo para el 0. Para representar el 703 se usa la combinacion del 7 y el 100 seguida del 3.
El orden en la escritura de las cifras es ahora fundamental para evitar confusiones, se dan así los pasos para llegar al sistema posicional, ya que si los signos del 10, 100 etc se repiten siempre en los mismos lugares, pronto alguien piensa en suprimirlos, dándolos por supuestos y se escriben sólo las cifras correspondientes a las decenas, centenas etc. .Pero para ello es necesario un cero, algo que indique que algún orden de magnitud está vacío y no se confundan el 307 con 370, 3070 ...
Además del chino clásico han sido sistemas de este tipo el asirio, arameo, etíope y algunos del subcontinente indio cómo el tamil, el malayalam y el cingalés.
El Sistema de Numeración Chino
La forma clásica de escritura de los números en China se empezó a usar desde el 1500 A.C. aproximadamente. Es un sistema decimal estricto que usa las unidades y los distintas potencias de 10. Utiliza los ideogramas de la figura y usa la combinación de los números hasta el diez con la decena, centena, millar y decena de millar para según el principio multiplicativo representar 50, 700 ó 3000. El orden de escritura se hace fundamental,ya que 5 10 7 igual podría representar 57 que 75.
Tradicionalmente se ha escrito de arriba abajo aunque también se hace de izquierda a derecha como en el ejemplo de la figura. No es necesario un símbolo para el cero siempre y cuando se pongan todos los ideogramas, pero aún así a veces se suprimían los correspondientes a las potencias de 10.
Aparte de esta forma que podríamos llamar canónica se usaron otras. Para los documento importantes se usaba una grafía más complicada con objeto de evitar falsificaciones y errores. En los sellos se escribía de forma más estilizada y lineal y aún se usaban hasta dos grafías diferentes en usos domésticos y comerciales, aparte de las variantes regionales. Los eruditos chinos por su parte desarrollaron un sistema posicional muy parecido al actual que desde que incorporó el cero por influencia india en s. VIII en nada se diferencia de este.
Sistemas de Numeración Posicionales
Mucho más efectivos que los sitemas anteriores son los posicionales. En ellos la posición de una cifra nos dice si son decenas, centenas ... o en general la potencia de la base correspondiente.
Sólo tres culturas además de la india lograron desarrollar un sistema de este tipo. Babilonios, chinos y mayas en distintas épocas llegaron al mismo principio. La ausencia del cero impidió a los chinos un desarrollo completo hasta la intraducción del mismo. Los sistemas babilónico y maya no eran prácticos para operar porque no disponían de simbolos particulares para los dígitos, usando para representarlos una acumulación del signo de la unidad y la decena. El hecho que sus bases fuese 60 y 20 respectivamente no hubiese representado en principio nigún obstáculo. Los mayas por su parte cometían una irregularidad a partir de las unidades de tercer orden, ya que detrás de las veintenas no usaban 20x20=400 sino 20x18=360 para adecuar los números al calendario, una de sus mayores preocupaciones culturales.
Fueron los indios antes del siglo VII los que idearon el sistema tal y como hoy lo conocemos, sin mas que un cambio en la forma en la que escribimos los nueve dígitos y el cero. Aunque con frecuencia nos referimos a nuestro sistema de numeración cómo árabe, las pruebas arqueológicas y documentales demuestran el uso del cero tanto en posiciones intermedias como finales en la India desde el sss. Los árabes transmitieron esta forma de representar los números y sobre todo el cáculo asociado a ellas, aunque tardaron siglos en ser usadas y aceptadas. Una vez más se produjo una gran resistencia a algo por el mero hecho de ser nuevo o ajeno, aunque sus ventajas eran evidentes. Sin esta forma eficaz de numerar y efectuar cálculos dificilmente la ciencia hubiese podido avanzar.
El Sistema de Numeración Babilónico
Entre la muchas civilizaciones que florecieron en la antigua Mesopotamia se desarrollaron distintos sistemas de numeración. En el ssss A.C. se inventó un sistema de base 10, aditivo hasta el 60 y posicional para números superiores.

Para la unidad se usaba la marca vertical que se hacía con el punzón en forma de cuña. Se ponían tantos como fuera preciso hasta llegar a 10, que tenía su propio signo.
De este se usaban los que fuera necesario completando con las unidades hasta llegar a 60.
A partir de ahí se usaba un sistema posicional en el que los grupos de signos iban representando sucesivamente el número de unidades, 60, 60x60, 60x60x60 y asi sucesivamente como en los ejemplos que se acompañan.


El Sistema de Numeración Maya
Los mayas idearon un sistema de base 20 con el 5 cómo base auxiliar. La unidad se representaba por un punto. Dos, tres, y cuatro puntos servían para 2, 3 y 4. El 5 era una raya horizontal, a la que seañadían los puntos necesarios para representar 6, 7, 8 y 9. Para el 10 se usaban dos rayas, y de la misma forma se continúa hasta el 20, con cuatro rayas.

Hasta aquí parece ser un sistema de base 5 aditivo, pero en realidad, considerados cada uno un solo signo, estos símbolos constituyen las cífras de un sistema de base 20, en el que hay que multiplicar el valor de cada cifra por 1, 20, 20x20, 20x20x20 ... según el lugar que ocupe, y sumar el resultado. Es por tanto un sistema posicional que se escribe a arriba abajo, empezando por el orden de magnitud mayor.

Al tener cada cifra un valor relativo según el lugar que ocupa, la presencia de un signo para el cero, con el que indicar la ausencia de unidades de algún orden, se hace imprescindible y los mayas lo usaron, aunque no parece haberles interesado el concepto de cantidad nula. Cómo los babilonios lo usaron simplemente para indicar la ausencia de otro número.
Pero los científicos mayas eran a la vez sacerdotes ocupados en la observación astronómica y para expresar los número correspondientes a las fechas usaron unas unidades de tercer orden irregulares para la base 20. Así la cifra que ocupaba el tercer lugar desde abajo se multiplicaba por 20x18=360 para completar una cifra muy próxima a la duración de un año.

El año lo consideraban dividido en 18 uinal que constaba cada uno de 20 días. Se añadían algunos festivos (uayeb) y de esta forma se conseguía que durara justo lo que una de las unidades de tercer orden del sistema numérico. Además de éste calendario solar, usaron otro de carater religioso en el que el año se divide en 20 ciclos de 13 días.
Al romperse la unidad del sistema éste se hace poco práctico para el cálculo y aunque los conocimiento astronómicos y de otro tipo fueron notables los mayas no desarrollaron una matemática más allá del calendario.
Actividad 1
Busca ahora tu información sobre el sistema de numeración romana y el sistema de numeración arábiga
Unidad 2
Hardware: dispositivos físicos del ordenador
Sistema de numeración decimal
El sistema decimal es un sistema de numeración en el que las cantidades se representan utilizando como base el número diez, por lo que se compone de las cifras: cero (0); uno (1); dos (2); tres (3); cuatro (4); cinco (5); seis (6); siete (7); ocho (8) y nueve (9). Este conjunto de símbolos se denomina números árabes. Se trata de un sistema de numeración posicional.
El número de símbolos permitidos en un sistema de numeración posicional se conoce como base del sistema de numeración. Si un sistema de numeración posicional tiene base b significa que disponemos de b símbolos diferentes para escribir los números, y que b unidades forman una unidad de orden superior.
Si contamos desde 0, incrementando una unidad cada vez, al llegar a 9 unidades hemos agotado los símbolos disponibles, y si queremos seguir contando no disponemos de un nuevo símbolo para representar la cantidad que hemos contado. Por tanto añadimos una nueva columna a la izquierda del número, reutilizamos los símbolos de que disponemos, decimos que tenemos una unidad de segundo orden (decena), ponemos a cero las unidades, y seguimos contando.
De igual forma, cuando contamos hasta 99, hemos agotado los símbolos disponibles para las dos columnas; por tanto si contamos (sumamos) una unidad más, debemos poner a cero la columna de la derecha y sumar 1 a la de la izquierda (decenas). Pero la columna de la izquierda ya ha agotado los símbolos disponibles, así que la ponemos a cero, y sumamos 1 a la siguiente columna (centena). Como resultado nos queda que 99+1=100.
Como vemos, un sistema de numeración posicional se comporta como un cuentakilómetros: va sumando 1 a la columna de la derecha y, cuando la rueda de esa columna ha dado una vuelta (se agotan los símbolos), se pone a cero y se añade una unidad a la siguiente columna de la izquierda.
Pero estamos tan habituados a contar usando el sistema decimal que no somos conscientes de este comportamiento, y damos por hecho que 99+1=100, sin pararnos a pensar en el significado que encierra esa expresión.
Tal es la costumbre de calcular en decimal que la inmensa mayoría de la población ni siquiera se imagina que puedan existir otros sistemas de numeración diferentes al de base 10, y tan válidos y útiles como este. Entre esos sistemas se encuentran el de base 2 Sistema binario, de base 8 Sistema octal y el de base 16 Sistema hexadecimal.
Unidad 2
Hardware: dispositivos físicos del ordenador
Teorema Fundamental de la Numeración
Este teorema establece la forma general de construir números en un sistema de numeración posicional. Primero estableceremos unas definiciones básicas:
-
N: Número válido en el Sistema de numeración
-
b: base del sistema de numeración. Número de símbolos permitidos en el sistema.
-
d: un símbolo cualquiera de los permitidos en el sistema de numeración
-
n: número de dígitos de la parte entera.
-
,: coma fraccionaria. Símbolo utilizado para separar la parte entera de un número de su parte fraccionaria.
-
k: número de dígitos de la parte decimal.
La fórmula general para construir un número (cualquier número) N en un sistema de numeración posicional de base b es la siguiente:


El valor total del número será la suma de cada dígito multiplicado por la potencia de la base correspondiente a la posición que ocupa en el número.
Esta representación posibilita la realización de sencillos algoritmos para la ejecución de operaciones aritméticas.
Ejemplo en el Sistema Decimal
En el sistema decimal los símbolos válidos para construir números son {0...9} (0 hasta 9, ambos incluidos), por tanto la base (número de símbolos válidos en el sistema) es 10.
En la figura inferior podemos ver el teorema fundamental de la numeración aplicado al sistema decimal.

Los dígitos a la izquierda de la coma fraccionaria representados por dn ... d2 d1 d0 , toman el valor correspondiente a las potencias positivas de la base (10 en el sistema decimal), en función de la posición que ocupan en el número, y representan respectivamente al dígito de las n-unidades (10n), centenas (10²=100), decenas (10¹=10) y unidades (100=1), ya que como se ve en el gráfico están colocados en las posiciones n..., tercera, segunda y primera a la izquierda de la coma fraccionaria.
Los dígitos a la derecha de la coma fraccionaria d-1, d-2, d-3 ... d-n representan respectivamente al dígito de las décimas (10-1=0,1), centésimas (10-2=0,01), milésimas (10-3=0,001) y n-ésimas (10-n) .
Por ejemplo, el número 1492,36 en decimal, puede expresarse como:

Unidad 2
Hardware: dispositivos físicos del ordenador
Sistema de numeración binaria

El sistema de numeración binario o de base 2 es un sistema posicional que utiliza sólo dos símbolos para representar un número. Los agrupamientos se realizan de 2 en 2: dos unidades de un orden forman la unidad de orden superior siguiente. Este sistema de numeración es sumamente importante ya que es el utilizado por las computadoras para realizar todas sus operaciones.
Conversión de Decimal a Binario
Para la conversión de decimal a binario se emplea el método de las divisiones sucesivas. Se va dividiendo la cantidad decimal por 2, apuntando los residuos, hasta obtener un cociente cero. El último residuo obtenido es el bit más significativo (MSB) y el primero es el bit menos significativo (LSB).
Ejemplo: Convertir el número 15310 a binario.

El resultado en binario de 15310 es 10011001
Conversión de Binario a Decimal
Un número binario se convierte a decimal formando la suma de las potencias de base 2 de los coeficientes cuyo valor sea 1
Ejemplo
Convertir el número 11002 a decimal.
11002 = 1x23 + 1x22 = 1210
Actividad 2
Realiza de esta actividad los ejercicios que tienen que ver con los números binarios aquí
Unidad 2
Hardware: dispositivos físicos del ordenador
ARITMÉTICA BINARIA
Las operaciones de sumar, restar, multiplicar y dividir en el sistema binario se hacen de igual forma que en decimal, sin embargo, es normal que la electrónica interna de las máquinas digitales solo tenga capacidad para sumar. Otras operaciones diferentes a la suma se consiguen mediante un conjunto de sumas: La resta de dos valores se consigue sumando a uno de los valores el complemento del otro, es un truco muy ingenioso que veremos en el siguiente apartado. El producto se hace sumando a sí mismo uno de los factores, tantas veces como indique el otro factor. Su eficacia radica en la gran velocidad de cálculo de los procesadores, siendo frecuente además un coprocesador matemático dedicado solo para operaciones, lo que reduce la carga del procesador central. Por último, una división solo es una cuestión de repartir a partes iguales que se puede conseguir por aproximaciones sucesivas. A título informativo se describen a continuación los 4 tipos de operaciones básicas pero como ya se ha indicado, solo presenta interés la suma.
Ejemplo de suma binaria: En binario, la cifra más alta es el 1, por lo tanto, cuando en la suma encontramos dos unos resulta 1 + 1 = 10, entonces se deja el 0 y se arrastra el 1 para ser sumado a la izquierda. Debido al 1 de arrastre pueden juntarse tres unos, con lo que obtenemos 1 + 1 + 1 = 11 luego dejaremos un 1 y arrastramos otro 1 a la izquierda.
Ejemplo de resta binaria: Se ha puesto un ejemplo de resta en decimal como punto de referencia para restar en binario. Vea que empezando por la derecha, en cuarto lugar encontramos que de 7 a 13 van 6 y arrastramos 1 a la izquierda que se suma al 4 (quedando 5 y faltando 3 para llegar a 8). En sexto lugar encontramos que de 9 a 15 van 6 y arrastramos 1 a la izquierda que se suma al 9. Esto hace que 9 + 1 = 10, con lo que queda 0 (de 0 a 4 van 4) y se arrastra el 1 para sumarse al 1 del extremo izquierdo, con lo que de 2 a 5 van 3. En el ejemplo binario, en cuarto lugar comenzando por la derecha, encontraremos que de 1 a 10 (será 2 pasado a decimal) va 1 y se arrastra 1 a la izquierda para sumar al 0. En sexto lugar volvemos a encontrar que de 1 a 10 va 1 y se arrastra 1 a la izquierda para sumar al 1 (esto desencadena otro arrastre hasta la última posición izquierda).
Ejemplo de producto binario: La multiplicación es tan sencilla que no se necesita explicación. Si sabemos multiplicar en sistema decimal no encontraremos ningún problema para hacerlo en binario. Si el número de cifras es grande, es posible que se junten muchos unos en las sumas finales, por ejemplo 5 unos cuya suma binaria es 101, en cuyo caso queda 1, se arrastra un 0 a la izquierda (que no afecta) y se arrastra un 1 dos lugares a la izquierda. 
Ejemplo de división binaria: En este ejemplo, hay que comenzar cogiendo 4 cifras del dividendo para sobrepasar al divisor. Así resulta que 1011 entre 111 toca a 1 (solo puede ser 1 o 0). 1 por 111 es 111 y falta 100 hasta llegar a 1011. Bajando la siguiente cifra (un 0) resulta que 1000 entre 111 toca a 1. Así sucesivamente. 
Actividad 3
Realiza la Actividad 3 de la web: aquí
Unidad 3
Software: Algoritmos + Datos = Programas
Representación de números enteros - Binario Puro
Los números escritos en Binario Puro (BP) sólo pueden ser positivos, ya que, en este tipo de representación los números negativos no están contemplados. Por tanto, su rango de representación va desde el número 010 hasta el número (2n - 1)10, siendo n el número de bits dedicados a representar a los números enteros. De modo que, en este sistema de numeración, el rango de valores que puede tomar un cierto número x, viene dado por la expresión:

Figura. Rango de representación en Binario Puro.
Ejemplo 1: En Binario Puro, para n = 8, el rango de representación es:

De forma que, se pueden representar 28 = 256 números enteros, que van desde el 010 hasta el 25510.
Ejemplo 2: En Binario Puro, para n = 8, el número 2310se representa de la siguiente manera:

Ejemplo 3: En Binario Puro, para n = 8, los números -6810 y 37910 no se pueden escribir, porque están fuera de su rango de representación (010 <= x <= 25510).
Actividad 4
Si tenemos un odenador de 32 bits significa que n=32, ¿podremos representar el número -5610, el número 3263743610 y el número 34510?
Realiza una tabla indicando para los siguientes valores de n ¿cuál es el valor más pequeño y más grande que podemos representar?
-
n=4
-
n=8
-
n=16
-
n=32
-
n=64
Unidad 3
Software: Algoritmos + Datos = Programas
Representación de números enteros - Magnitud y Signo
En la representación de un número entero en Magnitud y Signo, también llamada Módulo y Signo, de los n bits participantes en dicha representación, el más significativo se encarga de representar al signo del mismo, denominándosele bit de signo. El resto de bits representan a la magnitud. Por tanto, dado un número en Signo Magnitud de n bits
NMS = an-1 an-2 ... a1 a0
el bit an-1 representa al signo del número y el resto de bits: an-2, ..., a1 y a0, a la magnitud del mismo.

De forma que, se pueden representar 28 = 256 números enteros, que van desde el 010 hasta el 25510.
Ejemplo 2: En Binario Puro, para n = 8, el número 2310se representa de la siguiente manera:

Cuando se quiera representar a un número negativo, el bit de signo valdrá 1, siendo 0 cuando el número sea positivo. El rango de representación de este sistema es el siguiente:

Figura. Rango de representación en Signo Magnitud.
Ejemplo 1: En Signo Magnitud, para n = 8, el bit a7 representa al signo del número, y el resto de bits: a6, a5, a4, a3, a2, a1 y a0, a la magnitud del mismo:

Su rango de representación es:

Por consiguiente, se pueden representar 28 - 1 = 255 números enteros, que van desde el -12710 hasta el 12710.
Ejemplo 2: En Signo Magnitud, para n = 8, el número 2310 se escribe:

Al ser un número positivo, el bit de signo vale cero (a7 = 0) y, como se puede observar, los números positivos escritos en Magnitud y Signo se representan igual que si se escribiesen en Binario Puro:
2310 = 00010111MS = 00010111BP
Ejemplo 3: En Magnitud y Signo, para n = 8, el número -2310 se simboliza con la misma magnitud que el número 2310, diferenciándose, solamente, en el bit de signo, que al tratarse de un número negativo, ahora tiene que valer 1, en vez de 0. Así pues, su representación es:

Por tanto, -2310 = 10010111MS
Por otro lado, para calcular el valor en base 10 de un número entero (N) escrito en Signo Magnitud, hay que hacer uso de la fórmula:

Figura. Fórmula para calcular, en base 10, el valor de un número entero escrito en Signo Magnitud.
Ejemplo 4: Para calcular los valores en base 10 de los números 11100001MS y 00011010MS, se debe emplear la fórmula anterior. De tal manera que:
11100001MS = ( (1 - 2∙1) ∙ (1∙26 + 1∙25 + 1∙20) )10 =
= ( (1 - 2) ∙ (64 + 32 + 1) )10 = ( (-1) ∙ (97) )10 = -9710
00011010MS = ( (1 - 2∙0) ∙ (1∙24 + 1∙23 + 1∙21) )10 =
= ( (1 - 0) ∙ (16 + 8 + 2) )10 = ( (1) ∙ (26) )10 = 2610
Obsérvese que, en Signo Magnitud, al problema de desbordamiento se le suma que el número 010 tiene dos representaciones.
Ejemplo 5: En Signo Magnitud, para n = 8, el número 010 se puede escribir de dos formas: 010 = 00000000MS = 10000000MS
Actividad 5
Representa los siguientes números en Modulo y Signo utlizando 8 bits (n = 8)
-
43
-
81
-
-16
-
-74
-
-121
Unidad 3
Software: Algoritmos + Datos = Programas
Representación de números enteros - Complemento a 1, complemento a 2 y Exceso a 2n-1
Actividad 6
Si recordamos que el motivo por el que utilizamos un sistema de numeración posicional es para poder realizar la operaciones matemáticas básicas (suma, resta y multiplicación) de manera sencilla vamos a pensar en la manera en la que se realizan dichas operaciones en binario.
Primero veremos que modulo y signo no es la mejor manera de representar los números en binario cuando tenemos números negativos y deseamos operar con ellos.
Primera parte
Intenta realizar las siguientes operaciones en Modulo y Signo directamente en binario e indica las dificultades que has tenido (para ello comprueba que el resultado es correcto)
a) 01100101 + 00001100
b) 00010010 + 10000111
c) 01000101 - 00111111
d) 00010111 - 01100000
Segunda parte
Busca en Internet como se representan los números utilizando los métodos de complemento a 1, complemento a 2 y exceso a 2n-1, explícalo y pon algun ejemplo
A continuación rellena la siguiente tabla
| Decimal | Binario Puro | Módulo y Signo | Complemento a 1 | Complemento a 2 | Exceso a 2n-1 |
| 13 | 00001101 | 00001101 | 00001101 | 00001101 | 10001101 |
| -3 | No se puede | 10000011 | 11111100 | 11111101 | 01111101 |
| 45 |
|
|
|
|
|
| 142 |
|
|
|
|
|
| -71 |
|
|
|
|
|
| -135 |
|
|
|
|
|
|
|
|
|
| 11101010 |
|
|
|
|
|
|
| 01101010 |
Tercera parte
Indica de las siguientes operaciones cuales se pueden hacer con cada método
| Operación | Binario Puro | Módulo y Signo | Complemento a 1 | Complemento a 2 | Exceso a 2n-1 |
| Sumar dos positivos | Se puede | Se puede | Se puede | Se puede | Se puede |
| Restar dos positivos con resultado negativo | No se puede |
|
|
|
|
| Sumar uno positivo y otro negativo con resultado positivo |
|
|
|
|
|
| Sumar uno positivo y otro negativo con resultado negativo |
|
|
|
|
|
| Sumar dos negativos |
|
|
|
|
|
| Multiplicar dos negativos |
|
|
|
|
|
| Multiplicar uno positivo y otro negativo |
|
|
|
|
|
Unidad 3
Software: Algoritmos + Datos = Programas
Representación de números enteros - BCD
El BCD (Binary Coded Decimal) sirve para codificar en binario los dígitos del Sistema Decimal. Para ello, se utiliza la tabla de correspondencias de la tabla siguiente, en donde se puede ver que a cada dígito decimal se le hace corresponder su codificación en Binario Puro con cuatro bits.

Figura. Tabla de correspondencias entre los dígitos de los Sistemas Decimal y BDC.
Ejemplo: Si se quiere pasar el número 670910 a BCD, utilizando la tabla de correspondencias entre los dígitos de los Sistemas Decimal y BCD, se obtiene que:

Por tanto, 670910 = 0110011100001001BCD
Actividad 7
Realiza las siguientes conversiones:
Converte de base 10 a BDC
-
2134
-
923
-
Converte de BCD a base 10
-
011000001001
-
0001001000110100
-
Gráficos: Es la representación gráfica de las operaciones que realiza un algoritmo (diagrama de flujo).
-
No Gráficos: Representa en forma descriptiva las operaciones que debe realizar un algoritmo (pseudocodigo).
-
INICIO
-
Edad: Entero
-
ESCRIBA “cual es tu edad?”
-
Lea Edad
-
SI Edad >=18 entonces
-
ESCRIBA “Eres mayor de Edad”
-
FINSI
-
ESCRIBA “fin del algoritmo”
-
FIN
-
Algoritmo para ir a la escuela
-
Suena el despertador.
-
Se levanta de la cama.
-
Se baña.
-
Se viste.
-
Se desayuna.
-
Toma su mochila.
-
Se va a la escuela.
-
Preguntar sí se va en coche a en autobús.
-
Si se va en coche seguir con la 10.
-
Si es en autobus: esperar el autobus y tomarlo.
-
Llegar a la escuela.
-
Juega a este juego y encuentra el orden correcto para resolver el puzzle
-
el sistema operativo: es el núcleo de cualquier sistema de computación; supervisa y controla todas las actividades de I/O (input-ouput, entrada-salida) y procesamiento de un sistema de computación. Todo el hardware y el software se controla por medio del sistema operativo.
-
la interfaz gráfica para usuario (GUI, Grafical user interface): Cuando se usa software con base en texto y controlado por comandos (v.g.: MS-DOS) se debe ser explícito; si se omite información necesaria en un comando o el formato del comando es incorrecto, aparece un mensaje de error y/o un indicador en pantalla que solicitará que se vuelva a escribir el comando. Una interfaz es una capa opcional de software amigable entre el usuario y una interfaz controlada por comandos Las GUI depende de software con base en gráficos y permite la integración de texto con imágenes gráficas de alta resolución. Los usuarios de la GUI interactúan con el sistema operativo y otro software usando un dispositivo de indicación y un teclado para dar comandos. El usuario selecciona de las opciones que se presentan en la pantalla, ya sea en los menúes o por medio de un ícono (representación gráfica que simboliza una actividad de procesamiento). Las GUI han eliminado la necesidad de memorizar y escribir comandos complicados.
-
Historia de los distintos sistemas operativos
-
Sistemas operativos actuales
-
Editores de texto
-
Compiladores
-
Intérpretes
-
Enlazadores
-
Depuradores
-
Entornos de Desarrollo Integrados (IDE): Agrupan las anteriores herramientas, usualmente en un entorno visual, de forma que el programador no necesite introducir múltiples comandos para compilar, interpretar, depurar, etc.. Habitualmente cuentan con una avanzada interfaz gráfica de usuario (GUI).
-
Busca para que sirven cada unos de los programas que se pueden incluir como software de programación y dos ejemplos de cada uno de ellos.
-
Busca la definición de lenguaje de programación y algunos ejemplos de lenguaje de programación.
-
Aplicaciones de Sistema de control y automatización industrial
-
Aplicaciones ofimáticas
-
Software educativo
-
Software médico
-
Software de Cálculo Numérico
-
Software de Diseño Asistido (CAD)
Unidad 3
Software: Algoritmos + Datos = Programas
Representación de números reales - Estándar IEEE 754
Para representar los números reales disponemos de varios métodos de representación, pero el más común es el estándar IEEE 754.
Actividad 8 - Opcional
Busca en Internet cómo funciona este método de representación y explícalo con algunos ejemplos
Unidad 3
Software: Algoritmos + Datos = Programas
Representación de caracteres - EBCDIC
El EBCDIC (Extended Binary Coded Decimal Interchange Code) fue inventado por IBM (International Business Machines Corporation) y utiliza grupos de 8 bits para codificar caracteres en binario, permitiendo representar a 28 = 256 caracteres. Actualmente casi no se utiliza, pero se pueden encontrar en Internet las tablas de carácteres.
Unidad 3
Software: Algoritmos + Datos = Programas
Representación de caracteres - ASCII
El Código Estándar Americano para el Intercambio de Información (American Standard Code for Information Interchange, ASCII) es, hoy en día, el código más utilizado en los equipos informáticos. ASCII emplea grupos de 7 bits para codificar caracteres en binario, permitiendo representar a 27 = 128 caracteres. Su tabla de correspondencias es la siguiente:

Figura. Tabla de correspondencias entre los dígitos de los Sistemas Decimal y BDC.
Los dígitos que rodean la tabla sirven para identificar al número decimal que corresponde a cada carácter. De modo que, para un determinado carácter, el número decimal que le corresponde se obtiene de agrupar los dígitos de su fila y de su columna.
Por ejemplo, al carácter H del ASCII le corresponde la agrupación de los dígitos (7) de su fila y (2) de su columna, es decir, el carácter H se codifica con el código 7210 = 10010002.
Unidad 3
Software: Algoritmos + Datos = Programas
Representación de caracteres - EBCDIC
Unicode es un código que intenta contener a todos los símbolos que se utilizan en todos los idiomas utilizados por los seres humanos (árabe, castellano, chino, coreano, inglés, japonés, etc.). Para ello, utiliza grupos de 16 bits, permitiendo representar a 216 = 65536 caracteres.
Unidad 3
Software: Algoritmos + Datos = Programas
Introducción: Programas
La computadora no solamente es una maquina que puede realizar procesos para darnos resultados, sin que tengamos la noción exacta de las operaciones que realiza para llegar a esos resultados. Con la computadora además de lo anterior también podemos diseñar soluciones a la medida, de problemas específicos que se nos presenten. Mas aun, si estos involucran operaciones matemáticas complejas y/o repetitivas, o requieren del manejo de un volumen muy grande de datos.
El diseño de soluciones a la medida de nuestros problemas, requiere como en otras disciplinas una metodología que nos enseñe de manera gradual, la forma de llegar a estas soluciones.
A las soluciones creadas por computadora se les conoce como programas y no son mas que una serie de operaciones que realiza la computadora para llegar a un resultado, con un grupo de datos específicos. Lo anterior nos lleva al razonamiento de que un programa nos sirve para solucionar un problema especifico.
Para poder realizar programas, además de conocer la metodología mencionada, también debemos de conocer, de manera especifica las funciones que puede realizar la computadora y las formas en que se pueden manejar los elementos que hay en la misma.
Unidad 3
Software: Algoritmos + Datos = Programas
Algortimos
La palabra algoritmo se deriva de la traducción al latín de la palabra árabe alkhowarizmi, nombre de un matemático y astrónomo árabe que escribió un tratado sobre manipulación de números y ecuaciones en el siglo IX.
Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir, para dar solución a un problema específico.
Lenguajes Algorítmicos
Un Lenguaje algorítmico es una serie de símbolos y reglas que se utilizan para describir de manera explícita un algoritmo.
Tipos de Lenguajes Algorítmicos

Actividad
Unidad 3
Software: Algoritmos + Datos = Programas
Software de Sistema
El Software de sistema, en algunas ocasiones también denominado software de base, consiste en un software que sirve para controlar e interactuar con el sistema, proporcionando control sobre el hardware y dando soporte a otros programas.
Este Software coordina las operaciones de hardware y lleva a cabo las tareas ocultas que el usuario rara vez observa. Controla o respalda a los otros tipos de software. Dentro de este tipo de software se encuentran:
Actividad 9
Realiza un trabajo sobre los sistemas operativos en el que aparezcan estos dos aspectos:
Unidad 3
Software: Algoritmos + Datos = Programas
Software de programación
Software de programación: Es el conjunto de herramientas que permiten al programador desarrollar programas informáticos, usando diferentes alternativas y lenguajes de programación, de una manera práctica. Incluye entre otros:
Actividad 10
Actividad Opcional
Realizar un mural con la historia de los lenguajes de programación (Se puede realizar en grupo, máximo tres personas)
Unidad 3
Software: Algoritmos + Datos = Programas
Software de aplicación
El Software de aplicación es aquel que permite a los usuarios llevar a cabo una o varias tareas específicas, en cualquier campo de actividad susceptible de ser automatizado o asistido, con especial énfasis en los negocios. Incluye entre otros:
Descargar
| Enviado por: | Rsl |
| Idioma: | castellano |
| País: | España |
