Industria y Materiales
Series Cronológicas
UNIVERSIDAD GRAN MARISCAL DE AYACUCHO
ESCUELA DE INGENIERIA DE MANTENIMIENTO MENCION INDUSTRIAL

SERIES CRONOLÓGICAS
CIUDAD BOLIVAR, 06 DE DICIEMBRE DE 2007
INDICE
PÁG
INTRODUCCION 3
MARCO TEORICO:
Series Cronológicas. Concepto 4
Representación de una Serie Temporal 4
Componentes de una Serie Temporal 4
Análisis de la Tendencia 7
Ejemplo de una Serie Cronológica 12
Método Gráfico 12
Método de las medias móviles 13
CONCLUSION 14
INTRODUCCION
Una serie cronológica requiere de la elección de un modelo (multiplicativo o aditivo) y la determinación de los cuatro movimientos característicos descritos anteriormente, para lo cual se requiere de un procedimiento que facilite y estandarice las operaciones, todo lo cual es independiente de la naturaleza de la magnitud objeto de estudio.
El análisis de una serie cronológica consta de los siguientes aspectos: recolección de datos fiables, representación gráfica de los datos de la serie y valoración cualitativa de su comportamiento; determinación de la tendencia, determinación de la existencia o no de estacionalidad. En caso afirmativo, obtener el índice correspondiente y proceder a suprimir este movimiento en los datos. ajuste de los datos desestacionalizados a la tendencia, si procede, Registro de las variaciones cíclicas si aparecen, señalando la periodicidad y amplitud de la oscilación alrededor de la tendencia, determinación de los movimientos irregulares, evaluar los resultados obtenidos, en particular las fuentes de error y su magnitud, así como si el proceso se encuentra bajo control estadístico o no.
MARCO TEORICO
SERIES CRONOLOGICAS
Concepto.-
Una serie cronológica o temporal es un conjunto de observaciones de una variable, ordenadas según transcurre el tiempo.
En una serie de tiempo las observaciones no se deben ordenar de mayor a menor debido a que se perdería el grueso de la información debido a que nos interesa detectar como se mueve la variable en el tiempo es muy importante respetar la secuencia temporal de las observaciones.
Representación de una Serie Temporal
Para realizar la representación de una serie temporal se debe realizar mediante una gráfica de dispersión x-y como se muestra en la fig.1
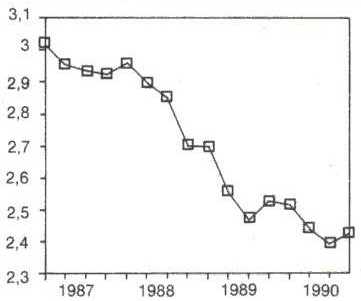
Fig.1. Representación de una serie temporal
Componentes de una serie temporal
1) Tendencia
La tendencia es un movimiento de larga duración que muestra la evolución general de la serie en el tiempo.
La tendencia es un movimiento que puede ser estacionario o ascendente, y su recorrido, una línea recta o una curva. Algunas de la posibles formas son las que se muestran en la fig.2
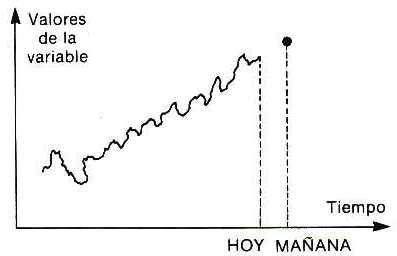
Fig.2. Representación de la tendencia
La tendencia es un movimiento que puede ser estacionario o ascendente o descendente como se indica en la fig.3
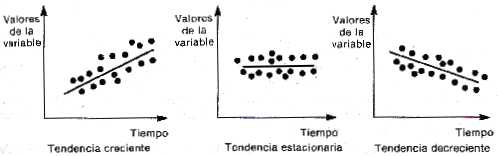
Fig. 3 Tendencias ascendente, estacionaria y descendente
También son posibles algunas formas para la tendencia, que no necesariamente tiene una distribución de puntos en forma aproximadamente lineal sino como las que se muestran en la fig. 4
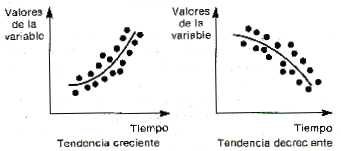
Fig.4 Líneas de tendencia de otras posibles formas.
2) Variaciones estacionales.
Se habla de este tipo de variaciones usualmente cuando el comportamiento de la variable en el tiempo en un periodo esta relacionado con la época o un periodo particular, por lo general en el espacio cronológico presente.
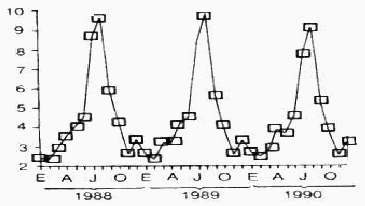
Fig. 5 Variaciones estacionales
3) Variaciones cíclicas
Se llama así a las oscilaciones a lo largo de una tendencia con un período superior al año. El ciclo sugiere la idea de que este tipo de movimiento se repite cada cierto periodo con características parecidas. Los ejemplos mas frecuentes se encuentran en el campo de las variables económicas, en estos casos se deben principalmente a la alternancia de las etapas de prosperidad y depresión en la actividad económica.
4) Variaciones residuales
Cuando aparecen hechos imprevistos, repentinos que afecten las variables en estudio acotando que no podemos preveer nos hallamos frente a variaciones residuales provocadas por factores externos aleatorios.
Por ejemplo un día lluvioso y frío durante el verano es díficil de predecir y aunque perturbaría ciertas actividades diarias como la venta de helados no afectaría en este caso significativamente la serie.
Análisis de la Tendencia
En la práctica es difícil distinguir la tendencia del comportamiento cíclico. Por ejemplo la gráfica puede conducirnos a concluir que existe una tendencia ascendente en la parte de 1980 a 1982, pero esto es una parte de la serie de tiempo más grande.
![]()
Fig, 6 Tendencias entre periodos de tiempo
El análisis de una serie cronológica requiere de la elección de un modelo (multiplicativo o aditivo) y la determinación de los cuatro movimientos característicos descritos anteriormente, para lo cual se requiere de un procedimiento que facilite y estandarice las operaciones, todo lo cual es independiente de la naturaleza de la magnitud objeto de estudio.
Metodológicamente, el análisis de una serie cronológica consta de los siguientes aspectos:
- Recolección de datos fiables.
- Representación gráfica de los datos de la serie y valoración cualitativa de su comportamiento.
- Determinación de la tendencia.
- Determinación de la existencia o no de estacionalidad. En caso afirmativo, obtener el índice correspondiente y proceder a suprimir este movimiento en los datos.
- Ajuste de los datos desestacionalizados a la tendencia, si procede.
- Registro de las variaciones cíclicas si aparecen, señalando la periodicidad y amplitud de la oscilación alrededor de la tendencia.
- Determinación de los movimientos irregulares.
- Evaluar los resultados obtenidos, en particular las fuentes de error y su magnitud , como si el proceso se encuentra bajo control estadístico o no.
Es importante señalar que al determinar cada uno de los movimientos (tendencia, estacionalidad, periodicidad y aleatorios) se debe realizar una discusión de la correspondencia de los resultados obtenidos con lo esperado en dependencia de la naturaleza de los datos, con vistas a brindar una valoración cualitativa del comportamiento de la magnitud bajo estudio y con ello facilitar la adopción de las acciones más adecuadas.
Igualmente debe significarse que en todos los análisis realizados, no se ha efectuado referencia alguna a la naturaleza de los datos que componen la serie, por lo cual los fundamentos teóricos expresados son aplicables a la evaluación de magnitudes tan diversas como pueden ser niveles de lluvia, demanda de combustible, niveles de precios, importe de los cobros y pagos, etc.
Recolección de datos fiables
En las respuestas numéricas a problemas el aspecto de mayor importancia radica en que los datos generalmente contienen errores que deben ser considerados al interpretar los resultados obtenidos y que se originan en las cuatro áreas fundamentales siguientes:
- Errores por parte del operador durante el proceso de incorporación de los datos al sistema. Este tipo de error no puede ser ignorado. Si existen errores en los datos, las soluciones o resultados que proporciona el sistema serán inútiles en su totalidad o de manera parcial, en dependencia de la magnitud del error. Esta posibilidad hace que los resultados obtenidos deban ser analizados críticamente y no confiar ciegamente en los mismos. La revisión de los datos utilizados en los cálculos es una forma de minimizar la presencia de este tipo de error.
- Los inherentes a la formulación del problema. El procedimiento para reducir este tipo de error es mejorar el modelo utilizado en la formulación del problema hasta que el error a que conduce esté en correspondencia con la precisión y exactitud de los datos disponibles. Generalmente la precisión del modelo está estrechamente relacionada con el conocimiento existente del problema cuya solución se acomete. Es importante señalar que este tipo de error condiciona la validez de los resultados sin importar cuan exactos sean los cálculos numéricos realizados por el sistema de cómputo.
- Las relacionadas con la incertidumbre en la determinación de los datos. Este problema es causado por el error en los instrumentos de medición utilizados, que en el caso de la Contabilidad se encuentra asociado al registro correcto de las operaciones.
- Aquellos en que se incurre durante la determinación numérica de la solución. Este tipo de error es causado por la representación necesariamente aproximada en la computadora, mediante un número finito de dígitos, de los números reales, tales como el resultado de la división de 2 entre 3, los números e y ၰ, etc. Esta característica conduce a la existencia de dos tipos de errores: por truncamiento, que proviene del cálculo numérico de una expresión cuando se desprecian a partir de un término los restantes dígitos y errores por redondeo, debido a que los cálculos aritméticos casi nunca pueden llevarse a cabo con una completa exactitud, ya que muchos números tienen una representación decimal infinita y deben ser expresados de forma finita.
Determinación de la tendencia (T)
Un método estadístico ampliamente utilizado para la determinación de la tendencia de un conjunto de datos es el ajuste por mínimos cuadrados de una función. En el caso de la dependencia lineal, la ecuación de la tendencia es Ti = a + b * ti, donde:
ti : Intervalo de tiempo.
Ti: Valor estimado de la magnitud objeto de estudio en el período i.
a : Término independiente, que se obtiene a través de la expresión ![]()
.
b : Pendiente que puede obtenerse mediante la ecuación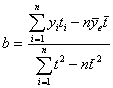
.
![]()
: valor promedio de la magnitud bajo estudio.
![]()
: valor promedio del periodo analizado de la magnitud bajo estudio
n : cantidad de periodos de que consta la serie de datos de la magnitud bajo estudio.
yi : representa el valor real de la magnitud bajo estudio en el periodo i.
Los restantes símbolos utilizados en la determinación de a y b representan los respectivos valores medios de la magnitud bajo estudio y el tiempo, que están dados por las ecuaciones:
![]()
![]()
Determinación de la existencia de estacionalidad (S)
Para la determinación de la existencia o no de estacionalidad en los datos puede utilizarse el Método del Porcentaje Promedio, que consta de los pasos siguientes:
- Paso I: Calcular el promedio mensual de cada año.
- Paso II: Dividir el valor de la serie de cada mes entre el promedio mensual de todos los años considerados de ese propio mes.
- Paso III: Sumar el porcentaje de cada mes obtenido en el paso anterior y dividirlo entre el número de años incluidos en la serie.
- Paso IV: Sumar la media mensual obtenida en el Paso III.
- Paso V: Calcular el índice de estacionalidad dividiendo la suma obtenida en el Paso IV entre 1200.
- Paso VI: Proceder a desestacionalizar los datos dividiendo los valores registrados en cada mes por el índice mensual correspondiente obtenido en el Paso III.
Determinación de la presencia de movimientos periódicos (C)
Conocida la ecuación de tendencia y el índice de estacionalidad, se determina el aporte conjunto a la serie de los movimientos periódicos e irregulares, despejando en la ecuación del modelo el producto C*I o la suma C+I, en dependencia del modelo escogido como se indica en las ecuaciones siguientes:
C + I = y - T -S
![]()
A la serie de datos transformada (C + I ó C*I), se le aplica una media móvil de orden 3, 5, 7, etc. y se grafica el resultado hasta que la existencia o ausencia de movimientos cíclicos sea evidente. En caso afirmativo, se selecciona la media móvil que permita la caracterización de éste, es decir, brinde la posibilidad de obtener una dependencia funcional que describa el comportamiento de C.
Debe señalarse que, atendiendo a la diversidad de comportamientos que pueden existir en la práctica no es posible elaborar una metodología de carácter general para la obtención de un modelo analítico que caracterice a este movimiento y puede requerir de una cierta cantidad de pruebas para lograr un modelo que exhiba un ajuste adecuado.
Determinación de la aparición de movimientos irregulares (I)
Conocidos los estimadores de tendencia, estacionalidad y periodicidad, se determina el aporte total a la serie del movimiento irregular en cada periodo, despejando I en el modelo escogido (aditivo o multiplicativo), como se indica en las siguientes expresiones:
I = y - T - S - C
![]()
Ejemplo de una Serie Cronológica
Planes antiguos:
1º) Si los índices de variación estacional en los tres primeros meses del año son 100, 90 y 105, y la tendencia secular de esta serie histórica es
t= a + 12 t, calcular las variaciones cíclicas si los datos del trimestre son 20, 22 y 28
Solución
Método Gráfico
Mediante este método muy elemental se determina la tendencia a partir de una representación gráfica de la serie. La aplicación de este método es como sigue:
-
Se representa gráficamente la serie cronológica
-
Se unen los extremos superiores de la serie, se hace lo mismo con los inferiores
-
Se obtiene dos líneas que encierran a la serie original
-
Uniendo los puntos medios de las distancias entre las dos líneas o curvas se obtiene la tendencia. La línea o curva de tendencia obtenida tendrá un trazado mucho más suave que la serie original.

Fig. 7 Representación tendencia estacionaria
Método de las medias móviles
Para este método se deben de considerar los siguientes pasos que se detallan
-
Observar con detenimiento la serie para determinar aproximadamente la fluctuación con periodo mas largo y llamamos “q” al número de observaciones que forman una oscilación compleja.
-
Se procede a calcular una serie de medias. La primera de ellas se calcula a partir de las primeras observaciones de la serie pero eliminando la primera observación y añadiendo al inmediato posterior. Se prosigue así hasta calcular la media de la últimas “q” observaciones.
-
Cada una de las medias obtenidas en el paso anterior se asigna al instante o momento del período temporal que promedian.
-
Uniendo las medias se obtiene la tendencia.
Aplicación
Caso 1: Producción de Motocicletas en una empresa japonesa, periodo 1974 - 1990
En la siguiente tabla se tiene la producción de motocicletas de una empresa (en millones de motos) en un periodo de 17 años que se muestra en la tabla Nº 1
Tabla Nº1
Venta de Motocicletas en un periodo de 17 años
(Producción en millones de motocicletas)
| Años | Producción | Años | Producción | Años | Producción | ||
| 1974 | 2.1 | 1980 | 2.2 | 1986 | 2.1 | ||
| 1975 | 1.9 | 1981 | 2.0 | 1987 | 1.9 | ||
| 1976 | 1.7 | 1982 | 1.8 | 1988 | 1.5 | ||
| 1977 | 1.5 | 1983 | 1.7 | 1989 | 1.4 | ||
| 1978 | 1.6 | 1984 | 1.9 | 1990 | 2.5 | ||
| 1979 | 2.0 | 1985 | 2.4 | ---- | ----- |
Se traslada los datos a Microsoft Excel, ordenados en dos columnas, luego se realiza la gráfica de los datos.
Se obtiene la gráfica mostrada en la fig.8

Fig. 8 Representación de la serie de tiempo para las motocicletas por año
En la grafica se observa que los años donde se registra mayor producción son 1974, 1980, 1985,1990
Entonces podemos tomar cada cinco años como la cantidad de años para la cual la empresa realiza su mayor producción.
Sin embargo es conveniente encontrar una línea de tendencia tal que se pueda hallar una ecuación ajustada para los pronósticos de la producción en el tiempo.
Utilizando el método de la media móvil
Se construye una nueva tabla con las medias móviles
Esto es para suavizar la distribución de puntos

Fig. 9 Serie original y serie suavizada por los promedios móviles
Hallando la línea de tendencia
En Microsoft Excel, la línea de tendencia para la curva suavizada se obtiene fácilmente y se nuestra en la fig 10

Fig. 10. Línea de tendencia con R2 = 0.4169
El coeficiente de determinación es muy pequeño por lo que no se puede asegurar categóricamente que la ecuación lineal hallada es la que pronostica la producción en los años posteriores.
Será necesario realizar un segundo arreglo con medias móviles
El problema ahora es que el período donde alcanza la mayor producción es un número par de años, por lo que se hace difícil en la tabla hallar el año central.

Fig.11 Línea de tendencia por segunda vez
La fig. 11 muestra la segunda suavizada de la línea de tendencia, no ha variado mucho con respecto a la primera.
CONCLUSION
Las series cronológicas o temporales pueden servir para predecir acontecimientos futuros en base a ciertos comportamientos de determinadas variables. Si tenemos mas observaciones que se puedan promediar, que es el orden de la media móvil, se obtienen tendencias mas suaves. Con el procedimiento de medias móviles siempre es posible elegir el número de observaciones que se deben tomar para el promedio, esto no siempre es fácil, esto da el período de oscilación. Si se determina la función matemática de la tendencia lineal, esta no permitirá conocer los valores perdidos tanto al inicio como al final del proceso de búsqueda de la línea de tendencia.
14
Serie Eliminación de la tendencia Serie desestacionalizada
20 20 20
21x100
= 23.33
22 22-1= 21 90
26 x 100
28 28-2= 26 105 = 24.76
Descargar
| Enviado por: | Lilicar |
| Idioma: | castellano |
| País: | Venezuela |
