Informática
Resolución del comportamiento de un mecanismo por Newton-Raphson
Análisis Numérico
Resolución del Comportamiento de un
Mecanismo por Newton-Raphson
Búsqueda de Raices
Objetivo:
Usando un método para encontrar raíces en una función, se resolverá un problema de un mecanismo. Usando el método de Newton-Raphson y usando una ecuación que describe el comportamiento de un mecanismo, encontraremos los valores adecuados en un intervalo. Usando el entorno de programación QBasic, se hizo un programa que calcula de manera rápida y fácil las raíces esperadas.
Marco Teórico:
Tal vez, dentro de las fórmulas para localizar raíces, la fórmula de Newton-Raphson sea la más ampliamente usada, Si el valor inicia de la raíz es Xi, entonces se puede extender una tangente desde el punto (xi, f(xi)). El punto donde esta tangente cruza al eje x, representa una aproximación mejorada de la raíz.
El método Newton-Raphson se puede obtener sobre la base de una interpretación geométrica (un método alterno basado en la serie de Talyor), Podemos obtener una ecuación general para la forma, la cual nos queda:
X i+1 = Xi - (f(Xi) / f'(Xi))
Cómo con los otros métodos de localización de raíces, la ecuación de Newton-Raphson se puede usar como un criterio de paro. Además, el desarrollo del método con base en la serie de Taylor proporciona un conocimiento teórico relacionado con la velocidad de convergencia expresado como: Ei +1 n= O(E2i).
De esta forma, el error debe ser casi proporcional al cuadrado del error anterior.
El algoritmo del método de Newton-Raphson se obtiene al sustituir la ecuación principal con la fórmula predictiva. Obsérvese, sin embargo, que el programa también debe modificarse para calcular la primera derivada. Esto se puede llevar a cabo simplemente incluyendo una función definida por el usuario.
Además, de acuerdo con las discusiones anteriores sobre los problemas potenciales del método d Newton-Raphson, el programa se podría mejorar al incorporar algunas consideraciones adicionales:
1.- Si es posible, se debe incluir una rutina de graficación dentro del programa.
2.- Al final de los cálculos, la raíz final calculada debería siempre ser sustituida en la función original para calcular en qué casos el resultado se acerca a cero. Esta prueba protege contra aquellos casos en los que se observa convergencia lenta u oscilatoria, la cual puede llevar a valores pequeños de error, mientras que la solución puede estar aún muy lejos de una raiz.
3.- El programa debería siempre incluir un límite máximo sobre el número permitido de iteraciones para estar prevenidos contra las oscilaciones y la convergencia lenta, o en caso contrario las soluciones divergentes persistirán en forma interminable.
4.- El programa debería alertar al usuario y tomar en cuenta la posibilidad de que f'(x) pueda ser cero en cualquier momento durante el cálculo.
Descripción del Problema
LA figura mostrada es la gráfica de la función cúbica de la ecuación mostrada. Se hará un programa para investigar el comportamiento del algoritmo de Newton-Raphson conforme dos valores iniciales dados. Uno es 1.8 y el otro 2.5. Se debe determinar el valor para el cual la convergencia cambia de raíces, siendo el incremento de 0.1. La gráfica y la función son las siguientes:
Y = f(x) = -X3 - 2x2 + 50x + 60
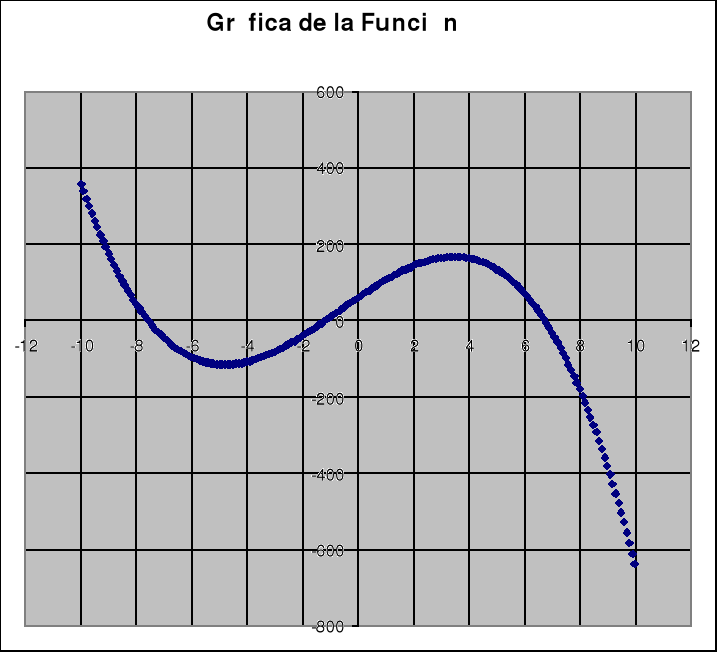
Así tenemos una función igualada que podemos igualar a cero con una sola variable, y ya se puede usar el método de Newton-Raphson para encontrar los valores de esta variable en el rango que yo quiera. Entonces es aquí donde utilizo el programa en QBasic. El código del programa se presenta a continuación,
Código del Programa
CLS
PRINT " Programa para obtener TODAS las raíces"
PRINT " de una ecuación en función de x"
PRINT " METODO DE NEWTON RAPHSON"
INPUT " Escribe cuántas cifras significativas "; Cif
INPUT " Escribe la frontera izquierda x "; FI
INPUT " Escribe la frontera derecha x "; FD
INPUT " Escribe el diferencial a usar "; Dif
PRINT " Las raíces de la ecuación son:"
ES = .5 * 10 ^ (2 - Cif)
a = FI
r = 0
`y = -(x ^ 3) - (2 * (x ^ 2)) + (50 * x) + 60
DO
c = 0
b = a + Dif
FA = -(a ^ 3) - (2 * (a ^ 2)) + (50 * a) + 60
FB = -(b ^ 3) - (2 * (b ^ 2)) + (50 * b) + 60
IF FA = 0 THEN
PRINT SPACE$(25); a
r = r + 1
c = 1
ELSE
IF FB = 0 THEN
PRINT SPACE$(25); b
r = r + 1
c = 1
END IF
END IF
IF (FA * FB) < 0 AND c = 0 THEN
m = a
DO
FM = -(m ^ 3) - (2 * (m ^ 2)) + (50 * m) + 60
DFM = -(3 * (m ^ 2)) - (4 * m) + 50
m2 = m - (FM / DFM)
FM2 = -(m2 ^ 3) - (2 * (m2 ^ 2)) + (50 * m2) + 60
IF ABS(FM2) < (1 / (10 ^ Cif)) THEN
PRINT SPACE$(25); m2
r = r + 1
c = 1
ELSE
EA = ABS((m2 - m) / m2) * 100
IF EA < ES THEN
PRINT SPACE$(25); m
r = r + 1
c = 1
ELSE
m = m2
END IF
END IF
LOOP UNTIL c = 1
END IF
a = b
LOOP WHILE a < FD
IF r = 0 THEN PRINT SPACE$(20) + "No se pudo encontrar raíces." ELSE PRINT SPACE$(20) + "Son todas."
Se notará que el programa ya tiene como función la derivada de la ecuación original. Se está usando un intervalo de -10 a 10, ya que los dos valores iniciales propuestos están dentro de este rango. Corriendo el programa, los valores obtenidos son:
-7.562 -1.777 y 6.740
Conclusiones:
Es bastante fácil encontrar estos valores con un algoritmo hecho en la computadora. Nada más se dan los datos requeridos y la máquina hace todo. Con este métodos se puede encontrar fácilmente el comportamiento de un mecanismo, dada una ecuación. Facilita mucho los cálculos.
Bibliografía:
Métodos Numéricos para Ingenieros.
STEVEN CHAPRA
Ed. McGraw Hill
Diseño de Maquinaria.
ROBERT L. NORTON
Ed. McGraw Hill
Descargar
| Enviado por: | Esqueda |
| Idioma: | castellano |
| País: | México |
