Informática
Programación
![]()
Manual para la asignatura
ELEMENTOS DE PROGRAMACIÓN
Programa de Estudios:
INGENIERÍA EN GESTIÓN INFORMÁTICA
ANALISTA PROGRAMADOR
MARZO DEL 2002
i. Introducción
El objetivo de la asignatura “Elementos de Programación” es introducir en forma progresiva y sistemática una correcta metodología para que los alumnos de la Carrera Ingeniería en Gestión Informática dominen las técnicas de la programación de computadores.
Este manual esta confeccionado con el propósito de servir de guía para el desarrollo de la asignatura. Las materias aquí tratadas corresponden a lo indicado en el Programa Oficial de Inacap por lo que deberán ser tratadas en clases en su totalidad y siguiendo los lineamientos que aquí se indican.
De debe tener en cuenta que la Asignatura “Elementos de Programación” está orientada esencialmente a la metodología, por lo tanto, se persigue que el alumno adquiera los conocimientos necesarios para desarrollar programas utilizando métodos precisos, claros y eficientes.
La orientación de las técnicas de solución de problemas no debe estar orientada hacia ningún lenguaje de programación en especial.
ii. Estructura del manual
El manual está dividido en unidades. Al final de cada una de ellas se dejan algunos “Ejercicios propuestos” para entregárselos a los alumnos o desarrollarlos en clases
Con el objeto de estandarizar la nomenclatura utilizada en la resolución de problemas mediante un seudolenguaje único, se ha adoptado la siguiente nomenclatura:
-
Todas las palabras claves de los algoritmos están en ingles. Ejemplo : While, If, End, Read, Print, Open, Close, etc
-
Todas las variables deben ser declaradas. Se utilizan solamente dos tipos de variables: numéricas y alfanuméricas
El prefijo para declarar las variables numéricas es num y para las variables alfanuméricas, char. Se debe anteponer al nombre de la variable
Ejemplos
num x
char frase
-
La asignación de variable utiliza el símbolo
-
El signo igual sólo se debe utilizar para la igualdad
-
El índice menor de un arreglo es 1
-
Los comentarios se identifican anteponiendo el símbolo #
INDICE DE CONTENIDOS
UNIDAD 1: ANALISIS DE PROBLEMAS Y PROCESAMIENTO DE DATOS
1.1 RESOLVER PROBLEMAS GENERALES APLICANDO LA METODOLOGIA DE POLYA…………
1.1.1 Las estrategias de resolución de problemas
1.1.2 Metodología de resolución de problemas según Polya
1.1.3 Algunas sugerencias hechas por quienes tienen éxito en resolver problemas
1.2: CONCEPTO DE DATO E INFORMACIÓN……………………………………………………………….
UNIDAD 2: ALGORITMOS Y ESTRUCTURAS DE CONTROL
2.1 DESCRIBIR EL PROCESO DE CREACIÓN DE UN PROGRAMA PARA PROBLEMAS SIMPLES
2.1.1 Procesos de creación de programas
UNIDAD 1: ANALISIS DE PROBLEMAS Y PROCESAMIENTO DE DATOS
OBJETIVO 1.1: RESOLVER PROBLEMAS GENERALES APLICANDO LA
METODOLOGIA DE POLYA
Uno de los aspectos más importantes a considerar en el proceso de resolución de problemas es conseguir una representación mental del problema. Esto implica tener una visión general del problema y por ende, es mucho más fácil entender sus características y singularidades. Los datos importantes son identificados y relacionados entre si. Al modelado del problema se le llama también espacio del problema.
A continuación se presenta un ejemplo para ilustrar cómo se puede representar un problema en la memoria:
La tendencia más común es que la mayoría de los estudiantes puedan decir cuántas personas llegan a la parada final, cuántas subieron o cuántas bajaron, pero muy pocos están en condiciones de indicar cuántas paradas hay en la ruta del autobús debido a que seleccionaron la información numérica como datos importantes y la representaron internamente en la forma de operaciones aritméticas.
En términos de los procesos involucrados en la resolución de problemas, esto sucede porque la meta del problema no estaba bien definida a pesar de que había datos numéricos explícitos precisos. El énfasis sobre el número de personas que suben y bajan del autobús hace posible que los estudiantes piensen que tienen que hacer algo con esos datos y, en tal sentido, construyen una meta la cual se representa como el logro de una cantidad total. Esta decisión conduce a los estudiantes a seleccionar cierta información como relevante (número de personas que suben y bajan del autobús) e ignorar otra (número de paradas del autobús).
1.1.1 Las estrategias de resolución de problemas
Las estrategias para resolver problemas se refieren a las operaciones mentales utilizadas para pensar sobre la representación de las metas y los datos, con el fin de transformarlos para obtener una solución. Las estrategias para la resolución de problemas incluyen los métodos heurísticos, los algoritmos y los procesos de pensamiento divergente.
1.1.1.a Los métodos heurísticos
Son estrategias generales de resolución y reglas de decisión utilizadas por los solucionadores de problemas, basadas en la experiencia previa con problemas similares. Estas estrategias indican las vías o posibles enfoques a seguir para alcanzar una solución pero, no garantiza la solución del problema.
1.1.1.b Los algoritmos
Los algoritmos son procedimientos específicos que señalan paso a paso la solución de un problema y que garantizan el logro de una solución siempre y cuando sean relevantes al problema.
Un procedimiento algorítmico es una sucesión de acciones que hay que realizar, completamente prefijada y su correcta ejecución lleva a una solución segura del problema como, por ejemplo, realizar una raíz cuadrada, coser un botón, preparar una taza de café, hacer sopaipillas, etc. El algoritmo garantiza la obtención de lo que nos proponemos
De esta manera, el algoritmo se diferencia del heurístico en que este último constituye sólo “una buena apuesta”, ya que ofrece una probabilidad razonable de acercarnos a una solución. Por lo tanto, es aceptable que se utilicen los procedimientos heurísticos en vez de los algorítmicos cuando no conocemos la solución de un problema.
1.1.1.c Los procesos de pensamiento divergente
Los procesos de pensamiento divergente permiten la generación de enfoques alternativos a la solución de un problema y están relacionados principalmente con la inspiración y la creatividad.
La adquisición de habilidades para resolver problemas ha sido considerada como el aprendizaje de sistemas de producción que involucran tanto el conocimiento declarativo como el procedimental. Existen diversos procedimientos que pueden facilitar o inhibir la adquisición de habilidades para resolver problemas, entre los cuales se pueden mencionar:
-
Ofrecer representaciones metafóricas.
-
Permitir la verbalización durante la solución del problema.
-
Hacer preguntas.
-
Ofrecer ejemplos.
-
Ofrecer descripciones verbales.
-
Trabajar en grupo.
-
Utilizar auto-explicaciones.
METODOLOGIA DE RESOLUCIÓN DE PROBLEMAS SEGÚN POLYA.
Existen métodos bien definidos y desarrollados para lograr una resolución efectiva de problemas. Uno de estos métodos es el desarrollado por George Polya destacado Doctor en Matemática, nacido en Hungría en 1887, el que fue publicado inicialmente en la Universidad de Princeton en 1945 y finalmente en su libro "How to Solve It" en 1957.
Las sugerencias de Polya para responder a la pregunta ¿Cómo plantear y resolver problemas?, son las siguientes:
-
Entender el problema. (reconociendo qué se pregunta.)
-
Idear un plan. (respondiendo a lo que se pide.)
-
Realizar el plan. (desarrollando el resultado de la respuesta.)
-
Mirar hacia atrás. (controlando qué hace y dice el resultado)
1.1.2.a Entender el problema. Consiste en identificar qué se pide de modo completamente independiente de las diversas condiciones que pueden ser impuestas y limitaciones constatables en el problema.
Se deben considerar aspectos como:
-
¿Entiende todo lo que dice?
-
¿Puede replantear el problema en sus propias palabras?
-
¿Distingue cuáles son los datos?
-
¿Sabe a qué quiere llegar?
-
¿Hay suficiente información?
-
¿Hay información extraña?
-
¿Es este problema similar a algún otro que haya resuelto antes?
1.1.2.b Idear un plan. Consiste de responder tan directamente como sea posible lo qué se pide. Esto requiere generalmente uso de una ley, de una definición o de un principio que sea la respuesta a la pregunta hecha. Encontrar la conexión entre los datos y lo que se quiere. Puede verse obligado a considerar problemas auxiliares si una conexión inmediata no puede ser encontrada.
Se deben considerar aspectos como:
-
¿Ha visto el mismo problema en una forma levemente diferente?
-
¿Conoce algún problema relacionado?
-
Si está frente a algo completamente desconocido, intente pensar en un problema conocido que tenga alguna parte igual o similar.
-
Sí es un problema relacionado con otro solucionado antes. ¿Podría utilizarlo?. ¿Podría utilizar su resultado, su método?
-
¿Podría exponer el problema en forma modificada?
-
¿Se usaron todos los datos?
1.1.2.c Realizar el plan. Consiste en el responder a las peticiones hechas por el resultado del paso de progresión anterior. Esto puede derivar en un problema embutido que requiere el uso progresivo del primer, segundo y tercer paso.
Se deben considerar aspectos como:
-
Implementar la o las estrategias que se escogieron hasta solucionar completamente el problema o hasta que la misma acción sugiera tomar un nuevo curso.
-
Tomar un tiempo razonable para resolver el problema. Si no tiene éxito solicitar sugerencias o hacer el problema a un lado por un momento
-
No tener miedo de volver a empezar. Suele suceder que un comienzo fresco o una nueva estrategia conducen al éxito.
1.1.2.d El mirar hacia atrás. Consiste en varios chequeos, usando el sentido común, del resultado de usar los primeros tres pasos de progresión.
Se deben considerar aspectos como:
-
¿Está bien el resultado?
-
Es la solución correcta? ¿La respuesta satisface lo establecido en el problema?
-
¿Se advierte una solución más sencilla?
-
¿Puede ver cómo extender la solución a un caso general?
EJEMPLO Nº1:
A un empleado de una empresa se le cancela como Sueldo Base la cantidad de $520.000. ¿Cuál es el sueldo líquido del empleado si además, se le cancelará un bono equivalente al 20% de su Sueldo Base?
Entender el problema.
Leer cuidadosamente el problema.
Se desea obtener el sueldo líquido a pago de un empleado para lo cual se necesita conocer su sueldo base, el porcentaje del bono y alguna fórmula relacionada con el problema
Identificación de datos importantes.
Sueldo Base
Porcentaje del Bono
Sueldo Líquido
Idear un plan.
Determinar claramente lo que hay que hacer.
Es un problema conocido
Se utilizará la fórmula
Sueldo Líquido = Sueldo Base + Sueldo Base * 20%
Otra formula podría ser
Sueldo Líquido = Sueldo Base * 1,2
Una vez calculado, escribir el resultado.
Realizar el Plan
El 20% del Valor del Bono = 20/100
Monto del Bono = Sueldo Base * 20/100
Sueldo Líquido = Sueldo Base + Monto del Bono
Mirar hacia atrás
Verifique: Controlar la respuesta.
Sueldo base = 520.000
Monto del Bono = 520.000 * 20/100 = 104.000
Sueldo Líquido = 520.000 + 104.000 = 624.000
Respuesta: El sueldo líquido del empleado es de $624.000
EJEMPLO Nº2:
En una clase de 35 alumnos aprobaron el 40%. Determinar el número de alumnos reprobados.
Entender el problema.
Trazar un diagrama.
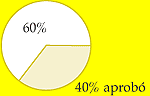
Identificación de datos importantes.
Total de alumnos: 35. Representan el 100%.
Total alumnos aprobados = 40% del Total de alumnos
Idear un plan.
Determinar claramente lo que hay que hacer.
Es un problema conocido
Al examinar el problema, lo podemos descomponer. El enunciado expresa que hay que determinar el número de alumnos reprobados, pero como sabemos que los aprobados y los reprobados representan la totalidad del curso, podemos resolver el problema de dos formas.
-
Forma 1. Transformar el 40% de aprobados en número de alumnos utilizando una operación sencilla y restárselo al total de alumnos.
-
Forma 2. Transformar el 60% de reprobados en número de alumnos.
Llevado a notación algebraica:
Para la Forma 1:
35-------100%
X---------40%
Total de alumnos - x = Total de reprobados
Para la Forma 2:
35-------100%
X---------60%
x = Total de reprobados
Realizar el Plan
Para la Forma 1: X = (35 x 40) / 100 = 1.400 / 100 = 14
14 alumnos representan el 40% de los alumnos aprobados.
Por lo tanto, 35 - 14 = 21 alumnos reprobados
Para la Forma 2: X = (35 x 60) / 100 = 2.100 / 100 = 21
Mirar hacia atrás
Sumando los alumnos aprobados y reprobados debemos obtener el total de alumnos del curso. En efecto:
21 alumnos reprobados + 14 alumnos aprobados = 35 alumnos en el curso.
1.1.3 Algunas sugerencias hechas por quienes tienen éxito en resolver problemas:
Además del Método de Cuatro Pasos de Polya nos parece oportuno presentar en este apartado una lista de sugerencias hechas por personas exitosas en la solución de problemas:
Acepta el reto de resolver el problema.
Rescribe el problema en tus propias palabras.
Tómate tiempo para explorar, reflexionar, pensar...
Habla contigo mismo. Hazte cuantas preguntas creas necesarias.
Si es apropiado, trata el problema con números simples.
Muchos problemas requieren de un período de incubación. Si te sientes frustrado, no dudes en tomarte un descanso -el subconsciente se hará cargo-. Después inténtalo de nuevo.
Analiza el problema desde varios ángulos.
Revisa tu lista de estrategias para ver si una o más te pueden ayudar a empezar
Muchos problemas se pueden resolver de distintas formas: sólo se necesita encontrar una para tener éxito.
No tengas miedo de hacer cambios en las estrategias.
La experiencia en la solución de problemas es valiosísima. Trabaja con todos tus conocimientos, tu confianza crecerá.
Si no estás progresando mucho, no vaciles en volver al principio y asegurarte de que realmente entendiste el problema. Este proceso de revisión es a veces necesario hacerlo dos o tres veces, ya que la comprensión del problema aumenta a medida que se avanza en el trabajo de solución.
Siempre, siempre mira hacia atrás: Trata de establecer con precisión cuál fue el paso clave en tu solución.
Ten cuidado en dejar tu solución escrita con suficiente claridad de tal modo que puedas entenderla si la lees 10 años después.
Ayudar a que otros desarrollen habilidades en la solución de problemas es una gran ayuda para uno mismo: No les des soluciones; en su lugar provéelos con sugerencias importantes.
¡Disfrútalo! Resolver un problema es una experiencia significativa.
OBJETIVO 1.2: ANALIZAR UN PROCESO COMPUTACIONAL EN TERMINOS
DE ENTRADA - OPERACIÓN INTERNA - SALIDA
1.2.1 CONCEPTO DE DATO E INFORMACIÓN
Datos: Es todo aquella representación de una entidad y que es susceptible de tratamiento ya sea en un programa o proceso informático. Por ejemplo nombre, apellido y edad son datos de una persona (entidad).
En otras palabras un dato es la representación de una realidad.
Información: Mensaje valido para un receptor o resultado del procesamiento de datos.
Computador: Máquina capaz de aceptar datos de entrada, procesarlos y entregar resultados de salida (información).
Esquema general de un computador
Programa (software): Conjunto de órdenes o instrucciones capaces de manipular un conjunto de datos. Estas órdenes pueden ser divididas en tres grandes bloques claramente diferenciales, estos son:
-
Entrada de datos: En este bloque se engloban todas aquellas instrucciones que toman datos de un dispositivo o periférico externo, depositándolos en la memoria principal del computador para ser procesados.
-
Proceso: Engloban todas aquellas instrucciones encargadas de modificar los datos que previamente habían sido depositados en a memoria principal. Todos los resultados obtenidos en el tratamiento de dichos datos son depositados nuevamente en la memoria principal quedando de esta manera disponible.
-
Salida de resultados: Es el conjunto de instrucciones que toman los resultados finales desde la memoria principal y lo envían a dispositivos externos.
Ejercicios propuestos
Crear grupos de trabajos de 6 integrantes. Para los ejercicios propuestos, los alumnos deberán determinar sin existen datos de entrada y cuales son, que procesos se realizan sobre ellos y cuales son los datos de salida.
Determinar el promedio de edad entre los integrantes del grupo.
Determinar la cantidad de mujeres y la cantidad de hombres dentro del grupo.
Contar los alumnos que son mayores de edad (18 años o más) y menor de edad (inferior a 18 años), en el grupo.
Determinar la cantidad de integrantes que salieron de cuarto medio con un promedio igual o inferior a 5.0.
Solución esperada
1a. Datos de entrada = Cantidad de personas. Edades de las personas
Procesamiento = Sumar las edades y dividirla por la cantidad de
personas.
Datos de salida = Promedio de edad de todas las personas del grupo.
1b. Datos de entrada = Personas del grupo.
Procesamiento = Contar las mujeres. Contar los hombres.
Datos de salida = Cantidad de mujeres y hombres.
1c. Datos de entrada = Edades de los alumnos del grupo.
Procesamiento = Cada edad comparar con 18. Contar los menores a 18 años. Contar los que tienen 18 o más años en forma separada.
Datos de salida = Cantidad de mayores de edad. Cantidad de menores
de edad..
1d. Datos de entrada = Notas de egreso de 4º Medio
Procesamiento = Cada nota comparar con 5.0. Contar las menores o iguales a 5.0.
Datos de salida = Cantidad de personas que salieron de 4º Medio con nota promedio igual o menor a 5.0
Para las siguientes situaciones identificar: datos, proceso y resultado (información).
El promedio de las edades de los 30 alumnos de un curso es de 22 años.
Datos: ______________________________________________
Proceso: ______________________________________________
Información: ______________________________________________
En una agroindustria a un productor por 2 toneladas de harina se le cancelaron 4 millones de peso.
Datos: ______________________________________________
Proceso: ______________________________________________
Información: ______________________________________________
Para cercar un jardín de 3 metros de largo por 5 metros de ancho se necesitaron 16 metros de alambre.
Datos: ______________________________________________
Proceso: ______________________________________________
Información: ______________________________________________
UNIDAD 2: ALGORITMOS Y ESTRUCTURAS DE CONTROL
OBJETIVO 2.1: DESCRIBIR EL PROCESO DE CREACIÓN DE UN PROGRAMA
PARA PROBLEMAS SIMPLES
2.1.1 PROCESOS DE CREACIÓN DE PROGRAMAS.
Programa: Conjunto de instrucciones escritas de algún lenguaje de programación y que ejecutadas secuencialmente resuelven un problema especifico. Todo programa debe pasar por fases de elaboración hasta llegar al producto final.
Resolvemos problemas a diario, pero normalmente ignoramos el proceso que estamos siguiendo. La mayoría de nuestra experiencia es simplemente seguir algoritmos, recetas. Por ejemplo: practicamos un juego, preparamos café, caminamos, etc.
Etapas en el proceso de resolución de problemas
Para aprender a programar hay que desarrollar en forma consciente alguna estrategia de resolución de problemas.
Algunas de las etapas que se deben seguir en este proceso son:
Diseño del proceso: Esta etapa consiste en el análisis del problema, esto es: entender el problema, determinar estrategias de solución. En ambos casos se indicará claramente los procesos a seguir (lo que se va a hacer) para llegar a la solución correcta. En esta etapa además, se desarrolla un modelo que no es más que una representación apropiada al problema planteado. En otras palabras, se debe visualizar como se realizará la transformación de los datos de entrada para que a través de un proceso apropiado se obtenga la salida correcta.
Construcción: Esta etapa consiste en desarrollar un algoritmo que pueda representar la estructura del programa la cual puede ser en forma narrativa, diagramas de flujo o Pseudolenguaje.
Codificación: Consiste en la traducción del algoritmo a algún lenguaje de programación, el cual crea instrucciones entendibles y ejecutables por el computador; algunos de estos lenguajes pueden ser Pascal, C, C++, Visual Basic, Java, etc.
Verificación: Se prueba el algoritmo en forma analítica para demostrar la efectividad del algoritmo; vale decir, se prueba el algoritmo y/o programa con datos conocidos que producirán una salida conocida. Con esto se pretende detectar y corregir los errores para mejorar el programa o algoritmo.
Documentación: En esta etapa se debe documentar el o los programas realizados en la etapa de construcción. Se debe confeccionar un manual de uso que contenga, al menos los siguientes puntos:
-
Descripción del método de solución utilizado
-
Requerimientos lógicos (Sistema Operativo, Software, etc.).
-
Requerimientos físicos (Servidores, computadores, periféricos, etc)
Características mínimas de los programas
Para asegurar la calidad de los programas y sistemas de desarrollo, es de vital importancia, considerando que para un problemas existen muchas soluciones, elegir la alternativa mas eficaz y eficiente en función del problema dado. Todo programa debe cumplir al menos con las siguientes características:
Legibilidad: Claro y sencillo para una fácil lectura y comprensión.
Modificabilidad: El programa para su vigencia y actualización, debe ser de fácil mantenimiento.
Fiabilidad: Debe ser robusto, fácil de recuperarse frente a errores o malos usos
Eficiencia: Eficiente, aprovechando al máximo los recursos.
Portabilidad: El programa debe ser de fácil codificación para distintos lenguajes.
Ejercicios
Para las siguientes situaciones identifique la etapa o fase del proceso en la resolución de un programa.
El algoritmo creado se traducirá en lenguaje C++.
Etapa _______________________________________________________
Algoritmo requiere de una formula que calcule el volumen de un prisma.
Etapa _______________________________________________________
La resolución de un problema ha sido escrita en forma narrativa.
Etapa _______________________________________________________
Un algoritmo ha sido recorrido con datos conocidos.
Etapa _______________________________________________________
Solución esperada
Etapa de Codificación
Diseño
Construcción
Verificación
OBJETIVO 2.2: EXPLICAR LOS PRINCIPIOS QUE RIGEN EL ALMACENAMIENTO
DE DATOS
2.2.1 UNIDADES FUNCIONALES DE UN COMPUTADOR
Organización física de un computador
Dispositivos de Entrada: Como su nombre lo indica, sirven para introducir datos al computador para su proceso. Los datos se leen de los dispositivos de entrada y se almacenan en la memoria central o interna. Ejemplos: teclado, scanners, mouse, joystick, lápiz óptico, etc.
La Unidad Central de Procesamiento (C.P.U) se divide en dos:
Unidad de Control: Coordina las actividades de la computadora y determina que operaciones se deben realizar y en que orden; así mismo controla todo el proceso de la computadora.
Unidad Aritmético - Lógica: Realiza operaciones aritméticas y lógicas, tales como suma, resta, multiplicación, división y comparaciones.
Dispositivos de Salida: Regresan los datos procesados que sirven de información al usuario. Ejemplo: monitor, impresora.
2.2.2 PRINCIPIOS DE ALMACENAMIENTO
La memoria de la computadora se divide en dos:
-
Memoria Central o Interna
-
Memoria Auxiliar o Externa
Memoria Central o interna: La CPU utiliza la memoria del computador para guardar información mientras trabaja. Mientras esta información permanece en memoria, el computador puede tener acceso a ella en forma directa. La memoria interna consta de dos áreas de memoria:
-
La memoria RAM (Random Access Memory): Recibe también el nombre de memoria principal o memoria de usuario, en ella se almacena información sólo mientras el computador este encendido. Cuando el computador se apaga o arranca nuevamente, la información se pierde, por lo que se dice que la memoria RAM es una memoria volátil.
-
La memoria ROM (Read Only Memory): Es una memoria estática que no puede cambiar, el computador puede leer los datos almacenados en la memoria ROM, pero no se pueden introducir datos en ella, o cambiar los datos que ahí se encuentran; por lo que se dice que esta memoria es de sólo lectura. Los datos de la memoria ROM están grabados en forma permanente y son introducidos por el fabricante del computador.
Memoria Auxiliar (Externa): Es donde se almacenan todos los programas o datos que el usuario desee. Los dispositivos de almacenamiento o memorias auxiliares (externas o secundarias) más comúnmente utilizados son: cintas magnéticas, discos magnéticos discos ópticos, disquetes.
Dirección y contenido de Memoria:
La dirección de memoria es un número que identifica un lugar dentro de la memoria. El contenido es lo que se encuentra dentro de una dirección.
Como analogía podemos pensar que direccion de memoria se asemeja al número que identifica a las casillas de correos y el contenido es lo que tienen adentro cada una de esas casillas.
Ejercicios:
La siguiente ilustración es una representación conceptual de una memoria, cuyas direcciones están representadas por variables (X,R,Y,etc) y los contenidos son los que se muestran.
| X 3 | R 12 | Y 4 | S -9 | L 100 | P 8 |
| T 100 | G 6 | A 20 | J 5 | W 80 | Z 5 |
Determinar los valores finales de los contenidos si se ejecutan secuencialmente las siguientes operaciones matemáticas.
XG+5
WA*X
TS+P-J
JT+L
ZP*R+Y
YY+Z
YY+1
Escriba en la siguiente ilustración los valores finales de las variables
| X | R | Y | S | L | P |
| T | G | A | J | W | Z |
La siguiente ilustración es una representación conceptual de una memoria, cuyas direcciones están representadas por variables (X,R,Y,etc) y los contenidos son los que se muestran.
| X 14 | R 8 | Y 0 | S -9 | L 130 | P 0 |
| T 16 | G -56 | A -4 | J 5 | W -8 | Z 0 |
Determinar los valores finales de los contenidos si se ejecutan secuencialmente las siguientes operaciones matemáticas.
XX+A-W
SX-J*Z
RR+1
YR-X+2
LY+L
TG+J-Z*3
WW+5
JJ+Z/X+2
Escriba en la siguiente ilustración los valores finales de las variables
| X | R | Y | S | L | P |
| T | G | A | J | W | Z |
Para las siguientes situaciones identifique la etapa o fase del proceso en la resolución de un programa.
Para un problema dado, que haremos para llegar a una solución correcta:
Etapa _______________________________________________________
Al recorrer el algoritmo que algunos datos el resultado no es el esperado:
Etapa _______________________________________________________
Un algoritmo será traducido a lenguaje Pascal:
Etapa _______________________________________________________
Un algoritmo calcula el área de un cuadrado para un valor cualquiera del lado:
Etapa _______________________________________________________
Al parecer el modelo matemático escogido soluciona el problema sólo para un tipo de datos:
Etapa _______________________________________________________
OBJETIVOS 2.3: DESCRIBIR A TRAVÉS DE DEFINICIONES Y EJEMPLOS CADA
UNO DE LOS ELEMENTOS QUE COMPONEN UN ALGORITMO
2.3.1 CONCEPTO DE ALGORITMO
La palabra algoritmo se deriva de la traducción al latín de la palabra árabe alkhowarizmi, nombre de un matemático y astrónomo árabe que escribió un tratado sobre manipulación de números y ecuaciones en el siglo IX.
Un algoritmo es una serie de pasos organizados que describe el proceso que se debe seguir para dar solución a un problema específico.
Tipos de Algoritmos
-
Cualitativos: Son aquellos en los que se describen los pasos utilizando palabras.
-
Cuantitativos: Son aquellos en los que se utilizan cálculos numéricos para definir los pasos del proceso.
Lenguajes Algorítmicos. Es una serie de símbolos y reglas que se utilizan para describir de manera explícita un proceso. Hay dos tipos:
-
Gráficos: Es la representación gráfica de las operaciones que realiza un algoritmo (diagrama de flujo).
-
No Gráficos: Representa en forma descriptiva las operaciones que debe realizar un algoritmo (pseudocódigo).
2.3.2 ESTRUCTURA DE UN ALGORITMO.
Las características de un buen algoritmo son:
-
Debe tener un punto único de inicio.
-
Debe ser definido, no debe permitir dobles interpretaciones.
-
Debe ser general, es decir, soportar la mayoría de las variantes que se puedan presentar en la definición del problema.
-
Debe ser finito en tamaño y tiempo de ejecución. Es decir, debe tener un fin.
Ejercicios
Presentar y discutir el siguiente ejercicio:
Se desea construir un algoritmo que cambie la rueda de un automóvil. La siguiente lista de paso le ayudará a en la construcción del algoritmo pero, para ello debe ordenarlas en una secuencia lógica.
a) Sacar las tuercas b) Inicio
c) Bajar el auto d) Colocar rueda de repuesto
e) Sacar herramientas y repuesto. F) Cerrar maletera
g) Colocar tuercas h) Fin
i) Abrir maletera j) Apretar tuercas
k) Posicionar gata y levantar el auto l) Guardar herramientas y rueda
m) Retirar rueda mala n) Soltar tuercas
Solución: b, i, e f, k, n, a, m, d, g, j, c, i, l, f, h
Presentar y discutir el siguiente ejercicio:
Solicitar que un alumno del curso haga la representación de un robot. Otro alumno le dará instrucciones para caminar desde su puesto hacia la puerta de la sala.
Algunos supuestos:
-
El alumno robot escucha y entiende instrucciones
-
El proceso “mover el pie” implica todos los subprocesos involucrados como, levantar la pierna, flectar las rodillas, mover dedos, etc.
Las instrucciones deberán ser del tipo:
-
Mover pie derecho hacia delante
-
Mover pie izquierdo hacia delante
-
Detenerse
-
Girar izquierda x grados
-
Girar derecha x grados
Dejar como tarea o resolver en clases algunos de los siguientes problemas cotidianos.
Cambiar las cuatro ruedas de un vehículo.
Preparar una taza de café
Tomar la micro desde la casa hasta la sede
OBJETIVO 2.4: REPRESENTAR GRAFICAMENTE LA CIRCULACION DE DATOS E
INFORMACIÓN Y LA SECUENCIA DE OPERACIONES
INVOLUCRADAS EN UN ALGORITMO DADO.
2.4.1 DEFINICION DE DIAGRAMA DE FLUJO
Para el diseño de algoritmos se utilizan técnicas de representación. Una de estas técnicas son los Diagramas de Flujo (DDF), que se definen como la representación gráfica que mediante el uso de símbolos estándar unidos mediante líneas de flujo, muestran la secuencia lógica de las operaciones o acciones que debe realizar un computador, así como la corriente o flujo de datos en la resolución de problema.
2.4.2 SIMBOLOGIA DE DIAGRAMA DE FLUJO
Algunos símbolos que se utilizan para desarrollar algoritmos en DDF son:
| Símbolo | Función |
| Terminal. Marca el inicio y/o el final en la ejecución de un DDF | |
| Operación de E/S en general. Se utiliza para la introducción de datos desde un periférico a la memoria del computador y para la salida de resultados desde la memoria del computador a un periférico. | |
| Proceso en general. Utilizado para mostrar cualquier tipo de operación durante el proceso de elaboración de los datos depositados en la memoria. | |
|
| Decisión de dos salidas, indica operaciones lógicas o comparativas seleccionando la ruta en función del resultado (si, no). |
| Indicadores de la dirección del flujo de datos | |
| Conector. Este símbolo es utilizado para el reagrupamiento de líneas de flujo. |
| OPERACIONES BASICAS PARA ALGORITMOS | |
| Asignación: Permite depositar valores o resultados de expresiones en una variable. Variable Expresión o valor | Asignación: |
| Leer Variable: Toma uno o varios datos desde un dispositivo de entrada para almacenarlos en variables Read Variable | Leer Variable: |
| Escribir Expresión: Imprime datos en los dispositivos externos, como impresora o pantalla Print Expresión o variable | Escribir Expresión : |
| Procesos : Instrucciones que modifican las variables a partir de un estado inicial hasta un estado final. p1; p2; p3; …; pn | Procesos : |
Algunas recomendaciones para el diseño de Diagramas de Flujo
No deben quedar líneas de flujo sin conectar.
Se deben trazar los símbolos de manera que se puedan leer de arriba hacia abajo y de izquierda a derecha.
Todo texto escrito dentro de un símbolo deberá ser escrito claramente, evitando el uso de muchas palabras.
Se deben usar solamente líneas de flujo horizontales y/o verticales.
Se debe evitar el cruce de líneas utilizando los conectores.
Se deben usar conectores sólo cuando sea necesario.
Ejemplos de desarrollo de algoritmos utilizando Diagramas de Flujo
Ejemplo Nº1
Algoritmo que permite calcular el área de un triangulo. Recordemos que la formula es Área = (Base * Altura) / 2.
Solución
Ejemplo Nº2
Algoritmo que captura tres notas y saca el promedio. Si el promedio es menor a 4.0 imprimir “Reprobado” caso contrario imprimir “Aprobado”
Solución
Ejemplo Nº3
Algoritmo que calcula la edad de una persona conociendo el año de nacimiento y el año actual.
Solución
Ejemplo Nº4
Hacer un DDF que verifique si un número es positivo, negativo o cero.
Solución
Ejemplo Nº5
Hacer un DDF para determinar el porcentaje de personas, de un grupo, que son mayores de edad (edad mayor o igual a 18 años).
Solución
Ejemplo Nº6
Hacer un DDF para determinar la cantidad de números pares en los primeros 50.000 números naturales. (Incluidos el 1 y el 50.000). Nótese que aquí se incorpora el concepto de declaración de variable e inicialización
Solución
Ejemplo Nº7
Hacer un DDF que permita calcular la edad actual de una persona en cualquier año conociendo la edad que la persona tiene en ese año. Por ejemplo, saber que edad actual tiene una persona sabiendo que para el 2010 tendrá 9 años. Se debe ingresar también el año actual
Solución
Ejemplo Nº8
Hacer un DDF que permita determinar la cantidad de números impares entre dos números naturales dados. No debe incluir los números dados
Ejercicios propuestos (OBJETIVO 2.4)
Crear un algoritmo DDF que al leer un número entero positivo (asuma que el número cumple las condiciones), imprima la palabra “PAR” si el número es par e “IMPAR” si es impar.
Supongamos que el IPC de los meses de Febrero y Marzo fueron 0.3% y 0.6% respectivamente. Crear un algoritmo en DDF que muestre el valor de un producto actualizado y la diferencia de precio entre el mes de Febrero y Marzo.
Confeccione un algoritmo en diagrama de flujo que al leer el neto de una factura, calcule el IVA y de cómo salida el total de la factura.
Crear un algoritmo en diagrama de flujo que al ingresar dos números imprima el mayor de ellos o IGUALES si son iguales.
Confeccionar un algoritmo en diagrama de flujo que imprima el salario reajustado de un trabajador según las siguientes categorías.
Cat1 20%
Cat2 15%
Cat3 .10%
Cat4 8%
Recorrer el siguiente DDF e indicar que es lo que hace
Haga el ruteo con los siguientes valores.
| e | Salida |
| 28 | |
| 15 | |
| 21 | |
| 14 |
INACAP Dirección de Área Informática
Versión 3.0 30 Elementos de Programación
Start
Un autobús parte del terminal en la mañana. Se detiene en la primera parada y recoge 5 personas. Sigue hasta la próxima parada y allí suben 6 personas. Continúa hasta la siguiente parada y suben 4 personas. En la próxima parada, suben 5 personas y se bajan 3. En la siguiente parada, suben 5 personas y se bajan 4. En la parada siguiente, suben 6 personas y se baja 1. La próxima vez, suben 3 personas y se bajan 2. La vez siguiente, se bajan 2 personas y no sube nadie. En la siguiente parada nadie espera por el autobús, de manera tal que este no se detiene. Finalmente, el autobús llega al terminal.
¿Cuántas paradas hay en la ruta del autobús?
Num inicio
Num final
Num e
Char X
DISPOSITIVO
DE
SALIDA
PROCESAMIENT0
DISPOSITIVO
DE
ENTRADA
no
No
no
Print Edad
si
si
No
No
Si
No
p1; p2; p3; …; pn
Print Expresión o variable
CPU
Dispositivo
de Entrada
Unidad de Control
Unidad
Arit.-Log
Memoria
Dispositivo
de Salida
Read Variable
Variable Expresión o valor
X”Adolescente”
X”Infantil”
Start
Read Base
Read Altura
Area(Base*Altura)/2
Print Area
End
End
Start
Read X,Y,Z
P(x+y+z)/3
P<4.0
Print “Aprobado”
Print “Reprobado”
si
Start
Read e
e<15
si
e<21
Print x
X”Adulto”
End
Si
Si
Para verificar que DDF está lógicamente bien construido utilizamos datos de prueba. Consideremos X=4,5; Y= 5,0 ; Z=5,5. La suma es 15, por lo tanto en P queda un 5,0. Se imprimirá la palabra o string “Aprobado”
Para verificar el diagrama de flujo utilizamos datos de prueba. Consideremos Base = 5 y Altura = 8. El resultado es la impresión del valor de la variable Área que es 20
no
Num añoX
Num Edad
Num añoHoy
Num EdadHoyl
Read Edad
no
si
si
End
Print cuenta
Cuentacuenta+1
Inicio es divisible por 2?
Inicio<final
Inicioinicio+1
Read inicio
Read final
no
si
si
Start
Numenume+1
End
Print Cont
Cont Cont+1
Nume es divisible por 2 ?
Nume>50000
Num nume 1
Num Cont1
Start
EdadHoyEdad
Print EdadHoy
si
no
si
End
añoHoy = añoX
EdadHoyEdad-(añoHoy-añoX)
EdadHoyEdad+(añoHoy-añoX)
añoHoy > añoX
Read añoX
Read Edad
Read añoHoy
Start
si
si
Print “Número ingresado es negativo”
Print “Número ingresado es positivo”
EdadAño_actual - Año_Nac
Read Año_Actual
Read Año_Nac
Print “Número ingresado es cero”
No
No
End
Nu > 0
Nu = 0
Read Nu
Start
ContPer = ContPer + 1
No
Print Porce
End
Porce (Cont18 / NumPer)*100
ContPer = NumPer
Cont18 = Cont18 + 1
Read NumPer
Start
si
Edad >= 18
End
Descargar
| Enviado por: | Cristian P.b |
| Idioma: | castellano |
| País: | Chile |
