Matemáticas
Probabilidad
4.2 introducción
Si el único propósito del investigador es describir los resultados de un experimento concreto, los métodos analizados en los capítulos anteriores pueden considerarse suficientes. No obstante, si lo que se pretende es utilizar la información obtenida para extraer conclusiones generales sobre todos aquellos objetos del tipo de los que han sido estudiados, entonces estos métodos constituyen sólo el principio del análisis, y debe recurrirse a métodos de inferencia estadística, los cuales implican el uso inteligente de la teoría de la probabilidad.
Comenzamos este bloque interpretando la noción de probabilidad y la terminología subyacente a esta área de las matemáticas, ya que la probabilidad constituye por sí misma un concepto básico que refleja su relación con la faceta del mundo exterior que pretende estudiar: los fenómenos aleatorios, los cuales obedecen unas ciertas reglas de comportamiento. De alguna manera, el concepto de probabilidad, se relaciona o nos recuerda las propiedades de la frecuencia relativa.
A partir de ella, y junto con las definiciones de probabilidad condicionada y la de sucesos independientes, se deducen los teoremas fundamentales del Cálculo de Probabilidades.
Nos centraremos posteriormente en el eslabón que une la teoría de la probabilidad y la estadística aplicada: la noción de variable aleatoria, mostrando de esta manera, como puede emplearse la teoría de la probabilidad para sacar conclusiones precisas acerca de una población en base a una muestra extraída de ella, y que muchos de los estudios estadísticos son de hecho, estudio de las propiedades de una o más variables aleatorias.
Tal como hemos citado anteriormente, en las aplicaciones prácticas es importante poder describir los rasgos principales de una distribución, es decir, caracterizar los resultados del experimento aleatorio mediante unos parámetros. Llegamos así al estudio de las características asociadas a una variable aleatoria introduciendo los conceptos de esperanza y varianza matemática, relacionándolos con los conceptos de media y varianza de una variable estadística.
El cálculo de probabilidades nos suministra las reglas para el estudio de los experimentos aleatorios o de azar, constituyendo la base para la estadística inductiva o inferencial.
Para trabajar con el cálculo de probabilidades es necesario fijar previamente cierta terminología. Vamos a introducir parte de ella en las próximas líneas.
4.4 Experimentos y sucesos aleatorios
Diremos que un experimento es aleatorio si se verifican las siguientes condiciones:
1.
Se puede repetir indefinidamente, siempre en las mismas condiciones;
2.
Antes de realizarlo, no se puede predecir el resultado que se va a obtener;
3.
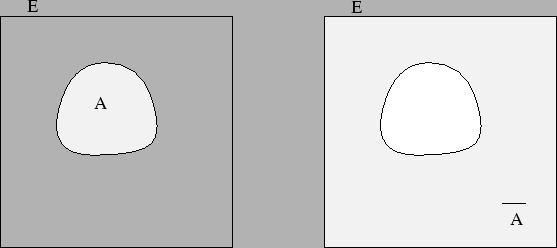
El resultado que se obtenga, e, pertenece a un conjunto conocido previamente de resultados posibles. A este conjunto, de resultados posibles, lo denominaremos espacio muestral y lo denotaremos normalmente mediante la letra E. Los elementos del espacio muestral se denominan sucesos elementales.
![]()
Cualquier subconjunto de E será denominado suceso aleatorio, y se denotará normalmente con las letras A, B,...
![]()
Obsérvese que los sucesos elementales son sucesos aleatorios compuestos por un sólo elemento. Por supuesto los sucesos aleatorios son más generales que los elementales, ya que son conjuntos que pueden contener no a uno sólo, sino a una infinidad de sucesos elementales --y también no contener ninguno.-- Sucesos aleatorios que aparecen con gran frecuencia en el cálculo de probabilidades son los siguientes:
4.4.0.0.0.1 Suceso seguro:
Es aquel que siempre se verifica después del experimento aleatorio, es decir, el mismo E
![]()
4.4.0.0.0.2 Suceso imposible:
Es aquel que nunca se verifica como resultado del experimento aleatorio. Como debe ser un subconjunto de E, la única posibilidad es que el suceso imposible sea el conjunto vacío
![]()
4.4.0.0.0.3 Suceso contrario a un suceso A:
También se denomina complementario de A y es el suceso que se verifica si, como resultado del experimento aleatorio, no se verifica A. Se acostumbra a denotar con el símbolo ![]()
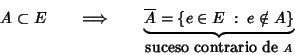
| Figura: Representación gráfica de un suceso aleatorio |
|
|
4.4.0.1 Ejemplo
Si realizamos el experimento aleatorio de lanzar un dado al aire, tenemos:

4.6 Operaciones básicas con sucesos aleatorios
Al ser los sucesos aleatorios nada más que subconjuntos de un conjunto E --espacio muestral--, podemos aplicarles las conocidas operaciones con conjuntos, como son la unión, intersección y diferencia:
4.6.0.0.0.1 Unión:
Dados dos sucesos aleatorios ![]()
, se denomina suceso unión de A y B al conjunto formado por todos los sucesos elementales que pertenecen a A o bien que pertenecen a B (incluyendo los que están en ambos simultáneamente), es decir
![]()
Como ejemplo, tenemos que la unión de un suceso cualquiera con su complementario es el suceso seguro:

Volviendo al ejemplo del lanzamiento de un dado, si ![]()
y ![]()
, el suceso unión de A y B es:

4.6.0.0.0.2 Intersección:
Dados dos sucesos aleatorios ![]()
, se denomina suceso intersección de A y B al conjunto formado por todos los sucesos elementales que pertenecen a A y B a la vez, es decir,
![]()
A veces por comodidad se omite el símbolo ![]()
para denotar la intersección de conjuntos, sobre todo cuando el número de conjuntos que intervienen en la expresión es grande. En particular podremos usar la siguiente notación como equivalente a la intersección:
![]()
Un ejemplo de intersección es la de un suceso aleatorio cualquiera, ![]()
, con su complementario, ![]()
, que es el suceso imposible:

Volviendo al ejemplo del dado,

4.6.0.0.0.3 Diferencia:
Dados dos sucesos aleatorios ![]()
, se llama suceso diferencia de A y B, y se representa mediante ![]()
, o bien A-B, al suceso aleatorio formado por todos los sucesos elementales que pertenecen a A, pero no a B:
![]()

Obsérvese que el suceso contrario de un suceso A, puede escribirse como la diferencia del suceso seguro menos éste, o sea,

4.6.0.0.0.4 Diferencia simétrica:
Si ![]()
, se denomina suceso diferencia simétrica de A y B, y se representa mediante ![]()
, al suceso aleatorio formado por todos los sucesos elementales que pertenecen a A y no a B, y los que están en By no en A:
![]()
Así:

| Figura: Dados dos sucesos aleatorios |
|
|
Hay ciertas propiedades que relacionan la unión, intersección y suceso contrario, que son conocidas bajo el nombre de Leyes de Morgan:

4.8 Experimentos aleatorios y probabilidad
Se denominan experimentos deterministas aquellos que realizados de una misma forma y con las mismas condiciones iniciales, ofrecen siempre el mismo resultado. Como ejemplo, tenemos que un objeto de cualquier masa partiendo de un estado inicial de reposo, y dejado caer al vacío desde una torre, llega siempre al suelo con la misma velocidad: ![]()
4.1
Cuando en un experimento no se puede predecir el resultado final, hablamos de experimento aleatorio. Este es el caso cuando lanzamos un dado y observamos su resultado.
En los experimentos aleatorios se observa que cuando el número de experimentos aumenta, las frecuencias relativas con las que ocurre cierto suceso e, fn(e),
![]()
tiende a converger hacia cierta cantidad que denominamos probabilidad de e.
![]()
4.8.0.1 Ejemplo
En la Figura 4.3 se presenta la evolución de la frecuencia relativa del número de caras obtenido en el lanzamiento de una moneda en 100 ocasiones (simulado por un ordenador). En principio la evolución de las frecuencias relativas es errática, pero a medida que el número de tiradas aumenta, tiende a lo que entendemos por probabilidad de cara.
| Figura: Convergencia a 1/2 de la frecuencia relativa del número de caras obtenido en lanzamientos sucesivos de una moneda (simulación en ordenador). |
|
|
Esta es la noción frecuentista de probabilidad. Sin embargo esta definición no se puede utilizar en la práctica pues:
-
se requiere realizar un número infinito de veces un experimento para calcular una probabilidad. Por ejemplo, lanzar infinitas veces un dado para ver que las frecuencias relativas de la aparición de cada cara convergen a 1/6. Esto puede suplirse en la práctica realizando el experimento un número suficientemente elevado de veces, hasta que tengamos la precisión que requieran nuestros cálculos. Sin embargo,
-
los experimentos aleatorios a veces no pueden ser realizados, como es el caso de calcular la probabilidad de morir jugando a la ruleta rusa con un revolver: no es posible (o no se debe) calcular esta probabilidad repitiendo el experimento un número indefinidamente alto de veces para aproximarla mediante la frecuencia relativa). Para ello existen métodos mucho más seguros, como los que mencionaremos a continuación.
4.8.4 Definición axiomática de probabilidad
Para hacer una definición rigurosa de la probabilidad, necesitamos precisar ciertas leyes o axiomas que deba cumplir una función de probabilidad. Intuitivamente estos axiomas deberían implicar, entre otras, las siguientes cuestiones, que nos parecen lógicas en términos de lo que se puede esperar de una función de probabilidad:
-
La probabilidad sólo puede tomar valores comprendidos entre 0 y 1(no puede haber sucesos cuya probabilidad de ocurrir sea del

ni del
; -
La probabilidad del suceso seguro es 1, es decir, el

; -
La probabilidad del suceso imposible debe ser 0.
-
La probabilidad de la intersección de dos sucesos debe ser menor o igual que la probabilidad de cada uno de los sucesos por separado, es decir,
![]()
![]()
-
La probabilidad de la unión de sucesos debe ser mayor que la de cada uno de los sucesos por separado:
![]()
![]()
Más aún, si los sucesos son disjuntos (incompatibles) debe ocurrir que
![]()
-
La probabilidad del suceso contrario de A, debe valer

. Esto en realidad puede deducirse del siguiente razonamiento:
![]()
En las últimas líneas hemos esbozado ciertas propiedades que debería cumplir una función que queramos llamar probabilidad. Hemos de tener en cuenta entonces que siguiendo esos puntos:
1.
La función de probabilidad debe calcularse sobre subconjuntos de E. No es estrictamente necesario que sean todos, pero si es necesario que si se puede calcular sobre un conjunto, lo pueda ser también sobre su complementario, y que si se puede calcular sobre dos conjuntos A y B, que también se pueda calcular sobre su unión y su intersección. Para ello introduciremos el concepto de ![]()
-álgebra de sucesos, que será una clase de subconjuntos de Esobre los que podamos aplicar las reglas de la probabilidad.
2.
Entre las leyes que debe cumplir una función de probabilidad y que hemos escrito antes, hemos observado que algunas son redundantes, ya que se pueden deducir de las demás. Con la definición axiomática de la probabilidad pretendemos dar el menor conjunto posible de estas reglas, para que las demás se deduzcan como una simple consecuencia de ellas.
Precisemos entonces los conceptos de ![]()
-álgebra de sucesos y de probabilidad.
4.8.4.1 Concepto de ![]()
-álgebra de sucesos
Sea ![]()
una clase no vacía formada por ciertos subconjuntos del espacio muestral E. Diremos que esta clase es un ![]()
-álgebra de sucesos si los sucesos complementarios de aquellos que están en ![]()
también están en ![]()
, así como sus uniones numerables (sean finitas o infinitas). Esto se puede enunciar como:

4.8.4.2 Concepto axiomático de probabilidad
Dado un espacio muestral E, y un ![]()
-álgebra de sucesos ![]()
sobre él, diremos que ![]()
es una probabilidad sobre ![]()
si las siguientes propiedades (axiomas) son verificadas:
Ax-1.
La probabilidad es una función definida sobre ![]()
y que sólo toma valores positivos comprendidos entre 0 y 1

Ax-2.
La probabilidad del suceso seguro es 1
![]()
Ax-3.
La probabilidad de la unión numerable de sucesos disjuntos es la suma de sus probabilidades (figura 4.4):

| Figura: El tercer axioma de probabilidad indica que si |
|
|
4.8.4.3 Observación
La introducción de la definición de ![]()
-álgebra puede parecer innecesaria a primera vista, ya que es una clase formada por subconjuntos de Eque verifican ciertas propiedades relativas a la complementariedad y a las uniones finitas que ya verifica de antemano el conjunto denominado partes de E, P(E), formado por todos los subconjuntos de E. Cuando el conjunto E de los posibles resultados de un experimento aleatorio sea finito, normalmente consideraremos como ![]()
-álgebra de sucesos al conjunto P(E). Esto ocurre cuando por ejemplo realizamos el experimento aleatorio de lanzar un dado:
![]()
![]()
Cuando E es infinito no numerable, la estructura del conjunto P(E) puede presentar propiedades extremadamente engorrosas. Entonces es más conveniente utilizar como ![]()
-álgebra un subconjunto más pequeño suyo, pero no tanto que no nos permita realizar las operaciones de complementariedad o de uniones finitas que se precisan en la definición de un ![]()
-álgebra. Por ejemplo, si realizamos el experimento aleatorio de esperar el tiempo que hace falta para que un átomo de carbono catorce, C14, se desintegre de modo natural, se tiene que
![]()
sin embargo, el ![]()
-álgebra de sucesos que consideramos no es ![]()
, que es una clase demasiado compleja para definir sobre sus elementos una medida de probabilidad. En su lugar consideramos el ![]()
-álgebra formada por todos los intervalos, abiertos o cerrados, y sus uniones finitas
![]()
lo que por supuesto incluye a los puntos de ![]()
, ya que por ejemplo
![]()
Este tipo de conjuntos (los intervalos) son los que nos interesan en la práctica, v.g. calcular la probabilidad de que el peso en kilogramos de un niño al nacer esté en el intervalo [2,4]. De esto modo vamos a realizar el siguiente convenio a lo largo del libro:
No haremos en general referencia al ![]()
-álgebra de sucesos más que cuando sea estrictamente necesario. De este modo cuando a partir de ahora se diga `` ![]()
'', nos referiremos implícitamente a que ![]()
, donde ![]()
es un ![]()
-álgebra de sucesos asociado a E y sobre el que se ha definido la función de probabilidad.
Si el espacio muestral es finito o infinito numerable, entenderemos que el ![]()
-álgebra de sucesos es por defecto P(E).
Si E es un conjunto infinito no numerable como ![]()
, ![]()
, o subconjuntos suyos en forma de intervalos, entenderemos que el ![]()
-álgebra asociada es la mencionada en el ejemplo anterior, es decir, la formada por todos los intervalos abiertos, cerrados o semi-abiertos (lo que incluye en particular a los puntos), y sus uniones finitas. De este modo podremos calcular probabilidades como las siguientes:
![]()
4.10 Probabilidad condicionada e independencia de sucesos
Sea ![]()
un suceso aleatorio de probabilidad no nula, ![]()
. Para cualquier otro suceso ![]()
, llamamos probabilidad condicionada de A a B a la cantidad que representamos mediante ![]()
o bien ![]()
y que se calcula como:

4.10.0.1 Ejemplo
Se lanza un dado al aire ¿Cuál es la probabilidad de que salga el número 4? Si sabemos que el resultado ha sido un número par, ¿se ha modificado esta probabilidad?
Solución:
El espacio muestral que corresponde a este experimento es
![]()
y se ha de calcular la probabilidad del suceso ![]()
. Si el dado no está trucado, todos los números tienen la misma probabilidad de salir, y siguiendo la definición de probabilidad de Laplace,

Obsérvese que para calcular la probabilidad de A según la definición de Laplace hemos tenido que suponer previamente que todos los elementos del espacio muestral tienen la misma probabilidad de salir, es decir:
![]()
Por otro lado, si ha salido un número par, de nuevo por la definición de probabilidad de Laplace tendríamos

Esta misma probabilidad se podría haber calculado siguiendo la definición de la probabilidad condicionada, ya que si escribimos

y entonces
![]()
que por supuesto coincide con el mismo valor que calculamos usando la definición de probabilidad de Laplace.
4.10.0.2 Observación
Obsérvese que según la definición de probabilidad condicionada, se puede escribir la probabilidad de la intersección de dos sucesos de probabilidad no nula como

O sea, la probabilidad de la intersección de dos sucesos, es la probabilidad de uno cualquiera de ellos, multiplicada por la probabilidad del segundo sabiendo que ha ocurrido el primero.
Si entre dos sucesos no existe ninguna relación cabe esperar que la expresión ``sabiendo que'' no aporte ninguna información. De este modo introducimos el concepto de independencia de dos sucesos A y B como:
![]()
Esta relación puede ser escrita de modo equivalente, cuando dos sucesos son de probabilidad no nula como

4.12 Ciertos teoremas fundamentales del cálculo de probabilidades
Hay algunos resultados importantes del cálculo de probabilidades que son conocidos bajo los nombres de teorema de la probabilidad compuesta, teorema de la probabilidad total y teorema de Bayes. Veamos cuales son estos teoremas, pero previamente vamos a enunciar a modo de recopilación, una serie de resultados elementales cuya demostración se deja como ejercicio para el lector (algunos ya han sido demostrados anteriormente):
4.12.0.1 Proposición
Sean ![]()
no necesariamente disjuntos. Se verifican entonces las siguientes propiedades:
1.
Probabilidad de la unión de sucesos:
![]()
2.
Probabilidad de la intersección de sucesos:

3.
Probabilidad del suceso contrario:
![]()
4.
Probabilidad condicionada del suceso contrario:
![]()
4.12.0.2 Ejemplo
En una universidad el 50% de los alumnos habla inglés, el 20% francés y el 5% los dos idiomas ¿Cuál es la probabilidad de encontrar alumnos que hablen alguna lengua extranjera?
Solución:
Sea A el suceso hablar inglés: ![]()
.
Sea B el suceso hablar francés: ![]()
.
El suceso hablar francés e inglés es ![]()
: ![]()
.
Así:
![]()
4.12.0.3 Ejemplo
En una estación de esquí, para navidad-es, la experiencia indica que hay un tiempo soleado sólo el ![]()
de los días. Por otro lado, se ha calculado que cuando un día es soleado, hay una probabilidad del 20% de que el día posterior también lo sea. Calcular la probabilidad de que, en navidades, un fin de semana completo sea soleado.
Solución: Llamemos S al suceso sábado soleado y D al suceso domingo soleado. La única manera en que un fin de semana completo sea soleado es que lo sea en primer lugar el sábado, y que el domingo posterior también. Es decir:
![]()
Luego sólo el ![]()
de los fines de semana son soleados.
El primero de los teoremas que vamos a enunciar es una generalización de la probabilidad de la intersección de dos sucesos, a la de un número cualquiera pero finito de ellos:
4.12.0.4 Teorema (Probabilidad compuesta)
Sea ![]()
una colección de sucesos aleatorios. Entonces:
![]()
Demostración

Los teoremas que restan nos dicen como calcular las probabilidades de sucesos cuando tenemos que el suceso seguro está descompuesto en una serie de sucesos incompatibles de los que conocemos su probabilidad. Para ello necesitamos introducir un nuevo concepto: Se dice que la colección ![]()
es un sistema exhaustivo y excluyente de sucesos si se verifican las relaciones (véase la figura 4.5):
| Figura: A1,A2,A3,A4 forman un sistema exhaustivo y excluyente se sucesos. |
|
|

![]()
4.12.0.5 Teorema (Probabilidad total)
Sea ![]()
un sistema exhaustivo y excluyente de sucesos. Entonces

Demostración
Obsérvese la Figura 4.6. De ahí realizamos las siguientes operaciones:
| Figura: Si A1,A2,A3,A4 forma un sistema exhaustivo y excluyente se sucesos, podemos calcular la probabilidad de B a partir de las cantidades |
|
|

4.12.0.6 Ejemplo
Se tienen dos urnas, y cada una de ellas contiene un número diferente de bolas blancas y rojas:
-
Primera urna, U1: 3 bolas blancas y 2 rojas;
-
Segunda urna, U2: 4 bolas blancas y 2 rojas.
Se realiza el siguiente experimento aleatorio:
Se tira una moneda al aire y si sale cara se elige una bola de la primera urna, y si sale cruz de la segunda.
¿Cuál es la probabilidad de que salga una bola blanca?
Solución: La situación que tenemos puede ser esquematizada como
|
|
|
|
| U1 |
|
|
|
|
|
|
|
|
|
|
| U2 |
|
|
|
|
|
|
Como U1 y U2 forman un sistema incompatible y excluyente de sucesos (la bola resultado debe provenir de una de esas dos urnas y de una sólo de ellas), el teorema de la probabilidad total nos permite afirmar entonces que
![]()
4.12.0.7 Teorema (Bayes)
Sea ![]()
un sistema exhaustivo y excluyente de sucesos. Sea ![]()
un suceso del que conocemos todas las cantidades ![]()
, ![]()
, a las que denominamos verosimilitudes. entonces se verifica:

Demostración
Es una consecuencia de la definición de probabilidad condicionada en términos de la intersección, y del teorema de la probabilidad total:

4.12.0.8 Ejemplo
Se tienen tres urnas. Cada una de ellas contiene un número diferente de bolas blancas y rojas:
-
Primera urna, U1: 3 bolas blancas y 2 rojas;
-
Segunda urna, U2: 4 bolas blancas y 2 rojas;
-
Tercera urna, U3: 3 bolas rojas.
Se realiza el siguiente experimento aleatorio:
Alguien elije al azar y con la misma probabilidad una de las tres urnas, y saca una bola.
Si el resultado del experimento es que ha salido una bola blanca, ¿cuál es la probabilidad de que provenga de la primera urna? Calcular lo mismo para las otras dos urnas.
Solución:
Vamos a representar en un esquema los datos de que disponemos:
|
|
|
|
| U1 |
|
|
|
|
|
|
|
|
|
|
| U2 |
|
|
|
|
|
|
|
|
|
|
| U3 |
|
|
|
|
|
|
En este caso U1, U2 y U3 forman un sistema incompatible y excluyente de sucesos (la bola resultado debe provenir de una de esas tres urnas y de una sólo de ellas), por tanto es posible aplicar el teorema de Bayes:

Con respecto a las demás urnas hacemos lo mismo:


4.12.0.9 Observación
Obsérvese que en el ejemplo anterior, antes de realizar el experimento aleatorio de extraer una bola para ver su resultado, teníamos que la probabilidad de elegir una urna i cualquiera es ![]()
. Estas probabilidades se denominan probabilidades a priori. Sin embargo, después de realizar el experimento, y observar que el resultado del mismo ha sido la extracción de una bola blanca, las probabilidades de cada urna han cambiado a ![]()
. Estas cantidades se denominan probabilidades a posteriori. Vamos a representar en una tabla la diferencia entre ambas:
| a priori | a posteriori |
|
|
|
|
|
|
|
|
|
| 1 | 1 |
![]()
| Las probabilidades a priori cambian de tal modo de las a posteriori que una vez observado el resultado del experimento aleatorio, se puede afirmar con certeza que no fue elegida la tercera urna. |
Esta fenómeno tiene aplicaciones fundamentales en Ciencia: Cuando se tienen dos teorías científicas diferentes, T1 y T2, que pretenden explicar cierto fenómeno, y a las que asociamos unas probabilidades a priori de ser ciertas,
![]()
podemos llevar a cabo la experimentación que se considere más conveniente, para una vez obtenido el cuerpo de evidencia, B, calcular como se modifican las probabilidades de verosimilitud de cada teoría mediante el teorema de Bayes:
![]()
Así la experimentación puede hacer que una teoría sea descartada si ![]()
o reforzada si ![]()
. Una aplicación básica de esta técnica la tenemos en Medicina para decidir si un paciente padece cierta enfermedad o no, en función de los resultados de un test diagnóstico.
4.16 Problemas
Ejercicio 4..1. Una mujer portadora de hemofilia clásica da a luz tres hijos.
1.
¿Cual es la probabilidad de que de los tres hijos, ninguno esté afectado por la enfermedad?
2.
¿Cual es la probabilidad de que exactamente dos de los tres niños esté afectado?
Ejercicio 4..2. El 60% de los individuos de una población están vacunados contra una cierta enfermedad. Durante una epidemia se sabe que el 20% la ha contraído y que 2 de cada 100 individuos están vacunados y son enfermos. Calcular el porcentaje de vacunados que enferma y el de vacunados entre los que están enfermos..
Ejercicio 4..3. La proporción de alcohólicos que existe en la población de Málaga es, aproximadamente, un 10%; no obstante, en las bajas que dan los médicos de la Seguridad Social difícilmente se encuentra el diagnóstico de alcoholismo. Aparecen sin embargo diagnosticados de hepatopatías, lumbalgias, etc., que pueden hacer sospechar alcoholismo subyacente. Se realizó un estudio que puso de manifiesto que el 85% de los individuos alcohólicos y el 7% de los no alcohólicos sufrían tales patologías. Se desea saber cuál es la probabilidad de que un individuo con esas patologías sea realmente alcohólico.
Ejercicio 4..4. Dos tratamientos A y B curan una determinada enfermedad en el 20% y 30% de los casos, respectivamente. Suponiendo que ambos actúan de modo independiente, cuál de las dos siguientes estrategias utilizaría para curar a un individuo con tal enfermedad:
1.
Aplicar ambos tratamientos a la vez.
2.
Aplicar primero el tratamiento B y, si no surte efecto, aplicar el A.
Ejercicio 4..5. Se eligen al azar 3 deportistas de un equipo de 10 integrantes para realizar un control antidopaje; Se sabe que 2 de los jugadores del equipo han tomado sustancias prohibidas. ¿Cuál es la probabilidad de elegir para el análisis a alguno de los infractores?
Ejercicio 4..6. Estamos interesados en saber cuál de dos análisis A y B es mejor para el diagnóstico de una determinada enfermedad, de la cual sabemos que la presentan un 10% de individuos de la población. El porcentaje de resultados falsos positivos del análisis A es del 15% y el de B es del 22%. El porcentaje de falsos negativos de A es del 7% y de B es del 3%. ¿Cuál es la probabilidad de acertar en el diagnóstico con cada método?
Ejercicio 4..7. Con objeto de diagnosticar la colelitiasis se usan los ultrasonidos. Tal técnica tiene una sensibilidad del 91% y una especificidad del 98%. En la población que nos ocupa la probabilidad de colelitiasis es del 20%.
1.
Si a un individuo de tal población se le aplican los ultrasonidos y dan positivos, ¿cuál es la probabilidad de que sufra la colelitiasis?
2.
Si el resultado fuese negativo, ¿cuál es la probabilidad de que no tenga la enfermedad?
Ejercicio 4..8. Entre los estudiantes de una Facultad de Filosofía y Letras se dan las siguientes proporciones: el 40% son hombres. El 70% de los varones fuman, mientras que entre las mujeres sólo fuman el 20%. Escogido un estudiante al azar, calcúlese la probabilidad de que fume.
Ejercicio 4..9. Los estudios epidemiológicos indican que el 20% de los ancianos sufren un deterioro neuropsicológico. Sabemos que la tomografía axial computerizada (TAC) es capaz de detectar este trastorno en el 80% de los que lo sufren, pero que también da un 3% de falsos positivos entre personas sanas. Si tomamos un anciano al azar y da positivo en el TAC, ¿cuál es la probabilidad de que esté realmente enfermo?
Ejercicio 4..10. Sabemos que tiene estudios superiores el 15% de la población española, estudios medios el 40%, estudios primarios el 35% y no tiene estudios el 10%. Los desempleados no se distribuyen proporcionalmente entre esas categorías, dado que de entre los de estudios superiores están sin trabajo el 10%, entre los de estudios medios el 35%, entre los de estudios primarios el 18%, y entre los que no tienen estudios el 37%. Obtenga las probabilidades de que extraído uno al azar, éste sea:
1.
Titulado superior, sabiendo que está parado.
2.
Un sujeto sin estudios que está en paro.
3.
Un sujeto con estudios primarios o que está trabajando.
Ejercicio 4..11. Una enfermedad puede estar producida por tres virus A, B, y C. En el laboratorio hay 3 tubos de ensayo con el virus A, 2 tubos con el virus B y 5 tubos con el virus C. La probabilidad de que el virus A produzca la enfermedad es de 1/3, que la produzca B es de 2/3 y que la produzca el virus C es de 1/7. Se inocula un virus a un animal y contrae la enfermedad. ¿Cuál es la probabilidad de que el virus que se inocule sea el C?
Ejercicio 4..12. El 70% de los estudiantes aprueba una asignatura A y un 60% aprueba otra asignatura B. Sabemos, además, que un 35% del total aprueba ambas. Elegido un estudiante al azar, calcular las probabilidades de las siguientes situaciones:
1.
Haya aprobado la asignatura B, sabiendo que ha aprobado la A.
2.
Haya aprobado la asignatura B, sabiendo que no no ha aprobado la A.
3.
No haya aprobado la asignatura B, sabiendo que ha aprobado la A.
4.
No haya aprobado la asignatura B, sabiendo que no ha aprobado la A.
Ejercicio 4..13. La cuarta parte de los conductores de coche son mujeres. La probabilidad de que una mujer sufra un accidente en un año es de 5/10.000, y para los hombres es de 1/10.000. Calcúlese la probabilidad de que si acaece un accidente, el accidentado sea hombre.
Ejercicio 4..14. En un campus universitario existen 3 carreras sanitarias. Se sabe que el 50% cursan estudios de Enfermería, el 30% Medicina y el 20% Veterinaria. Los que finalizaron sus estudios son el 20, 10 y 5% respectivamente. Elegido un estudiante al azar, hállese la probabilidad de que haya acabado la carrera.
Descargar
| Enviado por: | Satriani |
| Idioma: | castellano |
| País: | Chile |