Matemáticas
Pitágoras
ÍNDICE
Índice---------------------------------------------------------------------1
Biografía de Pitágoras----------------------------------------------2
Introducción------------------------------------------------------------3
Triangulo rectángulo-------------------------------------------------4
Teorema de Pitágoras------------------------------------------------4
Aplicación del teorema de Pitágoras----------------------------8
Utilidad teorema de Pitágoras------------------------------------10
Biografía de Pitágoras
Pitágoras (c. 582-c. 500 a.C.), filósofo y matemático griego, cuyas doctrinas influyeron mucho en Platón. Nacido en la isla de Samos, Pitágoras fue instruido en las enseñanzas de los primeros filósofos jonios Tales de Mileto, Anaximandro y Anaxímenes. Se dice que Pitágoras había sido condenado a exiliarse de Samos por su aversión a la tiranía de Polícrates. Hacia el 530 a.C. se instaló en Crotona, una colonia griega al sur de Italia, donde fundó un movimiento con propósitos religiosos, políticos y filosóficos, conocido como pitagorismo. La filosofía de Pitágoras se conoce sólo a través de la obra de sus discípulos.
Doctrinas básicas
Los pitagóricos asumieron ciertos misterios, similares en muchos puntos a los enigmas del orfismo. Aconsejaban la obediencia y el silencio, la abstinencia de consumir alimentos, la sencillez en el vestir y en las posesiones, y el hábito del autoanálisis. Los pitagóricos creían en la inmortalidad y en la transmigración del alma. Se dice que el propio Pitágoras proclamaba que él había sido Euphorbus, y combatido durante la guerra de Troya, y que le había sido permitido traer a su vida terrenal la memoria de todas sus existencias previas.
Teoría de los números
Entre las amplias investigaciones matemáticas realizadas por los pitagóricos se encuentran sus estudios de los números pares e impares y de los números primos y de los cuadrados, esenciales en la teoría de los números. Desde este punto de vista aritmético, cultivaron el concepto de número, que llegó a ser para ellos el principio crucial de toda proporción, orden y armonía en el universo. A través de estos estudios, establecieron una base científica para las matemáticas. En geometría el gran descubrimiento de la escuela fue el teorema de la hipotenusa, conocido como teorema de Pitágoras, que establece que el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los otros dos lados.
Astronomía
La astronomía de los pitagóricos marcó un importante avance en el pensamiento científico clásico, ya que fueron los primeros en considerar la tierra como un globo que gira junto a otros planetas alrededor de un fuego central. Explicaron el orden armonioso de todas las cosas como cuerpos moviéndose de acuerdo a un esquema numérico, en una esfera de la realidad sencilla y omnicomprensiva. Como los pitagóricos pensaban que los cuerpos celestes estaban separados unos de otros por intervalos correspondientes a longitudes de cuerdas armónicas, mantenían que el movimiento de las esferas da origen a un sonido musical, la llamada armonía de las esferas.
Introducción:
El conocimiento del teorema de Pitágoras es milenario y no obstante que ha sido demostrado en muchas formas diferentes y de que aparentemente ya se conoce todo con respecto a este teorema, muchas propiedades sorprendentes de la ecuación Pitagórica han permanecido ocultas.
El teorema de Pitágoras es un teorema que se aplica exclusivamente a triángulos rectángulos, y nos sirve para obtener un lado o la hipotenusa de un triángulo, si es que se conocen los otros dos.
El teorema se enuncia así:
c2 = a2+ b2
Hipotenusa = cateto a al cuadrado + cateto b al cuadrado
Donde a y b son los lados del triángulo rectángulo, y c siempre es la hipotenusa (el lado más grande del triángulo).
TRIÁNGULOS RECTÁNGULOS
Los triángulos rectángulos cumplen una serie de relaciones métricas importantes entre sus lados.
Los lados de un triángulo rectángulo que forman el ángulo recto, b y c, se llaman catetos y el tercer lado, a, (opuesto al ángulo recto) es la hipotenusa. El teorema de Pitágoras relaciona los dos catetos y la hipotenusa: en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos:
a2 = b2 + c2
Otra relación importante que se cumple en un triángulo rectángulo es el teorema del cateto: el cuadrado de cada cateto es igual al producto de la hipotenusa por su proyección sobre ella, es decir,
c2 = a · m, b2 = a · n
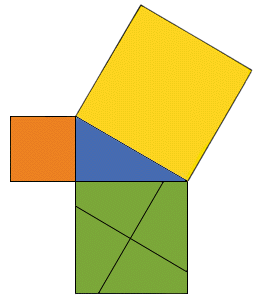
Teorema de Pitágoras
En un triángulo rectángulo, a los lados que forman el ángulo recto se les llama catetos y al opuesto al ángulo recto, hipotenusa.
La altura de un triángulo rectángulo trazada sobre la hipotenusa divide al triángulo en dos triángulos semejantes entre sí y también semejantes al original.
El teorema de Pitágoras señala:
La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Dicho de otra manera: En un triángulo rectángulo, el área del cuadrado construido sobre la hipotenusa es igual a la suma de las áreas de los cuadrados construidos sobre cada uno de los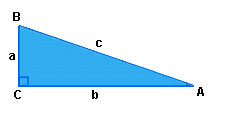
catetos.
Teorema de Pitágoras
El teorema de Pitágoras es un teorema que se aplica exclusivamente a triángulos rectángulos, y nos sirve para obtener un lado o la hipotenusa de un triángulo, si es que se conocen los otros dos. El teorema se enuncia así:
c2 = a2+b2
donde a y b son los lados del triángulo rectángulo, y c siempre es la hipotenusa (el lado más grande del triángulo).
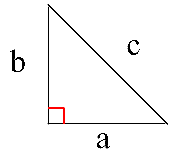
el cuadrito rojo en la esquina del triángulo indica solamente que ese ángulo es recto (o sea, mide exactamente 90°)
Para usar el teorema de Pitágoras, sólo hay que sustituir los datos que te dan, por ejemplo, en el triángulo rectángulo:
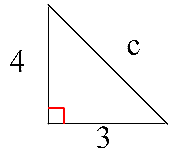
te dan a (que es 3) y b (que es 4), así que sustituimos en la fórmula, y eso nos dá:
c2 = (3)2 + (4)2
elevando al cuadrado, eso da:
c2 = 9 +16 = 25
para obtener el valor de c, sacamos raíz cuadrada:
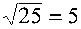
o sea que c = 5.
Cuando lo que te falta es uno de los catetos (uno de los lados, pues) , hay que despejar de la fórmula la a2 o la b2, la que quieras.
así por ejemplo, en el triángulo:
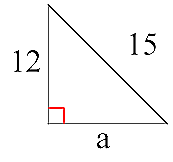
hay que despejar la a de la fórmula del teorema de Pitágoras, la b2 está sumando, la paso restando:
c2- b2 = a2
luego, como es, una igualdad, puedo escribirla así:
a2 = c2 - b2
y ya está despejada.
sustituimos ahora los valores que nos dan de c y b ( 15 y 12)
a2 = (15)2 - (12)2
elevamos al cuadrado y queda:
a2 = 225 - 144 = 81
finalmente, sacamos raíz al resultado, y ese será el valor de a:
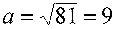
Demostración mediante el cálculo de áreas
La primera demostración se basa en el hecho de que dos cuadrados cuyos lados tienen la misma longitud deben tener la misma área. 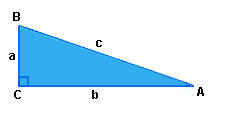
También se usa el cálculo del área de una figura mediante la suma de las áreas de las partes en que se divide dicha figura.
El triángulo ABC es rectángulo.
El ![]()
C = 90°, a y b son los catetos, c es la hipotenusa.
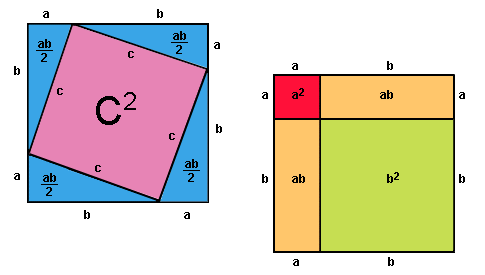
Se construyen dos cuadrados de lado a + b y se divide esta longitud en segmentos de longitudes a y b, como se muestra en las figuras.
Puesto que los dos cuadrados tienen lados de longitud a + b, los dos tienen la misma área.
![]()
El área del cuadrado que se dividió en cuadrados y rectángulos es:
| A = a 2 + 2ab + b 2 |
Como las áreas son iguales, se tiene 2ab + c2 = a2 + 2ab + b2. Restando 2 ab de ambos miembros de la igualdad se llega a:
| c 2 = a 2 + b 2 |
El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo es igual que la suma de las áreas de los cuadrados construidos sobre los catetos.
Demostración usando longitudes de segmentos
Si en lugar de las áreas se consideran longitudes de segmentos, el teorema de Pitágoras se puede enunciar así: el cuadrado de la longitud de la hipotenusa de un triángulo es igual que la suma de los cuadrados de las longitudes de los catetos.
La altura de un triángulo rectángulo trazada sobre la hipotenusa divide el triángulo en dos triángulos semejantes entre sí, y también semejantes al triángulo original.
En el triángulo rectángulo ABC se tiene:
El ![]()
C = 90°, c es la hipotenusa, a y b son los catetos, ![]()
es la altura sobre la hipotenusa.

Para facilitar el siguiente paso, se dibujan los triángulos semejantes como aparecen en la figura anterior.

Aplicando la propiedad fundamental a las proporciones anteriores, se obtiene:
![]()
Sumando las dos igualdades, miembro a miembro, se tiene que:
![]()
Factorizando c en el segundo miembro, resulta:

Demostración geométrica mediante superposición de figuras
1. Se traza un triángulo rectángulo ABC en el que 
C sea igual a 90°, a y b son los catetos, c es la hipotenusa.
2. Ahora se trazan los cuadrados cuyos lados tienen longitudes a, b y c de manera respectiva.
3. Se tratará de probar, mediante superposición, que la suma de las áreas de los cuadrados construidos sobre los catetos es igual que el área del cuadrado construido sobre la hipotenusa.
Para lo cual se requiere:
4. Localizar el punto medio M del cuadrado de longitud b, lo que se logra trazando las diagonales de dicho cuadrado.
5. Por el punto M, se trazan rectas paralelas a los lados del cuadrado construido sobre la hipotenusa 
.
6. Se recorta el cuadrado cuyo lado es a y las partes del cuadrado cuyo lado es b.
7. Se colocan las figuras recortadas sobre el cuadrado cuyo lado es c, como se indica en la figura.
8. Si se cubre exactamente el cuadrado, se cumple que:
c2 = a2 + b2
Utilidad del teorema de Pitágoras
El teorema de Pitágoras es de mucha utilidad en la resolución de problemas de la vida cotidiana.
Por ejemplo:
-
El famoso Galileo Galilei, utilizó el teorema de Pitágoras para determinar la medida de algunas montañas lunares.
-
Conocer la altura de un edificio, sabiendo la medida de la sombra que proyecta y la distancia del punto más alto del edificio al extremo de la sombra.
-
Se desean bajar frutos de un árbol de naranjas, para ello se quiere construir una escalera que sea capaz de alcanzarlos, sabiendo la altura a la que se encuentran los frutos y la distancia del árbol a la base de la escalera.
En general, el Teorema de Pitágoras se puede utilizar para hallar longitudes en donde intervienen triángulos rectángulos.
Actividad Interactiva
Mueva los puntos rojos y responda las siguientes preguntas basándose en la figura que se muestra en el campo de trabajo.
El punto "B" le sirve para manipular la altura del edificio, mientras que el punto "A" le sirve para manipular la dirección del rayo solar.
1. ¿Cuál es altura del edificio, cuando la sombra que proyecta es de 120 metros?
2. Si el edificio tiene una altura de 72 metros y |AB| = 112.468 metros, ¿cuántos metros mide la sombra del edificio?
3. Si la distacia |AB|=104.657 metros y la sombra mide 80.4 metros, ¿cuánto mide la altura del edificio? 4. Si la sombra mide 52 metros y |AB|=103.942 metros, calcule la altura del edificio.
10
Descargar
| Enviado por: | Ruth |
| Idioma: | castellano |
| País: | México |
