Física
Palancas

Universidad de Antofagasta
Facultad de Ciencias Básicas
Departamento de Física
Asignatura: Biofísica
Carrera: Medicina
INDICE
INTRODUCCIÓN
El uso de máquinas simples en muchas de las actividades que se desarrollan a diario es un hecho tan común que su aplicación y utilización en el funcionamiento de determinados dispositivos no nos causa mayor sorpresa. Sin embargo, basta con pensar en la diversidad de aplicaciones que presenta el funcionamiento de nuestro propio organismo para descubrir lo importante que es conocer tales principios y ampliar el rol que cumple la física en este y otros campos de la ciencia y la tecnología.
Previo de iniciar el estudio de palancas y sus aplicaciones, debemos revisar algunos conceptos físicos.
MAQUINAS SIMPLES:
Las máquinas son dispositivos que multiplican una fuerza o bien cambian la dirección de una fuerza, entre las máquinas simples podemos citar a las palancas, las poleas, gatas hidráulicas, tornos, planos inclinados.
Estas máquinas simples nos proporcionan una “ventaja mecánica”. Si se llama Fa a la fuerza de entrada (esfuerzo) que es la que se aplica a la palanca para mantener o levantar una carga y FL a la fuerza de salida o fuerza de carga o resistente), entonces la ventaja mecánica ideal (no se considera perdida por roce) viene dada por: VENTAJA MECANICA = V.M = ![]()
LA PALANCA
La palanca es una máquina simple bastante eficiente. Básicamente está formada por una barra rígida que se puede hacer rotar respecto de un punto línea que recibe el nombre de FULCRO.
Según las posiciones que tengan las dos fuerzas y el fulcro, se definen tres clases de palancas:
Primera clase: el fulcro se encuentra entre ambas fuerzas
Segunda clase: la carga está entre el fulcro y el esfuerzo.
Tercera clase: el esfuerzo está entre el fulcro y la carga.
En el conjunto de figuras siguiente están esquematizadas los tipos de palancas:
I clase II Clase III Clase
OBJETIVOS:
-
Lograr el equilibrio de objetos que pueden rotar en torno a un eje, por medio de la aplicación de momentos.
MATERIALES:
-
Barra graduada
-
Caja de pesas
-
Soporte universal
-
Prensa
-
Dinamómetro
-
Cinta adhesiva
-
Software Data Studio.
-
Hilo
Figura 1
PROCEDIMIENTOS
Experiencia 1:
Montamos un sistema de palanca clase I, mediante el soporte universal y una barra graduada.
Establecemos el equilibrio de la barra con ayuda de una pesa de 5gr.
En uno de los extremos, con la ayuda de las pesas e hilos, establecemos la carga (Fl=mg) de 50gr., que será nuestro valor fijo a una distancia de 49cm (Xl) del eje de rotación de la barra.
En el otro extremo se va a aplicar una fuerza (Fa) a través de un peso(con la ayuda del hilo), que va tener una masa inicial de 50gr., a una distancia del eje de rotación, que va a estar en función de un alcance de equilibrio de la barra, es decir, hasta alcanzar una posición horizontal. Luego esta masa del peso (Fa) va ir aumentando de 5 en 5 hasta obtener 10 valores.
Figura 2
DATOS
| Fa (N) | Fl (N) 0.49 Xl (m) 0.49 | Xa (m) | V.M. | 1 / Xa (m-1) |
| 0.490 | 0.490 | 1.000 | 2.04 | |
| 0.539 | 0.447 | 0.912 | 2.23 | |
| 0.588 | 0.407 | 0.830 | 2.45 | |
| 0.637 | 0.377 | 0.769 | 2.65 | |
| 0.686 | 0.348 | 0.710 | 2.87 | |
| 0.735 | 0.326 | 0.665 | 3.06 | |
| 0.784 | 0.307 | 0.626 | 3.25 | |
| 0.833 | 0.289 | 0.589 | 3.46 | |
| 0.882 | 0.272 | 0.555 | 3.67 | |
| 0.931 | 0.258 | 0.526 | 3.87 |
CÁLCULOS
1.- Lo primero es obtener la fuerza a partir de la masa, simplemente se hace la conversión de gr. a Kg. Y luego se multiplica por “g”.
50 gr. 50 gr. " 9,8 m / s2 0,49 N
1000 gr.
2.- Otro cálculo realizado fue la determinación de la ventaja mecánica, que se obtiene por el cuociente entre la distancia de la fuerza aplicada al eje de rotación, y la distancia entre la fuerza de carga al eje de rotación.
V.M = Xa = 0,447 m = 0,912
X1 0,490 m
Nota: También podemos calcular V.M de la siguiente forma:
V.M = F1 = 0.490 = 0,91
Fa 0,539
3.- Se hace necesario también calcular el valor reciproco de Xa, para poder realizar un gráfico lineal de las distintas fuerzas aplicadas versus las distancias a la q se encuentran del eje de rotación.
Reciproco de Xa 1/Xa (m-1) 1/0,447m = 2,23 m-1
GRÁFICOS
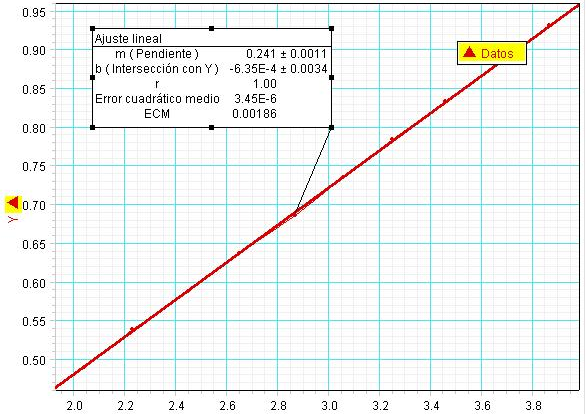
Al graficar la fuerza Aplicada (Fa) versus distancia 1 / Xa (m-1) nos queda:
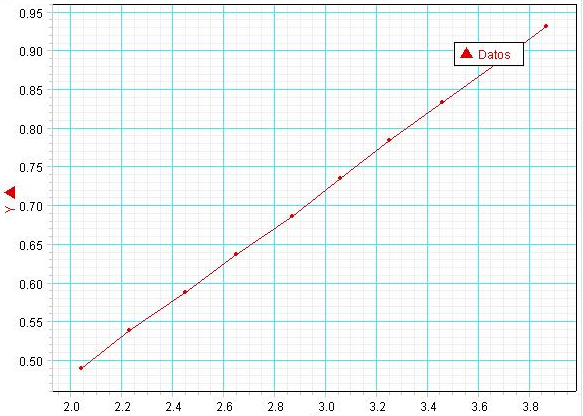
Y al aplicarle una rectificación lineal (línea roja gruesa) nos da R= 1 lo que nos indica, que los datos obtenidos experimentalmente están correctos.
Experiencia 2
Montamos un sistema de palanca clase III, mediante el soporte universal y una barra graduada. Y realizamos el 2do y 3er procedimiento de la experiencia anterior.
Luego, en la misma posición de la Fl, colocamos un dinamómetro, y con la ayuda de un hilo y nuestra fuerza lo sostenemos (de la misma manera que se muestra en la figura 3), hasta lograr el equilibrio. Así el dinamómetro nos indicará la Fa en esa distancia, que se necesita para obtener el equilibrio. El dinamómetro nos indica en cm. la Fa , según lo que se estira el resorte. Por lo que debemos transformar esos cm. en N, mediante la conversión indicada por el fabricante que equivale a 3cm. igual a 1 Newton.
Repetimos el procedimiento anterior, disminuyendo cada vez, la distancia Xa en 4 cm., hasta obtener 8 valores de Fa.
Figura 3
DATOS
| Dinamómetro | Distancia | V.M. | Fl = 0.98 N. Xl= 0.49 m. | ||
| Distancia de Elongación (m) | Newton Equivalentes (N) | Xa (m) | 1/Xa (m-1) | ||
| 2.8 | 0.93 | 0.49 | 2.04 | 1.000 | |
| 3.0 | 1.00 | 0.44 | 2.27 | 0.890 | |
| 3.5 | 1.17 | 0.39 | 2.56 | 0.790 | |
| 3.9 | 1.30 | 0.34 | 2.94 | 0.690 | |
| 4.8 | 1.60 | 0.29 | 3.45 | 0.540 | |
| 6.0 | 2.00 | 0.24 | 4.16 | 0.489 | |
| 7.4 | 2.47 | 0.19 | 5.26 | 0.387 | |
| 9.9 | 3.30 | 0.14 | 7.14 | 0.285 | |
CÁLCULOS
1.- Para calcular la fuerza aplicada a partir de la distancia de elongación del resorte del dinamómetro se procede a utilizar la equivalencia especificada por el fabricante, y con una regla de tres simple se calcula la fuerza.
3 cm. 1 N x = 0,93 N
2,8 cm. x
2.- Al igual que la experiencia anterior para graficar el funcionamiento de esta palanca se necesita calcular el inverso o reciproco de la distancia entre la fuerza aplicada y el eje de rotación.
Reciproco de Xa 1/Xa (m-1) 1/0,44m = 2,27 m-1
3.- Para luego poder comparar las eficiencias en los dos tipos de palanca, debemos también calcular la ventaja mecánica de esta palanca, de manera equivalente a la anterior:
V.M = Xa = 0,44 m = 0,89
X1 0,49 m
GRÁFICOS
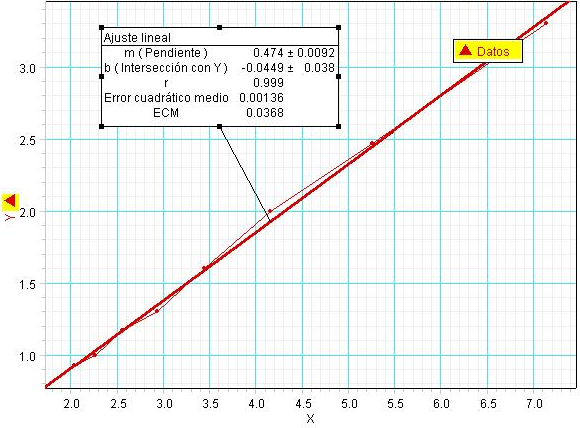
Al graficar la fuerza Aplicada (Fa) versus distancia 1 / Xa (m-1) nos queda:
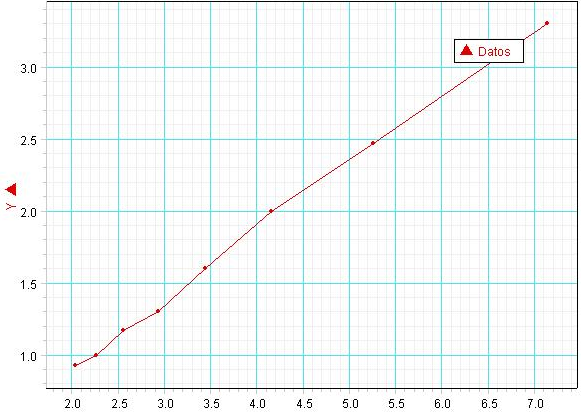
Y al aplicarle una rectificación lineal (línea roja gruesa) nos da R= 0.999 lo que nos indica, que los datos obtenidos experimentalmente están correctos.
CUESTIONARIO
Dinamómetro
Peso Peso
Dinamómetro Figura N°4
a) Identifique clase de palancas:
-
Pinza: Clase III, debido que las fuerzas están dispuestas de la siguiente manera: la fuerza de carga esta ubicada en un extremo, la fuerza aplicada esta entre el pivote (eje giro) y la fuerza de carga.
-
Tenaza: Clase I, ya que la ubicación de sus fuerzas es: la fuerza aplicada en un extremo, la fuerza de carga esta en el otro, encontrándose el pivote (eje giro) en el medio de ambas fuerzas.
-
Remo: Clase I, al igual que en la tenaza las fuerzas se encuentran en los extremos, y el pivote entre ellas.
b) Identifique el tipo de palanca, en cada caso mostrado en la Fig. N°4 ¿Cuál falta? Describa esta última.
En la primera figura encontramos una palanca de clase I, esto se debe a la disposición de las fuerzas en los extremos y el eje de rotación entre estas, en la segunda figura tenemos una palanca de clase III, ya que la fuerza aplicación esta entre la fuerza de carga y el pivote, además su V.M. es menor que uno.
La palanca que no encontramos es la de clase II, esta se produce cuando la fuerza de carga se encuentra entre la fuerza aplicada y el pivote, o sea están en el mismo lado del fulcro, pero la fuerza de carga esta más cerca del pivote y por ende la fuerza aplicada mas al extremo.
c) ¿Qué tipo de palanca es mas eficiente?
Si utilizamos las mismas medidas para XL, Xa y mg., tenemos que la de clase I y III son iguales, por la formula V.M.= FL/Fa, pero también si consideramos todos los datos podemos decir que la clase I es mas ventajosa ya que la ventaja mecánica es igual o menor que uno, y la ventaja mecánica de la clase III es menor a uno (esto es considerando solo las palancas utilizadas en los experimentos)
Si consideramos los tres tipos de palancas la clase II es la mas ventajosa ya que la fuerza aplicada siempre será menor que la fuerza de carga, esto se debe a que el trabajo de las fuerzas es proporcional a la distancias de estas respecto al eje, así en la clase II la fuerza aplicada esta mas lejos del eje que la fuerza de carga, entonces la V.M. será siempre mayor que uno.
d) ¿Qué representa la pendiente de los gráficos rectificados?
Representa el trabajo que se debe aplicar a la barra para lograr el equilibrio (momento de torsión de dichas fuerzas)
e) Explique por que la V.M. de la palanca clase III es menor que uno, y que la palanca de clase II es siempre mayor que uno. Suponga en ambos casos que las fuerzas son perpendiculares a la palanca.
Si tenemos como condición que las fuerzas son perpendiculares a la palanca, tenemos que la V.M. es la razón entre la distancia de la fuerza aplicada y la distancia de la fuerza de carga con respecto al pivote (eje de rotación). Xa/XL=V.M.
Entonces, en la palanca clase II la fuerza aplicada se encuentra a una distancia mayor que la fuerza de carga, dando como resultado mayor que uno.
Y en el caso de la palanca clase III la fuerza aplicada esta a una menor distancia que la fuerza de carga, así la V.M. será menor que uno.
f) Explique como determinaría la masa mL de una carga desconocida utilizando una de las clases de palanca y determine la ecuación correspondiente.
Elegiríamos la palanca clase I, y si tenemos un peso (masa) conocido, que en este caso actuarían como las fuerzas, y también una distancia conocida podremos conocer mL a través de lo siguiente:
WL(mL*g)= peso conocido; XL= distancia conocida; Xa= distancia medida.
mL*g = Xa ; si simplificamos los g mL = Xa
ma*g XL ma XL
mL = Xa * ma
XL
Entonces medimos la distancia entre Xa y el pivote y con los otros dos datos conocidos, remplazamos y obtenemos la mL.
FUENTES DE ERROR
Los siguientes eventos pueden ocasionar un error despreciable en la determinación de las magnitudes estudiadas:
La barra graduada usada como palanca podría estar no totalmente equilibrada, ya que para esto se utiliza una percepción subjetiva.
Al usar dinamómetro la medida realizada en el puede haber tenido una leve error debido a que el resorte al momento de medir con la regla se esta moviendo.
Al ubicar la carga a la distancia que se requiere, puede haber un error en la determinación de esa distancia.
CONCLUSIÓN
De este trabajo experimental podemos concluir que la palanca es un tipo de maquina simple que se caracteriza por disminuir la fuerza a ejercer para levantar cargas pesadas y esto fue comprobado con las dos experiencias realizadas.
En ambas se observo que a mayor distancia del eje de giro, la fuerza es capaz de levantar una mayor carga, lo que se ve también reflejado en el aumento de la ventaja mecánica.
Sin embargo en el experimento realizado el aumento esta ventaja mecánica no fue de un valor tan considerable por lo que podemos decir que como palancas, el sistema armado no es tan eficiente.
A través de la identificación de las fuerzas de carga y aplicadas en diversos instrumentos se analizaron los tres principales tipos de palanca que son:
Primera clase: el fulcro se encuentra entre ambas fuerzas
Segunda clase: la carga está entre el fulcro y el esfuerzo.
Tercera clase: el esfuerzo está entre el fulcro y la carga.
De las anteriores la mas eficiente es la clase II, ya que la fuerza aplicada siempre será menor que la fuerza de carga, esto se debe a que el trabajo de las fuerzas es proporcional a la distancias de estas respecto al eje, así en la clase II la fuerza aplicada esta mas lejos del eje que la fuerza de carga, entonces la V.M será siempre mayor que uno.
2
Fl
xa
xL
Fa
FL
Fl
Fl
Xa
Fa
Fa
Fa
FULCRO
Fl = 0.98N ( 100gr)
Dinamómetro (Fa)
M
Xl
?
0,49 m yfghfLL
?
Valor fijo = 50 gr.
Descargar
| Enviado por: | Csar |
| Idioma: | castellano |
| País: | Chile |
