Física
Ondas
ONDAS
4.1.- Establecer cuál de las siguientes funciones tiene forma y = f(x - vt) o y = f(x + vt). ¿Podría usarse alguna de estas funciones para representar una onda viajera en una cuerda? Comprobar que dichas funciones cumplen la ecuación de onda.
Para que una función pueda representar una onda viajera en una cuerda, tiene que ser una función de dicha forma. La ecuación de onda es: ![]()
(a) ![]()
.
Esta función ya está escrita en dicha forma, y por tanto podría representar una onda viajera en una cuerda, que se mueve hacia la izquierda.
Veamos si verifica la ecuación de ondas:
![]()
![]()
Vemos que efectivamente verifica la ecuación de ondas.
(b) ![]()
Se puede escribir de la forma y = f(x - vt), por tanto representa una onda que se mueve hacia la derecha en el eje x.
Se comprueba que verifica la ecuación de onda igual que en el ejemplo anterior.
(c) ![]()
Esta expresión no se puede escribir como y = f(x - vt) o y = f(x + vt). Por tanto, no podría representar una onda viajera en una cuerda. Además, se puede comprobar que no cumple la ecuación de ondas.
(d) ![]()
También se puede verificar que esta expresión no se puede escribir de la forma y = f(x - vt) o y = f(x + vt). Por tanto, no podría representar una onda viajera en una cuerda. Además, se puede comprobar que no cumple la ecuación de ondas.
4.2.- Dada la ecuación ![]()
, donde x está en metros y t en segundos, determinar la longitud de onda, la frecuencia, el período, la velocidad de propagación de la onda, la amplitud y el sentido de propagación. Escribir una onda idéntica que se propague en sentido opuesto.
Esta onda es una onda armónica, de la forma 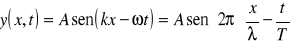
Igualando los términos correspondientes obtenemos:
![]()
![]()
![]()
![]()
![]()
Además, se propaga en el sentido positivo de las x. Una onda idéntica que se propague en sentido opuesto es de la forma:
![]()
4.3.- Un bote en movimiento produce ondas superficiales en un lago tranquilo. El bote realiza 12 oscilaciones de 10 cm de amplitud en 20 segundos, produciéndose en cada oscilación una cresta de onda. Esta creta tarda 6 segundos en alcanzar la orilla del lago distante 12 metros. Escribir la ecuación que describe el movimiento ondulatorio producido y determinar la velocidad a la que se propaga la onda.
Se producen 12 oscilaciones en 20 s. Por tanto, la frecuencia del movimiento es:
![]()
Por tanto, el período del movimiento es
![]()
La amplitud es de 10 cm
![]()
Además, la onda recorre 12 m en 6 s. Por tanto, su velocidad de propagación es:
![]()
La longitud de onda es
![]()
Con estas magnitudes ya podemos escribir la ecuación del movimiento producido:

4.4.- Una onda armónica en una cuerda viene dada por la expresión ![]()
, donde todas las unidades están en el SI. (a) Determinar todas las características de la onda (amplitud, número de onda, frecuencia angular, velocidad, longitud de onda, frecuencia, período y dirección de propagación). (b) Determinar y para el elemento situado en x = 0,22 m en el instante 0,75 s. (c) Determinar las expresiones de la componente y de la velocidad y la aceleración de la cuerda. (d) ¿Cuáles son la velocidad máxima y el valor máximo de la aceleración para cada elemento de la cuerda? (e) Determinar la componente y de la velocidad y la aceleración del elemento situado en x = 0,22 m en el instante t = 0,75 s. ¿Estará la cuerda curvada hacia arriba o hacia abajo en dicho elemento en ese instante?
(a) Comparando la ecuación de la onda con la ecuación de la onda armónica, obtenemos:
![]()
![]()
![]()
![]()
(b) ![]()
(c) La componente y de la velocidad de la cuerda es la primera derivada temporal de y, y la componente y de la aceleración es la segunda derivada temporal:

(d) La velocidad y la aceleración máximas en cada punto se calculan igualando a cero su derivada temporal:


(e) Sólo hay que sustituir los valores de x y t en las ecuaciones obtenidas en el apartado (c):

ay > 0. Por lo tanto, la cuerda está curvada hacia arriba.
4.5.- El rango de frecuencias del sonido audible va desde alrededor de 20 Hz hasta 20 kHz. La velocidad del sonido en el aire es aproximadamente 340 m/s. ¿Cuál es el rango de longitudes de onda del sonido audible en el aire?
Sólo tenemos que emplear la relación entre la velocidad de desplazamiento, la longitud de onda y la frecuencia: ![]()

![]()
4.6.- Un trozo de cuerda de longitud 5.5 m tiene una masa de 0.34 kg. Si la tensión de la cuerda es de 77 N, ¿cuál es la velocidad de una onda en la cuerda?
Sabemos que la velocidad de una onda en una cuerda depende de su densidad lineal de masa, ![]()
, y de la tensión a que está sometida la cuerda:

4.7.- La velocidad de una onda en una cuerda de 5 m es 21 m/s cuando la tensión en la cuerda es 92 N. ¿Cuál es la masa de dicha cuerda?
Utilizando la misma expresión del problema anterior:

![]()
4.8.- Un hilo con una masa por unidad de longitud de 0.15 kg está bajo una tensión de 59 N. ¿Cuál es la potencia promedio de una onda de amplitud 42 mm y frecuencia angular de 130 rad/s que se propaga a lo largo del hilo?
La potencia promedio de una onda que se propaga en una cuerda es:
![]()
donde ![]()
y 
. Por tanto, la potencia promedio es:
![]()
4.9.- En un alambre largo de densidad lineal 3·10-2 kg/m manteniendo una tensión de 30 N provocamos una onda armónica transversal de 0,5 cm de amplitud y 150 Hz de frecuencia. Suponiendo que la onda se mueve en el sentido positivo del eje x y en el origen, y(0, 0) = 0,25 cm y v(0, 0) < 0, calcular la ecuación de onda y las ecuaciones de la velocidad y la aceleración de una partícula del alambre que esté situada a 1 m del origen.
La ecuación de una onda armónica que se propaga en el sentido positivo del eje x es:
![]()
donde A es la amplitud, k es el número de onda, ð la frecuencia angular y ð una constante de fase. Además, el número de onda y la frecuencia angular se relacionan con la velocidad de propagación de la onda mediante la expresión ![]()
. Por tanto, en nuestro caso:
![]()
![]()

![]()
Por tanto, la expresión de la onda es:
![]()
La constante de fase la calculamos teniendo en cuenta las condiciones iniciales que nos dan:
![]()
![]()
Teniendo en cuenta la segunda condición, tenemos que escoger ![]()
. Por tanto, la ecuación de la onda es:
![]()
Para calcular las ecuaciones de la velocidad y la aceleración de una partícula del alambre situada a 1 m del origen únicamente tenemos que derivar esta expresión con respecto al tiempo y sustituir x = 1 m:

4.10.- En una cuerda están presentes dos ondas con la misma amplitud, número de onda, frecuencia angular y dirección de propagación. La diferencia de fase entre estas ondas es 0.65 rad, y la amplitud de cada una es de 51 mm. ¿Cuál es la amplitud de la onda resultante?
Sabemos que cuando interfieren dos ondas de la misma amplitud, número de onda, frecuencia angular y dirección de propagación, la onda resultante es una onda armónica con una amplitud diferente, ![]()
, donde δ es la diferencia de fase entre las ondas y A la amplitud de cada una de ellas por separado. Por tanto, en este caso, la amplitud de la onda resultante es:
![]()
4.11.- Dos ondas armónicas de igual frecuencia, ð = 150 Hz, y amplitud, A = 2 cm, viajan a la velocidad de 1 m/s y en sentido positivo del eje x, existiendo entre ellas una diferencia de fase de ð/3. Escribir la ecuación de onda de cada una de ellas, la ecuación de la onda resultante de la interferencia entre las dos y las ecuaciones del movimiento de una partícula que se encuentra a 20 cm del origen sobre el eje x.
![]()
![]()
Las ecuaciones de las dos ondas son:

La ecuación de la onda resultante es: ![]()
, que queda:
![]()
Las ecuaciones de movimiento de una partícula que se encuentra a 20 cm del origen son:

4.12.- Dos ondas que se mueven en la misma dirección y cuyas ecuaciones en el SI son ![]()
y ![]()
al interferir producen ondas estacionarias. Determinar: (a) La ecuación de la onda resultante. (b) La amplitud en los vientres. (c) La distancia entre dos nodos consecutivos.
(a) La ecuación de onda resultante es:
![]()
(b) Los vientres son los puntos de amplitud máxima. Ésta se da cuando ![]()
. En este caso, la amplitud es:
![]()
(c) Los nodos son los puntos en los cuales la amplitud es cero. Se dan cuando ![]()
. La distancia entre dos nodos consecutivos, por tanto, será la mitad de la longitud de onda, ð/2.
![]()
Por tanto, la distancia entre dos nodos consecutivos es:
![]()
4.13.- Un tren se desplaza a la velocidad de 108 km/h. El silbato de la locomotora emite un sonido de 60 Hz de frecuencia. Calcular la longitud de onda y la frecuencia de las ondas sonoras percibidas por un observador fijo situado (a) delante de la locomotora y (b) detrás de la locomotora. Calcular la frecuencia que percibirá un viajero de otro tren que lleva una velocidad de 54 km/h cuando (c) se aproxima al primer tren y (d) se aleja.
(a) Tenemos un caso típico de efecto Doppler. En este caso, el observador permanece parado, mientras que la fuente se acerca a una velocidad de ![]()
. Por tanto, la frecuencia que percibe el observador es más aguda (mayor) que la que realmente emite el silbato, ![]()
donde v es la velocidad de la onda, en este caso, la velocidad del sonido en el aire, que es de 340 m/s. Por tanto, la frecuencia que percibe el observador es:
![]()
(b) En este caso, el tren se aleja, y por tanto el sonido percibido por el observador será más grave (menor frecuencia) que el emitido realmente por el silbato:
![]()
(c) Ahora el observador también se mueve, y por tanto tenemos que tener en cuenta tanto el movimiento del observador como el de la fuente. En este caso el observador se acerca al primer tren con una velocidad ![]()
. La frecuencia percibida por el observador será:

(d) En este caso se alejan, y la frecuencia es menor que la original:

Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | España |
