Física
Números cuánticos
Los cambios descubiertos en la estructura atómica, con otra interpretación en la regla de Madelung.
La regla de Madelung se utiliza para predecir las estructuras electrónicas con el nombre de regla n+l. Han sido descritas reglas similares como el principio de Aufbau, el principio de construcción, la regla de diagonales o el propio Sistema Periódico de los elementos. Son complementarias las reglas de Hund, el diagrama de Moeller, el Principio de exclusión de Pauli, etc.
Aquí esta regla se presenta con algunas modificaciones, destacando otros puntos de vista. Para resaltar su valor, hay que evitar, de momento, las interpretaciones físicas dadas a sus números. Es conveniente sustituir el nombre de un átomo por el de su número, porque su número es el gran protagonista. Posee un lugar único y concreto asociado a un orden de construcción simétrica, con características a las que corresponderá una actitud física.
Su posición puede definirse con dos referencias bidimensionales, como en un juego de cuadrículas perpendiculares y en los casos complejos la regla puede ampliarse modificada hasta necesitar 4 referencias diferentes, como ocurre para el principio de exclusión de Pauli.
Lo importante para comprender sus sorprendentes atribuciones consiste en recordarlas simultáneamente. No son más difíciles que sería el reglamento de un juego. La regla aparentemente consiste en una forma de predicción de la estructura de los átomos. Una estructura que se distribuye entre niveles y subniveles.
El número de niveles es conocido como n y los distintos subniveles con el número l. Aunque también el número l tiene que representar, con otra forma, al número de componentes de los subniveles.
La naturaleza es tan asombrosa a veces, como autora y protagonista de las matemáticas, que convierte esta distribución en un orden de sorprendentes facultades.
Así, una misma suma con distintos niveles y subniveles muestra algunas de esas atribuciones especiales. Las diferentes combinaciones de dos cifras que sumen un mismo número forman un período. Por ejemplo, una suma de 7, con parejas de distintos números n+l, puestos en orden forman un período completo.
Es decir, la suma de 4 +3, 5+2, 6+1 y 7+0 en sucesión creciente de n asegura un orden de atribuciones.
En la práctica, representamos aquí los casos de posibles números n+l, con su orden para ocho periodos.
8 =5+3=6+2=7+1=8+0.
7 =4+3=5+2=6+1=7+0.
6 =4+2=5+1=6+0.
5 =3+2 =4+1=5+0.
4 =3+1=4+0.
3 =2+1=3+0.
2 =2+0.
1 =1+0.
El conjunto de todos los períodos posibles forman a su vez un sistema simétrico. Un sorprendente comportamiento para la fisica teórica. Para introducirnos en sus peculiaridades debemos seguir las observaciones a una descripción geométrica de sus componentes, dispuestas en el cuadro siguiente.
TABLAS 1. REGLA N+L. ORDEN DE LLENADO
| Orden de ___niveles__ (a) =n+l | 1 .......... | 2 .......... | 3 .......... | 4 .......... | 5 .......... | 6 .......... | 7 .......... | 8 .......... |
(b)
| (c) Atomos |
| 8 |
|
|
|
| 14 | 10 | 6 | 2 | 32 | X. 120 |
| 7 |
|
|
| 14 | 10 | 6 | 2 |
| 32 | Ra 88 |
| 6 |
|
|
| 10 | 6 | 2 |
|
| 18 | Ba 56 |
| 5 |
|
| 10 | 6 | 2 |
|
|
| 18 | Sr 38 |
| 4 |
|
| 6 | 2 |
|
|
|
| 8 | Ca 20 |
| 3 |
| 6 | 2 |
|
|
|
|
| 8 | Mg 12 |
| 2 |
| 2 |
|
|
|
|
|
| 2 | Be 4 |
| 1 | 2 |
|
|
|
|
|
|
| 2 | He 2 |
|
| 2 | 8 | 18 | 32 | 32 | 18 | 8 | 2 |
|
| Orden de ___niveles__ (a) =n+l | 1 .......... | 2 .......... | 3 .......... | 4 .......... | 5 .......... | 6 .......... | 7 .......... | 8 .......... |
(b)
| (c) Atomos |
| 8 |
|
|
|
| 14 (17) | 10(18) | 6(19) | 2(20) | 32 | X. 120 |
| 7 |
|
|
| 14(13) | 10(14) | 6(15) | 2(16) |
| 32 | Ra 88 |
| 6 |
|
|
| 10(10) | 6(11) | 2(12) |
|
| 18 | Ba 56 |
| 5 |
|
| 10(7) | 6(8) | 2(9) |
|
|
| 18 | Sr 38 |
| 4 |
|
| 6(5) | 2(6) |
|
|
|
| 8 | Ca 20 |
| 3 |
| 6(3) | 2(4) |
|
|
|
|
| 8 | Mg 12 |
| 2 |
| 2(2) |
|
|
|
|
|
| 2 | Be 4 |
| 1 | 2(1) |
|
|
|
|
|
|
| 2 | He 2 |
|
| 2 | 8 | 18 | 32 | 32 | 18 | 8 | 2 |
|
La línea horizontal superior indica el orden de niveles con número n.
El orden vertical de la columna (a) 1, 2, 3, 4, 5, 6, 7, no es un orden simple, también es la condición de la suma ya indicada, impuesta a cada línea. El primer número n debe ser el mayor para contener al segundo. Así, con el 1, de mínimo número n, el número l tiene que ser el cero.
Como era previsible, ninguna pareja de números repite, es decir son combinaciones exclusivas. Una modificación adoptada en esta regla, consiste en dar una capacidad para el orden de todos los electrones del sistema, por lo tanto, para distinguir a dos polaridades el número l debe doblar su capacidad.
En esta tabla, si el valor l corresponde a 0, 1, 2, 3, sus componentes toman cifras de una doble sucesión de números impares 1, 3, 5, 7= (2l+1) y se convierten en 2(2l+1) = 2, 6, 10 y 14 referidos a su capacidad de electrones. Y los subniveles l que componen el orden vertical debajo de cada nivel n, son sustituidos por el número de sus componentes.
Entre paréntesis figura el orden de la incorporación que debe coincidir con el orden de número y energía fundamental de los átomos.
Algo confuso. ¿no? Resumiendo:
Las líneas horizontales, son de igual suma n y también coinciden con números atómicos sucesivos que separan los llamados períodos.
Si prescindimos de los paréntesis y de significados físicos se ve que el cuadro corresponde a órdenes muy sencillos, aunque sea una versión geométrica de condicionantes físicas. Estas introducen complejidades que a veces llenan de confusión y dejan sin explicación otros aspectos importantes de las relaciones que aquí serán decisivas.
Llamemos orden de llenado de niveles al orden vertical que los incrementa desde 2 a 14.
Llamemos orden de llenado de períodos a la sucesión de las distintas series de líneas horizontales.
Veremos qué mientras el orden de períodos se compone con números atómicos sucesivos de distintos subniveles, el llenado de niveles se produce con subniveles de distintos números sucesivos.
Mientras el orden de los niveles se llena verticalmente con subniveles l crecientes (2, 6, 10, 14), el orden período se muestra compuesto por subniveles l decrecientes (14, 10, 6, 2). Observemos entonces que el subnivel más alto de cada columna es también el primer miembro del período a su derecha, es decir, pertenece a ambas partes de una simetría bidimensional.
Estos números mágicos de la regla nos invitan a investigar esta relación de simetría entre los órdenes de niveles y órdenes de periodo. Dos direcciones cualitativamente extrañas que deben amparar numerosas implicaciones físicas si descubren relaciones ignoradas. Note que el contenido de cada nivel anticipa el orden simétrico del periodo perpendicular implicado, luego cada nivel como sucede en las células contiene toda la información de la construcción del un sistema a su medida.
Por ejemplo, si en el Sistema Solar se observaran estas reglas, cada planeta contendría la informaciónde todo un sistema solar hasta su medida, y por tanto, estándo Júpiter en un mayor nivel contendría en sí mismo la información de la historia de la estructura de todo el sistema solar.
Esto parece imposible porque sería necesario demostrar la existencia en el sistema solar, de los niveles, simetrías y equivalencias que en la regla se exigen. Pero además, la regla se refiere a una estructura cuya simetría parece despreciar relacionarse directamente con la energía, la masa, la distancia, la densidad, las fuerzas, etc. Es decir, la regla parece desentenderse del resto de la física. Sin embargo, trataremos esto después.
Mientras, obsérvese que cada línea de períodos añadidos a las anteriores produce una simetría general en la distribución de electrones acumulados. Es decir: 2, 2-2, 2-8-2, 2-8-8-2, 2-8-18-8-2, 2-8-18-18-8-2, 2-8-18-32-18-8-2, 2-8-18-32-32-18-8-2, electrones. Sus estructuras corresponden a los átomos con el número 2, 4, 12, 20, 38, 56, 88 y 120, conocidos como He, Be, Mg, Ca, Sr, Ba, Ra, y X que son señalados en la columna (b).
La aparente condición fundamental de esta regla es la formación de átomos simétricos para todos sus períodos completos. La regla establece átomos que de hecho están en la realidad. Sin embargo, esta simetría asocia a la formación de los átomos indicados, una equivalencia entre niveles no citada en ninguna ley.
Para no tener que imaginar, sería conveniente antes de proseguir, exigirle a la regla una prueba de su consistencia, sometiéndola a una contrastación con una física real, con medidas como única interpretación.
Advertimos antes que la terminología científica distingue la capacidad de los subniveles 2, 6, 10,14 con las letras 2=s, 6=p, 10=d y 14=f.
En el cuadro siguiente figuran sobre puntos las medidas en angstroms, de los radios atómicos más conocidos por sucesión de su número atómico. Esto permite trasladar el tamaño de la superficie o límites de los átomos como si fuesen medidas visibles.
![]()
Figura 1. Radios atómicos.
Por las medidas obtenidas vemos la formación de grupos de puntos, cifras en orden descendente, con algunas excepciones explicables como sobreposiciones entre simetrías que pueden justificarse por separado. Estos grupos están compuestos por los subniveles que forman las partes de los períodos. Coinciden con los grupos de 2, 8, 8, 18, 18, 32 conjuntos separados. Los subniveles están designados con su capacidad, letra y los dos números atómicos que los limitan. Los paréntesis indican el nivel al que se agregan las subcapas. Este orden coincide con el del Sistema Periódico de los elementos.
La diferencia para su coincidencia con el orden de la regla consiste en tener que contar sus períodos después de 2s. Entonces el orden de agregación sigue con subniveles sucesivamente menores para obtener la simetría general de la regla por períodos de 2, 2, 8, 8, 18, 18, 32... (Vea la columna (b) de la regla y el margen superior de la figura de radios). Así, mientras cada período de la regla se forma con subniveles de distintos niveles en los períodos de la figura se repiten los subniveles s y p del mismo nivel.
Si llamamos pasos a la diferencia entre los radios, de sucesivos números, el promedio de los pasos sobrepasan el doble de su compresión al cambiar de subniveles. (0,279, 0,129, 0,054 y 0,024 , para 2, 6, 10 y 14). (Vea tabla 6 y 7 al final).
Aquí resalta una cuestión difícilmente explicable: los pasos al añadir electrones contraen el radio del átomo. ¿Se imaginan un depósito donde al añadir contenido se hace más pequeño? Algunos radios atómicos reducen su tamaño más de la mitad con el llenado de un solo subnivel. Por ejemplo, sucede al llenar los subniveles del 5 al 10 o del 13 al 18.
De momento, por faltar una explicación satisfactoria, la incorporación de electrones se ha trasladado a una dimensión perpendicular. En física general, se llama angular. No obstante, también es de difícil interpretación que un espacio añadido a una órbita reste espacio al radio salvo admitir que los electrones no necesitan espacio. Pero necesitan una física capaz de sustituir al radio a cambio de energía, masa, carga, etc.
Aún así, esta física tendría que aplicarse sobre niveles con simetría y órbitas con espacio restado de la dimensión general.
De este modo, la regla indica partes comprimidas por los componentes de un nivel, en simetría perpendicular con partes que se extienden a lo largo de la estructura. Con un orden experimental en la tabla de radios y una diferencia con el orden adoptado por el sistema periódico. Esta diferencia, se inicia con la formación del primer octeto 2s y 6p que se afirma en el interior de cada nivel y altera el orden de los períodos sucesivos de la regla. Octetos señalados por Gilbert N. Lewis.
La imposición del octeto parece deberse a una coincidecia con las condiciones que requiere la generación de los períodos. Al parecer, una misma direccion entre pasos similares produce una asociación común.
Dentro de los niveles que componen el Sistema Periódico, esto coincide en el octeto formado por los subniveles 2s y 6p. (Vea esta sucesión entre 2s y 6p. Tabla 7). Así los pasos de 2s cambian sus promedios cuando están aislados en el primero y último nivel. (Vea los pasos de los numeros 1-2 y 87-88 )
Es interesante tener que asumir en este caso que los promedios sustituyen a la uniformidad que requiere los números enteros y sus simetrías, dentro de los átomos.
Ellos son una característica de la mecánica cuántica, la distribución en la física de resonancias y la regla n+l. En este caso se supone que forman grupos de simetría entre límites de resonancia de caja. Es evidentemente necesario romper la superficie para comprobar su interior y solo puede hacerse con la destrucción de su orden. No hay posibilidad de conocerlo directamente.
Antes de continuar es necesario clarificar otra posible confusión. Para obtener el orden correspondiente a los niveles desde la tabla de radios se tienen que apilar los períodos uno encima de otro en la forma que indica la regla. La necesidad de este amontonamiento para construir el orden de los niveles nos indica que la estructura interior del átomo no puede corresponder directamente al orden de los radios de estos periodos. Quedan como importantes testimonios de puntuales referencias.
Prácticamente, a partir del tercer nivel el orden de cada nuevo período comienza por niveles interiores. Si se extrae o se inserta un electrón del nivel 14, este traspasará dos niveles ya intercalados, sin importar la condición de supuestas corazas circulares o esféricas, que otros niveles interponen en el camino. No manifestará huellas de roturas ni astillas que distingan especialmente estas penetraciones. Su período se enlaza normalmente con el final del octeto anterior.
Quizá sería conveniente repasar para seguir a las nuevas preguntas.
La ciencia actual trata de explicar la estructura atómica, mediante la idea de las partículas de DeBroglie y la ecuación de onda de Schrödinger.
Sin embargo a nuestra escala en la naturaleza, no existe la experiencia de esas partículas ondas. Realmente, no sabemos cómo suceden. Lo mismo ocurre con la interpretación de la rotación del electrón. Aunque sus ecuaciones parecen representar rotaciones y direcciones, explicando otro comportamiento de una determinada energía.
Pero, nosotros tenemos el desafío de sustituir el radio perdido con la incorporación de energía, masa y carga.
El problema podría hallarse, en las diferentes formas de expresión, que una misma física dispone. La relatividad de Einstein ha curvado el espacio absorbiéndolo y asociándolo a la condensación de una masa. Para la relatividad, existe una equivalencia entre masa energía y el espacio de curvatura, implícito en el átomo.
El átomo se acepta como la energía electromagnética que conforma la fórmula E = mc2. También los efectos gravitatorios en el átomo son proporcionales a la masa y son inversamente proporcionales al cuadrado de distancia.
Si nosotros exigimos más consecuencias reales para E= mc2, esta debiera contener también una estructura cuántica con la implicación geométrica y simétrica de números enteros. Y ser aplicable igualmente al Sistema Solar. Para esto, tenemos que incorporar en el átomo el concepto de agregación para la gravedad y la desagregación para la fuga con electrones acumulados en niveles corazas y con ionización de electrones.
Hemos visto cómo la naturaleza mantiene determinados juegos matemáticos fundamentales para formar sus estructuras. Debemos suponer que la regla está unida a los elementales números del orden cuántico y también adopta el Principio de Laves de mayor simetría posible.
Por ejemplo, R.B. Woodward (Nobel) y R. Hoffmann, muestran en La Conservación de la Simetría Orbital, la existencia de una geometría de equilibrio que evita las reacciones, por razones geométricas. Necesitamos algunas explicaciones sobre la posición del número de componentes de los subniveles. La doble sucesión impar 2(1, 3, 5, 7)= 2, 6, 10, 14. La agregación de electrones en el átomo estable es igual al orden de agregación de energía fundamental. El no formar un solo periodo lineal indica la rotura de la continuidad lineal. Así, cada subnivel o nivel es una fragmentación de esa continuidad.
Podemos rechazar las siguientes líneas como argumento absurdo si no aceptamos más que lo demostrable y proseguir luego con demostraciones.
Un origen elemental para una simetría sería un punto sobre una línea con adición de pares de puntos alrededor del central, formando series separadas por repulsión, de 1, 3, 5, 7 puntos. Con exigencias de repulsión geométrica, un ejemplo requiere un enfrentamiento para una doble dimensión simétrica, una repetición o reflexión simultánea respecto a otro eje central. Los 2(1, 3, 5, 7), aparecen en una distribución de crecimiento, como en la figura.
-3., -2, -l.,...0....+l, +2, +3,
-2, -l., 0, +l, +2,
-l., 0, +l,
...0...
...0...
-l., 0, +l,
-2, -l., 0, +l, +2,
-3., -2, -l.,...0....+l, +2, +3,
Si 4 nuevos electrones incrementan la capacidad de sucesivos subniveles, en repulsión simétrica, estos se situarán en los extremos de un espacio cuadrado. Estas separaciones también se asocian con la regla de Hund para lugares antiparalelos. Sumando las series sucesivamente se obtiene 2n2 = 2, 8, 18, 32 que indica la capacidad de los distintos niveles atómicos. Si ellos deben asumir un espacio radial desaparecido, deben poseer espacio radial propio que permita el paso de otras partes de construcción.
Los anillos de los planetas grandes demuestran un plano central, entonces estos electrones podrían adaptar una figura esférica con las polaridades como el efecto de Coriolis.
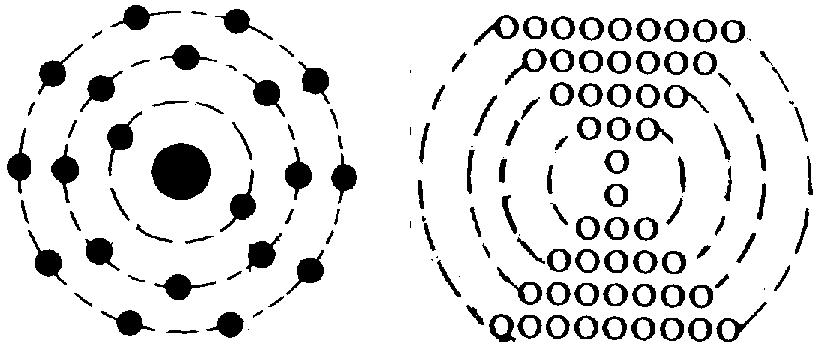
Figura 2.
Añadiendo exigencias, tendrán que adaptarse a la disposición de los números cuánticos. Fig. 3.
.
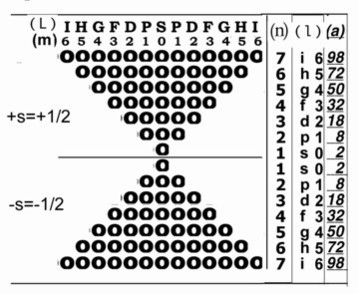
Figura 3. De los números cuánticos.
La adaptación de los números cuánticos se obtiene con 4 números coordinados para pequeños círculos como cuadrículas especiales donde se mide su asimetría. Son designados con las letras n., l, m, y s. Indican el estado de un electrón en orden de energía.
De momento, basta con saber sobre estos números lo siguiente:
(n) La columna n indica entre los extremos de igual número el orden de composición de cada nivel. Estos números normalmente también se indican en con letras mayúsculas. Su orden numérico 1, 2, 3, 4, 5, 6, 7, equivale a K, L, M, N, O, P, Q. Sin embargo las letras mayúsculas se utilizan aquí para la fila L.
(l) La columna l designa los límites de los subniveles con los números o sus letras. Las letras obedecen a un origen histórico. Indica los lugares antiparalelos de Hund en filas opuestas.
(m) Designa el orden de configuración interna o valores de separación magnética de sus componentes.
Considerando la física cuántica, como la mecánica de la alteración de los estados fundamentales de la materia o la energía, no hay indicaciones del estado de la agregación de electrones, sin separación magnética.
(s) Designa las dos polaridades o giros antiparalelos, en este caso, situados en distintos hemisferios, -1/2 y +1/2.
Cuando interviene una acción magnética esos cuatro números nos muestran su estructura escalonada por el desdoblamiento de su energía. Muchos autores utilizan los cuatro números con intervención del campo magnético, con la denominación de n, l, ml y ms.
(a) Indica la capacidad en electrones.
(L) Este orden designa los contenidos de la regla y los lugares de las previsibles transiciones. Indica el orden, de distintos valores implicados, de asimetría angular, en un momento órbital.
No confundir el orden de capacidad, con el orden del llenado sucesivo. Sabemos que el orden de la ocupación simétrica de niveles se invierte en cada periodo al pasar el medio lleno. Para la mayoría de los físicos, los lugares sin ocupar no existen, sin embargo ellos se quedan aquí para mantener el orden que designa las posibles transiciones por alteración. (Próximamente añadiremos un apéndice con la utilidad de esta figura para la representación de transiciones).
Ha llegado el momento de seguir la cuestión importante, dejada atrás, cuando se advirtió una simetría perpendicular extraordinaria y extraña. La propuesta se plantea porque la existencia de un radio para un nivel sería demostrable para otra lógica simple y sorprendente. Sin embargo, este nuevo planteamiento no pretende invocar una mayor lógica, sino llegar a demostraciones prácticas. Los argumentos disponibles hasta ahora no permitían demostraciones.
La regla no puede desentenderse de su repercusión física. Las simetrías por períodos de la regla, el orden de radios atómicos y del Sistema Periódico, no pueden ser espirituales. Tenemos ocasión de efectuar una curiosa prueba:
Distribuir los promedios que corresponden a los componentes de cada nivel. Vea tabla 2. También vea tablas 6 y 7, al final.
Comprobamos que por otra parte las medidas de sus promedios también sugieren la construcción natural de una simetría general para el sistema.
TABLA 2 ORDEN DE LLENADO EN PROMEDIOS DE COMPRESIÓN
| Orden de ___niveles__ (a) =n+l | 1 .......... | 2 .......... | 3 .......... | 4 .......... | 5 .......... | 6 .......... | 7 .......... | 8 .......... |
(b)
| (c)Atomos |
| 8 |
|
|
|
| 0,0242 | 0,0537 | 0,129 | 0,279 | 32 | X. 120 |
| 7 |
|
|
| 0,0242 | 0,0537 | 0,129 | 0,279 |
| 32 | Ra 88 |
| 6 |
|
|
| 0,0537 | 0,129 | 0,279 |
|
| 18 | Ba 56 |
| 5 |
|
| 0,0537 | 0,129 | 0,279 |
|
|
| 18 | Sr 38 |
| 4 |
|
| 0,129 | 0,279 |
|
|
|
| 8 | Ca 20 |
| 3 |
| 0,129 | 0,279 |
|
|
|
|
| 8 | Mg 12 |
| 2 |
| 0,279 |
|
|
|
|
|
| 2 | Be 4 |
| 1 | 0,279 |
|
|
|
|
|
|
| 2 | He 2 |
|
| 2 | 8 | 18 | 32 | 32 | 18 | 8 | 2 |
|
Debe existir una conexión entre la regla y la física todavía sin reconocer.
La ley de Avogadro nos dice que las partículas de los gases tienen la posibilidad de adquirir velocidades y las direcciones infinitas. Pero ellas deben cumplir un promedio fijo de masa, velocidad y espacio por partícula para que en una dimensión macrofísica superior sólo afecte el promedio fijo. Todo lo que se permite a la partícula individual son libertades prestadas a su menor dimensión.
La simetría por tiempo de los péndulos les permite una infinidad, de posiciones instantáneas que inevitablemente tendrán que cumplir un promedio a cuenta de una finalidad superior. La misma incertidumbre no es más que un principio que tiene que someterse a una simetría por tiempo.
No disponemos de otros argumentos. Nosotros sabemos de algunas magnitudes físicas como los valores de radios individuales, como una forma de libertades prestadas, tendrían que ser relacionadas con 2, 8, 18, 32, 18, 8, 2. ¿Qué transformación o síntesis físicas permite equivalencias con números enteros y uniformes para estos componentes?
En una oscilación electromagnética la energía del campo magnético y la energía del campo eléctrico se transforman recíprocamente. Los transformadores se benefician del fenómeno oscilatorio para aplicarlo a números enteros de sus vueltas, con resultados fijos.
Tenemos distintas propiedades asociadas a una unidad de masa, una carga y una energía. Además una capacidad de unirse a otros formando un primer agrupamiento como subnivel y un segundo agrupamiento como nivel. Tenemos una suma de masas para subniveles y niveles. A través de la regla disponemos de un orden sucesivo de construcción.
Las reglas de simetría necesitan la existencia de una forma de equivalencia entre niveles. La equivalencia en la naturaleza no debe ser necesariamente equidistancia, es bastante con una transformación equivalente para una simetría. Para las propiedades de carga existe una simeria entre protones y electrones.
Un sistema solar mostrado separadamente, en velocidades, distancias, masas o energía presentaría propiedades distintas de una sola cosa. Si pueden convertirse en equivalentes, la regla no ve sus diferencias. La simetría de la regla da por supuesto un orden de distancias en equivalencias uniformes. Pero una propiedad que tenga pasos por cuadrados o múltiplos de distancia, no tendría equivalencias en distancias lineales. Sin embargo, sí la propiedad de una velocidad, distancia o tiempo, implica una determinada masa, tendríamos un sistema perfecto, para justificar la estructura de la regla. Y podemos construir una estructura atómica, como un sistema solar elemental.
No obstante, ellas no serían suficientes para predecir nuestro sistema solar. Sin embargo, una distribución regular de la masa en las estrellas puede ser descrita a través la asterosismología. Y, el sistema solar coincide con estructuras y niveles regulares en un modelo que predice las distancias y las velocidades planetarias. Consulte "Sobre la Estructura del Sistema Solar" http://perso.wanadoo.es/30127/
Pero aún faltarían más piezas del rompecabezas, la simetría, entre las masas de las órbitas, o la medida de masas y el radio de los planetas. Nos falta el conocer las equivalencias entre transformaciones. Tampoco sabemos dónde están las cargas.
Parece que hemos terminado.
Pero disponemos de un concepto que aparece en el sistema solar que no aparece en los átomos y otro que aparece en los átomos y no aparece en el sistema solar. Ambos conceptos se refieren a un mismo fenómeno. Recordemos que la desaparición de espacio en radios atómicos, coincidía con la teoría de la relatividad condensando distintas densidades en los espacios electrónicos, que forman los subniveles. Y las diferentes densidades tienen gran importancia para la presencia de las medidas simétricas en la estructura.
Con esto no disponemos de una razón física para la carga pero sí de una razón cualitativa entre unidad de carga-masa y radios independientes. Una mayor compresión de electrones sería una mayor compresión de cargas que estaría relacionada con una proporcional compresión en subniveles y niveles.
El sistema solar no dispone de una asociación entre carga y masa, pero dispone de una distinta compresión, entre sus masas planetarias.
En las primeras ecuaciones de la física atómica se sorprendían los físicos porque los radios del electrón o de una partícula cargada tenían que ser inversamente proporcionales a su masa. Hoy se admite que la masa aumenta con la compresión. Hemos llegado a un punto decisivo de este trabajo. La masa energía tiene que permanecer simétrica con promedio de unidades conocidas de números enteros. Luego, cuando el radio aumente o disminuya tiene que mantener en igual medida la relación m/r.
Este concepto es utilizado como medida en el Sistema Solar, componiendo la velocidad de escape.
La velocidad de escape es menospreciada como concepto fundamental, sin embargo, representa la fuerza antigravedad.
La aceleración sobre una masa unidad tiene la magnitud G(m/r2), dónde m es la masa del cuerpo que atrae, r es la distancia entre los centros de masa.
Velocidad de escape2= 2GM/R o Velocidad de escape = (2G x M/R)1/2
G es la constante de gravitación igual a 6.670 x 10-8 cm2/gram sec2.
Estas relaciones supuestas no pueden probarse directamente en el átomo pero sí podemos hacerlo en el sistema solar advirtiendo su relación con la simetría general. Vea las velocidades de escape correspondientes a los planetas del sistema solar, en la tabla 3. En ellas no se aprecian niveles, ni simetrías.
TABLA 3 . VELOCIDADES DE ESCAPE DE PLANETAS
| Planetas .......... | Distancia Orbita(km) | Radio (km) | (Masa (kg) | Velocidad de escape | Proporción /1,919 | Simetria atómica |
| Mercurio | 57910 | 2439 | 3.30e23 | 4.2 | 2.19 |
|
| Venus | 108200 | 6052 | 4.87e24 | 10.4 | 5,42 |
|
| Tierra | 149600 | 6378 | 5.98e24 | 11.2 | 5,83 |
|
| Marte | 227940 | 3398 | 6.42e23 | 5.0 | 2.6 |
|
| Jupiter | 778000 | 71492 | 1.90e27 | 59.5 | 31 |
|
| Saturno | 1429000 | 60268 | 5.69e26 | 35.5 | 18,49 |
|
| Urano | 2870990 | 25559 | 8.69e25 | 21.3 | 11,1 |
|
| Neptuno | 4504300 | 24764 | 1.02e26 | 23.5 | 12,24 |
|
| Plutón | 5913520 | 1160 | 1.32e22 | 1.3 | 0.68 |
|
Pero veamos lo que ocurre situando sus medidas en el orden de niveles simétricos de caja de resonancia construida sólo, con los argumentos geométricos clásicos del modelo http://perso.wanadoo.es/30127/
Significa la transformación de un espacio esférico, en una caja de resonancia cuadrada. Es la posible equivalencia física de espacios al alejarse de un punto central, obtenida por concentrarse o extenderse en igual proporción.
TABLA 4. VELOCIDADES DE ESCAPE CON SIMETRIAS
| Planetas .......... | Distancia Orbita(km) | Radio (km) | (Masa (kg) | Velocidad de escape | Proporción /1,919 | Simetria atómica |
| Mercurio | 57910 | 2439 | 3.30e23 | 4.2 | 2.19 | 2 |
| Venus/Marte | 291750 | 3099 | 5,51e24 | 15,4 | 8.02 | 8 |
| Tierra/Neptuno | 583500 | 11967 | 1.08e26 | 34.7 | 18,08 | 18 |
| Jupiter | 778000 | 71492 | 1.90e27 | 59.5 | 31 | 32 |
| Saturno | 1429000 | 60268 | 5.69e26 | 35.5 | 18,49 | 18 |
| Urano | 2870990 | 25559 | 8.69e25 | 21.3 | 11,1 | 8 |
| Plutón | 5913520 | 1160 | 1.32e22 | 1.3 | 0.68 | 2 |
La simetría de los niveles, encuentra a dos parejas de planetas que coinciden con su suma en otro lugar. En ese caso, Neptuno y Tierra formaban un planeta anterior, en un lugar de asteroides, convertido el punto central. Recordemos que se atribuye la inclinación de Urano y la órbita de Plutón a los desplazamientos en el origen del sistema.
Tablas complementarias usadas.
Números y radio correspondientes a los períodos de la figura 1.
TABLA 5. RADIOS ELECTRONICOS EN PERIODOS
| 87 2.70 | 88 2.33 |
|
|
|
|
|
|
|
|
|
|
|
| 2s(7) |
| 81 2.08 | 82 1.81 | 83 1.63 | 84 1.53 | 85 1.43 | 86 1.34 |
|
|
|
|
|
|
|
| 6p(6) |
| 71 2.25 | 72 2.16 | 73 2.09 | 74 2.02 | 75 1.97 | 76 1.92 | 77 1.87 | 78 1.83 | 79 1.79 | 80 1.76 |
|
|
|
| 10d(5) |
| 57 2.74 | 58 2.70 | 59 2.67 | 60 2.64 | 61 2.62 | 62 2.59 | 63 2.56 | 64 2.54 | 65 2.51 | 66 2.49 | 67 2.47 | 68 2.45 | 69 2.42 | 70 2.40 | 14f(4) |
| 55 3.34 | 56 2.78 |
|
|
|
|
|
|
|
|
|
|
|
| 2s(6) |
| 49 2.00 | 50 1.72 | 51 1.53 | 52 1.42 | 53 1.32 | 54 1.24 |
|
|
|
|
|
|
|
| 6p(5) |
| 39 2.27 | 40 2.16 | 41 2.08 | 42 2.01 | 43 1.95 | 44 1.89 | 45 1.83 | 46 1.79 | 47 1.75 | 48 1.71 |
|
|
|
| 10d(4) |
| 37 2.98 | 38 2.45 |
|
|
|
|
|
|
|
|
|
|
|
| 2s(5) |
| 31 1.81 | 32 1.52 | 33 1.33 | 34 1.22 | 35 1.12 | 36 1.03 |
|
|
|
|
|
|
|
| 6p(4) |
| 21 2.09 | 22 2.00 | 23 1.92 | 24 1.85 | 25 1.79 | 26 1.77 | 27 1.67 | 28 1.62 | 29 1.57 | 30 1.53 |
|
|
|
| 10d(3) |
| 19 2.77 | 20 2.23 |
|
|
|
|
|
|
|
|
|
|
|
| 2s(4) |
| 13 1.82 | 14 1.46 | 15 1.23 | 16 1.09 | 17 0.97 | 18 0.88 |
|
|
|
|
|
|
|
| 6p(3) |
| 11 2.23 | 12 1.72 |
|
|
|
|
|
|
|
|
|
|
|
| 2s(3) |
| 5 1.17 | 6 0.91 | 7 0.75 | 8 0.65 | 9 0.57 | 10 0.51 |
|
|
|
|
|
|
|
| 6p(2) |
| 3 2.05 | 4 1.40 |
|
|
|
|
|
|
|
|
|
|
|
| 2s(2) |
| 1 0.79 | 2 0.49 |
|
|
|
|
|
|
|
|
|
|
|
| 2s(1) |
TABLA 6. PROMEDIOS DE COMPRESION DE SUBNIVELES
| Números .......... | Subnivel .......... | Orden .......... | Radios .......... | Compresión ............... | Paso .......... | Promedios por paso |
| 1-2 | 2 | (1) | 0,79- 0,49 | 0,30 | /2 | 0,15 |
| 3-4 | 2 | (2) | 2,05 -1,40 | 0,65 | /2 | 0,325 |
| 11-12 | 2 | (4) | 2,23- 1,72 | 0,51 | /2 | 0,255 |
| 19-20 | 2 | (6) | 2,77- 2,23 | 0,54 | /2 | 0,27 |
| 37-38 | 2 | (9) | 2,98 -2,45 | 0,53 | /2 | 0,265 |
| 55-56 | 2 | (12) | 3,34- 2,78 | 0,56 | /2 | 0,28 |
| 87-88 | 2 | (16) | 2,70- 2,33 | 0,37 | /2 | 0,185 |
| Promedio general de 5 con octetos
|
|
|
| 0,558
| /2
| 0,279 .............. |
| Promedio general de 2 sin octetos |
|
|
| 0,335 | /2 | 0,167 |
| 5-10 | 6 | (3) | 1,17- 0,51 | 0,66 | /6 | 0,11 |
| 13-18 | 6 | (5) | 1,82- 0,88 | 0,94 | /6 | 0,157 |
| 31-36 | 6 | (8) | 1,81- 1,03 | 0,78 | /6 | 0,13 |
| 49-54 | 6 | (11) | 2,00- 1,24 | 0,76 | /6 | 0,127 |
| 81-86 | 6 | (15) | 2,08- 1,34 | 0,74 | /6 | 0,123 |
| Promedio general de 6
|
|
|
| 0,776
| /6
| 0,1293 .............. |
| 21-30 | 10 | (7) | 2,09- 1,53 | 0,56 | /10 | 0,056 |
| 39-48 | 10 | (10) | 2,27- 1,71 | 0,56 | /10 | 0,056 |
| 71-80 | 10 | (14) | 2,25- 1,76 | 0,49 | /10 | 0,049 |
| Promedio general de 10
|
|
|
| 0,537
| /10
| 0,0537 ............. |
| 57-70 Promedio general de 14 | 14
| (13)
| 2,74- 2,40
| 0,34
| /14
| 0,0242 ............. |
| Promedio de 2 sin octetos | 0,165 |
| Promedio de 2con octetos | 0,279 |
| Promedio de 6 | 0,129 |
| Promedio de 10 | 0,0537 |
| Promedio de 14 | 0,0242 |
TABLA 7. SIMETRIA SUPUESTA EN NIVELES Y PROMEDIOS
| Números .......... | Nivel
| Subnivel .......... | Orden .......... | Radios .......... | Compresión
| Pasos .......... | PROMEDIOS |
| 87-88 | 7 | 2s | (16) | 2,70- 2,37 | 0,33 | /2 | 0,165 |
|
|
|
|
|
|
|
|
|
| 81-86 | 6 | 6p | (15) | 2,08- 1,30 | 0,776 | /6 | 0,129 |
| 55-56 | 6 | 2s | (12) | 3,34- 2,78 | 0,558 | /2 | 0,279 |
|
|
|
|
|
|
|
|
|
| 71-80 | 5 | 10d | (14) | 2,25 1,71 | 0,537 | /10 | 0,0537 |
| 49-54 | 5 | 6p | (11) | 2,00- 1,22 | 0,776 | /6 | 0,129 |
| 37-38 | 5 | 2s | (9) | 2,98 -2,42 | 0,558 | /2 | 0,279 |
|
|
|
|
|
|
|
|
|
| 57-70 | 4 | 14f | (13) | 2,74- 2,40 | 0,34 | /14 | 0,0242 |
| 39-48 | 4 | 10d | (10) | 2,27- 1,73 | 0,537 | /10 | 0,0537 |
| 31-36 | 4 | 6p | (8) | 1,81- 1,03 | 0,776 | /6 | 0,129 |
| 19-20 | 4 | 2s | (6) | 2,77- 2,21 | 0,558 | /2 | 0,279 |
|
|
|
|
|
|
|
|
|
| 21-30 | 3 | 10d | (7) | 2,09- 1,55 | 0,537 | /10 | 0,0537 |
| 13-18 | 3 | 6p | (5) | 1,66- 0,88 | 0,776 | /6 | 0,129 |
| 11-12 | 3 | 2s | (4) | 2,23- 1,67 | 0,558 | /2 | 0,279 |
|
|
|
|
|
|
|
|
|
| 5-10 | 2 | 6p | (3) | 1,27- 0,51 | 0,776 | /6 | 0,129 |
| 3-4 | 2 | 2s | (2) | 2,05 -1,49 | 0,558 | /2 | 0,279 |
|
|
|
|
|
|
|
|
|
| 1-2 | 1 | 2s | (1) | 0,79- 0,46 | 0,33 | /2 | 0,165 |
Descargar
| Enviado por: | Vikingo |
| Idioma: | gallego |
| País: | México |
